|
SLIP
1.4
|
|
SLIP
1.4
|
This namespace corresponds to the kernel of the Simple Library on Image Processing (SLIP). That is to say that it contains the data structures and the algorithms needed by these data strucutres. More...
Classes | |
| struct | __fill_border |
| struct | __fill_border< std::random_access_iterator_tag > |
| struct | __fill_border< std::random_access_iterator2d_tag > |
| struct | __fill_border< std::random_access_iterator3d_tag > |
| struct | __fill_border< std::random_access_iterator4d_tag > |
| fill border | |
| struct | FillBorder |
| Generic fill border functor: fill border of 1d, 2d or 3d iterator ranges. More... | |
| struct | __update_border |
| struct | __update_border< std::random_access_iterator_tag > |
| struct | __update_border< std::random_access_iterator2d_tag > |
| struct | __update_border< std::random_access_iterator3d_tag > |
| struct | __update_border< std::random_access_iterator4d_tag > |
| update border | |
| struct | UpdateBorder |
| Generic update border functor: update border of 1d, 2d or 3d iterator ranges. More... | |
| struct | __add_border |
| struct | __add_border< std::random_access_iterator_tag > |
| struct | __add_border< std::random_access_iterator2d_tag > |
| struct | __add_border< std::random_access_iterator3d_tag > |
| struct | __add_border< std::random_access_iterator4d_tag > |
| add border | |
| struct | AddBorder |
| Generic add border functor: adds border of 1d, 2d or 3d iterator ranges. More... | |
| struct | RGBtoL |
| Converts a RGB color to a luminance value. More... | |
| struct | RGBtoXYZ |
| Converts a RGB color to XYZ color. More... | |
| struct | XYZtoRGB |
| Converts a XYZ color to RGB color. More... | |
| struct | RGBtoXYZ_v2 |
| Converts a RGB color to XYZ color. Another version (not the same white reference) More... | |
| struct | XYZtoRGB_v2 |
| Converts a XYZ color to RGB color. Another version (not the same white reference) More... | |
| struct | RGBtoYCrCb |
| Converts a RGB color to YCrCb color. More... | |
| struct | YCrCbtoRGB |
| Converts a YCrCb color to RGB color. More... | |
| struct | RGBtoCieLab |
| Converts a RGB color to CieLab color. More... | |
| struct | CieLabtoRGB |
| struct | RGBtoHSV |
| Converts a RGB color to HSV color. More... | |
| struct | HSVtoRGB |
| struct | RGBtoHSI |
| Converts a RGB color to HSI color. More... | |
| struct | HSItoRGB |
| Converts a HSI color to RGB color. More... | |
| struct | RGBtoHSI_01 |
| Converts a RGB color to HSI color. More... | |
| struct | HSItoRGB_01 |
| Converts a HSI color to RGB color. More... | |
| struct | L1_dist |
Computes the L1 distance between two values x and y:  . More... . More... | |
| struct | L2_dist |
Computes the L2 distance between two values x and y: 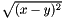 . More... . More... | |
| struct | L22_dist |
Computes the L22 distance between two values x and y: 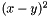 . More... . More... | |
| struct | Relative_error_L1 |
Computes the L1 relative error between two values x and y: 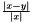 . More... . More... | |
| struct | Relative_error_L2 |
Computes the L2 relative error between two values x and y: 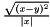 . More... . More... | |
| struct | Relative_error_L22 |
Computes the Relative L22 error between two values x and y: 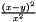 . More... . More... | |
| struct | L1_dist_vect |
Computes the L1 distance between two Vectors x and y: 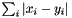 . More... . More... | |
| struct | L2_dist_vect |
Computes the L2 distance between two Vectors x and y: 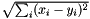 . More... . More... | |
| struct | L22_dist_vect |
Computes the L22 distance between two Vectors x and y: 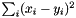 . More... . More... | |
| struct | __copy |
| struct | __copy< std::random_access_iterator_tag > |
| struct | __copy< std::random_access_iterator2d_tag > |
| struct | __copy< std::random_access_iterator3d_tag > |
| struct | __dx |
| struct | __dx< Real, std::random_access_iterator_tag > |
| struct | __dx< Real, std::random_access_iterator2d_tag > |
| struct | __dx< Real, std::random_access_iterator3d_tag > |
| struct | __dx< Real, std::random_access_iterator4d_tag > |
| dx local derivatives 4d extensions | |
| struct | Dx |
| struct | __dy |
| struct | __dy< Real, std::random_access_iterator_tag > |
| struct | __dy< Real, std::random_access_iterator2d_tag > |
| struct | __dy< Real, std::random_access_iterator3d_tag > |
| struct | __dy< Real, std::random_access_iterator4d_tag > |
| dy local derivatives 4d extensions | |
| struct | Dy |
| struct | __dz |
| struct | __dz< Real, std::random_access_iterator_tag > |
| struct | __dz< Real, std::random_access_iterator2d_tag > |
| struct | __dz< Real, std::random_access_iterator3d_tag > |
| struct | __dz< Real, std::random_access_iterator4d_tag > |
| dz local derivatives 4d extensions | |
| struct | Dz |
| struct | __dt |
| dt local derivatives. 4d extensions. | |
| struct | __dt< Real, std::random_access_iterator_tag > |
| struct | __dt< Real, std::random_access_iterator2d_tag > |
| struct | __dt< Real, std::random_access_iterator3d_tag > |
| struct | __dt< Real, std::random_access_iterator4d_tag > |
| struct | Dt |
| struct | __dx_fwd |
| struct | __dx_fwd< Real, std::random_access_iterator_tag > |
| struct | __dx_fwd< Real, std::random_access_iterator2d_tag > |
| struct | __dx_fwd< Real, std::random_access_iterator3d_tag > |
| struct | __dx_fwd< Real, std::random_access_iterator4d_tag > |
| forward dx local derivatives. 4d extensions. | |
| struct | DxFwd |
| struct | __dy_fwd |
| struct | __dy_fwd< Real, std::random_access_iterator_tag > |
| struct | __dy_fwd< Real, std::random_access_iterator2d_tag > |
| struct | __dy_fwd< Real, std::random_access_iterator3d_tag > |
| struct | __dy_fwd< Real, std::random_access_iterator4d_tag > |
| forward dy local derivatives. 4d extensions. | |
| struct | DyFwd |
| struct | __dz_fwd |
| struct | __dz_fwd< Real, std::random_access_iterator_tag > |
| struct | __dz_fwd< Real, std::random_access_iterator2d_tag > |
| struct | __dz_fwd< Real, std::random_access_iterator3d_tag > |
| struct | __dz_fwd< Real, std::random_access_iterator4d_tag > |
| forward dz local derivatives. 4d extensions. | |
| struct | DzFwd |
| struct | __dt_fwd |
| forward dt local derivatives. 4d extensions. | |
| struct | __dt_fwd< Real, std::random_access_iterator_tag > |
| struct | __dt_fwd< Real, std::random_access_iterator2d_tag > |
| struct | __dt_fwd< Real, std::random_access_iterator3d_tag > |
| struct | __dt_fwd< Real, std::random_access_iterator4d_tag > |
| struct | DtFwd |
| struct | __dx_bck |
| struct | __dx_bck< Real, std::random_access_iterator_tag > |
| struct | __dx_bck< Real, std::random_access_iterator2d_tag > |
| struct | __dx_bck< Real, std::random_access_iterator3d_tag > |
| struct | __dx_bck< Real, std::random_access_iterator4d_tag > |
| backward dx local derivatives. 4d extensions. | |
| struct | DxBck |
| struct | __dy_bck |
| struct | __dy_bck< Real, std::random_access_iterator_tag > |
| struct | __dy_bck< Real, std::random_access_iterator2d_tag > |
| struct | __dy_bck< Real, std::random_access_iterator3d_tag > |
| struct | __dy_bck< Real, std::random_access_iterator4d_tag > |
| backward dy local derivatives. 4d extensions. | |
| struct | DyBck |
| struct | __dz_bck |
| struct | __dz_bck< Real, std::random_access_iterator_tag > |
| struct | __dz_bck< Real, std::random_access_iterator2d_tag > |
| struct | __dz_bck< Real, std::random_access_iterator3d_tag > |
| struct | __dz_bck< Real, std::random_access_iterator4d_tag > |
| backward dz local derivatives. 4d extensions. | |
| struct | DzBck |
| struct | __dt_bck |
| backward dt local derivatives. 4d extensions. | |
| struct | __dt_bck< Real, std::random_access_iterator_tag > |
| struct | __dt_bck< Real, std::random_access_iterator2d_tag > |
| struct | __dt_bck< Real, std::random_access_iterator3d_tag > |
| struct | __dt_bck< Real, std::random_access_iterator4d_tag > |
| struct | DtBck |
| struct | __prewittx |
| struct | __prewittx< Real, std::random_access_iterator_tag > |
| struct | __prewittx< Real, std::random_access_iterator2d_tag > |
| struct | __prewittx< Real, std::random_access_iterator3d_tag > |
| struct | Prewittx |
| struct | __prewitty |
| struct | __prewitty< Real, std::random_access_iterator_tag > |
| struct | __prewitty< Real, std::random_access_iterator2d_tag > |
| struct | __prewitty< Real, std::random_access_iterator3d_tag > |
| struct | Prewitty |
| struct | __prewittz |
| struct | __prewittz< Real, std::random_access_iterator_tag > |
| struct | __prewittz< Real, std::random_access_iterator3d_tag > |
| struct | Prewittz |
| struct | __sobelx |
| struct | __sobelx< Real, std::random_access_iterator_tag > |
| struct | __sobelx< Real, std::random_access_iterator2d_tag > |
| struct | __sobelx< Real, std::random_access_iterator3d_tag > |
| struct | Sobelx |
| struct | __sobely |
| struct | __sobely< Real, std::random_access_iterator_tag > |
| struct | __sobely< Real, std::random_access_iterator2d_tag > |
| struct | __sobely< Real, std::random_access_iterator3d_tag > |
| struct | Sobely |
| struct | __sobelz |
| struct | __sobelz< Real, std::random_access_iterator_tag > |
| struct | __sobelz< Real, std::random_access_iterator3d_tag > |
| struct | Sobelz |
| struct | __dv |
| struct | __dv< Real, std::random_access_iterator_tag > |
| struct | __dv< Real, std::random_access_iterator2d_tag > |
| struct | __dv< Real, std::random_access_iterator3d_tag > |
| struct | __dv< Real, std::random_access_iterator4d_tag > |
| dv first derivative in the direction of v. 4d extensions. | |
| struct | Dv |
| struct | __grad |
| struct | __grad< Real, std::random_access_iterator2d_tag > |
| struct | __grad< Real, std::random_access_iterator3d_tag > |
| struct | __grad< Real, std::random_access_iterator4d_tag > |
| gradient norm. 4d extensions. | |
| struct | Grad |
| struct | __dxx |
| struct | __dxx< Real, std::random_access_iterator_tag > |
| struct | __dxx< Real, std::random_access_iterator2d_tag > |
| struct | __dxx< Real, std::random_access_iterator3d_tag > |
| struct | __dxx< Real, std::random_access_iterator4d_tag > |
| dxx local derivatives. 4d extensions. | |
| struct | Dxx |
| struct | __dyy |
| struct | __dyy< Real, std::random_access_iterator_tag > |
| struct | __dyy< Real, std::random_access_iterator2d_tag > |
| struct | __dyy< Real, std::random_access_iterator3d_tag > |
| struct | __dyy< Real, std::random_access_iterator4d_tag > |
| dyy local derivatives. 4d extensions. | |
| struct | Dyy |
| struct | __dzz |
| struct | __dzz< Real, std::random_access_iterator_tag > |
| struct | __dzz< Real, std::random_access_iterator2d_tag > |
| struct | __dzz< Real, std::random_access_iterator3d_tag > |
| struct | __dzz< Real, std::random_access_iterator4d_tag > |
| dzz local derivatives. 4d extensions. | |
| struct | Dzz |
| struct | __dtt |
| dtt local derivatives. 4d extensions. | |
| struct | __dtt< Real, std::random_access_iterator_tag > |
| struct | __dtt< Real, std::random_access_iterator2d_tag > |
| struct | __dtt< Real, std::random_access_iterator3d_tag > |
| struct | __dtt< Real, std::random_access_iterator4d_tag > |
| struct | Dtt |
| struct | __dxy |
| struct | __dxy< Real, std::random_access_iterator_tag > |
| struct | __dxy< Real, std::random_access_iterator2d_tag > |
| struct | __dxy< Real, std::random_access_iterator3d_tag > |
| struct | Dxy |
| struct | __dxz |
| struct | __dxz< Real, std::random_access_iterator_tag > |
| struct | __dxz< Real, std::random_access_iterator3d_tag > |
| struct | Dxz |
| struct | __dyz |
| struct | __dyz< Real, std::random_access_iterator_tag > |
| struct | __dyz< Real, std::random_access_iterator3d_tag > |
| struct | Dyz |
| struct | __dxy_w |
| struct | __dxy_w< Real, std::random_access_iterator_tag > |
| struct | __dxy_w< Real, std::random_access_iterator2d_tag > |
| struct | __dxy_w< Real, std::random_access_iterator3d_tag > |
| struct | Dxy_W |
| struct | __div |
| struct | __div< Real, std::random_access_iterator_tag > |
| struct | __div< Real, std::random_access_iterator2d_tag > |
| struct | __div< Real, std::random_access_iterator3d_tag > |
| struct | __div< Real, std::random_access_iterator4d_tag > |
| divergence local derivatives. 4d extensions. | |
| struct | Div |
| struct | __lap |
| struct | __lap< Real, std::random_access_iterator_tag > |
| struct | __lap< Real, std::random_access_iterator2d_tag > |
| struct | __lap< Real, std::random_access_iterator3d_tag > |
| struct | __lap< Real, std::random_access_iterator4d_tag > |
| local laplacian. 4d extensions. | |
| struct | Lap |
| struct | __lap_8c |
| struct | __lap_8c< Real, std::random_access_iterator2d_tag > |
| struct | Lap8 |
| struct | LapLindeberg |
| struct | __iee_sapiro |
| struct | __iee_sapiro< Real, std::random_access_iterator2d_tag > |
| struct | __iee_sapiro< Real, std::random_access_iterator3d_tag > |
| struct | Iee_Sapiro |
| struct | __iee_lucido |
| struct | __iee_lucido< Real, std::random_access_iterator2d_tag > |
| struct | Iee_Lucido |
| struct | __iee_augereau |
| struct | __iee_augereau< Real, std::random_access_iterator2d_tag > |
| struct | Iee_Augereau |
| struct | __iee_alvarez |
| struct | __iee_alvarez< Real, std::random_access_iterator2d_tag > |
| struct | Iee_Alvarez |
| struct | __iee_alvarez2 |
| struct | __iee_alvarez2< Real, std::random_access_iterator2d_tag > |
| struct | Iee_Alvarez2 |
| struct | __iee_cohignac |
| struct | __iee_cohignac< Real, std::random_access_iterator2d_tag > |
| struct | Iee_Cohignac |
| struct | __inn_sapiro |
| struct | __inn_sapiro< Real, std::random_access_iterator2d_tag > |
| struct | __inn_sapiro< Real, std::random_access_iterator3d_tag > |
| struct | Inn_Sapiro |
| struct | __inn_lucido |
| struct | __inn_lucido< Real, std::random_access_iterator2d_tag > |
| struct | Inn_Lucido |
| struct | __inn_augereau |
| struct | __inn_augereau< Real, std::random_access_iterator2d_tag > |
| struct | Inn_Augereau |
| struct | __inn_alvarez |
| struct | __inn_alvarez< Real, std::random_access_iterator2d_tag > |
| struct | Inn_Alvarez |
| struct | __inn_alvarez2 |
| struct | __inn_alvarez2< Real, std::random_access_iterator2d_tag > |
| struct | Inn_Alvarez2 |
| struct | __inn_cohignac |
| struct | __inn_cohignac< Real, std::random_access_iterator2d_tag > |
| struct | Inn_Cohignac |
| struct | __dvv |
| struct | __dvv< Real, std::random_access_iterator_tag > |
| struct | __dvv< Real, std::random_access_iterator2d_tag > |
| struct | __dvv< Real, std::random_access_iterator3d_tag > |
| struct | Dvv |
| struct | __minmodx |
| struct | __minmodx< Real, std::random_access_iterator2d_tag > |
| struct | __minmodx< Real, std::random_access_iterator3d_tag > |
| struct | Minmodx |
| struct | __minmody |
| struct | __minmody< Real, std::random_access_iterator2d_tag > |
| struct | __minmody< Real, std::random_access_iterator3d_tag > |
| struct | Minmody |
| struct | __minmodz |
| struct | __minmodz< Real, std::random_access_iterator2d_tag > |
| struct | __minmodz< Real, std::random_access_iterator3d_tag > |
| struct | Minmodz |
| struct | __gradminus_OS |
| struct | __gradminus_OS< Real, std::random_access_iterator2d_tag > |
| struct | __gradminus_OS< Real, std::random_access_iterator3d_tag > |
| struct | Gradminus_OS |
| struct | __gradplus_OS |
| struct | __gradplus_OS< Real, std::random_access_iterator2d_tag > |
| struct | __gradplus_OS< Real, std::random_access_iterator3d_tag > |
| struct | Gradplus_OS |
| struct | __gradminus_BM |
| struct | __gradminus_BM< Real, std::random_access_iterator2d_tag > |
| struct | __gradminus_BM< Real, std::random_access_iterator3d_tag > |
| struct | Gradminus_BM |
| struct | __gradplus_BM |
| struct | __gradplus_BM< Real, std::random_access_iterator2d_tag > |
| struct | __gradplus_BM< Real, std::random_access_iterator3d_tag > |
| struct | Gradplus_BM |
| struct | __gradminus_minmod |
| struct | __gradminus_minmod< Real, std::random_access_iterator2d_tag > |
| struct | __gradminus_minmod< Real, std::random_access_iterator3d_tag > |
| struct | Gradminus_minmod |
| struct | Gradplus_minmod |
| struct | __min_curv |
| struct | __min_curv< Real, std::random_access_iterator_tag > |
| struct | __min_curv< Real, std::random_access_iterator2d_tag > |
| struct | Min_Curv |
| struct | __max_curv |
| struct | __max_curv< Real, std::random_access_iterator_tag > |
| struct | __max_curv< Real, std::random_access_iterator2d_tag > |
| struct | Max_Curv |
| struct | __mean_curv |
| struct | __mean_curv< Real, std::random_access_iterator_tag > |
| struct | __mean_curv< Real, std::random_access_iterator2d_tag > |
| struct | __mean_curv< Real, std::random_access_iterator3d_tag > |
| struct | Mean_Curv |
| struct | __total_curv |
| struct | __total_curv< Real, std::random_access_iterator_tag > |
| struct | __total_curv< Real, std::random_access_iterator2d_tag > |
| struct | __total_curv< Real, std::random_access_iterator3d_tag > |
| struct | Total_Curv |
| struct | __lambda1_curv |
| struct | __lambda1_curv< Real, std::random_access_iterator_tag > |
| struct | __lambda1_curv< Real, std::random_access_iterator2d_tag > |
| struct | Lambda1_Curv |
| struct | __lambda2_curv |
| struct | __lambda2_curv< Real, std::random_access_iterator_tag > |
| struct | __lambda2_curv< Real, std::random_access_iterator2d_tag > |
| struct | Lambda2_Curv |
| struct | __iso_curv |
| struct | __iso_curv< Real, std::random_access_iterator_tag > |
| struct | __iso_curv< Real, std::random_access_iterator2d_tag > |
| struct | Iso_Curv |
| struct | __courant_line_curv |
| struct | __courant_line_curv< Real, std::random_access_iterator_tag > |
| struct | __courant_line_curv< Real, std::random_access_iterator2d_tag > |
| struct | Courant_Line_Curv |
| struct | __delta_g_curv |
| struct | __delta_g_curv< Real, std::random_access_iterator_tag > |
| struct | __delta_g_curv< Real, std::random_access_iterator2d_tag > |
| struct | Delta_G_Curv |
| struct | range_fun_interab |
| Functor object uses to change the range of container according to an affine transformation. More... | |
| struct | range_fun_inter01 |
| Functor object uses to change the range of container into [0,1]. More... | |
| struct | range_fun_inter0255 |
| Functor object uses to change the range of container into [0,255]. More... | |
| struct | range_fun_inter0b |
| Functor object uses to change the range of container into [0,b]. More... | |
| struct | range_fun_normal |
| Functor object uses to change the range of container applying normal distribution. More... | |
| struct | range_fun_sigmoide |
| Functor object uses to change the range of container applying sigmoide distribution. More... | |
| struct | range_fun_sigmoideb |
| Functor object uses to change the range of container applying sigmoide distribution between [0,b]. More... | |
| struct | funLM_bp |
| Function to compute the backprojection of the 3d world point corresponding to the backprojection of an image point using the Levenberg-Marquadt algorithm. More... | |
| struct | funLM_DLT |
| Function to compute the camera model of distortion using the Levenberg-Marquadt algorithm. More... | |
| struct | LMDerivFunctor |
| generic derivative functor More... | |
| struct | saxpy |
Computes the saxpy ("scalar a x plus b") operation: ( 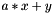 ) between two values. More... ) between two values. More... | |
| struct | z1conjz2 |
Computes the complex operation: ( 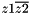 ) between two complex values z1 and z2. More... ) between two complex values z1 and z2. More... | |
| struct | conjz1z2 |
Computes the complex operation: ( 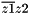 ) between two complex values z1 and z2. More... ) between two complex values z1 and z2. More... | |
| struct | __true_type |
| struct | __false_type |
| struct | __is_real |
| struct | __is_real< float > |
| struct | __is_real< double > |
| struct | __is_real< long double > |
| struct | __is_complex |
| struct | __is_complex< std::complex< float > > |
| struct | __is_complex< std::complex< double > > |
| struct | __is_complex< std::complex< long double > > |
| struct | lin_alg_traits |
| struct | lin_alg_traits< std::complex< _Tp > > |
| struct | un_real |
| Real functor. Return the real part of x. More... | |
| struct | un_imag |
| Imag functor. Return the imaginary part of x. More... | |
| struct | un_abs |
| Abs functor. Return the absolute value of x. More... | |
| struct | less_abs |
| Compare two element according to their absolute value. Return true if std::abs(__x) < std::abs( __y). More... | |
| struct | greater_abs |
| Compare two element according to their absolute value. Return true if std::abs(__x) > std::abs( __y). More... | |
| struct | mini |
| Computes the minimum value between two values. More... | |
| struct | maxi |
| Computes the maximum value between two values. More... | |
| struct | Sign |
| struct | complex_sign |
| struct | gt_it |
| struct | lt_it |
| struct | constants |
| A structure for numeric constants. More... | |
| struct | SafeN2C |
| struct | N2C |
| struct | SafePrev2C |
| struct | Prev2C |
| struct | SafeNext2C |
| struct | Next2C |
| struct | SafeN8C |
| struct | N8C |
| struct | SafePrev8C |
| struct | Prev8C |
| struct | SafeNext8C |
| struct | Next8C |
| struct | SafeN4C |
| struct | N4C |
| struct | SafeNext4C |
| struct | SafePrev4C |
| struct | Prev4C |
| struct | Next4C |
| struct | SafePseudoHexagonal |
| struct | PseudoHexagonal |
| struct | SafePrevPseudoHexagonal |
| struct | SafeNextPseudoHexagonal |
| struct | PrevPseudoHexagonal |
| struct | NextPseudoHexagonal |
| struct | SafeN6C |
| struct | N6C |
| struct | SafePrev6C |
| struct | Prev6C |
| struct | SafeNext6C |
| struct | Next6C |
| struct | SafeN26C |
| struct | N26C |
| struct | SafePrev26C |
| struct | Prev26C |
| struct | SafeNext26C |
| struct | Next26C |
| struct | SafeN18C |
| struct | N18C |
| struct | SafePrev18C |
| struct | Prev18C |
| struct | SafeNext18C |
| struct | Next18C |
| struct | SafeN4D8C |
| safe version of N4D8C neighborhood (only existing neighbors are returned) More... | |
| struct | N4D8C |
| N4D8C neighborhood. More... | |
| struct | SafePrev4D8C |
| safe version of previous N4D8C neighborhood (only previous and existing neighbors are returned) More... | |
| struct | Prev4D8C |
| previous N4D8C neighborhood (only previous neighbors are returned) More... | |
| struct | SafeNext4D8C |
| safe version of next N4D8C neighborhood (only next and existing neighbors are returned) More... | |
| struct | Next4D8C |
| next N4D8C neighborhood (only next neighbors are returned) More... | |
| struct | EvalBasis |
| struct | EvalPowerBasis |
| struct | EvalLegendreBasis |
| struct | EvalChebyshevBasis |
| struct | EvalPower2dBasis |
| struct | EvalPowerNdBasis |
| struct | Statistics |
| This is a structure to store descriptive statistics. More... | |
| struct | __cardinal |
| struct | __cardinal< Integer, std::random_access_iterator_tag > |
| struct | __cardinal< Integer, std::random_access_iterator2d_tag > |
| struct | __cardinal< Integer, std::random_access_iterator3d_tag > |
| struct | __median |
| struct | __median< std::random_access_iterator_tag > |
| class | GenericComparator |
| struct | binarize_fun |
| Functor object used to binarize a value. More... | |
| struct | threshold_fun |
| Functor object used to threshold a value. More... | |
| struct | db_threshold_fun |
| Functor object used to double-threshold a value. More... | |
| class | Array |
| This is a linear (one-dimensional) dynamic template container. This container statisfies the RandomAccessContainer concepts of the Standard Template Library (STL). More... | |
| class | stride_iterator |
| class | iterator2d_box |
| This is some iterator to iterate a 2d container into a slip::Box2d area defined by the indices of the 2d container. More... | |
| class | iterator2d_range |
| This is some iterator to iterate a 2d container into two Range defined by the indices and strides of the 2d container. More... | |
| class | const_iterator2d_box |
| This is some iterator to iterate a 2d container into a Box area defined by the indices of the 2d container. More... | |
| class | const_iterator2d_range |
| This is some iterator to iterate a 2d container into two Range defined by the indices and strides of the 2d container. More... | |
| class | DPoint2d |
| Difference of Point2D class, specialization of DPoint<CoordType,DIM> with DIM = 2. More... | |
| class | Point2d |
| This is a point2d class, a specialized version of Point<CoordType,DIM> with DIM = 2. More... | |
| class | Array2d |
| This is a two-dimensional dynamic and generic container. This container statisfies the BidirectionnalContainer concepts of the STL. It is also an 2d extension of the RandomAccessContainer concept. That is to say the bracket element access is replaced by the double bracket element access. More... | |
| class | Array3d |
| This is a three-dimensional dynamic and generic container. This container statisfies the BidirectionnalContainer concepts of the STL. It is also an 2d extension of the RandomAccessContainer concept. That is to say the bracket element access is replaced by the triple bracket element access. More... | |
| class | Array4d |
| This is a four-dimensional dynamic and generic container. This container statisfies the BidirectionnalContainer concepts of the STL. It is also an 4d extension of the RandomAccessContainer concept. That is to say the bracket element access is replaced by the quadruple bracket element access. More... | |
| struct | block |
| This is a linear (one-dimensional) static container. This container statisfies the RandomAccessContainer concepts of the Standard Template Library (STL). More... | |
| class | kstride_iterator |
| struct | block2d |
| This is a two-dimensional static and generic container. This container statisfies the BidirectionnalContainer concepts of the STL. It is also an 2d extension of the RandomAccessContainer concept. That is to say the bracket element access is replaced by the double bracket element access. More... | |
| class | block3d |
| This a three-dimensional static and generic container. This container statisfies the BidirectionnalContainer concepts of the STL. It is also an 3d extension of the RandomAccessContainer concept. That is to say the bracket element access is replaced by the triple bracket element access. More... | |
| class | block4d |
| This a four-dimensional static and generic container. This container statisfies the BidirectionnalContainer concepts of the STL. It is also an 4d extension of the RandomAccessContainer concept. That is to say the bracket element access is replaced by the quadruple bracket element access. More... | |
| class | Point |
| Define an abstract Point structure. More... | |
| class | DPoint |
| Define an abstract DPoint structure. More... | |
| class | Box |
| Define an abstract Box structure. More... | |
| class | Box1d |
| This is a Box1d class, a specialized version of slip::Box<CoordType,DIM> with DIM = 1. More... | |
| class | Box2d |
| This is a Box2d class, a specialized version of slip::Box<CoordType,DIM> with DIM = 2. More... | |
| class | Box3d |
| This is a Box3d class, a specialized version of slip::Box<CoordType,DIM> with DIM = 3. More... | |
| class | Box4d |
| This is a Box4d class, a specialized version of slip::Box<CoordType,DIM> with DIM = 4. More... | |
| class | CameraModel |
| Define an abstract CameraModel class. More... | |
| class | Color |
| This is a Color struct. More... | |
| class | ColorHyperVolume |
| This is a color hyper volume (4D) class. This container defines STL Bidirectionnal iterators begin and end. It defines also 4d extensions of the RandomAccess Iterators called first_front_upper_left and last_back_bottom_right(). As a consequence, the bracket element access is replaced by the triple bracket element access. It is a specialization of GenericMulitComponent4d using Color blocks. More... | |
| class | ColorImage |
| This is a color image class. This container statisfies the BidirectionnalContainer concepts of the STL. It is also an 2d extension of the RandomAccessContainer concept. That is to say the bracket element access is replaced by the double bracket element access. It is a specialization of GenericMulitComponent2d using Color blocks. Moreover it contains image read/write operations. These operations are done using the ImageMagick library. More... | |
| class | Colormap |
| Colormap container. This is a linear (one-dimensional) dynamic template container. This container statisfies the RandomAccessContainer concepts of the Standard Template Library (STL). More... | |
| class | ColorVolume |
| This is a color volume class. This container defines STL Bidirectionnal iterators begin and end. It defines also 3d extensions of the RandomAccess Iterators called front_upper_left and back_bottom_right(). As a consequence, the bracket element access is replaced by the triple bracket element access. It is a specialization of GenericMulitComponent3d using Color blocks. More... | |
| class | component_iterator2d_box |
| This is some iterator to iterate a 2d MultiComponentContainer into a Box area defined by the indices of the 2d container. More... | |
| class | const_component_iterator2d_box |
| This is some iterator to iterate a 2d MultiComponentContainer into a Box area defined by the indices of the 2d container. More... | |
| class | component_iterator2d_range |
| This is some iterator to iterate a 2d container into two Range defined by the indices and strides of the 2d container. More... | |
| class | const_component_iterator2d_range |
| This is some iterator to iterate a 2d container into two Range defined by the indices and strides of the 2d container. More... | |
| class | component_iterator3d_box |
| This is some iterator to iterate a 3d MultiComponentContainer into a Box area defined by the indices of the 3d container. More... | |
| class | const_component_iterator3d_box |
| This is some iterator to iterate a 3d MultiComponentContainer into a Box area defined by the indices of the 3d container. More... | |
| class | component_iterator3d_range |
| This is some iterator to iterate a 3d container into two Range defined by the indices and strides of the 3d container. More... | |
| class | const_component_iterator3d_range |
| This is some iterator to iterate a 3d container into two Range defined by the indices and strides of the 3d container. More... | |
| class | component_iterator4d_box |
| This is some iterator to iterate a 4d MultiComponentContainer into a Box area defined by the indices of the 4d container. More... | |
| class | const_component_iterator4d_box |
| This is some iterator to iterate a 4d MultiComponentContainer into a Box area defined by the indices of the 4d container. More... | |
| class | component_iterator4d_range |
| This is some iterator to iterate a 4d container into two Range defined by the indices and strides of the 4d container. More... | |
| class | const_component_iterator4d_range |
| This is some iterator to iterate a 4d container into two Range defined by the indices and strides of the 4d container. More... | |
| struct | __container_iterator_cast |
| struct | __container_iterator_cast< std::random_access_iterator_tag > |
| struct | __container_iterator_cast< std::random_access_iterator2d_tag > |
| struct | __container_iterator_cast< std::random_access_iterator3d_tag > |
| struct | __reverse_container_iterator_cast |
| struct | __reverse_container_iterator_cast< std::random_access_iterator_tag > |
| struct | __reverse_container_iterator_cast< std::random_access_iterator2d_tag > |
| struct | __reverse_container_iterator_cast< std::random_access_iterator3d_tag > |
| struct | __container_iterator_castR |
| struct | __container_iterator_castR< std::random_access_iterator_tag > |
| struct | __container_iterator_castR< std::random_access_iterator2d_tag > |
| struct | __container_iterator_castR< std::random_access_iterator3d_tag > |
| class | CUFTree |
| Define an union find tree. More... | |
| class | DenseVector2dField2d |
| This is a Dense Vector2d Field. This container statisfies the BidirectionnalContainer concepts of the STL. It is also an 2d extension of the RandomAccessContainer concept. That is to say the bracket element access is replaced by the double bracket element access. It is a specialization of GenericMultiComponent2d using Vector2d blocks. It implements arithmetic and mathematical operators and read/write methods (tecplot and gnuplot file format...). Contrary to slip::RegularVector2dField2d, this container is not associated with a grid. More... | |
| class | DenseVector3dField2d |
| This is a dense 2d Field containing Vector3d. This container statisfies the BidirectionnalContainer concepts of the STL. It is also an 2d extension of the RandomAccessContainer concept. That is to say the bracket element access is replaced by the double bracket element access. It is a specialization of GenericMultiComponent2d using Vector3d blocks. It implements arithmetic and mathematical operators and read/write methods (tecplot and gnuplot file format...). More... | |
| class | iterator3d_box |
| This is some iterator to iterate a 3d container into a Box area defined by the subscripts of the 3d container. More... | |
| class | iterator3d_range |
| This is some iterator to iterate a 3d container into two Range defined by the indices and strides of the 3d container. More... | |
| class | const_iterator3d_box |
| This is some iterator to iterate a 3d container into a Box area defined by the subscripts of the 3d container. More... | |
| class | const_iterator3d_range |
| This is some iterator to iterate a 3d container into two Range defined by the indices and strides of the 3d container. More... | |
| class | DPoint3d |
| Difference of Point3D class, specialization of DPoint<CoordType,DIM> with DIM = 3. More... | |
| class | Point3d |
| This is a point3d class, a specialized version of Point<CoordType,DIM> with DIM = 3. More... | |
| class | DenseVector3dField3d |
| This is a Dense Vector3d Field. This container statisfies the BidirectionnalContainer concepts of the STL. It is also an 3d extension of the RandomAccessContainer concept. That is to say the bracket element access is replaced by the triple bracket element access. It is a specialization of GenericMultiComponent3d using Vector3d blocks. It implements arithmetic and mathematical operators and read/write methods (tecplot and gnuplot file format...). Contrary to slip::RegularVector3dField3d, this container is not associated with a grid. More... | |
| struct | DistStruct |
| class | DistortionCamera |
| Define a DistortionCamera class. More... | |
| class | DPoint1d |
| Difference of Point1D class, specialization of DPoint<CoordType,DIM> with DIM = 1. More... | |
| class | DPoint4d |
| Difference of Point4D class, specialization of DPoint<CoordType,DIM> with DIM = 4. More... | |
| class | slip_exception |
| standard exception extension name have been changed to eliminate conflicts with QT More... | |
| class | GenericMultiComponent2d |
| This is a GenericMultiComponent2d class. This container statisfies the BidirectionnalContainer concepts of the STL. It is also an 2d extension of the RandomAccessContainer concept. That is to say the bracket element access is replaced by the double bracket element access. Data are stored using a Matrix of Block. It is essentially an internal class used to define slip::ColorImage, slip::MultispectralImage, slip::DenseVector2dField2d, slip::DenseVector3dField2d. But it can be used to define other 2d Multicomponent structures. More... | |
| class | Matrix |
| Numerical matrix class. This container statisfies the BidirectionnalContainer concepts of the STL. It is also an 2d extension of the RandomAccessContainer concept. That is to say the bracket element access is replaced by the double bracket element access. It extends the interface of Array2d adding arithmetical: +=, -=, *=, /=,+,-,/,*... and mathematical operators: min, max, abs, sqrt, cos, acos, sin, asin, tan, atan, exp, log, cosh, sinh, tanh, log10, sum, apply... More... | |
| class | GenericMultiComponent3d |
| This is a GenericMultiComponent3d class. This container statisfies the BidirectionnalContainer concepts of the STL. It is also an 3d extension of the RandomAccessContainer concept. That is to say the bracket element access is replaced by the triple bracket element access. Data are stored using a Matrix3d of Block. It is essentially an internal class used to define slip::DenseVector3dField3d. But it can be used to define other 3d Multicomponent structures. More... | |
| class | Matrix3d |
| Numerical matrix3d class. This container statisfies the RandomAccessContainer concepts of the STL except the simple bracket which is replaced by a double bracket. It extends the interface of Array3d adding arithmetical: +=, -=, *=, /=,+,-,/,*... and mathematical operators : min, max, abs, sqrt, cos, acos, sin, asin, tan, atan, exp, log, cosh, sinh, tanh, log10, sum, apply... More... | |
| struct | L2_dist< typename Block::value_type, slip::GenericMultiComponent3d< Block > > |
| class | Point4d |
| This is a point4d class, a specialized version of Point<CoordType,DIM> with DIM = 4. More... | |
| class | GenericMultiComponent4d |
| This is a GenericMultiComponent4d class. This container statisfies the BidirectionnalContainer concepts of the STL. It is also an 4d extension of the RandomAccessContainer concept. That is to say the bracket element access is replaced by the triple bracket element access. Data are stored using a Matrix4d of Block. This class can be used to define 4d Multicomponent structures. More... | |
| class | Matrix4d |
| Numerical matrix4d class. This container statisfies the RandomAccessContainer concepts of the STL except the simple bracket which is replaced by a double bracket. It extends the interface of Array4d adding arithmetical: +=, -=, *=, /=,+,-,/,*... and mathematical operators : min, max, abs, sqrt, cos, acos, sin, asin, tan, atan, exp, log, cosh, sinh, tanh, log10, sum, apply... More... | |
| class | Range |
| This is a Range class. More... | |
| class | GrayscaleImage |
| This is a grayscaleimage class. This is a two-dimensional dynamic and generic container. This container statisfies the BidirectionnalContainer concepts of the STL. It is also an 2d extension of the RandomAccessContainer concept. That is to say the bracket element access is replaced by the double bracket element access. Data are stored using a Matrix class. It extends the interface of Matrix adding image read/write operations. These operations are done using the ImageMagick library. More... | |
| class | HyperVolume |
| Numerical container class This is a four-dimensional dynamic and generic container. This container satisfies the BidirectionnalContainer concepts of the STL. It is also an 4d extension of the RandomAccessContainer concept. That is to say the bracket element access is replaced by the triple bracket element access. Data are stored using a Matrix4d class. It extends the interface of Matrix4d adding image read/write operations. These operations are done using the ImageMagick library. More... | |
| class | iterator3d_plane |
| This is some iterator to iterate a 3d container into a plane area defined by the subscripts of the 3d container. More... | |
| class | const_iterator3d_plane |
| This is some iterator to iterate a 3d container into a plane area defined by the subscripts of the 3d container. More... | |
| class | iterator4d_box |
| This is some iterator to iterate a 4d container into a Box area defined by the subscripts of the 4d container. More... | |
| class | const_iterator4d_box |
| This is some iterator to iterate a 4d container into a Box area defined by the subscripts of the 4d container. More... | |
| class | iterator4d_range |
| This is some iterator to iterate a 4d container into two Range defined by the indices and strides of the 4d container. More... | |
| class | const_iterator4d_range |
| Some const iterator to iterate a 4d container into two Range defined by the indices and strides of the 4d container. More... | |
| struct | kvector |
| This is a linear (one-dimensional) static vector. This container statisfies the RandomAccessContainer concepts of the Standard Template Library (STL). It extends the interface of Array adding arithmetical: +=, -=, *=, /=, +,-,/,*... and mathematical operators : min, max, abs, sqrt, cos, acos, sin, asin, tan, atan, exp, log, cosh, sinh, tanh, log10, sum, apply, Euclidean norm, L1 norm, L2 norm... More... | |
| class | MultispectralImage |
| This is a Multi Spectral Image container. This container statisfies the BidirectionnalContainer concepts of the STL. It is also an 2d extension of the RandomAccessContainer concept. That is to say the bracket element access is replaced by the double bracket element access. It is a specialization of slip::GenericMulitComponent2d using blocks. More... | |
| struct | Monomial |
| Numerical Monomial structure. More... | |
| class | MultivariatePolynomial |
| Numerical MultivariatePolynomial class. More... | |
| class | PinholeCamera |
| Define a PinholeCamera class. More... | |
| class | PinholeDLTCamera |
| Define a PinholeDLTCamera class. More... | |
| class | PinholeFaugerasCamera |
| Define a PinholeFaugerasCamera class. More... | |
| class | Point1d |
| This is a point1d class, a specialized version of Point<CoordType,DIM> with DIM = 1. More... | |
| class | Polynomial |
Numerical Polynomial class. This container statisfies the RandomAccessContainer concepts of the STL The coefficients of the polynomial 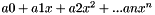 are ordered as follows : (a0,a1,...,an) More... are ordered as follows : (a0,a1,...,an) More... | |
| struct | __container_size |
| struct | __container_size< Container, std::random_access_iterator_tag > |
| struct | __container_size< Container, std::random_access_iterator2d_tag > |
| struct | __container_size< Container, std::random_access_iterator3d_tag > |
| struct | ContainerSize |
| struct | __container_resolution |
| struct | __container_resolution< Container, std::random_access_iterator_tag > |
| struct | __container_resolution< Container, std::random_access_iterator2d_tag > |
| struct | __container_resolution< Container, std::random_access_iterator3d_tag > |
| struct | ContainerResolution |
| struct | __container_allocator |
| struct | __container_allocator< Container, std::random_access_iterator_tag > |
| struct | __container_allocator< Container, std::random_access_iterator2d_tag > |
| struct | __container_allocator< Container, std::random_access_iterator3d_tag > |
| struct | ContainerAllocator |
| struct | __pyramid_allocator |
| struct | __pyramid_allocator< Container, std::random_access_iterator_tag > |
| struct | __pyramid_allocator< Container, std::random_access_iterator2d_tag > |
| struct | __pyramid_allocator< Container, std::random_access_iterator3d_tag > |
| struct | Pyramid_Allocator |
| struct | __pyramid_copy |
| struct | __pyramid_copy< Container, std::random_access_iterator_tag > |
| struct | __pyramid_copy< Container, std::random_access_iterator2d_tag > |
| struct | __pyramid_copy< Container, std::random_access_iterator3d_tag > |
| struct | Pyramid_Copy |
| class | Pyramid |
| This is container to handle a pyramid of containers. More... | |
| class | RegularVector2dField2d |
| This is a 2d Field containing slip::Vector2d associated with a regular grid. This container statisfies the BidirectionnalContainer concepts of the STL. It is also an 2d extension of the RandomAccessContainer concept. That is to say the bracket element access is replaced by the double bracket element access. It is a specialization of GenericMultiComponent2d using Vector2d blocks. It implements arithmetic and mathematical operators (divergence, vorticity, derivative...) and read/write methods (tecplot and gnuplot file format). The points of the Vector field grid are assumed to be spaced by two regular steps. The inital point (closest point from the physical axis origin) of the grid is also stored within the data structure. More... | |
| class | RegularVector3dField3d |
| This is a Regular Vector3d Field. This container statisfies the BidirectionnalContainer concepts of the STL. It is also an 3d extension of the RandomAccessContainer concept. That is to say the bracket element access is replaced by the triple bracket element access. It is a specialization of GenericMultiComponent3d using slip::Vector3d blocks. It implements arithmetic and mathematical operators (divergence, vorticity, derivative...) and read/write methods (tecplot file format). The points of the Vector field grid are assumed to be spaced by two regular steps. The inital point (closest point from the physical axis origin) of the grid is also stored within the data structure. More... | |
| class | Signal |
| Numerical Signal class. This container statisfies the RandomAccessContainer concepts of the Standard Template Library (STL). Data are stored using a Vector class. It extends the interface of Vector adding signal read/write operations. More... | |
| class | SoloffCamera |
| Define a SoloffCamera class. More... | |
| class | Vector |
| Numerical Vector class. This container statisfies the RandomAccessContainer concepts of the Standard Template Library (STL). It extends the interface of Array adding arithmetical: +=, -=, *=, /=,+,-,/,*... and mathematical operators : min, max, abs, sqrt, cos, acos, sin, asin, tan, atan, exp, log, cosh, sinh, tanh, log10, sum, apply... More... | |
| class | Vector2d |
| This is a Vector2d struct. It is a specialization of kvector. It implements some peculiar 2d operations. More... | |
| struct | AE_rad |
| Computes the angular error usually used in optical flow estimation evaluations:
where : More... | |
| struct | AE_deg |
| Computes the angular error usually used in optical flow estimation evaluations:
where: More... | |
| class | Vector3d |
| This is a Vector3d struct. It is a specialization of kvector. It implements some specific 3d operations. More... | |
| class | Vector4d |
| This is a Vector4d struct. It is a specialization of kvector. It implements some specific 4d operations. More... | |
| class | Volume |
| Numerical volume class This is a two-dimensional dynamic and generic container. This container statisfies the BidirectionnalContainer concepts of the STL. It is also an 3d extension of the RandomAccessContainer concept. That is to say the bracket element access is replaced by the triple bracket element access. Data are stored using a Matrix3d class. It extends the interface of Matrix3d adding image read/write operations. These operations are done using the ImageMagick library. More... | |
| class | AvReader |
| AvReader, inherited from ContainerReader, is a reader for videos. More... | |
| class | AvWriter |
| AvWriter is a video writer. More... | |
| class | ContainerReader |
| ContainerReader is the base class of the readers classes. All readers are working the same way: More... | |
| class | ContainerWriter |
| ContainerWriter is the base class of the writer classes. All the writers are working the same way: More... | |
| class | FITSReader |
| FITSReader, inherited from ContainerReader, is a reader of fits files (only Single Image FITS file as the reader read only the PHDU) More... | |
| class | FITSWriter |
| FITSWriter is a fits writer. More... | |
| class | JpegReader |
| JpegReader, inherited from ContainerReader, is a reader for jpeg images. More... | |
| class | JpegWriter |
| JpegWriter is the jpeg image writer. More... | |
| class | NetCDFReader |
| NetCDFReader, inherited from ContainerReader, is a reader of netcdf files. More... | |
| class | NetCDFWriter |
| NetCDFWriter is a net. More... | |
| class | PngReader |
| PngReader, inherited from ContainerReader, is a reader for png images. More... | |
| struct | png_static_cast_func |
| class | PngWriter |
| PngWriter is the png image writer. More... | |
| class | WavReader |
| WavReader, inherited from ContainerReader, is a reader for wav audio files. More... | |
| class | WavWriter |
| WavWriter is the wave array writer. More... | |
Typedefs | |
| typedef slip::Array< double > | Array_d |
| double alias More... | |
| typedef slip::Array< float > | Array_f |
| float alias More... | |
| typedef slip::Array< long > | Array_l |
| long alias More... | |
| typedef slip::Array< unsigned long > | Array_ul |
| unsigned long alias More... | |
| typedef slip::Array< short > | Array_s |
| short alias More... | |
| typedef slip::Array< unsigned short > | Array_us |
| unsigned long alias More... | |
| typedef slip::Array< int > | Array_i |
| int alias More... | |
| typedef slip::Array< unsigned int > | Array_ui |
| unsigned int alias More... | |
| typedef slip::Array< char > | Array_c |
| char alias More... | |
| typedef slip::Array< unsigned char > | Array_uc |
| unsigned char alias More... | |
| typedef slip::Array2d< double > | Array2d_d |
| double alias More... | |
| typedef slip::Array2d< float > | Array2d_f |
| float alias More... | |
| typedef slip::Array2d< long > | Array2d_l |
| long alias More... | |
| typedef slip::Array2d < unsigned long > | Array2d_ul |
| unsigned long alias More... | |
| typedef slip::Array2d< short > | Array2d_s |
| short alias More... | |
| typedef slip::Array2d < unsigned short > | Array2d_us |
| unsigned long alias More... | |
| typedef slip::Array2d< int > | Array2d_i |
| int alias More... | |
| typedef slip::Array2d < unsigned int > | Array2d_ui |
| unsigned int alias More... | |
| typedef slip::Array2d< char > | Array2d_c |
| char alias More... | |
| typedef slip::Array2d < unsigned char > | Array2d_uc |
| unsigned char alias More... | |
| typedef slip::Array3d< double > | Array3d_d |
| double alias More... | |
| typedef slip::Array3d< float > | Array3d_f |
| float alias More... | |
| typedef slip::Array3d< long > | Array3d_l |
| long alias More... | |
| typedef slip::Array3d < unsigned long > | Array3d_ul |
| unsigned long alias More... | |
| typedef slip::Array3d< short > | Array3d_s |
| short alias More... | |
| typedef slip::Array3d < unsigned short > | Array3d_us |
| unsigned long alias More... | |
| typedef slip::Array3d< int > | Array3d_i |
| int alias More... | |
| typedef slip::Array3d < unsigned int > | Array3d_ui |
| unsigned int alias More... | |
| typedef slip::Array3d< char > | Array3d_c |
| char alias More... | |
| typedef slip::Array3d < unsigned char > | Array3d_uc |
| unsigned char alias More... | |
| typedef slip::Array4d< double > | Array4d_d |
| double alias More... | |
| typedef slip::Array4d< float > | Array4d_f |
| float alias More... | |
| typedef slip::Array4d< long > | Array4d_l |
| long alias More... | |
| typedef slip::Array4d < unsigned long > | Array4d_ul |
| unsigned long alias More... | |
| typedef slip::Array4d< short > | Array4d_s |
| short alias More... | |
| typedef slip::Array4d < unsigned short > | Array4d_us |
| unsigned long alias More... | |
| typedef slip::Array4d< int > | Array4d_i |
| int alias More... | |
| typedef slip::Array4d < unsigned int > | Array4d_ui |
| unsigned int alias More... | |
| typedef slip::Array4d< char > | Array4d_c |
| char alias More... | |
| typedef slip::Array4d < unsigned char > | Array4d_uc |
| unsigned char alias More... | |
| typedef slip::Color< double > | Color_d |
| double alias More... | |
| typedef slip::Color< float > | Color_f |
| float alias More... | |
| typedef slip::Color< long > | Color_l |
| long alias More... | |
| typedef slip::Color< unsigned long > | Color_ul |
| unsigned long alias More... | |
| typedef slip::Color< short > | Color_s |
| short alias More... | |
| typedef slip::Color< unsigned short > | Color_us |
| unsigned long alias More... | |
| typedef slip::Color< int > | Color_i |
| int alias More... | |
| typedef slip::Color< unsigned int > | Color_ui |
| unsigned int alias More... | |
| typedef slip::Color< char > | Color_c |
| char alias More... | |
| typedef slip::Color< unsigned char > | Color_uc |
| unsigned char alias More... | |
| typedef slip::ColorHyperVolume < double > | ColorHyperVolume_d |
| double alias More... | |
| typedef slip::ColorHyperVolume < float > | ColorHyperVolume_f |
| float alias More... | |
| typedef slip::ColorHyperVolume < long > | ColorHyperVolume_l |
| long alias More... | |
| typedef slip::ColorHyperVolume < unsigned long > | ColorHyperVolume_ul |
| unsigned long alias More... | |
| typedef slip::ColorHyperVolume < short > | ColorHyperVolume_s |
| short alias More... | |
| typedef slip::ColorHyperVolume < unsigned short > | ColorHyperVolume_us |
| unsigned long alias More... | |
| typedef slip::ColorHyperVolume < int > | ColorHyperVolume_i |
| int alias More... | |
| typedef slip::ColorHyperVolume < unsigned int > | ColorHyperVolume_ui |
| unsigned int alias More... | |
| typedef slip::ColorHyperVolume < char > | ColorHyperVolume_c |
| char alias More... | |
| typedef slip::ColorHyperVolume < unsigned char > | ColorHyperVolume_uc |
| unsigned char alias More... | |
| typedef slip::ColorImage< double > | ColorImage_d |
| double alias More... | |
| typedef slip::ColorImage< float > | ColorImage_f |
| float alias More... | |
| typedef slip::ColorImage< long > | ColorImage_l |
| long alias More... | |
| typedef slip::ColorImage < unsigned long > | ColorImage_ul |
| unsigned long alias More... | |
| typedef slip::ColorImage< short > | ColorImage_s |
| short alias More... | |
| typedef slip::ColorImage < unsigned short > | ColorImage_us |
| unsigned long alias More... | |
| typedef slip::ColorImage< int > | ColorImage_i |
| int alias More... | |
| typedef slip::ColorImage < unsigned int > | ColorImage_ui |
| unsigned int alias More... | |
| typedef slip::ColorImage< char > | ColorImage_c |
| char alias More... | |
| typedef slip::ColorImage < unsigned char > | ColorImage_uc |
| unsigned char alias More... | |
| typedef slip::Colormap< double > | Colormap_d |
| double alias More... | |
| typedef slip::Colormap< float > | Colormap_f |
| float alias More... | |
| typedef slip::Colormap< long > | Colormap_l |
| long alias More... | |
| typedef slip::Colormap < unsigned long > | Colormap_ul |
| unsigned long alias More... | |
| typedef slip::Colormap< short > | Colormap_s |
| short alias More... | |
| typedef slip::Colormap < unsigned short > | Colormap_us |
| unsigned long alias More... | |
| typedef slip::Colormap< int > | Colormap_i |
| int alias More... | |
| typedef slip::Colormap < unsigned int > | Colormap_ui |
| unsigned int alias More... | |
| typedef slip::Colormap< char > | Colormap_c |
| char alias More... | |
| typedef slip::Colormap < unsigned char > | Colormap_uc |
| unsigned char alias More... | |
| typedef slip::ColorVolume< double > | ColorVolume_d |
| double alias More... | |
| typedef slip::ColorVolume< float > | ColorVolume_f |
| float alias More... | |
| typedef slip::ColorVolume< long > | ColorVolume_l |
| long alias More... | |
| typedef slip::ColorVolume < unsigned long > | ColorVolume_ul |
| unsigned long alias More... | |
| typedef slip::ColorVolume< short > | ColorVolume_s |
| short alias More... | |
| typedef slip::ColorVolume < unsigned short > | ColorVolume_us |
| unsigned long alias More... | |
| typedef slip::ColorVolume< int > | ColorVolume_i |
| int alias More... | |
| typedef slip::ColorVolume < unsigned int > | ColorVolume_ui |
| unsigned int alias More... | |
| typedef slip::ColorVolume< char > | ColorVolume_c |
| char alias More... | |
| typedef slip::ColorVolume < unsigned char > | ColorVolume_uc |
| unsigned char alias More... | |
| typedef slip::DenseVector2dField2d < double > | DenseVector2dField2d_d |
| double alias More... | |
| typedef slip::DenseVector2dField2d < float > | DenseVector2dField2d_f |
| float alias More... | |
| typedef slip::DenseVector2dField2d < long > | DenseVector2dField2d_l |
| long alias More... | |
| typedef slip::DenseVector2dField2d < unsigned long > | DenseVector2dField2d_ul |
| unsigned long alias More... | |
| typedef slip::DenseVector2dField2d < short > | DenseVector2dField2d_s |
| short alias More... | |
| typedef slip::DenseVector2dField2d < unsigned short > | DenseVector2dField2d_us |
| unsigned long alias More... | |
| typedef slip::DenseVector2dField2d < int > | DenseVector2dField2d_i |
| int alias More... | |
| typedef slip::DenseVector2dField2d < unsigned int > | DenseVector2dField2d_ui |
| unsigned int alias More... | |
| typedef slip::DenseVector2dField2d < char > | DenseVector2dField2d_c |
| char alias More... | |
| typedef slip::DenseVector2dField2d < unsigned char > | DenseVector2dField2d_uc |
| unsigned char alias More... | |
| typedef slip::DenseVector3dField2d < double > | DenseVector3dField2d_d |
| double alias More... | |
| typedef slip::DenseVector3dField2d < float > | DenseVector3dField2d_f |
| float alias More... | |
| typedef slip::DenseVector3dField2d < long > | DenseVector3dField2d_l |
| long alias More... | |
| typedef slip::DenseVector3dField2d < unsigned long > | DenseVector3dField2d_ul |
| unsigned long alias More... | |
| typedef slip::DenseVector3dField2d < short > | DenseVector3dField2d_s |
| short alias More... | |
| typedef slip::DenseVector3dField2d < unsigned short > | DenseVector3dField2d_us |
| unsigned long alias More... | |
| typedef slip::DenseVector3dField2d < int > | DenseVector3dField2d_i |
| int alias More... | |
| typedef slip::DenseVector3dField2d < unsigned int > | DenseVector3dField2d_ui |
| unsigned int alias More... | |
| typedef slip::DenseVector3dField2d < char > | DenseVector3dField2d_c |
| char alias More... | |
| typedef slip::DenseVector3dField2d < unsigned char > | DenseVector3dField2d_uc |
| unsigned char alias More... | |
| typedef slip::DenseVector3dField3d < double > | DenseVector3dField3d_d |
| double alias More... | |
| typedef slip::DenseVector3dField3d < float > | DenseVector3dField3d_f |
| float alias More... | |
| typedef slip::DenseVector3dField3d < long > | DenseVector3dField3d_l |
| long alias More... | |
| typedef slip::DenseVector3dField3d < unsigned long > | DenseVector3dField3d_ul |
| unsigned long alias More... | |
| typedef slip::DenseVector3dField3d < short > | DenseVector3dField3d_s |
| short alias More... | |
| typedef slip::DenseVector3dField3d < unsigned short > | DenseVector3dField3d_us |
| unsigned long alias More... | |
| typedef slip::DenseVector3dField3d < int > | DenseVector3dField3d_i |
| int alias More... | |
| typedef slip::DenseVector3dField3d < unsigned int > | DenseVector3dField3d_ui |
| unsigned int alias More... | |
| typedef slip::DenseVector3dField3d < char > | DenseVector3dField3d_c |
| char alias More... | |
| typedef slip::DenseVector3dField3d < unsigned char > | DenseVector3dField3d_uc |
| unsigned char alias More... | |
| typedef slip::GrayscaleImage < double > | GrayscaleImage_d |
| double alias More... | |
| typedef slip::GrayscaleImage < float > | GrayscaleImage_f |
| float alias More... | |
| typedef slip::GrayscaleImage < long > | GrayscaleImage_l |
| long alias More... | |
| typedef slip::GrayscaleImage < unsigned long > | GrayscaleImage_ul |
| unsigned long alias More... | |
| typedef slip::GrayscaleImage < short > | GrayscaleImage_s |
| short alias More... | |
| typedef slip::GrayscaleImage < unsigned short > | GrayscaleImage_us |
| unsigned long alias More... | |
| typedef slip::GrayscaleImage< int > | GrayscaleImage_i |
| int alias More... | |
| typedef slip::GrayscaleImage < unsigned int > | GrayscaleImage_ui |
| unsigned int alias More... | |
| typedef slip::GrayscaleImage < char > | GrayscaleImage_c |
| char alias More... | |
| typedef slip::GrayscaleImage < unsigned char > | GrayscaleImage_uc |
| unsigned char alias More... | |
| typedef slip::HyperVolume< double > | HyperVolume_d |
| double alias More... | |
| typedef slip::HyperVolume< float > | HyperVolume_f |
| float alias More... | |
| typedef slip::HyperVolume< long > | HyperVolume_l |
| long alias More... | |
| typedef slip::HyperVolume < unsigned long > | HyperVolume_ul |
| unsigned long alias More... | |
| typedef slip::HyperVolume< short > | HyperVolume_s |
| short alias More... | |
| typedef slip::HyperVolume < unsigned short > | HyperVolume_us |
| unsigned long alias More... | |
| typedef slip::HyperVolume< int > | HyperVolume_i |
| int alias More... | |
| typedef slip::HyperVolume < unsigned int > | HyperVolume_ui |
| unsigned int alias More... | |
| typedef slip::HyperVolume< char > | HyperVolume_c |
| char alias More... | |
| typedef slip::HyperVolume < unsigned char > | HyperVolume_uc |
| unsigned char alias More... | |
| typedef slip::Matrix< double > | Matrix_d |
| double alias More... | |
| typedef slip::Matrix< float > | Matrix_f |
| float alias More... | |
| typedef slip::Matrix< long > | Matrix_l |
| long alias More... | |
| typedef slip::Matrix< unsigned long > | Matrix_ul |
| unsigned long alias More... | |
| typedef slip::Matrix< short > | Matrix_s |
| short alias More... | |
| typedef slip::Matrix< unsigned short > | Matrix_us |
| unsigned long alias More... | |
| typedef slip::Matrix< int > | Matrix_i |
| int alias More... | |
| typedef slip::Matrix< unsigned int > | Matrix_ui |
| unsigned int alias More... | |
| typedef slip::Matrix< char > | Matrix_c |
| char alias More... | |
| typedef slip::Matrix< unsigned char > | Matrix_uc |
| unsigned char alias More... | |
| typedef slip::Matrix3d< double > | Matrix3d_d |
| double alias More... | |
| typedef slip::Matrix3d< float > | Matrix3d_f |
| float alias More... | |
| typedef slip::Matrix3d< long > | Matrix3d_l |
| long alias More... | |
| typedef slip::Matrix3d < unsigned long > | Matrix3d_ul |
| unsigned long alias More... | |
| typedef slip::Matrix3d< short > | Matrix3d_s |
| short alias More... | |
| typedef slip::Matrix3d < unsigned short > | Matrix3d_us |
| unsigned long alias More... | |
| typedef slip::Matrix3d< int > | Matrix3d_i |
| int alias More... | |
| typedef slip::Matrix3d < unsigned int > | Matrix3d_ui |
| unsigned int alias More... | |
| typedef slip::Matrix3d< char > | Matrix3d_c |
| char alias More... | |
| typedef slip::Matrix3d < unsigned char > | Matrix3d_uc |
| unsigned char alias More... | |
| typedef slip::Matrix4d< double > | Matrix4d_d |
| double alias More... | |
| typedef slip::Matrix4d< float > | Matrix4d_f |
| float alias More... | |
| typedef slip::Matrix4d< long > | Matrix4d_l |
| long alias More... | |
| typedef slip::Matrix4d < unsigned long > | Matrix4d_ul |
| unsigned long alias More... | |
| typedef slip::Matrix4d< short > | Matrix4d_s |
| short alias More... | |
| typedef slip::Matrix4d < unsigned short > | Matrix4d_us |
| unsigned long alias More... | |
| typedef slip::Matrix4d< int > | Matrix4d_i |
| int alias More... | |
| typedef slip::Matrix4d < unsigned int > | Matrix4d_ui |
| unsigned int alias More... | |
| typedef slip::Matrix4d< char > | Matrix4d_c |
| char alias More... | |
| typedef slip::Matrix4d < unsigned char > | Matrix4d_uc |
| unsigned char alias More... | |
| typedef slip::Point1d< double > | Point1d_d |
| double alias More... | |
| typedef slip::Point1d< float > | Point1d_f |
| float alias More... | |
| typedef slip::Point1d< long > | Point1d_l |
| long alias More... | |
| typedef slip::Point1d < unsigned long > | Point1d_ul |
| unsigned long alias More... | |
| typedef slip::Point1d< short > | Point1d_s |
| short alias More... | |
| typedef slip::Point1d < unsigned short > | Point1d_us |
| unsigned long alias More... | |
| typedef slip::Point1d< int > | Point1d_i |
| int alias More... | |
| typedef slip::Point1d < unsigned int > | Point1d_ui |
| unsigned int alias More... | |
| typedef slip::Point1d< char > | Point1d_c |
| char alias More... | |
| typedef slip::Point1d < unsigned char > | Point1d_uc |
| unsigned char alias More... | |
| typedef slip::Point2d< double > | Point2d_d |
| double alias More... | |
| typedef slip::Point2d< float > | Point2d_f |
| float alias More... | |
| typedef slip::Point2d< long > | Point2d_l |
| long alias More... | |
| typedef slip::Point2d < unsigned long > | Point2d_ul |
| unsigned long alias More... | |
| typedef slip::Point2d< short > | Point2d_s |
| short alias More... | |
| typedef slip::Point2d < unsigned short > | Point2d_us |
| unsigned long alias More... | |
| typedef slip::Point2d< int > | Point2d_i |
| int alias More... | |
| typedef slip::Point2d < unsigned int > | Point2d_ui |
| unsigned int alias More... | |
| typedef slip::Point2d< char > | Point2d_c |
| char alias More... | |
| typedef slip::Point2d < unsigned char > | Point2d_uc |
| unsigned char alias More... | |
| typedef slip::Point3d< double > | Point3d_d |
| double alias More... | |
| typedef slip::Point3d< float > | Point3d_f |
| float alias More... | |
| typedef slip::Point3d< long > | Point3d_l |
| long alias More... | |
| typedef slip::Point3d < unsigned long > | Point3d_ul |
| unsigned long alias More... | |
| typedef slip::Point3d< short > | Point3d_s |
| short alias More... | |
| typedef slip::Point3d < unsigned short > | Point3d_us |
| unsigned long alias More... | |
| typedef slip::Point3d< int > | Point3d_i |
| int alias More... | |
| typedef slip::Point3d < unsigned int > | Point3d_ui |
| unsigned int alias More... | |
| typedef slip::Point3d< char > | Point3d_c |
| char alias More... | |
| typedef slip::Point3d < unsigned char > | Point3d_uc |
| unsigned char alias More... | |
| typedef slip::Point4d< double > | Point4d_d |
| double alias More... | |
| typedef slip::Point4d< float > | Point4d_f |
| float alias More... | |
| typedef slip::Point4d< long > | Point4d_l |
| long alias More... | |
| typedef slip::Point4d < unsigned long > | Point4d_ul |
| unsigned long alias More... | |
| typedef slip::Point4d< short > | Point4d_s |
| short alias More... | |
| typedef slip::Point4d < unsigned short > | Point4d_us |
| unsigned long alias More... | |
| typedef slip::Point4d< int > | Point4d_i |
| int alias More... | |
| typedef slip::Point4d < unsigned int > | Point4d_ui |
| unsigned int alias More... | |
| typedef slip::Point4d< char > | Point4d_c |
| char alias More... | |
| typedef slip::Point4d < unsigned char > | Point4d_uc |
| unsigned char alias More... | |
| typedef RegularVector2dField2d < double, double > | Regular2D3Cd |
| double alias More... | |
| typedef RegularVector2dField2d < float, double > | Regular2D3Cf |
| float alias More... | |
| typedef RegularVector2dField2d < double, double > | Regular2D3C_d |
| double alias More... | |
| typedef RegularVector2dField2d < float, double > | Regular2D3C_f |
| float alias More... | |
| typedef slip::RegularVector2dField2d < double, double > | RegularVector2dField2d_d |
| double alias More... | |
| typedef slip::RegularVector2dField2d < float, double > | RegularVector2dField2d_f |
| float alias More... | |
| typedef slip::RegularVector2dField2d < long, double > | RegularVector2dField2d_l |
| long alias More... | |
| typedef slip::RegularVector2dField2d < unsigned long, double > | RegularVector2dField2d_ul |
| unsigned long alias More... | |
| typedef slip::RegularVector2dField2d < short, double > | RegularVector2dField2d_s |
| short alias More... | |
| typedef slip::RegularVector2dField2d < unsigned short, double > | RegularVector2dField2d_us |
| unsigned long alias More... | |
| typedef slip::RegularVector2dField2d < int, double > | RegularVector2dField2d_i |
| int alias More... | |
| typedef slip::RegularVector2dField2d < unsigned int, double > | RegularVector2dField2d_ui |
| unsigned int alias More... | |
| typedef slip::RegularVector2dField2d < char, double > | RegularVector2dField2d_c |
| char alias More... | |
| typedef slip::RegularVector2dField2d < unsigned char, double > | RegularVector2dField2d_uc |
| unsigned char alias More... | |
| typedef RegularVector3dField3d < double, double > | Regular3D3Cd |
| double alias More... | |
| typedef RegularVector3dField3d < float, double > | Regular3D3Cf |
| float alias More... | |
| typedef RegularVector3dField3d < double, double > | Regular3D3C_d |
| double alias More... | |
| typedef RegularVector3dField3d < float, double > | Regular3D3C_f |
| float alias More... | |
| typedef slip::RegularVector3dField3d < double, double > | RegularVector3dField3d_d |
| double alias More... | |
| typedef slip::RegularVector3dField3d < float, float > | RegularVector3dField3d_f |
| float alias More... | |
| typedef slip::RegularVector3dField3d < long, double > | RegularVector3dField3d_l |
| long alias More... | |
| typedef slip::RegularVector3dField3d < unsigned long, double > | RegularVector3dField3d_ul |
| unsigned long alias More... | |
| typedef slip::RegularVector3dField3d < short, double > | RegularVector3dField3d_s |
| short alias More... | |
| typedef slip::RegularVector3dField3d < unsigned short, double > | RegularVector3dField3d_us |
| unsigned long alias More... | |
| typedef slip::RegularVector3dField3d < int, double > | RegularVector3dField3d_i |
| int alias More... | |
| typedef slip::RegularVector3dField3d < unsigned int, double > | RegularVector3dField3d_ui |
| unsigned int alias More... | |
| typedef slip::RegularVector3dField3d < char, double > | RegularVector3dField3d_c |
| char alias More... | |
| typedef slip::RegularVector3dField3d < unsigned char, double > | RegularVector3dField3d_uc |
| unsigned char alias More... | |
| typedef slip::Signal< double > | Signal_d |
| double alias More... | |
| typedef slip::Signal< float > | Signal_f |
| float alias More... | |
| typedef slip::Signal< long > | Signal_l |
| long alias More... | |
| typedef slip::Signal< unsigned long > | Signal_ul |
| unsigned long alias More... | |
| typedef slip::Signal< short > | Signal_s |
| short alias More... | |
| typedef slip::Signal< unsigned short > | Signal_us |
| unsigned long alias More... | |
| typedef slip::Signal< int > | Signal_i |
| int alias More... | |
| typedef slip::Signal< unsigned int > | Signal_ui |
| unsigned int alias More... | |
| typedef slip::Signal< char > | Signal_c |
| char alias More... | |
| typedef slip::Signal< unsigned char > | Signal_uc |
| unsigned char alias More... | |
| typedef slip::Vector< double > | Vector_d |
| double alias More... | |
| typedef slip::Vector< float > | Vector_f |
| float alias More... | |
| typedef slip::Vector< long > | Vector_l |
| long alias More... | |
| typedef slip::Vector< unsigned long > | Vector_ul |
| unsigned long alias More... | |
| typedef slip::Vector< short > | Vector_s |
| short alias More... | |
| typedef slip::Vector< unsigned short > | Vector_us |
| unsigned long alias More... | |
| typedef slip::Vector< int > | Vector_i |
| int alias More... | |
| typedef slip::Vector< unsigned int > | Vector_ui |
| unsigned int alias More... | |
| typedef slip::Vector< char > | Vector_c |
| char alias More... | |
| typedef slip::Vector< unsigned char > | Vector_uc |
| unsigned char alias More... | |
| typedef slip::Vector2d< double > | Vector2d_d |
| double alias More... | |
| typedef slip::Vector2d< float > | Vector2d_f |
| float alias More... | |
| typedef slip::Vector2d< long > | Vector2d_l |
| long alias More... | |
| typedef slip::Vector2d < unsigned long > | Vector2d_ul |
| unsigned long alias More... | |
| typedef slip::Vector2d< short > | Vector2d_s |
| short alias More... | |
| typedef slip::Vector2d < unsigned short > | Vector2d_us |
| unsigned long alias More... | |
| typedef slip::Vector2d< int > | Vector2d_i |
| int alias More... | |
| typedef slip::Vector2d < unsigned int > | Vector2d_ui |
| unsigned int alias More... | |
| typedef slip::Vector2d< char > | Vector2d_c |
| char alias More... | |
| typedef slip::Vector2d < unsigned char > | Vector2d_uc |
| unsigned char alias More... | |
| typedef slip::Vector3d< double > | Vector3d_d |
| double alias More... | |
| typedef slip::Vector3d< float > | Vector3d_f |
| float alias More... | |
| typedef slip::Vector3d< long > | Vector3d_l |
| long alias More... | |
| typedef slip::Vector3d < unsigned long > | Vector3d_ul |
| unsigned long alias More... | |
| typedef slip::Vector3d< short > | Vector3d_s |
| short alias More... | |
| typedef slip::Vector3d < unsigned short > | Vector3d_us |
| unsigned long alias More... | |
| typedef slip::Vector3d< int > | Vector3d_i |
| int alias More... | |
| typedef slip::Vector3d < unsigned int > | Vector3d_ui |
| unsigned int alias More... | |
| typedef slip::Vector3d< char > | Vector3d_c |
| char alias More... | |
| typedef slip::Vector3d < unsigned char > | Vector3d_uc |
| unsigned char alias More... | |
| typedef slip::Vector4d< double > | Vector4d_d |
| double alias More... | |
| typedef slip::Vector4d< float > | Vector4d_f |
| float alias More... | |
| typedef slip::Vector4d< long > | Vector4d_l |
| long alias More... | |
| typedef slip::Vector4d < unsigned long > | Vector4d_ul |
| unsigned long alias More... | |
| typedef slip::Vector4d< short > | Vector4d_s |
| short alias More... | |
| typedef slip::Vector4d < unsigned short > | Vector4d_us |
| unsigned long alias More... | |
| typedef slip::Vector4d< int > | Vector4d_i |
| int alias More... | |
| typedef slip::Vector4d < unsigned int > | Vector4d_ui |
| unsigned int alias More... | |
| typedef slip::Vector4d< char > | Vector4d_c |
| char alias More... | |
| typedef slip::Vector4d < unsigned char > | Vector4d_uc |
| unsigned char alias More... | |
| typedef slip::Volume< double > | Volume_d |
| double alias More... | |
| typedef slip::Volume< float > | Volume_f |
| float alias More... | |
| typedef slip::Volume< long > | Volume_l |
| long alias More... | |
| typedef slip::Volume< unsigned long > | Volume_ul |
| unsigned long alias More... | |
| typedef slip::Volume< short > | Volume_s |
| short alias More... | |
| typedef slip::Volume< unsigned short > | Volume_us |
| unsigned long alias More... | |
| typedef slip::Volume< int > | Volume_i |
| int alias More... | |
| typedef slip::Volume< unsigned int > | Volume_ui |
| unsigned int alias More... | |
| typedef slip::Volume< char > | Volume_c |
| char alias More... | |
| typedef slip::Volume< unsigned char > | Volume_uc |
| unsigned char alias More... | |
Functions | |
| template<typename _II > | |
| void | fill_border (_II first, _II last, std::size_t b_size=1, const typename std::iterator_traits< _II >::value_type &value=typename std::iterator_traits< _II >::value_type()) |
| Fills the border of the range [first,last) with value. More... | |
| template<typename _II > | |
| void | update_border (_II first, _II last, const slip::BORDER_TREATMENT border, const std::size_t b_size=1) |
| Updates the border of the range [first,last) according to b_size and border condition: border. More... | |
| template<typename _II , typename _OI > | |
| void | add_border (_II first, _II last, _OI out_first, _OI out_last, const slip::BORDER_TREATMENT border, const std::size_t b_size=1) |
| Adds the border of the range [first,last) according to the border condtion border and the border size b_size. More... | |
| template<typename Container1 , typename Container2 > | |
| void | add_border1d (const Container1 &in, const slip::BORDER_TREATMENT border_type, Container2 &out, const std::size_t border_size=1) |
| Adds the border at a 1d container according to the border condition border and the border size b_size. More... | |
| template<typename Container2d1 , typename Container2d2 > | |
| void | add_border2d (const Container2d1 &in, const slip::BORDER_TREATMENT border_type, Container2d2 &out, const std::size_t border_size=1) |
| Adds the border at a 2d container according to the border condition border and the border size b_size. More... | |
| template<typename Container3d1 , typename Container3d2 > | |
| void | add_border3d (const Container3d1 &in, const slip::BORDER_TREATMENT border_type, Container3d2 &out, const std::size_t border_size=1) |
| Adds the border at a 3d container according to the border condition border and the border size b_size. More... | |
| template<typename Container4d1 , typename Container4d2 > | |
| void | add_border4d (const Container4d1 &in, const slip::BORDER_TREATMENT border_type, Container4d2 &out, const std::size_t border_size=1) |
| Adds the border at a 4d container according to the border condition border and the border size b_size. More... | |
| template<class Matrix1 , class Matrix2 , class Matrix3 > | |
| int | rq_decomp (const Matrix1 &A, Matrix2 &R, Matrix3 &Q) |
| Computes the RQ decomposition of a matrix. More... | |
| template<typename Type > | |
| void | getpars_DLT (const slip::Matrix< Type > &P, slip::Matrix< Type > &Mat) |
| Get calibration parameters using the DLT. More... | |
| template<typename Type > | |
| void | getpars_DLT_norm (const slip::Matrix< Type > &P, slip::Matrix< Type > &Mat) |
| Get calibration parameters using the DLT. More... | |
| template<typename Type > | |
| void | getpars_Faugeras (const slip::Matrix< Type > &P, slip::Matrix< Type > &Mat) |
| Get calibration parameters using the Faugeras-Algorithm. More... | |
| template<typename Type > | |
| void | getpars_SoloffUV (const slip::Matrix< Type > &P, slip::MultivariatePolynomial< Type, 3 > &Pol_x, slip::MultivariatePolynomial< Type, 3 > &Pol_y) |
| Get calibration parameters using a polynomial fit (computation "by hand") More... | |
| template<typename Type > | |
| void | getpars_SoloffXY (const slip::Matrix< Type > &P, slip::MultivariatePolynomial< Type, 3 > &Pol_x, slip::MultivariatePolynomial< Type, 3 > &Pol_y) |
| Get calibration parameters using a polynomial fit (computation "by hand") More... | |
| template<typename Type > | |
| int | decompose_RQ (const slip::Matrix< Type > &M, slip::Matrix< Type > &K, slip::Matrix< Type > &R, slip::Vector3d< Type > &c) |
| RQ-Decomposition 3x4-Matrix into internal and external parameters. More... | |
| template<typename Type > | |
| int | decompose_direct (const slip::Matrix< Type > &M, slip::Matrix< Type > &K, slip::Matrix< Type > &R, slip::Vector3d< Type > &c) |
| Direct-Decomposition a 3x4-Matrix into internal and external parameters. More... | |
| template<typename Type > | |
| slip::Point2d< Type > | invert_distortion_model (const slip::Point2d< Type > &pd, const slip::Vector< Type > &p) |
| Inverts distortion model using the Newton-method. More... | |
| template<typename Real > | |
| Real | fCieLab (const Real x) |
| int | conj (const int arg) |
| unsigned | conj (const unsigned arg) |
| long | conj (const long arg) |
| short | conj (const short arg) |
| char | conj (const char arg) |
| float | conj (const float arg) |
| double | conj (const double arg) |
| long double | conj (const long double arg) |
| template<typename T > | |
| std::complex< T > | conj (const std::complex< T > &arg) |
| template<typename _II , typename _OI > | |
| void | copy (_II first, _II last, _OI output_first) |
| Copy algorithm optimized for slip iterators. More... | |
| template<typename Real > | |
| Real | minmod (const Real gplus, const Real gminus) |
| template<typename Real > | |
| Real | max_brockett_maragos_plus (const Real gplus, const Real gminus) |
| template<typename Real > | |
| Real | max_brockett_maragos_minus (const Real gplus, const Real gminus) |
| template<typename Real > | |
| Real | osher_sethian_plus (const Real gplus, const Real gminus) |
| template<typename Real > | |
| Real | osher_sethian_minus (const Real gplus, const Real gminus) |
| template<typename InputIterator , typename OutputIterator , typename UnaryOperation > | |
| void | change_dynamic (InputIterator first, InputIterator last, OutputIterator result, UnaryOperation dynamic_fun) |
| Changes the dynamic of a container. More... | |
| template<typename InputIterator , typename OutputIterator , typename MaskIterator , typename UnaryOperation > | |
| void | change_dynamic_mask (InputIterator first, InputIterator last, MaskIterator mask_first, OutputIterator result, UnaryOperation dynamic_fun, typename std::iterator_traits< MaskIterator >::value_type value=typename std::iterator_traits< MaskIterator >::value_type(1)) |
| Changes the dynamic of a container according to a mask sequence. More... | |
| template<typename InputIterator , typename OutputIterator , typename UnaryOperation , typename Predicate > | |
| void | change_dynamic_if (InputIterator first, InputIterator last, OutputIterator result, Predicate pred, UnaryOperation dynamic_fun) |
| Changes the dynamic of a container according to a predicate. More... | |
| template<typename InputIterator , typename OutputIterator > | |
| void | change_dynamic_01 (InputIterator first, InputIterator last, OutputIterator result, slip::NORMALIZATION_FUNCTION fun) |
| Changes the dynamic of a container. More... | |
| template<class RandomAccessIterator , class InnerProduct > | |
| void | gram_schmidt_normalization (RandomAccessIterator init_base_first, RandomAccessIterator init_base_end, RandomAccessIterator ortho_base_first, RandomAccessIterator ortho_base_end, InnerProduct inner_prod) |
| Gram-Schmidt orthonormalization algorithm. More... | |
| template<class RandomAccessIterator , class InnerProduct > | |
| void | modified_gram_schmidt_normalization (RandomAccessIterator init_base_first, RandomAccessIterator init_base_end, RandomAccessIterator ortho_base_first, RandomAccessIterator ortho_base_end, InnerProduct inner_prod) |
| Modified Gram-Schmidt orthonormalization algorithm. More... | |
| template<class RandomAccessIterator , class InnerProduct > | |
| void | gram_schmidt_orthogonalization (RandomAccessIterator init_base_first, RandomAccessIterator init_base_end, RandomAccessIterator ortho_base_first, RandomAccessIterator ortho_base_end, InnerProduct inner_prod) |
| Gram-Schmidt orthogonalization algorithm. More... | |
| template<class RandomAccessIterator , class InnerProduct > | |
| void | modified_gram_schmidt_orthogonalization (RandomAccessIterator init_base_first, RandomAccessIterator init_base_end, RandomAccessIterator ortho_base_first, RandomAccessIterator ortho_base_end, InnerProduct inner_prod) |
| Modified Gram-Schmidt orthogonalization algorithm. More... | |
| template<typename MatrixIterator1 , typename MatrixIterator2 , typename MatrixIterator3 > | |
| void | modified_gram_schmidt (MatrixIterator1 A_up, MatrixIterator1 A_bot, MatrixIterator2 Q_up, MatrixIterator2 Q_bot, MatrixIterator3 R_up, MatrixIterator3 R_bot) |
| Modified Gram-Schmidt orthogonalization algorithm on a matrix. More... | |
| template<class RandomAccessIterator , class RandomAccessIterator2d , class InnerProduct > | |
| void | gram_matrix (RandomAccessIterator init_base_first, RandomAccessIterator init_base_end, RandomAccessIterator2d matrix_upper_left, RandomAccessIterator2d matrix_bottom_right, InnerProduct inner_prod) |
| Compute the Gram matrix from a base. More... | |
| template<typename InputIterator , typename RandomAccessIterator > | |
| void | histogram (InputIterator first, InputIterator last, RandomAccessIterator histo_first, RandomAccessIterator histo_last, typename std::iterator_traits< InputIterator >::value_type minval, typename std::iterator_traits< InputIterator >::value_type maxval, typename std::iterator_traits< InputIterator >::value_type step=1) |
| Simple histogram algorithm (uniform step) More... | |
| template<typename InputIterator , typename RandomAccessIterator , typename MaskIterator > | |
| void | histogram_mask (InputIterator first, InputIterator last, MaskIterator mask_first, RandomAccessIterator histo_first, RandomAccessIterator histo_last, typename std::iterator_traits< InputIterator >::value_type minval, typename std::iterator_traits< InputIterator >::value_type maxval, typename std::iterator_traits< InputIterator >::value_type step=1, typename std::iterator_traits< MaskIterator >::value_type value=typename std::iterator_traits< MaskIterator >::value_type(1)) |
| Simple histogram algorithm (uniform step) according to a mask sequence. More... | |
| template<typename InputIterator , typename RandomAccessIterator , typename Predicate > | |
| void | histogram_if (InputIterator first, InputIterator last, RandomAccessIterator histo_first, RandomAccessIterator histo_last, Predicate pred, typename std::iterator_traits< InputIterator >::value_type minval, typename std::iterator_traits< InputIterator >::value_type maxval, typename std::iterator_traits< InputIterator >::value_type step=1) |
| Simple histogram algorithm (uniform step) according to a predicate. More... | |
| template<typename InputIterator , typename InputIterator2 , typename OutputIterator > | |
| void | real_histogram (InputIterator first, InputIterator last, InputIterator2 stepfirst, InputIterator2 steplast, OutputIterator result) |
| Complex histogram algorithm (variable step) More... | |
| template<typename RandomAccessIterator1 , typename RandomAccessIterator2 > | |
| void | cumulative_histogram (RandomAccessIterator1 histo_first, RandomAccessIterator1 histo_last, RandomAccessIterator2 cum_histo_first, RandomAccessIterator2 cum_histo_last) |
| Computes the cumulative histogram from a histogram. More... | |
| template<typename T , typename RandomAccessIterator > | |
| T | LM_chi2 (RandomAccessIterator first, RandomAccessIterator last) |
| Computes Chi2 for Lebvenberg Marquardt algorithm. More... | |
| template<typename Function , typename Real , typename DerivativeFunction > | |
| void | marquardt (Function &fun, DerivativeFunction &df, slip::Vector< Real > &par, slip::Vector< Real > &r, Real &calchi2, const int maxiter=10000, const Real eps=static_cast< Real >(1e-6)) |
| Optimization of function using the Levenberg-Marquardt algorithm. More... | |
| template<class Matrix1 , class Vector1 , class Matrix2 > | |
| void | hermitian_eigen (const Matrix1 &A, Vector1 &EigenValues, Matrix2 &EigenVectors) |
| Eigen Values Computation of an hermitian semi-definite positive matrix. More... | |
| template<class Matrix1 , class Vector1 > | |
| void | eigen (const Matrix1 &A, Vector1 &E, bool sort=false) |
| Eigen Values Computation for non symmetric matrix. More... | |
| template<class Matrix1 > | |
| slip::lin_alg_traits< typename Matrix1::value_type > ::value_type | spectral_radius (const Matrix1 &A) |
Spectral radius of a matrix 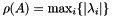 . More... . More... | |
| template<class Matrix1 , class Matrix2 > | |
| void | balance (Matrix1 &A, Matrix2 &D) |
applies a diagonal similarity transform to the square matrix A to make the rows and columns as close in norm as possible. Balancing may reduce the 1-norm of the matrix, and improves the accuracy of the computed eigenvalues and/or eigenvectors. To avoid round-off errors, balance scales A with powers of 2. A is replaced by the balanced matrix which has the same eigenvalues and singular values : 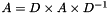 More... More... | |
| template<typename MatrixIterator1 , typename MatrixIterator2 , typename MatrixIterator3 > | |
| void | gram_schmidt_qr (MatrixIterator1 A_up, MatrixIterator1 A_bot, MatrixIterator2 Q_up, MatrixIterator2 Q_bot, MatrixIterator3 R_up, MatrixIterator3 R_bot, const typename slip::lin_alg_traits< typename MatrixIterator1::value_type >::value_type tol) |
| (modified) Gram-Schmidt qr decomposition. More... | |
| template<typename Matrix1 , typename Matrix2 , typename Matrix3 > | |
| void | gram_schmidt_qr (const Matrix1 &A, Matrix2 &Q, Matrix3 &R, const typename slip::lin_alg_traits< typename Matrix1::value_type >::value_type tol) |
| (modified) Gram-Schmidt qr decomposition. More... | |
| template<typename Matrix1 , typename Vector > | |
| void | householder_qr (Matrix1 &M, Vector &V0) |
| in place Householder QR decomposition M = QR
Q is a rotation matrix and R is an upper triangular matrix More... | |
| template<typename Matrix1 , typename Matrix2 , typename Matrix3 > | |
| void | householder_qr (const Matrix1 &M, Matrix2 &Q, Matrix3 &R) |
| Computes the QR decomposition of a matrix M :
Q is a rotation matrix and R is an upper triangular matrix. More... | |
| template<typename MatrixIterator > | |
| std::size_t | subdiag_smaller_elem (MatrixIterator A_up, MatrixIterator A_bot, typename slip::lin_alg_traits< typename std::iterator_traits< MatrixIterator >::value_type >::value_type precision) |
| find the smaller non null (according to the precision) subdiagonal element of a matrix More... | |
| template<typename MatrixIterator1 , typename MatrixIterator2 , typename MatrixIterator3 > | |
| void | Schur_factorization_2by2 (MatrixIterator1 A_up, MatrixIterator1 A_bot, MatrixIterator2 Z_up, MatrixIterator2 Z_bot, MatrixIterator3 D_up, MatrixIterator3 D_bot) |
Computes the Schur factorization of a real 2-by-2 2d container : 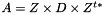
where : More... | |
| template<class Matrix , typename VectorIterator > | |
| void | MatrixHouseholder (Matrix &H, VectorIterator V_begin, VectorIterator V_end) |
| Computes the Householder matrix of a vector V :
If V is an householder vector of a matrix M then | |
| template<class Vector , typename MatrixIterator > | |
| void | VectorHouseholder (Vector &V, MatrixIterator M_up, MatrixIterator M_bot) |
| Computes a Householder vector V from a matrix M :
with
. More... | |
| template<typename HessenbergMatrix , typename Matrix > | |
| bool | Francis_QR_Step (HessenbergMatrix &H, Matrix &Z, slip::Box2d< int > box, bool compute_z) |
| Computes the Francis QR Step used in the Schur decomposition
Algorithm 7.5-1 in "Matrix Computations", Golub and Van Loan. More... | |
| template<class HessenbergMatrix , class Vector , class Matrix > | |
| void | Francis_Schur_standardize (HessenbergMatrix &H, Vector &Eig, Matrix &Z, slip::Box2d< int > b22, bool compute_z) |
| Converts a 2-by-2 diagonal block of H in the Schur form, normalizes H and extract the associated eigenvalues.
Algorithm 7.5-1 in "Matrix Computations", Golub and Van Loan. More... | |
| template<class HessenbergMatrix , class Vector , class Matrix > | |
| bool | Francis_Schur_decomp (HessenbergMatrix &H, Vector &Eig, Matrix &Z, slip::Box2d< int > &box, typename slip::lin_alg_traits< typename HessenbergMatrix::value_type >::value_type precision, bool compute_Z) |
| computes the Schur decomposition of a square Hessenberg Matrix and copy the eigenvalues in the Eig vector :
Algorithm 7.5-2 in "Matrix Computations", Golub and Van Loan. More... | |
| template<class Matrix1 , class Matrix2 , class Vector , class Matrix3 > | |
| bool | schur (const Matrix1 &M, Matrix2 &H, Matrix3 &Z, Vector &Eig, bool compute_Z, typename slip::lin_alg_traits< typename Matrix1::value_type >::value_type precision=typename slip::lin_alg_traits< typename Matrix1::value_type >::value_type(1.0E-12)) |
| computes the shur decomposition of a square Matrix and copy the eigenvalues in the Eig vector:
Algorithm 7.5-2 in "Matrix Computations", Golub and Van Loan. More... | |
| template<class Matrix1 , class Matrix2 > | |
| bool | Sylvester_solve (const Matrix1 &S, slip::Box2d< int > &b11, slip::Box2d< int > &b22, double &g, Matrix2 &X) |
Solve the sylvester equation (from Z.Bai and J.W. Demmel article : -On Swapping Diagonal Blocks in Real Schur Form- In Linear Algebra and its Applications 186:73-95(1993)) : 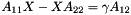 . More... . More... | |
| template<typename T > | |
| bool | is_real (const T &val) |
| Test if an element is real. More... | |
| template<typename T > | |
| bool | is_complex (const T &val) |
| Test if an element is complex. More... | |
| template<typename T > | |
| slip::lin_alg_traits< T > ::value_type | epsilon () |
| Returns the epsilon value of a real or a complex. More... | |
| template<typename T > | |
| T | sign (T a) |
| Computes the sign of a. More... | |
| template<typename Real > | |
| Real | pythagore (const Real &x, const Real &y) |
Computes 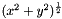 without destructive underflow or overflow. More... without destructive underflow or overflow. More... | |
| template<int N, typename T > | |
| T | nth_power (T x) |
Computes the nth power of an element 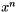 . More... . More... | |
| template<typename T , typename Integer > | |
| T | power (T x, Integer N) |
| function to compute. More... | |
| template<typename Value_T , typename InputIterator > | |
| Value_T | L22_norm (InputIterator first, InputIterator last) |
Computes the L22 norm ( 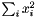 ) of a range. More... ) of a range. More... | |
| template<typename Value_T , typename InputIterator , typename MaskIterator > | |
| Value_T | L22_norm_mask (InputIterator first, InputIterator last, MaskIterator mask_first, typename std::iterator_traits< MaskIterator >::value_type value=typename std::iterator_traits< MaskIterator >::value_type(1)) |
Computes the L22 norm 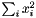 of a range according to a mask sequence. More... of a range according to a mask sequence. More... | |
| template<typename Value_T , typename InputIterator , typename Predicate > | |
| Value_T | L22_norm_if (InputIterator first, InputIterator last, Predicate pred) |
Computes the L22 norm 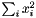 a range according to a Predicate. More... a range according to a Predicate. More... | |
| template<typename Value_T , typename InputIterator > | |
| Value_T | L2_norm (InputIterator first, InputIterator last) |
Computes the L2 norm 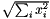 of a range. More... of a range. More... | |
| template<typename Value_T , typename InputIterator , typename MaskIterator > | |
| Value_T | L2_norm_mask (InputIterator first, InputIterator last, MaskIterator mask_first, typename std::iterator_traits< MaskIterator >::value_type value=typename std::iterator_traits< MaskIterator >::value_type(1)) |
Computes the Euclidean norm 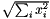 of a range according to a mask sequence. More... of a range according to a mask sequence. More... | |
| template<typename Value_T , typename InputIterator , typename Predicate > | |
| Value_T | L2_norm_if (InputIterator first, InputIterator last, Predicate pred) |
Computes the Euclidean norm 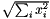 a range according to a Predicate. More... a range according to a Predicate. More... | |
| template<typename Value_T , typename InputIterator > | |
| Value_T | Euclidean_norm (InputIterator first, InputIterator last) |
Computes the Euclidean norm 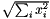 of a range. More... of a range. More... | |
| template<typename Value_T , typename InputIterator , typename MaskIterator > | |
| Value_T | Euclidean_norm_mask (InputIterator first, InputIterator last, MaskIterator mask_first, typename std::iterator_traits< MaskIterator >::value_type value=typename std::iterator_traits< MaskIterator >::value_type(1)) |
Computes the Euclidean norm 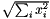 of a range according to a mask sequence. More... of a range according to a mask sequence. More... | |
| template<typename Value_T , typename InputIterator , typename Predicate > | |
| Value_T | Euclidean_norm_if (InputIterator first, InputIterator last, Predicate pred) |
Computes the Euclidean norm 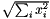 a range according to a Predicate. More... a range according to a Predicate. More... | |
| template<typename Value_T , typename InputIterator > | |
| Value_T | L1_norm (InputIterator first, InputIterator last) |
Computes the L1 norm 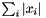 of a range. More... of a range. More... | |
| template<typename Value_T , typename InputIterator , typename MaskIterator > | |
| Value_T | L1_norm_mask (InputIterator first, InputIterator last, MaskIterator mask_first, typename std::iterator_traits< MaskIterator >::value_type value=typename std::iterator_traits< MaskIterator >::value_type(1)) |
Computes the L1 norm 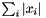 of a range according to a mask sequence. More... of a range according to a mask sequence. More... | |
| template<typename Value_T , typename InputIterator , typename Predicate > | |
| Value_T | L1_norm_if (InputIterator first, InputIterator last, Predicate pred) |
Computes the L1 norm 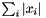 a range according to a Predicate. More... a range according to a Predicate. More... | |
| template<typename Value_T , typename InputIterator > | |
| Value_T | infinite_norm (InputIterator first, InputIterator last) |
Computes the infinite norm 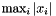 of a range. More... of a range. More... | |
| template<typename Value_T , typename InputIterator , typename MaskIterator > | |
| Value_T | infinite_norm_mask (InputIterator first, InputIterator last, MaskIterator mask_first, typename std::iterator_traits< MaskIterator >::value_type value=typename std::iterator_traits< MaskIterator >::value_type(1)) |
Computes the infinite norm 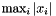 of a range according to a mask sequence. More... of a range according to a mask sequence. More... | |
| template<typename Value_T , typename InputIterator , typename Predicate > | |
| Value_T | infinite_norm_if (InputIterator first, InputIterator last, Predicate pred) |
Computes the infinite norm 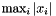 a range according to a Predicate. More... a range according to a Predicate. More... | |
| template<class OutputMatrix > | |
| void | pca_uniform_metric (OutputMatrix &metric) |
| Get uniform metric for PCA computation. More... | |
| template<class Matrix , class OutputMatrix > | |
| void | pca_adaptative_metric (const Matrix &data, OutputMatrix &metric) |
| Get adaptative metric for PCA computation. More... | |
| template<class Matrix , class OutputMatrix > | |
| void | pca_center_data (const Matrix &data, OutputMatrix ¢erdata, const bool normalize_data=false) |
| Get uniform metric for PCA computation. More... | |
| template<class Matrix , class Matrix2 , class OutputMatrix , class OutputVector > | |
| void | pca_computation (const Matrix &data, OutputMatrix &acp, const Matrix2 &metric, OutputVector &eigenval) |
| Compute the PCA (data need to be centered) More... | |
| template<class Matrix , class OutputMatrix > | |
| void | pca_simple_data_reduction_axis (const Matrix &acp, OutputMatrix &result, const std::size_t &nbaxis) |
| Reduce ACP data. More... | |
| template<class Matrix , class Matrix2 , class OutputMatrix > | |
| void | pca_data_reduction (const Matrix &data, const Matrix2 &metric, OutputMatrix &result, const std::size_t &nbaxis, const bool normalize_data=false) |
| Data reduction using ACP. More... | |
| template<class Matrix , class Matrix2 , class OutputMatrix > | |
| void | pca_data_reduction (const Matrix &data, const Matrix2 &metric, OutputMatrix &result, const bool normalize_data=false) |
| Data reduction using ACP. More... | |
| template<typename Integer , typename InputIterator > | |
| Integer | cardinal (InputIterator first, InputIterator last) |
| Computes the cardinal or the number of elements of a range. More... | |
| template<typename Value_T , typename InputIterator > | |
| Value_T | mean (InputIterator first, InputIterator last) |
| Computes the mean value of a range
. More... | |
| template<typename Value_T , typename InputIterator > | |
| Value_T | weighted_mean (InputIterator first, InputIterator last, InputIterator w_first, InputIterator w_last) |
| Computes the weighted mean value of a range:
. More... | |
| template<typename T , int N, typename InputIterator > | |
| T | nth_moment (InputIterator first, InputIterator last, T mean) |
| Computes the nth moment of a range
. More... | |
| template<typename T , typename InputIterator , typename InputIterator2 > | |
| T | covariance (InputIterator first, InputIterator last, InputIterator2 first2, T mean1, T mean2) |
| Computes the covariance of a two sequences
. More... | |
| template<typename T , typename InputIterator , typename InputIterator2 > | |
| T | unbiased_covariance (InputIterator first, InputIterator last, InputIterator2 first2, T mean1, T mean2) |
| Computes the unbiased covariance of a two sequences
. More... | |
| template<typename T , typename InputIterator > | |
| T | variance (InputIterator first, InputIterator last, T mean) |
| Computes the variance of a range
. More... | |
| template<typename T , typename InputIterator > | |
| T | unbiased_variance (InputIterator first, InputIterator last, T mean) |
| Computes the unbiased variance of a range
. More... | |
| template<typename T , typename InputIterator > | |
| T | std_dev (InputIterator first, InputIterator last, T mean) |
| Computes the standard deviation of a range
. More... | |
| template<typename T , typename InputIterator > | |
| T | unbiased_std_dev (InputIterator first, InputIterator last, T mean) |
| Computes the unbiased standard deviation of a range
. More... | |
| template<typename T , typename InputIterator > | |
| T | kurtosis (InputIterator first, InputIterator last, T mean) |
| Computes the kurtosis of a range
A high kurtosis distribution has a sharper peak and longer, fatter tails, while a low kurtosis distribution has a more rounded peak and shorter thinner tails. Here are some common value of kurtosis for unimodal and symmetric densities: More... | |
| template<typename T , typename InputIterator > | |
| T | unbiased_kurtosis (InputIterator first, InputIterator last, T mean) |
| Computes the unbiased kurtosis of a range
A high kurtosis distribution has a sharper peak and longer, fatter tails, while a low kurtosis distribution has a more rounded peak and shorter thinner tails. More... | |
| template<typename T , typename InputIterator > | |
| T | skewness (InputIterator first, InputIterator last, T mean) |
| Computes the skewness of a range
skewness is a measure of the asymmetry of the probability distribution of a real-valued random variable. More... | |
| template<typename T , typename InputIterator > | |
| T | unbiased_skewness (InputIterator first, InputIterator last, T mean) |
| Computes the unbiased skewness of a range
skewness is a measure of the asymmetry of the probability distribution of a real-valued random variable. More... | |
| template<typename T , typename InputIterator > | |
| T | rms (InputIterator first, InputIterator last) |
| Computes the root mean square (rms) value of a range
. More... | |
| template<typename InputIterator > | |
| std::iterator_traits < InputIterator >::value_type | median_from_sorted_data (InputIterator first, InputIterator last) |
| Computes the median value from a sorted range: returns *(first + (last - first) / 2) More... | |
| template<typename RandomAccessIterator , typename Size > | |
| std::iterator_traits < RandomAccessIterator > ::value_type | median_from_sorted_data_n (RandomAccessIterator first, Size n) |
| Computes the median value from a sorted range: returns *(first + n/2). More... | |
| template<typename RandomAccessIterator , typename Size > | |
| std::iterator_traits < RandomAccessIterator > ::value_type | median_from_data_n (RandomAccessIterator first, RandomAccessIterator last, Size n) |
| Computes the median value from a non sorted range. More... | |
| template<typename RandomAccessIterator , typename Size , typename StrictWeakOrdering > | |
| std::iterator_traits < RandomAccessIterator > ::value_type | median_from_data_n (RandomAccessIterator first, RandomAccessIterator last, Size n, StrictWeakOrdering comp) |
| Computes the median value from a non sorted range. More... | |
| template<typename RandomAccessIterator > | |
| std::iterator_traits < RandomAccessIterator > ::value_type | median (RandomAccessIterator first, RandomAccessIterator last) |
| Computes the median value from a range. More... | |
| template<typename RandomAccessIterator , typename StrictWeakOrdering > | |
| std::iterator_traits < RandomAccessIterator > ::value_type | median (RandomAccessIterator first, RandomAccessIterator last, StrictWeakOrdering comp) |
| Computes the median value from a range. More... | |
| template<typename RandomAccessIterator , typename SizeType > | |
| std::iterator_traits < RandomAccessIterator > ::value_type | median_n (RandomAccessIterator first, RandomAccessIterator last, SizeType n) |
| Computes the median value from a range of size n. More... | |
| template<typename RandomAccessIterator , typename SizeType , typename StrictWeakOrdering > | |
| std::iterator_traits < RandomAccessIterator > ::value_type | median_n (RandomAccessIterator first, RandomAccessIterator last, SizeType n, StrictWeakOrdering comp) |
| Computes the median value from a range of size n. More... | |
| template<typename RandomAccessIterator > | |
| std::iterator_traits < RandomAccessIterator > ::value_type | first_quartile (RandomAccessIterator first, RandomAccessIterator last) |
| Computes the first quartile value from a non sorted range. More... | |
| template<typename RandomAccessIterator > | |
| std::iterator_traits < RandomAccessIterator > ::value_type | third_quartile (RandomAccessIterator first, RandomAccessIterator last) |
| Computes the third quartile value from a non sorted range. More... | |
| template<typename ForwardIterator > | |
| void | n_max_elements (ForwardIterator first, ForwardIterator last, std::vector< ForwardIterator > &max, const std::size_t n=1) |
| finds the n largest elements in the range [first, last). More... | |
| template<typename ForwardIterator > | |
| void | n_min_elements (ForwardIterator first, ForwardIterator last, std::vector< ForwardIterator > &min, const std::size_t n=1) |
| finds the n smallest elements in the range [first, last). More... | |
| template<typename RandomAccessIterator , typename RandomAccessIterator2 > | |
| void | center (RandomAccessIterator first, RandomAccessIterator last, RandomAccessIterator2 out_first) |
| Substracts its mean to a range. More... | |
| template<typename RandomAccessIterator , typename RandomAccessIterator2 > | |
| void | studentize (RandomAccessIterator first, RandomAccessIterator last, RandomAccessIterator2 out_first) |
| Substracts its mean to a range and divide it by its standard deviation. More... | |
| template<typename Value_T , typename InputIterator , typename MaskIterator > | |
| Value_T | mean_mask (InputIterator first, InputIterator last, MaskIterator mask_first, typename std::iterator_traits< MaskIterator >::value_type value=typename std::iterator_traits< MaskIterator >::value_type(1)) |
| Computes the mean value of a range over a mask
. More... | |
| template<typename T , int N, typename InputIterator , typename MaskIterator > | |
| T | nth_moment_mask (InputIterator first, InputIterator last, MaskIterator mask_first, T mean, typename std::iterator_traits< MaskIterator >::value_type value=typename std::iterator_traits< MaskIterator >::value_type(1)) |
| Computes the nth moment of a range over a mask
. More... | |
| template<typename T , typename InputIterator , typename InputIterator2 , typename MaskIterator > | |
| T | covariance_mask (InputIterator first, InputIterator last, InputIterator2 first2, MaskIterator mask_first, T mean1, T mean2, typename std::iterator_traits< MaskIterator >::value_type value=typename std::iterator_traits< MaskIterator >::value_type(1)) |
| Computes the covariance of a two sequences over a mask
. More... | |
| template<typename T , typename InputIterator , typename InputIterator2 , typename MaskIterator > | |
| T | unbiased_covariance_mask (InputIterator first, InputIterator last, InputIterator2 first2, MaskIterator mask_first, T mean1, T mean2, typename std::iterator_traits< MaskIterator >::value_type value=typename std::iterator_traits< MaskIterator >::value_type(1)) |
| Computes the unbiased covariance of a two sequences over a mask
. More... | |
| template<typename T , typename InputIterator , typename MaskIterator > | |
| T | variance_mask (InputIterator first, InputIterator last, MaskIterator mask_first, T mean, typename std::iterator_traits< MaskIterator >::value_type value=typename std::iterator_traits< MaskIterator >::value_type(1)) |
| Computes the variance of a range over a mask
. More... | |
| template<typename T , typename InputIterator , typename MaskIterator > | |
| T | unbiased_variance_mask (InputIterator first, InputIterator last, MaskIterator mask_first, T mean, typename std::iterator_traits< MaskIterator >::value_type value=typename std::iterator_traits< MaskIterator >::value_type(1)) |
| Computes the unbiased variance of a range over a mask
. More... | |
| template<typename T , typename InputIterator , typename MaskIterator > | |
| T | std_dev_mask (InputIterator first, InputIterator last, MaskIterator mask_first, T mean, typename std::iterator_traits< MaskIterator >::value_type value=typename std::iterator_traits< MaskIterator >::value_type(1)) |
| Computes the standard deviation of a range over a mask
. More... | |
| template<typename T , typename InputIterator , typename MaskIterator > | |
| T | unbiased_std_dev_mask (InputIterator first, InputIterator last, MaskIterator mask_first, T mean, typename std::iterator_traits< MaskIterator >::value_type value=typename std::iterator_traits< MaskIterator >::value_type(1)) |
| Computes the unbiased standard deviation of a range over a mask
. More... | |
| template<typename T , typename InputIterator , typename MaskIterator > | |
| T | kurtosis_mask (InputIterator first, InputIterator last, MaskIterator mask_first, T mean, typename std::iterator_traits< MaskIterator >::value_type value=typename std::iterator_traits< MaskIterator >::value_type(1)) |
| Computes the kurtosis of a range over a mask
A high kurtosis distribution has a sharper peak and longer, fatter tails, while a low kurtosis distribution has a more rounded peak and shorter thinner tails. Here are some common value of kurtosis for unimodal and symmetric densities: More... | |
| template<typename T , typename InputIterator , typename MaskIterator > | |
| T | unbiased_kurtosis_mask (InputIterator first, InputIterator last, MaskIterator mask_first, T mean, typename std::iterator_traits< MaskIterator >::value_type value=typename std::iterator_traits< MaskIterator >::value_type(1)) |
| Computes the unbiased kurtosis of a range over a mask
A high kurtosis distribution has a sharper peak and longer, fatter tails, while a low kurtosis distribution has a more rounded peak and shorter thinner tails. More... | |
| template<typename T , typename InputIterator , typename MaskIterator > | |
| T | skewness_mask (InputIterator first, InputIterator last, MaskIterator mask_first, T mean, typename std::iterator_traits< MaskIterator >::value_type value=typename std::iterator_traits< MaskIterator >::value_type(1)) |
| Computes the skewness of a range over a mask
skewness is a measure of the asymmetry of the probability distribution of a real-valued random variable. More... | |
| template<typename T , typename InputIterator , typename MaskIterator > | |
| T | unbiased_skewness_mask (InputIterator first, InputIterator last, MaskIterator mask_first, T mean, typename std::iterator_traits< MaskIterator >::value_type value=typename std::iterator_traits< MaskIterator >::value_type(1)) |
| Computes the unbiased skewness of a range over a mask
skewness is a measure of the asymmetry of the probability distribution of a real-valued random variable. More... | |
| template<typename T , typename InputIterator , typename MaskIterator > | |
| T | rms_mask (InputIterator first, InputIterator last, MaskIterator mask_first, typename std::iterator_traits< MaskIterator >::value_type value=typename std::iterator_traits< MaskIterator >::value_type(1)) |
| Computes the root mean square (rms) value of a range over a mask
. More... | |
| template<typename Integer , typename MaskIterator > | |
| Integer | cardinal_mask (MaskIterator mask_first, MaskIterator mask_last, typename std::iterator_traits< MaskIterator >::value_type value=typename std::iterator_traits< MaskIterator >::value_type(1)) |
| Computes the cardinal or the number of elements of a mask range. More... | |
| template<typename InputIterator , typename MaskIterator > | |
| std::iterator_traits < InputIterator >::value_type | median_from_sorted_data_mask (InputIterator first, InputIterator last, MaskIterator mask_first, typename std::iterator_traits< MaskIterator >::value_type value=typename std::iterator_traits< MaskIterator >::value_type(1)) |
| Computes the median value from a sorted range over a mask. More... | |
| template<typename InputIterator , typename MaskIterator > | |
| std::iterator_traits < InputIterator >::value_type | median_mask (InputIterator first, InputIterator last, MaskIterator mask_first, typename std::iterator_traits< MaskIterator >::value_type value=typename std::iterator_traits< MaskIterator >::value_type(1)) |
| Computes the median value from a non sorted range over a mask. More... | |
| template<typename InputIterator , typename MaskIterator > | |
| std::iterator_traits < InputIterator >::value_type | first_quartile_mask (InputIterator first, InputIterator last, MaskIterator mask_first, typename std::iterator_traits< MaskIterator >::value_type value=typename std::iterator_traits< MaskIterator >::value_type(1)) |
| Computes the first quartile value from a non sorted range over a mask. More... | |
| template<typename InputIterator , typename MaskIterator > | |
| std::iterator_traits < InputIterator >::value_type | third_quartile_mask (InputIterator first, InputIterator last, MaskIterator mask_first, typename std::iterator_traits< MaskIterator >::value_type value=typename std::iterator_traits< MaskIterator >::value_type(1)) |
| Computes the third quartile value from a non sorted range over a mask. More... | |
| template<typename InputIterator , typename MaskIterator , typename OutputIterator > | |
| void | center_mask (InputIterator first, InputIterator last, MaskIterator mask_first, OutputIterator out_first, typename std::iterator_traits< MaskIterator >::value_type value=typename std::iterator_traits< MaskIterator >::value_type(1)) |
| Substracts its mean to a range according a mask. More... | |
| template<typename InputIterator , typename MaskIterator , typename OutputIterator > | |
| void | studentize_mask (InputIterator first, InputIterator last, MaskIterator mask_first, OutputIterator out_first, typename std::iterator_traits< MaskIterator >::value_type value=typename std::iterator_traits< MaskIterator >::value_type(1)) |
| Substracts its mean to a range and divide it by its standard deviation according a mask. More... | |
| template<typename Integer , typename InputIterator , typename Predicate > | |
| Integer | cardinal_if (InputIterator first, InputIterator last, Predicate pred) |
| Computes the cardinal or the number of elements of a range using a predicate. More... | |
| template<typename Value_T , typename InputIterator , typename Predicate > | |
| Value_T | mean_if (InputIterator first, InputIterator last, Predicate pred) |
| Computes the mean value of a range using a predicate
. More... | |
| template<typename T , int N, typename InputIterator , typename Predicate > | |
| T | nth_moment_if (InputIterator first, InputIterator last, T mean, Predicate pred) |
| Computes the nth moment of a range using a predicate
. More... | |
| template<typename T , typename InputIterator , typename InputIterator2 , typename Predicate > | |
| T | covariance_if (InputIterator first, InputIterator last, InputIterator2 first2, T mean1, T mean2, Predicate pred) |
| Computes the covariance of a two sequences using a predicate on the first one
. More... | |
| template<typename T , typename InputIterator , typename InputIterator2 , typename Predicate > | |
| T | unbiased_covariance_if (InputIterator first, InputIterator last, InputIterator2 first2, T mean1, T mean2, Predicate pred) |
| Computes the unbiased covariance of a two sequences using a predicate on the first one
. More... | |
| template<typename T , typename InputIterator , typename Predicate > | |
| T | variance_if (InputIterator first, InputIterator last, T mean, Predicate pred) |
| Computes the variance of a range using a predicate
. More... | |
| template<typename T , typename InputIterator , typename Predicate > | |
| T | unbiased_variance_if (InputIterator first, InputIterator last, T mean, Predicate pred) |
| Computes the unbiased variance of a range using a predicate
. More... | |
| template<typename T , typename InputIterator , typename Predicate > | |
| T | std_dev_if (InputIterator first, InputIterator last, T mean, Predicate pred) |
| Computes the standard deviation of a range using a predicate
. More... | |
| template<typename T , typename InputIterator , typename Predicate > | |
| T | unbiased_std_dev_if (InputIterator first, InputIterator last, T mean, Predicate pred) |
| Computes the unbiased standard deviation of a range using a predicate
. More... | |
| template<typename T , typename InputIterator , typename Predicate > | |
| T | kurtosis_if (InputIterator first, InputIterator last, T mean, Predicate pred) |
| Computes the kurtosis of a range using a predicate
A high kurtosis distribution has a sharper peak and longer, fatter tails, while a low kurtosis distribution has a more rounded peak and shorter thinner tails. Here are some common value of kurtosis for unimodal and symmetric densities: More... | |
| template<typename T , typename InputIterator , typename Predicate > | |
| T | unbiased_kurtosis_if (InputIterator first, InputIterator last, T mean, Predicate pred) |
| Computes the unbiased kurtosis of a range using a predicate
A high kurtosis distribution has a sharper peak and longer, fatter tails, while a low kurtosis distribution has a more rounded peak and shorter thinner tails. More... | |
| template<typename T , typename InputIterator , typename Predicate > | |
| T | skewness_if (InputIterator first, InputIterator last, T mean, Predicate pred) |
| Computes the skewness of a range using a predicate
skewness is a measure of the asymmetry of the probability distribution of a real-valued random variable. More... | |
| template<typename T , typename InputIterator , typename Predicate > | |
| T | unbiased_skewness_if (InputIterator first, InputIterator last, T mean, Predicate pred) |
| Computes the unbiased skewness of a range using a predicate
skewness is a measure of the asymmetry of the probability distribution of a real-valued random variable. More... | |
| template<typename T , typename InputIterator , typename Predicate > | |
| T | rms_if (InputIterator first, InputIterator last, Predicate pred) |
| Computes the root mean square (rms) value of a range using a predicate
. More... | |
| template<typename InputIterator , typename Predicate > | |
| std::iterator_traits < InputIterator >::value_type | median_from_sorted_data_if (InputIterator first, InputIterator last, Predicate pred) |
| Computes the median value from a sorted range using a predicate. More... | |
| template<typename InputIterator , typename Predicate > | |
| std::iterator_traits < InputIterator >::value_type | median_if (InputIterator first, InputIterator last, Predicate pred) |
| Computes the median value from a non sorted range using a predicate. More... | |
| template<typename InputIterator , typename Predicate > | |
| std::iterator_traits < InputIterator >::value_type | first_quartile_if (InputIterator first, InputIterator last, Predicate pred) |
| Computes the first quartile value from a non sorted range using a predicate. More... | |
| template<typename InputIterator , typename Predicate > | |
| std::iterator_traits < InputIterator >::value_type | third_quartile_if (InputIterator first, InputIterator last, Predicate pred) |
| Computes the third quartile value from a non sorted range using a predicate. More... | |
| template<typename InputIterator , typename Predicate , typename OutputIterator > | |
| void | center_if (InputIterator first, InputIterator last, Predicate pred, OutputIterator out_first) |
| Substracts its mean to a range using a predicate. More... | |
| template<typename InputIterator , typename Predicate , typename OutputIterator > | |
| void | studentize_if (InputIterator first, InputIterator last, Predicate pred, OutputIterator out_first) |
| Substracts its mean to a range and divide it by its standard deviation using a predicate. More... | |
| template<typename InputIterator , typename T > | |
| void | statistics (InputIterator first, InputIterator last, slip::Statistics< T > &statistic) |
| compute all statistics of a range More... | |
| template<typename InputIterator , typename T > | |
| void | unbiased_statistics (InputIterator first, InputIterator last, slip::Statistics< T > &statistic) |
| compute all unbiased statistics of a range More... | |
| template<typename InputIterator , typename T , typename MaskIterator > | |
| void | statistics_mask (InputIterator first, InputIterator last, MaskIterator mask_first, slip::Statistics< T > &statistic, typename std::iterator_traits< MaskIterator >::value_type value=typename std::iterator_traits< MaskIterator >::value_type(1)) |
| compute all statistics of a range according to a mask range. More... | |
| template<typename InputIterator , typename T , typename MaskIterator > | |
| void | unbiased_statistics_mask (InputIterator first, InputIterator last, MaskIterator mask_first, slip::Statistics< T > &statistic, typename std::iterator_traits< MaskIterator >::value_type value=typename std::iterator_traits< MaskIterator >::value_type(1)) |
| compute all unbiased statistics of a range according to a mask range. More... | |
| template<typename InputIterator , typename T , typename Predicate > | |
| void | statistics_if (InputIterator first, InputIterator last, slip::Statistics< T > &statistic, Predicate pred) |
| compute all statistics of a range according to a preidcate. More... | |
| template<typename InputIterator , typename T , typename Predicate > | |
| void | unbiased_statistics_if (InputIterator first, InputIterator last, slip::Statistics< T > &statistic, Predicate pred) |
| compute all unbiased statistics of a range according to a preidcate. More... | |
| template<typename _InputIterator1 , typename _InputIterator2 , typename _MaskIterator , typename _Tp > | |
| _Tp | inner_product_mask (_InputIterator1 first1, _InputIterator1 last1, _MaskIterator mask_first, _InputIterator2 first2, _Tp init, typename std::iterator_traits< _MaskIterator >::value_type value=typename std::iterator_traits< _MaskIterator >::value_type(1)) |
| Compute inner product of two ranges according to a mask range. More... | |
| template<typename _InputIterator1 , typename _InputIterator2 , typename _MaskIterator , typename _Tp , typename _BinaryOperation1 , typename _BinaryOperation2 > | |
| _Tp | inner_product_mask (_InputIterator1 first1, _InputIterator1 last1, _MaskIterator mask_first, _InputIterator2 first2, _Tp init, _BinaryOperation1 binary_op1, _BinaryOperation2 binary_op2, typename std::iterator_traits< _MaskIterator >::value_type value=typename std::iterator_traits< _MaskIterator >::value_type(1)) |
| Compute inner product of two ranges according to a mask range. More... | |
| template<typename _InputIterator1 , typename _InputIterator2 , typename _Predicate , typename _Tp > | |
| _Tp | inner_product_if (_InputIterator1 first1, _InputIterator1 last1, _InputIterator2 first2, _Tp init, _Predicate pred) |
| Compute inner product of two ranges according to a Predicate. More... | |
| template<typename _InputIterator1 , typename _InputIterator2 , typename _Tp , typename _BinaryOperation1 , typename _BinaryOperation2 , typename _Predicate > | |
| _Tp | inner_product_if (_InputIterator1 first1, _InputIterator1 last1, _InputIterator2 first2, _Tp init, _BinaryOperation1 binary_op1, _BinaryOperation2 binary_op2, _Predicate pred) |
| Compute inner product of two ranges according to a Predicate. More... | |
| template<typename T > | |
| int | get_tecplot_type () |
| Convert the type of a variable to an integer using Tecplot conventions. More... | |
| int | plt_get_order (std::ifstream &fp) |
| Read a binary tecplot file, move the stream pointer and return header informations. More... | |
| int | plt_get_order (const std::string &file_path_name) |
| Read a binary tecplot file, move the stream pointer and return header informations. More... | |
| int | plt_get_file_type (std::ifstream &fp) |
| Read a binary tecplot file, move the stream pointer and return header informations. More... | |
| int | plt_get_file_type (const std::string &file_path_name) |
| Read a binary tecplot file, move the stream pointer and return header informations. More... | |
| void | plt_read_header (std::ifstream &fp, int &NbVars, int &NbZones, int &K, int &I, int &J, std::string &title, std::string &zonename, std::vector< std::string > &varnames, double &SolTime, int NumZone=1) |
| Read a binary tecplot file, move the stream pointer and return header informations. More... | |
| void | plt_read_header (std::ifstream &fp, int &NbVars, int &NbZones, int &K, int &I, int &J, int NumZone=1) |
| Read a binary tecplot file and return header informations. More... | |
| void | plt_read_header (const std::string &file_path_name, int &NbVars, int &NbZones, int &K, int &I, int &J, int NumZone=1) |
| Read a binary tecplot file and return header informations. More... | |
| void | plt_read_header (const std::string &file_path_name, int &NbVars, int &NbZones, int &K, int &I, int &J, double &SolTime, int NumZone=1) |
| Read a binary tecplot file and return header informations. More... | |
| void | plt_read_header (const std::string &file_path_name, int &NbVars, int &NbZones, int &K, int &I, int &J, std::string &title, std::string &zonename, std::vector< std::string > &varnames, double &SolTime, int NumZone=1) |
| Read a binary tecplot file and return header informations. More... | |
| template<typename Container2d > | |
| void | plt_to_Array2d (const std::string &file_path_name, Container2d ®, const int zone_loaded=1) |
| Read a binary tecplot file and put the data in a 2d container. More... | |
| template<typename RegularVector3dField3d > | |
| void | plt_to_RegularVector3dField3d (const std::string &file_path_name, RegularVector3dField3d ®, std::string &title, std::string &zonename, std::vector< std::string > &varnames, const int zone_loaded=1) |
| Read a slip::RegularVector3dField3d from a binary tecplot file. More... | |
| template<typename RegularVector3dField3d > | |
| void | plt_to_RegularVector3dField3d (const std::string &file_path_name, RegularVector3dField3d ®, const int zone_loaded=1) |
| Read a slip::RegularVector3dField3d from a binary tecplot file. More... | |
| bool | compareTwoRows3D (double *rowA, double *rowB) |
| Comparator used to sort an Array2d. More... | |
| template<typename RegularVector3dField3d > | |
| void | generic_plt_to_RegularVector3dField3d (const std::string &file_path_name, RegularVector3dField3d ®, std::string &title, std::string &zonename, std::vector< std::string > &varnames, const int zone_loaded=1) |
| Read a slip::RegularVector3dField3d from a binary tecplot file even if data are not properly sorted. This function is slower than plt_to_RegularVector3dField3d(). More... | |
| template<typename RegularVector3dField3d > | |
| void | generic_plt_to_RegularVector3dField3d (const std::string &file_path_name, RegularVector3dField3d ®, const int zone_loaded=1) |
| Read a slip::RegularVector3dField3d from a binary tecplot file. More... | |
| template<typename RegularVector3dField3d > | |
| void | RegularVector3dField3d_to_plt (const std::string &file_path_name, RegularVector3dField3d ®, std::string title, std::string zone, const double SolTime, std::vector< std::string > varnames=std::vector< std::string >(), const int FileType=0) |
| Write a slip::RegularVector3dField3d to a binary tecplot file. More... | |
| template<typename RegularVector3dField3d > | |
| void | RegularVector3dField3d_to_plt (const std::string &file_path_name, RegularVector3dField3d ®, const int FileType=0) |
| Write a slip::RegularVector3dField3d to a binary tecplot file. More... | |
| template<typename RegularVector3dField3d > | |
| void | RegularVector3dField3d_to_plt (const std::string &file_path_name, RegularVector3dField3d ®, const double SolTime, const int FileType=0) |
| Write a slip::RegularVector3dField3d to a binary tecplot file. More... | |
| template<typename RegularVector3dField3d > | |
| void | RegularVector3dField3d_to_plt (const std::string &file_path_name, RegularVector3dField3d ®, std::string title, std::string zone, const int FileType=0) |
| Write a slip::RegularVector3dField3d to a binary tecplot file. More... | |
| template<typename RegularVector3dField3d > | |
| void | RegularVector3dField3d_to_plt (const std::string &file_path_name, RegularVector3dField3d ®, std::string title, std::string zone, std::vector< std::string > varnames, const int FileType=0) |
| Write a slip::RegularVector3dField3d to a binary tecplot file. More... | |
| template<typename RegularVector2dField2d > | |
| void | plt_to_RegularVector2dField2d (const std::string &file_path_name, RegularVector2dField2d ®, std::string &title, std::string &zonename, std::vector< std::string > &varnames, const int zone_loaded=1) |
| Read a slip::RegularVector2dField2d from a binary tecplot file. More... | |
| template<typename RegularVector2dField2d > | |
| void | plt_to_RegularVector2dField2d (const std::string &file_path_name, RegularVector2dField2d ®, const int zone_loaded=1) |
| Read a slip::RegularVector2dField2d from a binary tecplot file. More... | |
| bool | compareTwoRows2D (double *rowA, double *rowB) |
| Comparator used to sort an Array2d. More... | |
| template<typename RegularVector2dField2d > | |
| void | generic_plt_to_RegularVector2dField2d (const std::string &file_path_name, RegularVector2dField2d ®, std::string &title, std::string &zonename, std::vector< std::string > &varnames, const int zone_loaded=1) |
| Read a slip::RegularVector2dField2d from a binary tecplot file. More... | |
| template<typename RegularVector2dField2d > | |
| void | generic_plt_to_RegularVector2dField2d (const std::string &file_path_name, RegularVector2dField2d ®, const int zone_loaded=1) |
| Read a slip::RegularVector2dField2d from a binary tecplot file. More... | |
| template<typename RegularVector2dField2d > | |
| void | RegularVector2dField2d_to_plt (const std::string &file_path_name, RegularVector2dField2d ®, std::string title, std::string zone, const double SolTime, std::vector< std::string > varnames=std::vector< std::string >(), const int FileType=0) |
| Write a slip::RegularVector2dField2d to a binary tecplot file. More... | |
| template<typename RegularVector2dField2d > | |
| void | RegularVector2dField2d_to_plt (const std::string &file_path_name, RegularVector2dField2d ®, const int FileType=0) |
| Write a slip::RegularVector2dField2d to a binary tecplot file. More... | |
| template<typename RegularVector2dField2d > | |
| void | RegularVector2dField2d_to_plt (const std::string &file_path_name, RegularVector2dField2d ®, const double SolTime, const int FileType=0) |
| Write a slip::RegularVector2dField2d to a binary tecplot file. More... | |
| template<typename RegularVector2dField2d > | |
| void | RegularVector2dField2d_to_plt (const std::string &file_path_name, RegularVector2dField2d ®, std::string title, std::string zone, const int FileType=0) |
| Write a slip::RegularVector2dField2d to a binary tecplot file. More... | |
| template<typename RegularVector2dField2d > | |
| void | RegularVector2dField2d_to_plt (const std::string &file_path_name, RegularVector2dField2d ®, std::string title, std::string zone, std::vector< std::string > varnames, const int FileType=0) |
| Write a slip::RegularVector2dField2d to a binary tecplot file. More... | |
| template<typename InputIterator , typename OutputIterator > | |
| void | binarize (InputIterator first, InputIterator last, OutputIterator result, const typename std::iterator_traits< InputIterator >::value_type &t_value, const typename std::iterator_traits< OutputIterator >::value_type &false_value, const typename std::iterator_traits< OutputIterator >::value_type &true_value) |
| binarize algorithm More... | |
| template<typename InputIterator , typename OutputIterator > | |
| void | threshold (InputIterator first, InputIterator last, OutputIterator result, const typename std::iterator_traits< InputIterator >::value_type &t_value, const typename std::iterator_traits< OutputIterator >::value_type &false_value) |
| threshold algorithm More... | |
| template<typename InputIterator , typename OutputIterator > | |
| void | db_threshold (InputIterator first, InputIterator last, OutputIterator result, const typename std::iterator_traits< InputIterator >::value_type &min_t_value, const typename std::iterator_traits< InputIterator >::value_type &max_t_value, const typename std::iterator_traits< OutputIterator >::value_type &false_value) |
| double-threshold algorithm More... | |
| template<typename InputIterator1 , typename RandomAccessIterator1 , typename RandomAccessIterator2 , typename OutputIterator > | |
| void | multi_threshold (InputIterator1 first, InputIterator1 last, RandomAccessIterator1 first_th, RandomAccessIterator1 last_th, RandomAccessIterator2 first_level, RandomAccessIterator2 last_level, OutputIterator result_first, OutputIterator result_last) |
| multi_threshold algorithm It is equivalent to a quantification J[i] = Level[i] if T[i-1] < I[i] <= T[i] More... | |
| template<typename CoordType , std::size_t DIM> | |
| std::ostream & | operator<< (std::ostream &out, const Box< CoordType, DIM > &b) |
| template<typename T > | |
| ColorHyperVolume< T > | operator+ (const ColorHyperVolume< T > &M1, const ColorHyperVolume< T > &M2) |
| pointwise addition of two ColorHyperVolume More... | |
| template<typename T > | |
| ColorHyperVolume< T > | operator+ (const ColorHyperVolume< T > &M1, const T &val) |
| addition of a scalar to each element of a ColorHyperVolume More... | |
| template<typename T > | |
| ColorHyperVolume< T > | operator+ (const T &val, const ColorHyperVolume< T > &M1) |
| addition of a scalar to each element of a ColorHyperVolume More... | |
| template<typename T > | |
| ColorHyperVolume< T > | operator+ (const ColorHyperVolume< T > &M1, const slip::Color< T > &val) |
| addition of a Color block to each element of a ColorHyperVolume More... | |
| template<typename T > | |
| ColorHyperVolume< T > | operator+ (const slip::Color< T > &val, const ColorHyperVolume< T > &M1) |
| addition of a Color block to each element of a ColorHyperVolume More... | |
| template<typename T > | |
| ColorHyperVolume< T > | operator- (const ColorHyperVolume< T > &M1, const ColorHyperVolume< T > &M2) |
| pointwise subtraction of two ColorHyperVolume More... | |
| template<typename T > | |
| ColorHyperVolume< T > | operator- (const ColorHyperVolume< T > &M1, const T &val) |
| subtraction of a scalar to each element of a ColorHyperVolume More... | |
| template<typename T > | |
| ColorHyperVolume< T > | operator- (const T &val, const ColorHyperVolume< T > &M1) |
| subtraction of a scalar to each element of a ColorHyperVolume More... | |
| template<typename T > | |
| ColorHyperVolume< T > | operator- (const ColorHyperVolume< T > &M1, const slip::Color< T > &val) |
| subtraction of a Color block to each element of a ColorHyperVolume More... | |
| template<typename T > | |
| ColorHyperVolume< T > | operator* (const ColorHyperVolume< T > &M1, const ColorHyperVolume< T > &M2) |
| pointwise multiplication of two ColorHyperVolume More... | |
| template<typename T > | |
| ColorHyperVolume< T > | operator* (const ColorHyperVolume< T > &M1, const T &val) |
| multiplication of a scalar to each element of a ColorHyperVolume More... | |
| template<typename T > | |
| ColorHyperVolume< T > | operator* (const T &val, const ColorHyperVolume< T > &M1) |
| multiplication of a scalar to each element of a ColorHyperVolume More... | |
| template<typename T > | |
| ColorHyperVolume< T > | operator* (const ColorHyperVolume< T > &M1, const slip::Color< T > &val) |
| multiplication of a Color block to each element of a ColorHyperVolume More... | |
| template<typename T > | |
| ColorHyperVolume< T > | operator* (const slip::Color< T > &val, const ColorHyperVolume< T > &M1) |
| multiplication of a Color block to each element of a ColorHyperVolume More... | |
| template<typename T > | |
| ColorHyperVolume< T > | operator/ (const ColorHyperVolume< T > &M1, const ColorHyperVolume< T > &M2) |
| pointwise division of two ColorHyperVolume More... | |
| template<typename T > | |
| ColorHyperVolume< T > | operator/ (const ColorHyperVolume< T > &M1, const T &val) |
| division of a scalar to each element of a ColorHyperVolume More... | |
| template<typename T > | |
| ColorHyperVolume< T > | operator/ (const ColorHyperVolume< T > &M1, const slip::Color< T > &val) |
| division of each element of a ColorHyperVolume by a Color block More... | |
| template<typename T > | |
| ColorImage< T > | operator+ (const ColorImage< T > &M1, const ColorImage< T > &M2) |
| pointwise addition of two ColorImage More... | |
| template<typename T > | |
| ColorImage< T > | operator+ (const ColorImage< T > &M1, const T &val) |
| addition of a scalar to each element of a ColorImage More... | |
| template<typename T > | |
| ColorImage< T > | operator+ (const T &val, const ColorImage< T > &M1) |
| addition of a scalar to each element of a ColorImage More... | |
| template<typename T > | |
| ColorImage< T > | operator- (const ColorImage< T > &M1, const ColorImage< T > &M2) |
| pointwise substraction of two ColorImage More... | |
| template<typename T > | |
| ColorImage< T > | operator- (const ColorImage< T > &M1, const T &val) |
| substraction of a scalar to each element of a ColorImage More... | |
| template<typename T > | |
| ColorImage< T > | operator- (const T &val, const ColorImage< T > &M1) |
| substraction of a scalar to each element of a ColorImage More... | |
| template<typename T > | |
| ColorImage< T > | operator* (const ColorImage< T > &M1, const ColorImage< T > &M2) |
| pointwise multiplication of two ColorImage More... | |
| template<typename T > | |
| ColorImage< T > | operator* (const ColorImage< T > &M1, const T &val) |
| multiplication of a scalar to each element of a ColorImage More... | |
| template<typename T > | |
| ColorImage< T > | operator* (const T &val, const ColorImage< T > &M1) |
| multiplication of a scalar to each element of a ColorImage More... | |
| template<typename T > | |
| ColorImage< T > | operator/ (const ColorImage< T > &M1, const ColorImage< T > &M2) |
| pointwise division of two ColorImage More... | |
| template<typename T > | |
| ColorImage< T > | operator/ (const ColorImage< T > &M1, const T &val) |
| division of a scalar to each element of a ColorImage More... | |
| template<typename T > | |
| ColorImage< T > | operator+ (const ColorImage< T > &M1, const slip::Color< T > &val) |
| template<typename T > | |
| ColorImage< T > | operator+ (const slip::Color< T > &val, const ColorImage< T > &M1) |
| template<typename T > | |
| ColorImage< T > | operator- (const ColorImage< T > &M1, const slip::Color< T > &val) |
| template<typename T > | |
| ColorImage< T > | operator- (const slip::Color< T > &val, const ColorImage< T > &M1) |
| template<typename T > | |
| ColorImage< T > | operator* (const ColorImage< T > &M1, const slip::Color< T > &val) |
| template<typename T > | |
| ColorImage< T > | operator* (const slip::Color< T > &val, const ColorImage< T > &M1) |
| template<typename T > | |
| ColorImage< T > | operator/ (const ColorImage< T > &M1, const slip::Color< T > &val) |
| template<typename T > | |
| ColorVolume< T > | operator+ (const ColorVolume< T > &M1, const ColorVolume< T > &M2) |
| pointwise addition of two ColorVolume More... | |
| template<typename T > | |
| ColorVolume< T > | operator+ (const ColorVolume< T > &M1, const T &val) |
| addition of a scalar to each element of a ColorVolume More... | |
| template<typename T > | |
| ColorVolume< T > | operator+ (const T &val, const ColorVolume< T > &M1) |
| addition of a scalar to each element of a ColorVolume More... | |
| template<typename T > | |
| ColorVolume< T > | operator+ (const ColorVolume< T > &M1, const slip::Color< T > &val) |
| addition of a Color block to each element of a ColorVolume More... | |
| template<typename T > | |
| ColorVolume< T > | operator+ (const slip::Color< T > &val, const ColorVolume< T > &M1) |
| addition of a Color block to each element of a ColorVolume More... | |
| template<typename T > | |
| ColorVolume< T > | operator- (const ColorVolume< T > &M1, const ColorVolume< T > &M2) |
| pointwise subtraction of two ColorVolume More... | |
| template<typename T > | |
| ColorVolume< T > | operator- (const ColorVolume< T > &M1, const T &val) |
| subtraction of a scalar to each element of a ColorVolume More... | |
| template<typename T > | |
| ColorVolume< T > | operator- (const T &val, const ColorVolume< T > &M1) |
| subtraction of a scalar to each element of a ColorVolume More... | |
| template<typename T > | |
| ColorVolume< T > | operator- (const ColorVolume< T > &M1, const slip::Color< T > &val) |
| subtraction of a Color block to each element of a ColorVolume More... | |
| template<typename T > | |
| ColorVolume< T > | operator* (const ColorVolume< T > &M1, const ColorVolume< T > &M2) |
| pointwise multiplication of two ColorVolume More... | |
| template<typename T > | |
| ColorVolume< T > | operator* (const ColorVolume< T > &M1, const T &val) |
| multiplication of a scalar to each element of a ColorVolume More... | |
| template<typename T > | |
| ColorVolume< T > | operator* (const T &val, const ColorVolume< T > &M1) |
| multiplication of a scalar to each element of a ColorVolume More... | |
| template<typename T > | |
| ColorVolume< T > | operator* (const ColorVolume< T > &M1, const slip::Color< T > &val) |
| multiplication of a Color block to each element of a ColorVolume More... | |
| template<typename T > | |
| ColorVolume< T > | operator* (const slip::Color< T > &val, const ColorVolume< T > &M1) |
| multiplication of a Color block to each element of a ColorVolume More... | |
| template<typename T > | |
| ColorVolume< T > | operator/ (const ColorVolume< T > &M1, const ColorVolume< T > &M2) |
| pointwise division of two ColorVolume More... | |
| template<typename T > | |
| ColorVolume< T > | operator/ (const ColorVolume< T > &M1, const T &val) |
| division of a scalar to each element of a ColorVolume More... | |
| template<typename T > | |
| ColorVolume< T > | operator/ (const ColorVolume< T > &M1, const slip::Color< T > &val) |
| division of each element of a ColorVolume by a Color block More... | |
| template<typename Container , typename _II > | |
| void | container_cast (Container &cont, _II &first, _II &last) |
| Get the default iterators of a SLIP container. More... | |
| template<typename Container , typename _II > | |
| void | reverse_container_cast (Container &cont, _II &first, _II &last) |
| Get the reverse default iterators of a SLIP container. More... | |
| template<typename Container , typename _II > | |
| void | container_castR (Container &cont, _II &first, _II &last) |
| Get the reverse default iterators of a SLIP container. More... | |
| template<typename Type > | |
| std::ostream & | operator<< (std::ostream &out, const DistortionCamera< Type > &c) |
| template<typename CoordType , std::size_t DIM> | |
| std::ostream & | operator<< (std::ostream &out, const DPoint< CoordType, DIM > &p) |
| template<typename Block > | |
| std::ostream & | operator<< (std::ostream &out, const slip::GenericMultiComponent2d< Block > &a) |
| template<typename Block > | |
| bool | operator== (const slip::GenericMultiComponent2d< Block > &x, const slip::GenericMultiComponent2d< Block > &y) |
| template<typename Block > | |
| bool | operator!= (const slip::GenericMultiComponent2d< Block > &x, const slip::GenericMultiComponent2d< Block > &y) |
| template<typename Block > | |
| std::ostream & | operator<< (std::ostream &out, const slip::GenericMultiComponent3d< Block > &a) |
| template<typename Block > | |
| bool | operator== (const slip::GenericMultiComponent3d< Block > &x, const slip::GenericMultiComponent3d< Block > &y) |
| template<typename Block > | |
| bool | operator!= (const slip::GenericMultiComponent3d< Block > &x, const slip::GenericMultiComponent3d< Block > &y) |
| template<typename Block > | |
| std::ostream & | operator<< (std::ostream &out, const GenericMultiComponent4d< Block > &a) |
| template<typename Block > | |
| bool | operator== (const GenericMultiComponent4d< Block > &x, const GenericMultiComponent4d< Block > &y) |
| template<typename Block > | |
| bool | operator!= (const GenericMultiComponent4d< Block > &x, const GenericMultiComponent4d< Block > &y) |
| template<typename T > | |
| std::ostream & | operator<< (std::ostream &out, const slip::GrayscaleImage< T > &a) |
| template<typename T > | |
| T & | min (const GrayscaleImage< T > &M1) |
| Returns the min element of a GrayscaleImage. More... | |
| template<typename T > | |
| T & | max (const GrayscaleImage< T > &M1) |
| Returns the max element of a GrayscaleImage. More... | |
| template<typename T > | |
| std::ostream & | operator<< (std::ostream &out, const slip::HyperVolume< T > &a) |
| template<typename T > | |
| HyperVolume< T > | operator+ (const HyperVolume< T > &M1, const HyperVolume< T > &M2) |
| pointwise addition of two HyperVolume More... | |
| template<typename T > | |
| HyperVolume< T > | operator+ (const HyperVolume< T > &M1, const T &val) |
| addition of a scalar to each element of a HyperVolume More... | |
| template<typename T > | |
| HyperVolume< T > | operator+ (const T &val, const HyperVolume< T > &M1) |
| addition of a scalar to each element of a HyperVolume More... | |
| template<typename T > | |
| HyperVolume< T > | operator- (const HyperVolume< T > &M1, const HyperVolume< T > &M2) |
| pointwise substraction of two HyperVolume More... | |
| template<typename T > | |
| HyperVolume< T > | operator- (const HyperVolume< T > &M1, const T &val) |
| substraction of a scalar to each element of a HyperVolume More... | |
| template<typename T > | |
| HyperVolume< T > | operator- (const T &val, const HyperVolume< T > &M1) |
| substraction of a scalar to each element of a HyperVolume More... | |
| template<typename T > | |
| HyperVolume< T > | operator* (const HyperVolume< T > &M1, const HyperVolume< T > &M2) |
| pointwise multiplication of two HyperVolume More... | |
| template<typename T > | |
| HyperVolume< T > | operator* (const HyperVolume< T > &M1, const T &val) |
| multiplication of a scalar to each element of a HyperVolume More... | |
| template<typename T > | |
| HyperVolume< T > | operator* (const T &val, const HyperVolume< T > &M1) |
| multiplication of a scalar to each element of a HyperVolume More... | |
| template<typename T > | |
| HyperVolume< T > | operator/ (const HyperVolume< T > &M1, const HyperVolume< T > &M2) |
| pointwise division of two HyperVolume More... | |
| template<typename T > | |
| HyperVolume< T > | operator/ (const HyperVolume< T > &M1, const T &val) |
| division of a scalar to each element of a HyperVolume More... | |
| template<typename T > | |
| T & | min (const HyperVolume< T > &M1) |
| template<typename T > | |
| T & | max (const HyperVolume< T > &M1) |
| template<typename T > | |
| HyperVolume< T > | abs (const HyperVolume< T > &M) |
| template<typename T > | |
| HyperVolume< T > | sqrt (const HyperVolume< T > &M) |
| template<typename T > | |
| HyperVolume< T > | cos (const HyperVolume< T > &M) |
| template<typename T > | |
| HyperVolume< T > | acos (const HyperVolume< T > &M) |
| template<typename T > | |
| HyperVolume< T > | sin (const HyperVolume< T > &M) |
| template<typename T > | |
| HyperVolume< T > | asin (const HyperVolume< T > &M) |
| template<typename T > | |
| HyperVolume< T > | tan (const HyperVolume< T > &M) |
| template<typename T > | |
| HyperVolume< T > | atan (const HyperVolume< T > &M) |
| template<typename T > | |
| HyperVolume< T > | exp (const HyperVolume< T > &M) |
| template<typename T > | |
| HyperVolume< T > | log (const HyperVolume< T > &M) |
| template<typename T > | |
| HyperVolume< T > | cosh (const HyperVolume< T > &M) |
| template<typename T > | |
| HyperVolume< T > | sinh (const HyperVolume< T > &M) |
| template<typename T > | |
| HyperVolume< T > | tanh (const HyperVolume< T > &M) |
| template<typename T > | |
| HyperVolume< T > | log10 (const HyperVolume< T > &M) |
| template<typename T , std::size_t N> | |
| std::ostream & | operator<< (std::ostream &out, const kvector< T, N > &b) |
| template<typename T , std::size_t N> | |
| bool | operator== (const kvector< T, N > &x, const kvector< T, N > &y) |
| template<typename T , std::size_t N> | |
| bool | operator!= (const kvector< T, N > &x, const kvector< T, N > &y) |
| template<typename T , std::size_t N> | |
| bool | operator< (const kvector< T, N > &x, const kvector< T, N > &y) |
| template<typename T , std::size_t N> | |
| bool | operator> (const kvector< T, N > &x, const kvector< T, N > &y) |
| template<typename T , std::size_t N> | |
| bool | operator<= (const kvector< T, N > &x, const kvector< T, N > &y) |
| template<typename T , std::size_t N> | |
| bool | operator>= (const kvector< T, N > &x, const kvector< T, N > &y) |
| template<typename T , std::size_t N> | |
| kvector< T, N > | operator+ (const kvector< T, N > &V1, const kvector< T, N > &V2) |
| pointwise addition of two kvector More... | |
| template<typename T , std::size_t N> | |
| kvector< T, N > | operator+ (const kvector< T, N > &V, const T &val) |
| addition of a scalar to each element of a kvector More... | |
| template<typename T , std::size_t N> | |
| kvector< T, N > | operator+ (const T &val, const kvector< T, N > &V) |
| addition of a scalar to each element of a kvector More... | |
| template<typename T , std::size_t N> | |
| kvector< T, N > | operator- (const kvector< T, N > &V1, const kvector< T, N > &V2) |
| pointwise substraction of two kvector More... | |
| template<typename T , std::size_t N> | |
| kvector< T, N > | operator- (const kvector< T, N > &V, const T &val) |
| substraction of a scalar to each element of a kvector More... | |
| template<typename T , std::size_t N> | |
| kvector< T, N > | operator- (const T &val, const kvector< T, N > &V) |
| substraction of a scalar to each element of a kvector More... | |
| template<typename T , std::size_t N> | |
| kvector< T, N > | operator* (const kvector< T, N > &V1, const kvector< T, N > &V2) |
| pointwise multiplication of two kvector More... | |
| template<typename T , std::size_t N> | |
| kvector< T, N > | operator* (const kvector< T, N > &V, const T &val) |
| multiplication of a scalar to each element of a kvector More... | |
| template<typename T , std::size_t N> | |
| kvector< T, N > | operator* (const T &val, const kvector< T, N > &V) |
| multiplication of a scalar to each element of a kvector More... | |
| template<typename T , std::size_t N> | |
| kvector< T, N > | operator/ (const kvector< T, N > &V1, const kvector< T, N > &V2) |
| pointwise division of two kvector More... | |
| template<typename T , std::size_t N> | |
| kvector< T, N > | operator/ (const kvector< T, N > &V, const T &val) |
| division of a scalar to each element of a kvector More... | |
| template<typename T , std::size_t N> | |
| T & | min (kvector< T, N > &V1) |
| template<typename T , std::size_t N> | |
| T & | max (kvector< T, N > &V1) |
| template<typename T , std::size_t N> | |
| kvector< typename slip::lin_alg_traits< T > ::value_type, N > | abs (const kvector< T, N > &V) |
| template<typename T , std::size_t N> | |
| kvector< T, N > | sqrt (const kvector< T, N > &V) |
| template<typename T , std::size_t N> | |
| kvector< T, N > | cos (const kvector< T, N > &V) |
| template<std::size_t N> | |
| kvector< float, N > | acos (const kvector< float, N > &V) |
| template<std::size_t N> | |
| kvector< double, N > | acos (const kvector< double, N > &V) |
| template<std::size_t N> | |
| kvector< long double, N > | acos (const kvector< long double, N > &V) |
| template<typename T , std::size_t N> | |
| kvector< T, N > | sin (const kvector< T, N > &V) |
| template<std::size_t N> | |
| kvector< float, N > | asin (const kvector< float, N > &V) |
| template<std::size_t N> | |
| kvector< double, N > | asin (const kvector< double, N > &V) |
| template<std::size_t N> | |
| kvector< long double, N > | asin (const kvector< long double, N > &V) |
| template<typename T , std::size_t N> | |
| kvector< T, N > | tan (const kvector< T, N > &V) |
| template<std::size_t N> | |
| kvector< float, N > | atan (const kvector< float, N > &V) |
| template<std::size_t N> | |
| kvector< double, N > | atan (const kvector< double, N > &V) |
| template<std::size_t N> | |
| kvector< long double, N > | atan (const kvector< long double, N > &V) |
| template<typename T , std::size_t N> | |
| kvector< T, N > | exp (const kvector< T, N > &V) |
| template<typename T , std::size_t N> | |
| kvector< T, N > | log (const kvector< T, N > &V) |
| template<typename T , std::size_t N> | |
| kvector< T, N > | cosh (const kvector< T, N > &V) |
| template<typename T , std::size_t N> | |
| kvector< T, N > | sinh (const kvector< T, N > &V) |
| template<typename T , std::size_t N> | |
| kvector< T, N > | tanh (const kvector< T, N > &V) |
| template<typename T , std::size_t N> | |
| kvector< T, N > | log10 (const kvector< T, N > &V) |
| template<typename T > | |
| std::ostream & | operator<< (std::ostream &out, const slip::Matrix< T > &a) |
| template<typename T > | |
| T & | min (const Matrix< T > &M1) |
| template<typename T > | |
| T & | max (const Matrix< T > &M1) |
| template<typename T > | |
| Matrix< typename slip::lin_alg_traits< T > ::value_type > | abs (const Matrix< T > &M) |
| template<typename T > | |
| Matrix< T > | sqrt (const Matrix< T > &M) |
| template<typename T > | |
| Matrix< T > | cos (const Matrix< T > &M) |
| Matrix< float > | acos (const Matrix< float > &M) |
| Matrix< double > | acos (const Matrix< double > &M) |
| Matrix< long double > | acos (const Matrix< long double > &M) |
| template<typename T > | |
| Matrix< T > | sin (const Matrix< T > &M) |
| Matrix< float > | asin (const Matrix< float > &M) |
| Matrix< double > | asin (const Matrix< double > &M) |
| Matrix< long double > | asin (const Matrix< long double > &M) |
| template<typename T > | |
| Matrix< T > | tan (const Matrix< T > &M) |
| Matrix< float > | atan (const Matrix< float > &M) |
| Matrix< double > | atan (const Matrix< double > &M) |
| Matrix< long double > | atan (const Matrix< long double > &M) |
| template<typename T > | |
| Matrix< T > | exp (const Matrix< T > &M) |
| template<typename T > | |
| Matrix< T > | log (const Matrix< T > &M) |
| template<typename T > | |
| Matrix< T > | cosh (const Matrix< T > &M) |
| template<typename T > | |
| Matrix< T > | sinh (const Matrix< T > &M) |
| template<typename T > | |
| Matrix< T > | tanh (const Matrix< T > &M) |
| template<typename T > | |
| Matrix< T > | log10 (const Matrix< T > &M) |
| template<typename T > | |
| T & | min (const Matrix3d< T > &M1) |
| template<typename T > | |
| T & | max (const Matrix3d< T > &M1) |
| template<typename T > | |
| Matrix3d< T > | abs (const Matrix3d< T > &M) |
| template<typename T > | |
| Matrix3d< T > | sqrt (const Matrix3d< T > &M) |
| template<typename T > | |
| Matrix3d< T > | cos (const Matrix3d< T > &M) |
| template<typename T > | |
| Matrix3d< T > | acos (const Matrix3d< T > &M) |
| template<typename T > | |
| Matrix3d< T > | sin (const Matrix3d< T > &M) |
| template<typename T > | |
| Matrix3d< T > | asin (const Matrix3d< T > &M) |
| template<typename T > | |
| Matrix3d< T > | tan (const Matrix3d< T > &M) |
| template<typename T > | |
| Matrix3d< T > | atan (const Matrix3d< T > &M) |
| template<typename T > | |
| Matrix3d< T > | exp (const Matrix3d< T > &M) |
| template<typename T > | |
| Matrix3d< T > | log (const Matrix3d< T > &M) |
| template<typename T > | |
| Matrix3d< T > | cosh (const Matrix3d< T > &M) |
| template<typename T > | |
| Matrix3d< T > | sinh (const Matrix3d< T > &M) |
| template<typename T > | |
| Matrix3d< T > | tanh (const Matrix3d< T > &M) |
| template<typename T > | |
| Matrix3d< T > | log10 (const Matrix3d< T > &M) |
| template<typename T > | |
| T & | min (const Matrix4d< T > &M1) |
| template<typename T > | |
| T & | max (const Matrix4d< T > &M1) |
| template<typename T > | |
| Matrix4d< T > | abs (const Matrix4d< T > &M) |
| template<typename T > | |
| Matrix4d< T > | sqrt (const Matrix4d< T > &M) |
| template<typename T > | |
| Matrix4d< T > | cos (const Matrix4d< T > &M) |
| template<typename T > | |
| Matrix4d< T > | acos (const Matrix4d< T > &M) |
| template<typename T > | |
| Matrix4d< T > | sin (const Matrix4d< T > &M) |
| template<typename T > | |
| Matrix4d< T > | asin (const Matrix4d< T > &M) |
| template<typename T > | |
| Matrix4d< T > | tan (const Matrix4d< T > &M) |
| template<typename T > | |
| Matrix4d< T > | atan (const Matrix4d< T > &M) |
| template<typename T > | |
| Matrix4d< T > | exp (const Matrix4d< T > &M) |
| template<typename T > | |
| Matrix4d< T > | log (const Matrix4d< T > &M) |
| template<typename T > | |
| Matrix4d< T > | cosh (const Matrix4d< T > &M) |
| template<typename T > | |
| Matrix4d< T > | sinh (const Matrix4d< T > &M) |
| template<typename T > | |
| Matrix4d< T > | tanh (const Matrix4d< T > &M) |
| template<typename T > | |
| Matrix4d< T > | log10 (const Matrix4d< T > &M) |
| template<std::size_t DIM> | |
| std::ostream & | operator<< (std::ostream &out, const Monomial< DIM > &m) |
| template<typename T , std::size_t DIM> | |
| std::ostream & | operator<< (std::ostream &out, const MultivariatePolynomial< T, DIM > &v) |
| template<std::size_t DIM> | |
| std::ostream & | operator<< (std::ostream &out, const MultivariatePolynomial< std::complex< double >, DIM > &m) |
| template<std::size_t DIM> | |
| std::ostream & | operator<< (std::ostream &out, const MultivariatePolynomial< std::complex< float >, DIM > &m) |
| template<std::size_t DIM> | |
| std::ostream & | operator<< (std::ostream &out, const MultivariatePolynomial< std::complex< long double >, DIM > &m) |
| template<typename T , std::size_t DIM> | |
| MultivariatePolynomial< T, DIM > | operator+ (const MultivariatePolynomial< T, DIM > &P1, const MultivariatePolynomial< T, DIM > &P2) |
| template<typename T , std::size_t DIM> | |
| MultivariatePolynomial< T, DIM > | operator+ (const MultivariatePolynomial< T, DIM > &P1, const T &val) |
| template<typename T , std::size_t DIM> | |
| MultivariatePolynomial< T, DIM > | operator+ (const T &val, const MultivariatePolynomial< T, DIM > &P1) |
| template<typename T , std::size_t DIM> | |
| MultivariatePolynomial< T, DIM > | operator- (const MultivariatePolynomial< T, DIM > &P1, const MultivariatePolynomial< T, DIM > &P2) |
| template<typename T , std::size_t DIM> | |
| MultivariatePolynomial< T, DIM > | operator- (const MultivariatePolynomial< T, DIM > &P1, const T &val) |
| template<typename T , std::size_t DIM> | |
| MultivariatePolynomial< T, DIM > | operator- (const T &val, const MultivariatePolynomial< T, DIM > &P1) |
| template<typename T , std::size_t DIM> | |
| MultivariatePolynomial< T, DIM > | operator* (const MultivariatePolynomial< T, DIM > &P1, const MultivariatePolynomial< T, DIM > &P2) |
| template<typename T , std::size_t DIM> | |
| MultivariatePolynomial< T, DIM > | operator* (const MultivariatePolynomial< T, DIM > &P1, const T &val) |
| template<typename T , std::size_t DIM> | |
| MultivariatePolynomial< T, DIM > | operator* (const T &val, const MultivariatePolynomial< T, DIM > &P1) |
| template<typename T , std::size_t DIM> | |
| MultivariatePolynomial< T, DIM > | operator/ (const MultivariatePolynomial< T, DIM > &P1, const T &val) |
| template<typename Type > | |
| std::ostream & | operator<< (std::ostream &out, const PinholeCamera< Type > &c) |
| template<typename Type > | |
| std::ostream & | operator<< (std::ostream &out, const PinholeDLTCamera< Type > &c) |
| template<typename Type > | |
| std::ostream & | operator<< (std::ostream &out, const PinholeFaugerasCamera< Type > &c) |
| template<typename CoordType , std::size_t DIM> | |
| std::ostream & | operator<< (std::ostream &out, const Point< CoordType, DIM > &p) |
| template<typename T > | |
| std::ostream & | operator<< (std::ostream &out, const Polynomial< T > &v) |
| template<typename Container > | |
| std::ostream & | operator<< (std::ostream &out, const slip::Pyramid< Container > &a) |
| template<typename Container > | |
| bool | operator== (const Pyramid< Container > &x, const Pyramid< Container > &y) |
| template<typename Container > | |
| bool | operator!= (const Pyramid< Container > &x, const Pyramid< Container > &y) |
| template<typename SubType > | |
| std::ostream & | operator<< (std::ostream &out, const Range< SubType > &b) |
| template<typename SubType > | |
| bool | operator== (const Range< SubType > &b1, const Range< SubType > &b2) |
| template<typename SubType > | |
| bool | operator!= (const Range< SubType > &b1, const Range< SubType > &b2) |
| template<typename T , typename GridT > | |
| std::ostream & | operator<< (std::ostream &out, const slip::RegularVector2dField2d< T, GridT > &a) |
| template<typename T , typename GridT > | |
| RegularVector2dField2d< T, GridT > | operator+ (const RegularVector2dField2d< T, GridT > &M1, const T &val) |
| addition of a scalar to each element of a RegularVector2dField2d More... | |
| template<typename T , typename GridT > | |
| RegularVector2dField2d< T, GridT > | operator+ (const T &val, const RegularVector2dField2d< T, GridT > &M1) |
| addition of a scalar to each element of a RegularVector2dField2d More... | |
| template<typename T , typename GridT > | |
| RegularVector2dField2d< T, GridT > | operator- (const RegularVector2dField2d< T, GridT > &M1, const T &val) |
| substraction of a scalar to each element of a RegularVector2dField2d More... | |
| template<typename T , typename GridT > | |
| RegularVector2dField2d< T, GridT > | operator- (const T &val, const RegularVector2dField2d< T, GridT > &M1) |
| substraction of a scalar to each element of a RegularVector2dField2d More... | |
| template<typename T , typename GridT > | |
| RegularVector2dField2d< T, GridT > | operator* (const RegularVector2dField2d< T, GridT > &M1, const T &val) |
| multiplication of a scalar to each element of a RegularVector2dField2d More... | |
| template<typename T , typename GridT > | |
| RegularVector2dField2d< T, GridT > | operator* (const T &val, const RegularVector2dField2d< T, GridT > &M1) |
| multiplication of a scalar to each element of a RegularVector2dField2d More... | |
| template<typename T , typename GridT > | |
| RegularVector2dField2d< T, GridT > | operator/ (const RegularVector2dField2d< T, GridT > &M1, const T &val) |
| division of a scalar to each element of a RegularVector2dField2d More... | |
| template<typename T , typename GridT > | |
| RegularVector2dField2d< T, GridT > | operator+ (const RegularVector2dField2d< T, GridT > &M1, const RegularVector2dField2d< T, GridT > &M2) |
| pointwise addition of two RegularVector2dField2d More... | |
| template<typename T , typename GridT > | |
| RegularVector2dField2d< T, GridT > | operator+ (const RegularVector2dField2d< T, GridT > &M1, const slip::Vector2d< T > &val) |
| addition of a Vector2d to each element of a RegularVector2dField2d More... | |
| template<typename T , typename GridT > | |
| RegularVector2dField2d< T, GridT > | operator+ (const slip::Vector2d< T > &val, const RegularVector2dField2d< T, GridT > &M1) |
| addition of a Vector2d to each element of a RegularVector2dField2d More... | |
| template<typename T , typename GridT > | |
| RegularVector2dField2d< T, GridT > | operator- (const RegularVector2dField2d< T, GridT > &M1, const RegularVector2dField2d< T, GridT > &M2) |
| pointwise substraction of two RegularVector2dField2d More... | |
| template<typename T , typename GridT > | |
| RegularVector2dField2d< T, GridT > | operator- (const RegularVector2dField2d< T, GridT > &M1, const slip::Vector2d< T > &val) |
| substraction of a Vector2d to each element of a RegularVector2dField2d More... | |
| template<typename T , typename GridT > | |
| RegularVector2dField2d< T, GridT > | operator- (const slip::Vector2d< T > &val, const RegularVector2dField2d< T, GridT > &M1) |
| substraction of a Vector2d to each element of a RegularVector2dField2d More... | |
| template<typename T , typename GridT > | |
| RegularVector2dField2d< T, GridT > | operator* (const RegularVector2dField2d< T, GridT > &M1, const RegularVector2dField2d< T, GridT > &M2) |
| pointwise multiplication of two RegularVector2dField2d More... | |
| template<typename T , typename GridT > | |
| RegularVector2dField2d< T, GridT > | operator* (const RegularVector2dField2d< T, GridT > &M1, const slip::Vector2d< T > &val) |
| multiplication of a Vector2d to each element of a RegularVector2dField2d More... | |
| template<typename T , typename GridT > | |
| RegularVector2dField2d< T, GridT > | operator* (const slip::Vector2d< T > &val, const RegularVector2dField2d< T, GridT > &M1) |
| multiplication of a Vector2d to each element of a RegularVector2dField2d More... | |
| template<typename T , typename GridT > | |
| RegularVector2dField2d< T, GridT > | operator/ (const RegularVector2dField2d< T, GridT > &M1, const RegularVector2dField2d< T, GridT > &M2) |
| pointwise division of two RegularVector2dField2d More... | |
| template<typename T , typename GridT > | |
| RegularVector2dField2d< T, GridT > | operator/ (const RegularVector2dField2d< T, GridT > &M1, const slip::Vector2d< T > &val) |
| division of a Vector2d to each element of a RegularVector2dField2d More... | |
| template<typename T , typename GridT > | |
| std::ostream & | operator<< (std::ostream &out, const slip::RegularVector3dField3d< T, GridT > &a) |
| template<typename T , typename GridT > | |
| RegularVector3dField3d< T, GridT > | operator+ (const RegularVector3dField3d< T, GridT > &M1, const T &val) |
| addition of a scalar to each element of a RegularVector3dField3d More... | |
| template<typename T , typename GridT > | |
| RegularVector3dField3d< T, GridT > | operator+ (const T &val, const RegularVector3dField3d< T, GridT > &M1) |
| addition of a scalar to each element of a RegularVector3dField3d More... | |
| template<typename T , typename GridT > | |
| RegularVector3dField3d< T, GridT > | operator- (const RegularVector3dField3d< T, GridT > &M1, const T &val) |
| substraction of a scalar to each element of a RegularVector3dField3d More... | |
| template<typename T , typename GridT > | |
| RegularVector3dField3d< T, GridT > | operator- (const T &val, const RegularVector3dField3d< T, GridT > &M1) |
| substraction of a scalar to each element of a RegularVector3dField3d More... | |
| template<typename T , typename GridT > | |
| RegularVector3dField3d< T, GridT > | operator* (const RegularVector3dField3d< T, GridT > &M1, const T &val) |
| multiplication of a scalar to each element of a RegularVector3dField3d More... | |
| template<typename T , typename GridT > | |
| RegularVector3dField3d< T, GridT > | operator* (const T &val, const RegularVector3dField3d< T, GridT > &M1) |
| multiplication of a scalar to each element of a RegularVector3dField3d More... | |
| template<typename T , typename GridT > | |
| RegularVector3dField3d< T, GridT > | operator/ (const RegularVector3dField3d< T, GridT > &M1, const T &val) |
| division of a scalar to each element of a RegularVector3dField3d More... | |
| template<typename T , typename GridT > | |
| RegularVector3dField3d< T, GridT > | operator+ (const RegularVector3dField3d< T, GridT > &M1, const RegularVector3dField3d< T, GridT > &M2) |
| pointwise addition of two RegularVector3dField3d More... | |
| template<typename T , typename GridT > | |
| RegularVector3dField3d< T, GridT > | operator+ (const RegularVector3dField3d< T, GridT > &M1, const slip::Vector3d< T > &val) |
| addition of a Vector3d to each element of a RegularVector3dField3d More... | |
| template<typename T , typename GridT > | |
| RegularVector3dField3d< T, GridT > | operator+ (const slip::Vector3d< T > &val, const RegularVector3dField3d< T, GridT > &M1) |
| addition of a Vector3d to each element of a RegularVector3dField3d More... | |
| template<typename T , typename GridT > | |
| RegularVector3dField3d< T, GridT > | operator- (const RegularVector3dField3d< T, GridT > &M1, const RegularVector3dField3d< T, GridT > &M2) |
| pointwise substraction of two RegularVector3dField3d More... | |
| template<typename T , typename GridT > | |
| RegularVector3dField3d< T, GridT > | operator- (const RegularVector3dField3d< T, GridT > &M1, const slip::Vector3d< T > &val) |
| substraction of a Vector3d to each element of a RegularVector3dField3d More... | |
| template<typename T , typename GridT > | |
| RegularVector3dField3d< T, GridT > | operator- (const slip::Vector3d< T > &val, const RegularVector3dField3d< T, GridT > &M1) |
| substraction of a Vector3d to each element of a RegularVector3dField3d More... | |
| template<typename T , typename GridT > | |
| RegularVector3dField3d< T, GridT > | operator* (const RegularVector3dField3d< T, GridT > &M1, const RegularVector3dField3d< T, GridT > &M2) |
| pointwise multiplication of two RegularVector3dField3d More... | |
| template<typename T , typename GridT > | |
| RegularVector3dField3d< T, GridT > | operator* (const RegularVector3dField3d< T, GridT > &M1, const slip::Vector3d< T > &val) |
| multiplication of a Vector3d to each element of a RegularVector3dField3d More... | |
| template<typename T , typename GridT > | |
| RegularVector3dField3d< T, GridT > | operator* (const slip::Vector3d< T > &val, const RegularVector3dField3d< T, GridT > &M1) |
| multiplication of a Vector3d to each element of a RegularVector3dField3d More... | |
| template<typename T , typename GridT > | |
| RegularVector3dField3d< T, GridT > | operator/ (const RegularVector3dField3d< T, GridT > &M1, const RegularVector3dField3d< T, GridT > &M2) |
| pointwise division of two RegularVector3dField3d More... | |
| template<typename T , typename GridT > | |
| RegularVector3dField3d< T, GridT > | operator/ (const RegularVector3dField3d< T, GridT > &M1, const slip::Vector3d< T > &val) |
| division of a Vector3d to each element of a RegularVector3dField3d More... | |
| template<typename T > | |
| std::ostream & | operator<< (std::ostream &out, const Signal< T > &v) |
| template<typename T > | |
| T & | min (const Signal< T > &V1) |
| template<typename T > | |
| T & | max (const Signal< T > &V1) |
| template<typename T > | |
| Signal< typename slip::lin_alg_traits< T > ::value_type > | abs (const Signal< T > &V) |
| template<typename T > | |
| Signal< T > | sqrt (const Signal< T > &V) |
| template<typename T > | |
| Signal< T > | cos (const Signal< T > &V) |
| Signal< float > | acos (const Signal< float > &V) |
| Signal< double > | acos (const Signal< double > &V) |
| Signal< long double > | acos (const Signal< long double > &V) |
| template<typename T > | |
| Signal< T > | sin (const Signal< T > &V) |
| Signal< float > | asin (const Signal< float > &V) |
| Signal< double > | asin (const Signal< double > &V) |
| Signal< long double > | asin (const Signal< long double > &V) |
| template<typename T > | |
| Signal< T > | tan (const Signal< T > &V) |
| Signal< float > | atan (const Signal< float > &V) |
| Signal< double > | atan (const Signal< double > &V) |
| Signal< long double > | atan (const Signal< long double > &V) |
| template<typename T > | |
| Signal< T > | exp (const Signal< T > &V) |
| template<typename T > | |
| Signal< T > | log (const Signal< T > &V) |
| template<typename T > | |
| Signal< T > | cosh (const Signal< T > &V) |
| template<typename T > | |
| Signal< T > | sinh (const Signal< T > &V) |
| template<typename T > | |
| Signal< T > | tanh (const Signal< T > &V) |
| template<typename T > | |
| Signal< T > | log10 (const Signal< T > &V) |
| template<typename Type > | |
| std::ostream & | operator<< (std::ostream &out, const slip::SoloffCamera< Type > &c) |
| template<typename T > | |
| std::ostream & | operator<< (std::ostream &out, const Vector< T > &v) |
| template<typename T > | |
| T & | min (const Vector< T > &V1) |
| template<typename T > | |
| T & | max (const Vector< T > &V1) |
| template<typename T > | |
| Vector< typename slip::lin_alg_traits< T > ::value_type > | abs (const Vector< T > &V) |
| template<typename T > | |
| Vector< T > | sqrt (const Vector< T > &V) |
| template<typename T > | |
| Vector< T > | cos (const Vector< T > &V) |
| Vector< float > | acos (const Vector< float > &V) |
| Vector< double > | acos (const Vector< double > &V) |
| Vector< long double > | acos (const Vector< long double > &V) |
| template<typename T > | |
| Vector< T > | sin (const Vector< T > &V) |
| Vector< float > | asin (const Vector< float > &V) |
| Vector< double > | asin (const Vector< double > &V) |
| Vector< long double > | asin (const Vector< long double > &V) |
| template<typename T > | |
| Vector< T > | tan (const Vector< T > &V) |
| Vector< float > | atan (const Vector< float > &V) |
| Vector< double > | atan (const Vector< double > &V) |
| Vector< long double > | atan (const Vector< long double > &V) |
| template<typename T > | |
| Vector< T > | exp (const Vector< T > &V) |
| template<typename T > | |
| Vector< T > | log (const Vector< T > &V) |
| template<typename T > | |
| Vector< T > | cosh (const Vector< T > &V) |
| template<typename T > | |
| Vector< T > | sinh (const Vector< T > &V) |
| template<typename T > | |
| Vector< T > | tanh (const Vector< T > &V) |
| template<typename T > | |
| Vector< T > | log10 (const Vector< T > &V) |
| template<typename T > | |
| Vector2d< T > | operator+ (const Vector2d< T > &V1, const Vector2d< T > &V2) |
| template<typename T > | |
| Vector2d< T > | operator+ (const Vector2d< T > &V1, const T &val) |
| template<typename T > | |
| Vector2d< T > | operator+ (const T &val, const Vector2d< T > &V1) |
| template<typename T > | |
| Vector2d< T > | operator- (const Vector2d< T > &V1, const Vector2d< T > &V2) |
| template<typename T > | |
| Vector2d< T > | operator- (const Vector2d< T > &V1, const T &val) |
| template<typename T > | |
| Vector2d< T > | operator- (const T &val, const Vector2d< T > &V1) |
| template<typename T > | |
| Vector2d< T > | operator* (const Vector2d< T > &V1, const Vector2d< T > &V2) |
| template<typename T > | |
| Vector2d< T > | operator* (const Vector2d< T > &V1, const T &val) |
| template<typename T > | |
| Vector2d< T > | operator* (const T &val, const Vector2d< T > &V1) |
| template<typename T > | |
| Vector2d< T > | operator/ (const Vector2d< T > &V1, const Vector2d< T > &V2) |
| template<typename T > | |
| Vector2d< T > | operator/ (const Vector2d< T > &V1, const T &val) |
| template<typename T > | |
| Vector3d< T > | operator+ (const Vector3d< T > &V1, const Vector3d< T > &V2) |
| template<typename T > | |
| Vector3d< T > | operator+ (const Vector3d< T > &V1, const T &val) |
| template<typename T > | |
| Vector3d< T > | operator+ (const T &val, const Vector3d< T > &V1) |
| template<typename T > | |
| Vector3d< T > | operator- (const Vector3d< T > &V1, const Vector3d< T > &V2) |
| template<typename T > | |
| Vector3d< T > | operator- (const Vector3d< T > &V1, const T &val) |
| template<typename T > | |
| Vector3d< T > | operator- (const T &val, const Vector3d< T > &V1) |
| template<typename T > | |
| Vector3d< T > | operator* (const Vector3d< T > &V1, const Vector3d< T > &V2) |
| template<typename T > | |
| Vector3d< T > | operator* (const Vector3d< T > &V1, const T &val) |
| template<typename T > | |
| Vector3d< T > | operator* (const T &val, const Vector3d< T > &V1) |
| template<typename T > | |
| Vector3d< T > | operator/ (const Vector3d< T > &V1, const Vector3d< T > &V2) |
| template<typename T > | |
| Vector3d< T > | operator/ (const Vector3d< T > &V1, const T &val) |
| template<typename T > | |
| Vector4d< T > | operator+ (const Vector4d< T > &V1, const Vector4d< T > &V2) |
| template<typename T > | |
| Vector4d< T > | operator+ (const Vector4d< T > &V1, const T &val) |
| template<typename T > | |
| Vector4d< T > | operator+ (const T &val, const Vector4d< T > &V1) |
| template<typename T > | |
| Vector4d< T > | operator- (const Vector4d< T > &V1, const Vector4d< T > &V2) |
| template<typename T > | |
| Vector4d< T > | operator- (const Vector4d< T > &V1, const T &val) |
| template<typename T > | |
| Vector4d< T > | operator- (const T &val, const Vector4d< T > &V1) |
| template<typename T > | |
| Vector4d< T > | operator* (const Vector4d< T > &V1, const Vector4d< T > &V2) |
| template<typename T > | |
| Vector4d< T > | operator* (const Vector4d< T > &V1, const T &val) |
| template<typename T > | |
| Vector4d< T > | operator* (const T &val, const Vector4d< T > &V1) |
| template<typename T > | |
| Vector4d< T > | operator/ (const Vector4d< T > &V1, const Vector4d< T > &V2) |
| template<typename T > | |
| Vector4d< T > | operator/ (const Vector4d< T > &V1, const T &val) |
| template<typename T > | |
| Volume< T > | operator+ (const Volume< T > &M1, const Volume< T > &M2) |
| pointwise addition of two Volume More... | |
| template<typename T > | |
| Volume< T > | operator+ (const Volume< T > &M1, const T &val) |
| addition of a scalar to each element of a Volume More... | |
| template<typename T > | |
| Volume< T > | operator+ (const T &val, const Volume< T > &M1) |
| addition of a scalar to each element of a Volume More... | |
| template<typename T > | |
| Volume< T > | operator- (const Volume< T > &M1, const Volume< T > &M2) |
| pointwise substraction of two Volume More... | |
| template<typename T > | |
| Volume< T > | operator- (const Volume< T > &M1, const T &val) |
| substraction of a scalar to each element of a Volume More... | |
| template<typename T > | |
| Volume< T > | operator- (const T &val, const Volume< T > &M1) |
| substraction of a scalar to each element of a Volume More... | |
| template<typename T > | |
| Volume< T > | operator* (const Volume< T > &M1, const Volume< T > &M2) |
| pointwise multiplication of two Volume More... | |
| template<typename T > | |
| Volume< T > | operator* (const Volume< T > &M1, const T &val) |
| multiplication of a scalar to each element of a Volume More... | |
| template<typename T > | |
| Volume< T > | operator* (const T &val, const Volume< T > &M1) |
| multiplication of a scalar to each element of a Volume More... | |
| template<typename T > | |
| Volume< T > | operator/ (const Volume< T > &M1, const Volume< T > &M2) |
| pointwise division of two Volume More... | |
| template<typename T > | |
| Volume< T > | operator/ (const Volume< T > &M1, const T &val) |
| division of a scalar to each element of a Volume More... | |
| template<typename T > | |
| T & | min (const Volume< T > &M1) |
| template<typename T > | |
| T & | max (const Volume< T > &M1) |
| template<typename T > | |
| Volume< T > | abs (const Volume< T > &M) |
| template<typename T > | |
| Volume< T > | sqrt (const Volume< T > &M) |
| template<typename T > | |
| Volume< T > | cos (const Volume< T > &M) |
| template<typename T > | |
| Volume< T > | acos (const Volume< T > &M) |
| template<typename T > | |
| Volume< T > | sin (const Volume< T > &M) |
| template<typename T > | |
| Volume< T > | asin (const Volume< T > &M) |
| template<typename T > | |
| Volume< T > | tan (const Volume< T > &M) |
| template<typename T > | |
| Volume< T > | atan (const Volume< T > &M) |
| template<typename T > | |
| Volume< T > | exp (const Volume< T > &M) |
| template<typename T > | |
| Volume< T > | log (const Volume< T > &M) |
| template<typename T > | |
| Volume< T > | cosh (const Volume< T > &M) |
| template<typename T > | |
| Volume< T > | sinh (const Volume< T > &M) |
| template<typename T > | |
| Volume< T > | tanh (const Volume< T > &M) |
| template<typename T > | |
| Volume< T > | log10 (const Volume< T > &M) |
Applies an unary C-function with non const parameter | |
| template<typename InputIterator , typename OutputIterator > | |
| void | apply (InputIterator first, InputIterator last, OutputIterator result, typename std::iterator_traits< OutputIterator >::value_type(*function)(typename std::iterator_traits< InputIterator >::value_type)) |
| Applies a C-function to each element of a range. More... | |
| template<typename InputIterator , typename OutputIterator , typename MaskIterator > | |
| void | apply_mask (InputIterator first, InputIterator last, MaskIterator mask_first, OutputIterator result, typename std::iterator_traits< OutputIterator >::value_type(*function)(typename std::iterator_traits< InputIterator >::value_type), typename std::iterator_traits< MaskIterator >::value_type value=typename std::iterator_traits< MaskIterator >::value_type(1)) |
| Applies a C-function to each element of a range according to a mask range. More... | |
| template<typename InputIterator , typename OutputIterator , typename Predicate > | |
| void | apply_if (InputIterator first, InputIterator last, OutputIterator result, Predicate pred, typename std::iterator_traits< OutputIterator >::value_type(*function)(typename std::iterator_traits< InputIterator >::value_type)) |
| Applies a C-function to each element of a range according to a predicate. More... | |
Apply an unary C-function with a const parameter | |
| template<typename InputIterator , typename OutputIterator > | |
| void | apply (InputIterator first, InputIterator last, OutputIterator result, typename std::iterator_traits< OutputIterator >::value_type(*function)(const typename std::iterator_traits< InputIterator >::value_type &)) |
| Applies a C-function to each element of a range. More... | |
| template<typename InputIterator , typename OutputIterator , typename MaskIterator > | |
| void | apply_mask (InputIterator first, InputIterator last, MaskIterator mask_first, OutputIterator result, typename std::iterator_traits< OutputIterator >::value_type(*function)(const typename std::iterator_traits< InputIterator >::value_type &), typename std::iterator_traits< MaskIterator >::value_type value=typename std::iterator_traits< MaskIterator >::value_type(1)) |
| Applies a C-function to each element of a range according to a mask range. More... | |
| template<typename InputIterator , typename OutputIterator , typename Predicate > | |
| void | apply_if (InputIterator first, InputIterator last, OutputIterator result, Predicate pred, typename std::iterator_traits< OutputIterator >::value_type(*function)(const typename std::iterator_traits< InputIterator >::value_type &)) |
| Applies a C-function to each element of a range according to a predicate. More... | |
Applies a binary C-function with two non const parameters | |
| template<typename InputIterator1 , typename InputIterator2 , typename OutputIterator > | |
| void | apply (InputIterator1 first, InputIterator1 last, InputIterator2 first2, OutputIterator result, typename std::iterator_traits< OutputIterator >::value_type(*function)(typename std::iterator_traits< InputIterator1 >::value_type, typename std::iterator_traits< InputIterator2 >::value_type)) |
| Applies a two-parameter C-function to each element of two ranges. More... | |
| template<typename InputIterator1 , typename InputIterator2 , typename OutputIterator , typename MaskIterator > | |
| void | apply_mask (InputIterator1 first, InputIterator1 last, MaskIterator mask_first, InputIterator2 first2, OutputIterator result, typename std::iterator_traits< OutputIterator >::value_type(*function)(typename std::iterator_traits< InputIterator1 >::value_type, typename std::iterator_traits< InputIterator2 >::value_type), typename std::iterator_traits< MaskIterator >::value_type value=typename std::iterator_traits< MaskIterator >::value_type(1)) |
| Applies a C-function to each element of a range according to a mask range. More... | |
| template<typename InputIterator1 , typename InputIterator2 , typename OutputIterator , typename Predicate > | |
| void | apply_if (InputIterator1 first, InputIterator1 last, InputIterator2 first2, OutputIterator result, Predicate pred, typename std::iterator_traits< OutputIterator >::value_type(*function)(typename std::iterator_traits< InputIterator1 >::value_type, typename std::iterator_traits< InputIterator2 >::value_type)) |
| Applies a C-function to each element of a range according to a predicate. More... | |
Applies a binary C-function with two const parameters | |
| template<typename InputIterator1 , typename InputIterator2 , typename OutputIterator > | |
| void | apply (InputIterator1 first, InputIterator1 last, InputIterator2 first2, OutputIterator result, typename std::iterator_traits< OutputIterator >::value_type(*function)(const typename std::iterator_traits< InputIterator1 >::value_type &, const typename std::iterator_traits< InputIterator2 >::value_type &)) |
| Applies a two-const-parameter C-function to each element of two ranges. More... | |
| template<typename InputIterator1 , typename InputIterator2 , typename OutputIterator , typename MaskIterator > | |
| void | apply_mask (InputIterator1 first, InputIterator1 last, MaskIterator mask_first, InputIterator2 first2, OutputIterator result, typename std::iterator_traits< OutputIterator >::value_type(*function)(const typename std::iterator_traits< InputIterator1 >::value_type &, const typename std::iterator_traits< InputIterator2 >::value_type &), typename std::iterator_traits< MaskIterator >::value_type value=typename std::iterator_traits< MaskIterator >::value_type(1)) |
| Applies a C-function to each element of a range according to a mask range. More... | |
| template<typename InputIterator1 , typename InputIterator2 , typename OutputIterator , typename Predicate > | |
| void | apply_if (InputIterator1 first, InputIterator1 last, InputIterator2 first2, OutputIterator result, Predicate pred, typename std::iterator_traits< OutputIterator >::value_type(*function)(const typename std::iterator_traits< InputIterator1 >::value_type &, const typename std::iterator_traits< InputIterator2 >::value_type &)) |
| Applies a C-function to each element of a range according to a predicate. More... | |
Operations between two ranges | |
| template<typename InputIterator1 , typename InputIterator2 , typename OutputIterator > | |
| void | plus (InputIterator1 __first1, InputIterator1 __last1, InputIterator2 __first2, OutputIterator __result) |
| Computes the addition of two ranges. More... | |
| template<typename _InputIterator1 , typename _InputIterator2 , typename _MaskIterator , typename _OutputIterator > | |
| void | plus_mask (_InputIterator1 __first1, _InputIterator1 __last1, _MaskIterator __mask_first, _InputIterator2 __first2, _OutputIterator __result, typename std::iterator_traits< _MaskIterator >::value_type value=typename std::iterator_traits< _MaskIterator >::value_type(1)) |
| Computes the addition of two ranges according to a mask sequence. More... | |
| template<typename _InputIterator1 , typename _InputIterator2 , typename _OutputIterator , typename _Predicate > | |
| void | plus_if (_InputIterator1 __first1, _InputIterator1 __last1, _InputIterator2 __first2, _OutputIterator __result, _Predicate __pred) |
| Computes the addition of two ranges according to a Predicate. More... | |
| template<typename InputIterator1 , typename InputIterator2 , typename OutputIterator > | |
| void | minus (InputIterator1 __first1, InputIterator1 __last1, InputIterator2 __first2, OutputIterator __result) |
| Computes the difference of two ranges. More... | |
| template<typename _InputIterator1 , typename _InputIterator2 , typename _MaskIterator , typename _OutputIterator > | |
| void | minus_mask (_InputIterator1 __first1, _InputIterator1 __last1, _MaskIterator __mask_first, _InputIterator2 __first2, _OutputIterator __result, typename std::iterator_traits< _MaskIterator >::value_type value=typename std::iterator_traits< _MaskIterator >::value_type(1)) |
| Computes the difference of two ranges according to a mask sequence. More... | |
| template<typename _InputIterator1 , typename _InputIterator2 , typename _OutputIterator , typename _Predicate > | |
| void | minus_if (_InputIterator1 __first1, _InputIterator1 __last1, _InputIterator2 __first2, _OutputIterator __result, _Predicate __pred) |
| Computes the difference of two ranges according to a Predicate. More... | |
| template<typename InputIterator1 , typename InputIterator2 , typename OutputIterator > | |
| void | multiplies (InputIterator1 __first1, InputIterator1 __last1, InputIterator2 __first2, OutputIterator __result) |
| Computes the pointwise product of two ranges. More... | |
| template<typename _InputIterator1 , typename _InputIterator2 , typename _MaskIterator , typename _OutputIterator > | |
| void | multiplies_mask (_InputIterator1 __first1, _InputIterator1 __last1, _MaskIterator __mask_first, _InputIterator2 __first2, _OutputIterator __result, typename std::iterator_traits< _MaskIterator >::value_type value=typename std::iterator_traits< _MaskIterator >::value_type(1)) |
| Computes the pointwise product of two ranges according to a mask sequence. More... | |
| template<typename _InputIterator1 , typename _InputIterator2 , typename _OutputIterator , typename _Predicate > | |
| void | multiplies_if (_InputIterator1 __first1, _InputIterator1 __last1, _InputIterator2 __first2, _OutputIterator __result, _Predicate __pred) |
| Computes the pointwise product of two ranges according to a Predicate. More... | |
| template<typename InputIterator1 , typename InputIterator2 , typename OutputIterator > | |
| void | divides (InputIterator1 __first1, InputIterator1 __last1, InputIterator2 __first2, OutputIterator __result) |
| Computes the pointwise division of two ranges. More... | |
| template<typename _InputIterator1 , typename _InputIterator2 , typename _MaskIterator , typename _OutputIterator > | |
| void | divides_mask (_InputIterator1 __first1, _InputIterator1 __last1, _MaskIterator __mask_first, _InputIterator2 __first2, _OutputIterator __result, typename std::iterator_traits< _MaskIterator >::value_type value=typename std::iterator_traits< _MaskIterator >::value_type(1)) |
| Computes the pointwise division of two ranges according to a mask sequence. More... | |
| template<typename _InputIterator1 , typename _InputIterator2 , typename _OutputIterator , typename _Predicate > | |
| void | divides_if (_InputIterator1 __first1, _InputIterator1 __last1, _InputIterator2 __first2, _OutputIterator __result, _Predicate __pred) |
| Computes the pointwise division of two ranges. according to a Predicate. More... | |
| template<typename InputIterator1 , typename InputIterator2 , typename OutputIterator > | |
| void | minimum (InputIterator1 __first1, InputIterator1 __last1, InputIterator2 __first2, OutputIterator __result) |
| Computes the minimum of two ranges. More... | |
| template<typename _InputIterator1 , typename _InputIterator2 , typename _MaskIterator , typename _OutputIterator > | |
| void | minimum_mask (_InputIterator1 __first1, _InputIterator1 __last1, _MaskIterator __mask_first, _InputIterator2 __first2, _OutputIterator __result, typename std::iterator_traits< _MaskIterator >::value_type value=typename std::iterator_traits< _MaskIterator >::value_type(1)) |
| Computes the minimum of two ranges according to a mask sequence. More... | |
| template<typename _InputIterator1 , typename _InputIterator2 , typename _OutputIterator , typename _Predicate > | |
| void | minimum_if (_InputIterator1 __first1, _InputIterator1 __last1, _InputIterator2 __first2, _OutputIterator __result, _Predicate __pred) |
| Computes the minimum of two ranges according to a Predicate. More... | |
| template<typename InputIterator1 , typename InputIterator2 , typename OutputIterator > | |
| void | maximum (InputIterator1 __first1, InputIterator1 __last1, InputIterator2 __first2, OutputIterator __result) |
| Computes the maximum of two ranges. More... | |
| template<typename _InputIterator1 , typename _InputIterator2 , typename _MaskIterator , typename _OutputIterator > | |
| void | maximum_mask (_InputIterator1 __first1, _InputIterator1 __last1, _MaskIterator __mask_first, _InputIterator2 __first2, _OutputIterator __result, typename std::iterator_traits< _MaskIterator >::value_type value=typename std::iterator_traits< _MaskIterator >::value_type(1)) |
| Computes the maximum of two ranges according to a mask sequence. More... | |
| template<typename _InputIterator1 , typename _InputIterator2 , typename _OutputIterator , typename _Predicate > | |
| void | maximum_if (_InputIterator1 __first1, _InputIterator1 __last1, _InputIterator2 __first2, _OutputIterator __result, _Predicate __pred) |
| Computes the maximum of two ranges according to a Predicate. More... | |
Operations between a range and a scalar | |
| template<typename InputIterator1 , typename OutputIterator > | |
| void | plus_scalar (InputIterator1 __first1, InputIterator1 __last1, const typename std::iterator_traits< InputIterator1 >::value_type &scalar, OutputIterator __result) |
| Adds a scalar to a range. More... | |
| template<typename _InputIterator1 , typename _MaskIterator , typename _OutputIterator > | |
| void | plus_scalar_mask (_InputIterator1 __first1, _InputIterator1 __last1, _MaskIterator __mask_first, const typename std::iterator_traits< _InputIterator1 >::value_type &scalar, _OutputIterator __result, typename std::iterator_traits< _MaskIterator >::value_type value=typename std::iterator_traits< _MaskIterator >::value_type(1)) |
| Adds a scalar to a range according to a mask sequence. More... | |
| template<typename _InputIterator1 , typename _OutputIterator , typename _Predicate > | |
| void | plus_scalar_if (_InputIterator1 __first1, _InputIterator1 __last1, const typename std::iterator_traits< _InputIterator1 >::value_type &scalar, _OutputIterator __result, _Predicate __pred) |
| Adds a scalar to a range according to a Predicate. More... | |
| template<typename InputIterator1 , typename OutputIterator > | |
| void | minus_scalar (InputIterator1 __first1, InputIterator1 __last1, const typename std::iterator_traits< InputIterator1 >::value_type &scalar, OutputIterator __result) |
| Substracts a scalar to a range. More... | |
| template<typename _InputIterator1 , typename _MaskIterator , typename _OutputIterator > | |
| void | minus_scalar_mask (_InputIterator1 __first1, _InputIterator1 __last1, _MaskIterator __mask_first, const typename std::iterator_traits< _InputIterator1 >::value_type &scalar, _OutputIterator __result, typename std::iterator_traits< _MaskIterator >::value_type value=typename std::iterator_traits< _MaskIterator >::value_type(1)) |
| Substracts a scalar to a range according to a mask sequence. More... | |
| template<typename _InputIterator1 , typename _OutputIterator , typename _Predicate > | |
| void | minus_scalar_if (_InputIterator1 __first1, _InputIterator1 __last1, const typename std::iterator_traits< _InputIterator1 >::value_type &scalar, _OutputIterator __result, _Predicate __pred) |
| Substracts a scalar to a range according to a Predicate. More... | |
| template<typename InputIterator1 , typename OutputIterator > | |
| void | multiplies_scalar (InputIterator1 __first1, InputIterator1 __last1, const typename std::iterator_traits< InputIterator1 >::value_type &scalar, OutputIterator __result) |
| Multiplies a range by a scalar. More... | |
| template<typename _InputIterator1 , typename _MaskIterator , typename _OutputIterator > | |
| void | multiplies_scalar_mask (_InputIterator1 __first1, _InputIterator1 __last1, _MaskIterator __mask_first, const typename std::iterator_traits< _InputIterator1 >::value_type &scalar, _OutputIterator __result, typename std::iterator_traits< _MaskIterator >::value_type value=typename std::iterator_traits< _MaskIterator >::value_type(1)) |
| Multiplies a range by a scalar according to a mask sequence. More... | |
| template<typename _InputIterator1 , typename _OutputIterator , typename _Predicate > | |
| void | multiplies_scalar_if (_InputIterator1 __first1, _InputIterator1 __last1, const typename std::iterator_traits< _InputIterator1 >::value_type &scalar, _OutputIterator __result, _Predicate __pred) |
| Multiplies a range by a scalar according to a Predicate. More... | |
| template<typename InputIterator1 , typename OutputIterator > | |
| void | divides_scalar (InputIterator1 __first1, InputIterator1 __last1, const typename std::iterator_traits< InputIterator1 >::value_type &scalar, OutputIterator __result) |
| Divides a range by a scalar. More... | |
| template<typename _InputIterator1 , typename _MaskIterator , typename _OutputIterator > | |
| void | divides_scalar_mask (_InputIterator1 __first1, _InputIterator1 __last1, _MaskIterator __mask_first, const typename std::iterator_traits< _InputIterator1 >::value_type &scalar, _OutputIterator __result, typename std::iterator_traits< _MaskIterator >::value_type value=typename std::iterator_traits< _MaskIterator >::value_type(1)) |
| Divides a range by a scalar according to a mask sequence. More... | |
| template<typename _InputIterator1 , typename _OutputIterator , typename _Predicate > | |
| void | divides_scalar_if (_InputIterator1 __first1, _InputIterator1 __last1, const typename std::iterator_traits< _InputIterator1 >::value_type &scalar, _OutputIterator __result, _Predicate __pred) |
| Divides a range by a scalar according to a Predicate. More... | |
Operations on a range | |
| template<typename InputIterator , typename OutputIterator > | |
| void | negate (InputIterator __first1, InputIterator __last1, OutputIterator __result) |
| Computes the negation of a range. More... | |
| template<typename InputIterator , typename MaskIterator , typename OutputIterator > | |
| void | negate_mask (InputIterator __first1, InputIterator __last1, MaskIterator __mask_first, OutputIterator __result, typename std::iterator_traits< MaskIterator >::value_type value=typename std::iterator_traits< MaskIterator >::value_type(1)) |
| Computes the negation of a range according to a mask range. More... | |
| template<typename _InputIterator1 , typename _OutputIterator , typename _Predicate > | |
| void | negate_if (_InputIterator1 __first1, _InputIterator1 __last1, _OutputIterator __result, _Predicate __pred) |
| Computes the pointwise negate of a ranges according to a Predicate. More... | |
| template<class ForwardIterator , class T > | |
| void | iota (ForwardIterator first, ForwardIterator last, T value, T step=T(1)) |
| Iota assigns sequential increasing values based on a predefined step to a range. That is, it assigns value to *first, value + step to *(first + 1) and so on. In general, each iterator i in the range [first,last) is assigned value + step * (i - first). More... | |
| template<class ForwardIterator , typename MaskIterator , class T > | |
| void | iota_mask (ForwardIterator first, ForwardIterator last, MaskIterator mask_first, T value, T step=T(1), typename std::iterator_traits< MaskIterator >::value_type value_mask=typename std::iterator_traits< MaskIterator >::value_type(1)) |
| Iota_mask sequential increasing values based on a predefined step to a range according to a mask sequence. More... | |
Generic distance algorithms | |
| template<typename Real , typename InputIterator1 , typename InputIterator2 , typename BinaryFunctor > | |
| Real | distance (InputIterator1 first1, InputIterator1 last1, InputIterator2 first2, BinaryFunctor distance) |
Computes the sum of the pointwise distances of two ranges: 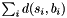 according to the distance d. More... according to the distance d. More... | |
| template<typename Real , typename InputIterator1 , typename InputIterator2 , typename BinaryFunctor , typename MaskIterator > | |
| Real | distance_mask (InputIterator1 first1, InputIterator1 last1, MaskIterator mask_first, InputIterator2 first2, BinaryFunctor distance, typename std::iterator_traits< MaskIterator >::value_type value=typename std::iterator_traits< MaskIterator >::value_type(1)) |
Computes the sum of the pointwise distances of two ranges: 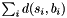 according to the distance d and the given mask range. More... according to the distance d and the given mask range. More... | |
| template<typename Real , typename InputIterator1 , typename InputIterator2 , typename BinaryFunctor , typename Predicate > | |
| Real | distance_if (InputIterator1 first1, InputIterator1 last1, InputIterator2 first2, BinaryFunctor distance, Predicate pred) |
Computes the sum of the pointwise distances of two ranges: 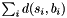 according to the distance d and the given predicate. More... according to the distance d and the given predicate. More... | |
Generic distance map algorithms | |
| template<typename InputIterator1 , typename InputIterator2 , typename OutputIterator , typename BinaryFunctor > | |
| void | distance (InputIterator1 first1, InputIterator1 last1, InputIterator2 first2, OutputIterator result, BinaryFunctor distance) |
Computes the pointwise distances of two ranges: 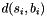 . More... . More... | |
| template<typename InputIterator1 , typename InputIterator2 , typename MaskIterator , typename OutputIterator , typename BinaryFunctor > | |
| void | distance_mask (InputIterator1 first1, InputIterator1 last1, MaskIterator mask_first, InputIterator2 first2, OutputIterator result, BinaryFunctor distance, typename std::iterator_traits< MaskIterator >::value_type value=typename std::iterator_traits< MaskIterator >::value_type(1)) |
Computes the pointwise distances of two ranges: 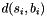 according to a given mask range. More... according to a given mask range. More... | |
| template<typename _InputIterator1 , typename _InputIterator2 , typename _OutputIterator , typename _BinaryOperation , typename _Predicate > | |
| void | distance_if (_InputIterator1 first1, _InputIterator1 last1, _InputIterator2 first2, _OutputIterator result, _BinaryOperation distance, _Predicate pred) |
Computes the pointwise distances of two ranges: 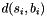 according to a Predicate. More... according to a Predicate. More... | |
Specific distance algorithms | |
| template<typename Value_T , typename InputIterator1 , typename InputIterator2 > | |
| Value_T | mean_square_diff (InputIterator1 first1, InputIterator1 last1, InputIterator2 first2) |
Computes the mean square of the pointwise difference of two ranges of size N: 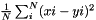 . More... . More... | |
| template<typename Real , typename InputIterator1 , typename InputIterator2 , typename MaskIterator > | |
| Real | mean_square_diff_mask (InputIterator1 first1, InputIterator1 last1, MaskIterator mask_first, InputIterator2 first2, typename std::iterator_traits< MaskIterator >::value_type value=typename std::iterator_traits< MaskIterator >::value_type(1)) |
Computes the mean square of the pointwise difference of two ranges of size N according to a mask sequence : 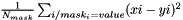 . More... . More... | |
| template<typename Real , typename InputIterator1 , typename InputIterator2 , typename Predicate > | |
| Real | mean_square_diff_if (InputIterator1 first1, InputIterator1 last1, InputIterator2 first2, Predicate pred) |
Computes the mean square of the pointwise difference of two ranges according to a Predicate : 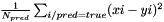 . More... . More... | |
| template<typename Value_T , typename InputIterator1 , typename InputIterator2 > | |
| Value_T | mean_abs_diff (InputIterator1 first1, InputIterator1 last1, InputIterator2 first2) |
Computes the mean absolute difference of two range of size N: 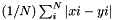 . More... . More... | |
| template<typename Value_T , typename InputIterator1 , typename InputIterator2 , typename MaskIterator > | |
| Value_T | mean_abs_diff_mask (InputIterator1 first1, InputIterator1 last1, MaskIterator mask_first, InputIterator2 first2, typename std::iterator_traits< MaskIterator >::value_type value=typename std::iterator_traits< MaskIterator >::value_type(1)) |
Computes the mean absolute difference of two ranges of size N according to a mask sequence : 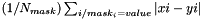 . More... . More... | |
| template<typename Real , typename InputIterator1 , typename InputIterator2 , typename Predicate > | |
| Real | mean_abs_diff_if (InputIterator1 first1, InputIterator1 last1, InputIterator2 first2, Predicate pred) |
| Computes the mean absolute difference of two ranges according to a Predicate. More... | |
| template<typename Real , typename InputIterator1 , typename InputIterator2 > | |
| Real | snr (InputIterator1 first1, InputIterator1 last1, InputIterator2 first2) |
Computes the signal to noise ration (snr) of two ranges : 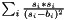 . More... . More... | |
| template<typename Real , typename InputIterator1 , typename InputIterator2 , typename MaskIterator > | |
| Real | snr_mask (InputIterator1 first1, InputIterator1 last1, MaskIterator mask_first, InputIterator2 first2, typename std::iterator_traits< MaskIterator >::value_type value=typename std::iterator_traits< MaskIterator >::value_type(1)) |
Computes the signal to noise ration (snr) of two ranges according to a mask sequence : 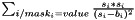 . More... . More... | |
| template<typename Real , typename InputIterator1 , typename InputIterator2 , typename Predicate > | |
| Real | snr_if (InputIterator1 first1, InputIterator1 last1, InputIterator2 first2, Predicate pred) |
| Computes the signal to noise ration (snr) of two ranges according to a Predicate. More... | |
| template<typename Real , typename InputIterator1 , typename InputIterator2 > | |
| Real | snr_dB (InputIterator1 first1, InputIterator1 last1, InputIterator2 first2) |
Computes the decibel signal to noise ration (snr) of two ranges : 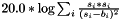 . More... . More... | |
| template<typename Real , typename InputIterator1 , typename InputIterator2 , typename MaskIterator > | |
| Real | snr_dB_mask (InputIterator1 first1, InputIterator1 last1, MaskIterator mask_first, InputIterator2 first2, typename std::iterator_traits< MaskIterator >::value_type value=typename std::iterator_traits< MaskIterator >::value_type(1)) |
Computes the decibel signal to noise ration (snr) of two ranges according to a mask sequence : 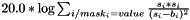 . More... . More... | |
| template<typename Real , typename InputIterator1 , typename InputIterator2 , typename Predicate > | |
| Real | snr_dB_if (InputIterator1 first1, InputIterator1 last1, InputIterator2 first2, Predicate pred) |
Computes the decibel signal to noise ration (snr) of two ranges according to a predicate: 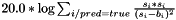 . More... . More... | |
| template<typename Real , typename InputIterator1 , typename InputIterator2 > | |
| Real | L22_distance (InputIterator1 first1, InputIterator1 last1, InputIterator2 first2) |
Computes the square euclidian distance of two ranges: 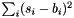 . More... . More... | |
| template<typename Real , typename InputIterator1 , typename InputIterator2 , typename MaskIterator > | |
| Real | L22_distance_mask (InputIterator1 first1, InputIterator1 last1, MaskIterator mask_first, InputIterator2 first2, typename std::iterator_traits< MaskIterator >::value_type value=typename std::iterator_traits< MaskIterator >::value_type(1)) |
Computes the square eucludian distance of two ranges according to a mask sequence : 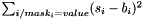 . More... . More... | |
| template<typename Real , typename InputIterator1 , typename InputIterator2 , typename Predicate > | |
| Real | L22_distance_if (InputIterator1 first1, InputIterator1 last1, InputIterator2 first2, Predicate pred) |
| Computes the square eucludian distance of two ranges according to a Predicate. More... | |
| template<typename Real , typename InputIterator1 , typename InputIterator2 > | |
| Real | L2_distance (InputIterator1 first1, InputIterator1 last1, InputIterator2 first2) |
Computes the Euclidian distance of two ranges : 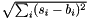 . More... . More... | |
| template<typename Real , typename InputIterator1 , typename InputIterator2 , typename MaskIterator > | |
| Real | L2_distance_mask (InputIterator1 first1, InputIterator1 last1, MaskIterator mask_first, InputIterator2 first2, typename std::iterator_traits< MaskIterator >::value_type value=typename std::iterator_traits< MaskIterator >::value_type(1)) |
Computes the eucludian distance of two ranges according to a mask sequence : 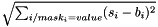 . More... . More... | |
| template<typename Real , typename InputIterator1 , typename InputIterator2 , typename Predicate > | |
| Real | L2_distance_if (InputIterator1 first1, InputIterator1 last1, InputIterator2 first2, Predicate pred) |
| Computes the eucludian distance of two ranges according to a Predicate. More... | |
| template<typename Real , typename InputIterator1 , typename InputIterator2 > | |
| Real | L1_distance (InputIterator1 first1, InputIterator1 last1, InputIterator2 first2) |
Computes the L1 distance of two ranges : 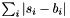 . More... . More... | |
| template<typename Real , typename InputIterator1 , typename InputIterator2 , typename MaskIterator > | |
| Real | L1_distance_mask (InputIterator1 first1, InputIterator1 last1, MaskIterator mask_first, InputIterator2 first2, typename std::iterator_traits< MaskIterator >::value_type value=typename std::iterator_traits< MaskIterator >::value_type(1)) |
Computes the L1 distance of two ranges according to a mask sequence : 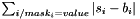 . More... . More... | |
| template<typename Real , typename InputIterator1 , typename InputIterator2 , typename Predicate > | |
| Real | L1_distance_if (InputIterator1 first1, InputIterator1 last1, InputIterator2 first2, Predicate pred) |
| Computes the L1 distance of two ranges according to a Predicate. More... | |
| template<typename Real , typename InputIterator1 , typename InputIterator2 > | |
| Real | Minkowski_distance (const std::size_t n, InputIterator1 first1, InputIterator1 last1, InputIterator2 first2) |
Computes the Minkowski order n distance of two ranges : 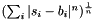 Use L1 and L2 distance for n=1 or 2. More... Use L1 and L2 distance for n=1 or 2. More... | |
| template<typename Real , typename InputIterator1 , typename InputIterator2 , typename MaskIterator > | |
| Real | Minkowski_distance_mask (const std::size_t n, InputIterator1 first1, InputIterator1 last1, MaskIterator mask_first, InputIterator2 first2, typename std::iterator_traits< MaskIterator >::value_type value=typename std::iterator_traits< MaskIterator >::value_type(1)) |
Computes the Minkowski order n distance of two ranges according to a mask sequence : 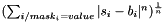 . More... . More... | |
| template<typename Real , typename InputIterator1 , typename InputIterator2 , typename Predicate > | |
| Real | Minkowski_distance_if (const std::size_t n, InputIterator1 first1, InputIterator1 last1, InputIterator2 first2, Predicate pred) |
| Computes the Minkowski order n distance of two ranges according to a Predicate. More... | |
| template<typename Real , typename InputIterator1 , typename InputIterator2 > | |
| Real | Linf_distance (InputIterator1 first1, InputIterator1 last1, InputIterator2 first2) |
Computes the Linfinite distance of two ranges : 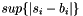 . More... . More... | |
| template<typename Real , typename InputIterator1 , typename InputIterator2 , typename MaskIterator > | |
| Real | Linf_distance_mask (InputIterator1 first1, InputIterator1 last1, MaskIterator mask_first, InputIterator2 first2, typename std::iterator_traits< MaskIterator >::value_type value=typename std::iterator_traits< MaskIterator >::value_type(1)) |
Computes the Linfinite distance of two ranges according to a mask sequence : 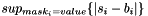 . More... . More... | |
| template<typename Real , typename InputIterator1 , typename InputIterator2 , typename Predicate > | |
| Real | Linf_distance_if (InputIterator1 first1, InputIterator1 last1, InputIterator2 first2, Predicate pred) |
| Computes the Linfinite distance of two ranges according to a Predicate. More... | |
| template<typename Real , typename InputIterator1 , typename InputIterator2 > | |
| Real | KullbackLeibler_distance (InputIterator1 first1, InputIterator1 last1, InputIterator2 first2) |
Computes the Kullback-Leibler "distance" of two ranges : 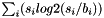 . More... . More... | |
| template<typename Real , typename InputIterator1 , typename InputIterator2 , typename MaskIterator > | |
| Real | KullbackLeibler_distance_mask (InputIterator1 first1, InputIterator1 last1, MaskIterator mask_first, InputIterator2 first2, typename std::iterator_traits< MaskIterator >::value_type value=typename std::iterator_traits< MaskIterator >::value_type(1)) |
Computes the Kullback-Leibler "distance" of two ranges according to a mask sequence : 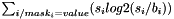 . More... . More... | |
| template<typename Real , typename InputIterator1 , typename InputIterator2 , typename Predicate > | |
| Real | KullbackLeibler_distance_if (InputIterator1 first1, InputIterator1 last1, InputIterator2 first2, Predicate pred) |
| Computes the Kullback-Leibler "distance" of two ranges according to a Predicate. More... | |
| template<typename Real , typename InputIterator1 , typename InputIterator2 > | |
| Real | Chi2_distance (InputIterator1 first1, InputIterator1 last1, InputIterator2 first2) |
Computes the Chi2 "distance" of two ranges : 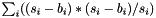 . More... . More... | |
| template<typename Real , typename InputIterator1 , typename InputIterator2 , typename MaskIterator > | |
| Real | Chi2_distance_mask (InputIterator1 first1, InputIterator1 last1, MaskIterator mask_first, InputIterator2 first2, typename std::iterator_traits< MaskIterator >::value_type value=typename std::iterator_traits< MaskIterator >::value_type(1)) |
Computes the Chi2 "distance" of two ranges according to a mask sequence : 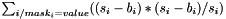 . More... . More... | |
| template<typename Real , typename InputIterator1 , typename InputIterator2 , typename Predicate > | |
| Real | Chi2_distance_if (InputIterator1 first1, InputIterator1 last1, InputIterator2 first2, Predicate pred) |
| Computes the Chi2 "distance" of two ranges according to a Predicate. More... | |
| template<typename Value_T , typename InputIterator1 , typename InputIterator2 > | |
| Value_T | psnr (InputIterator1 first1, InputIterator1 last1, InputIterator2 first2, Value_T d=static_cast< Value_T >(255)) |
| template<typename Value_T , typename InputIterator1 , typename InputIterator2 , typename MaskIterator > | |
| Value_T | psnr_mask (InputIterator1 first1, InputIterator1 last1, MaskIterator mask1, InputIterator2 first2, typename std::iterator_traits< MaskIterator >::value_type value=typename std::iterator_traits< MaskIterator >::value_type(1), Value_T d=static_cast< Value_T >(255)) |
| template<typename Value_T , typename InputIterator1 , typename InputIterator2 , typename Predicate > | |
| Value_T | psnr_if (InputIterator1 first1, InputIterator1 last1, InputIterator2 first2, Predicate pred, Value_T d=static_cast< Value_T >(255)) |
| template<typename Real , typename InputIterator1 , typename InputIterator2 > | |
| Real | SSIM (InputIterator1 first1, InputIterator1 last1, InputIterator2 first2, Real d=static_cast< Real >(255)) |
| Computes the Structural SIMilarity (SSIM) beetween two data ranges
where. More... | |
| template<typename Real , typename InputIterator1 , typename InputIterator2 , typename MaskIterator > | |
| Real | SSIM_mask (InputIterator1 first1, InputIterator1 last1, MaskIterator maskFirst, InputIterator2 first2, typename std::iterator_traits< MaskIterator >::value_type value=typename std::iterator_traits< MaskIterator >::value_type(1), Real d=static_cast< Real >(255)) |
| Computes the structural similarity beetween two data ranges according to a mask range
where. More... | |
| template<typename Real , typename InputIterator1 , typename InputIterator2 , typename Predicate > | |
| Real | SSIM_if (InputIterator1 first1, InputIterator1 last1, InputIterator2 first2, Predicate pred, Real d=255) |
| Computes the Sructural SIMilarity (SSIM) beetween two data ranges according to a predicate
where. More... | |
1d convolutions | |
| template<typename SrcIter , typename KernelIter , typename ResIter > | |
| void | valid_convolution (SrcIter first, SrcIter last, KernelIter kernel_first, KernelIter kernel_last, std::size_t ksize_left, std::size_t ksize_right, ResIter result) |
| Computes the valid convolution of signal by a 1d-kernel. More... | |
| template<typename SrcIter , typename KernelIter , typename ResIter > | |
| void | full_convolution (SrcIter first, SrcIter last, KernelIter kernel_first, KernelIter kernel_last, ResIter result) |
| Computes the full convolution of signal by a 1d-kernel. More... | |
| template<typename SrcIter , typename KernelIter , typename ResIter > | |
| void | same_convolution (SrcIter first, SrcIter last, KernelIter kernel_first, KernelIter kernel_last, std::size_t ksize_left, std::size_t ksize_right, ResIter result, slip::BORDER_TREATMENT bt=slip::BORDER_TREATMENT_ZERO_PADDED) |
| Computes the same convolution of signal by a 1d-kernel. More... | |
| template<typename SrcIter , typename KernelIter , typename ResIter > | |
| void | same_convolution (SrcIter first, SrcIter last, KernelIter kernel_first, KernelIter kernel_last, ResIter result, slip::BORDER_TREATMENT bt=slip::BORDER_TREATMENT_ZERO_PADDED) |
| Computes the same convolution of signal by a symmetric 1d-kernel support. More... | |
| template<typename Vector1 , typename Vector2 , typename Vector3 > | |
| void | same_convolution (const Vector1 &Signal, const Vector2 &Kernel, Vector3 &Result, slip::BORDER_TREATMENT bt=slip::BORDER_TREATMENT_ZERO_PADDED) |
| Computes the same convolution of signal by a symmetric 1d-kernel. More... | |
| template<typename RandomAccessIterator1 , typename RandomAccessIterator2 , typename RandomAccessIterator3 > | |
| void | fft_circular_convolution (RandomAccessIterator1 first, RandomAccessIterator1 last, RandomAccessIterator2 first2, RandomAccessIterator2 last2, RandomAccessIterator3 conv_first, RandomAccessIterator3 conv_last) |
| Computes the FFT circular convolution. More... | |
| template<typename RandomAccessIterator1 , typename RandomAccessIterator2 , typename RandomAccessIterator3 > | |
| void | fft_convolution (RandomAccessIterator1 first, RandomAccessIterator1 last, RandomAccessIterator2 first2, RandomAccessIterator2 last2, RandomAccessIterator3 conv_first, RandomAccessIterator3 conv_last) |
| Computes the FFT convolution. More... | |
| template<typename Vector1 , typename Vector2 , typename Vector3 > | |
| void | fft_convolution (const Vector1 &Signal, const Vector2 &Kernel, Vector3 &Result) |
| Computes the fft convolution of signal by a symmetric 1d-kernel. More... | |
2d convolutions | |
| template<typename RandomAccessIterator2d1 , typename KernelIter1 , typename KernelIter2 , typename RandomAccessIterator2d2 > | |
| void | separable_convolution2d (RandomAccessIterator2d1 I_up, RandomAccessIterator2d1 I_bot, KernelIter1 k1_first, KernelIter1 k1_last, std::size_t ksize_left1, std::size_t ksize_right1, slip::BORDER_TREATMENT bt1, KernelIter2 k2_first, KernelIter2 k2_last, std::size_t ksize_left2, std::size_t ksize_right2, slip::BORDER_TREATMENT bt2, RandomAccessIterator2d2 R_up) |
| Computes the separable convolution of a 2d signal by two asymmetric 1d-kernels support. More... | |
| template<typename RandomAccessIterator2d1 , typename KernelIter1 , typename KernelIter2 , typename RandomAccessIterator2d2 > | |
| void | separable_convolution2d (RandomAccessIterator2d1 I_up, RandomAccessIterator2d1 I_bot, KernelIter1 k1_first, KernelIter1 k1_last, KernelIter2 k2_first, KernelIter2 k2_last, RandomAccessIterator2d2 R_up, slip::BORDER_TREATMENT bt=slip::BORDER_TREATMENT_ZERO_PADDED) |
| Computes the separable convolution of a 2d signal by two symmetric 1d-kernels support. More... | |
| template<typename Container1 , typename Kernel1 , typename Kernel2 , typename Container2 > | |
| void | separable_convolution2d (const Container1 &Signal, const Kernel1 &kernel1, const Kernel2 &kernel2, Container2 &Result, slip::BORDER_TREATMENT bt=slip::BORDER_TREATMENT_ZERO_PADDED) |
| Computes the separable convolution of 2d signal by 2 symmetric 1d-kernel support. More... | |
| template<typename RandomAccessIterator2d1 , typename KernelIter1 , typename KernelIter2 > | |
| void | separable_convolution2d (RandomAccessIterator2d1 I_up, RandomAccessIterator2d1 I_bot, KernelIter1 k1_first, KernelIter1 k1_last, std::size_t ksize_left1, std::size_t ksize_right1, slip::BORDER_TREATMENT bt1, KernelIter2 k2_first, KernelIter2 k2_last, std::size_t ksize_left2, std::size_t ksize_right2, slip::BORDER_TREATMENT bt2) |
| Computes the in-place separable convolution of a 2d signal by two asymmetric 1d-kernels support. More... | |
| template<typename RandomAccessIterator2d1 , typename KernelIter1 , typename KernelIter2 , typename RandomAccessIterator2d2 > | |
| void | separable_fft_convolution2d (RandomAccessIterator2d1 I_up, RandomAccessIterator2d1 I_bot, KernelIter1 k1_first, KernelIter1 k1_last, KernelIter2 k2_first, KernelIter2 k2_last, RandomAccessIterator2d2 R_up) |
| Computes the separable 2d convolution of signal using the fft algorithm. More... | |
| template<typename Container1 , typename Kernel1 , typename Kernel2 , typename Container2 > | |
| void | separable_fft_convolution2d (const Container1 &Signal, const Kernel1 &kernel1, const Kernel2 &kernel2, Container2 &Result) |
| Computes the fft convolution of a 2d signal. More... | |
| template<typename SrcIter2d , typename KernelIter2d , typename ResIter2d > | |
| void | valid_convolution2d (SrcIter2d S_up, SrcIter2d S_bot, KernelIter2d kernel_up, KernelIter2d kernel_bot, std::size_t ksize_left, std::size_t ksize_right, std::size_t ksize_up, std::size_t ksize_bot, ResIter2d R_up, ResIter2d R_bot) |
| Computes the valid convolution of 2d signal by a 2d-kernel. More... | |
| template<typename SrcIter2d , typename KernelIter2d , typename ResIter2d > | |
| void | same_convolution2d (SrcIter2d S_up, SrcIter2d S_bot, KernelIter2d kernel_up, KernelIter2d kernel_bot, int ksize_left, int ksize_right, int ksize_up, int ksize_bot, ResIter2d R_up, ResIter2d R_bot, slip::BORDER_TREATMENT bt=slip::BORDER_TREATMENT_ZERO_PADDED) |
| Computes the same convolution of 2d signal by a 2d-kernel. More... | |
| template<typename SrcIter2d , typename KernelIter2d , typename ResIter2d > | |
| void | same_convolution2d (SrcIter2d S_up, SrcIter2d S_bot, KernelIter2d kernel_up, KernelIter2d kernel_bot, ResIter2d R_up, ResIter2d R_bot, slip::BORDER_TREATMENT bt=slip::BORDER_TREATMENT_ZERO_PADDED) |
| Computes the same convolution of 2d signal by a symmetric 2d-kernel support. More... | |
| template<typename Container2d1 , typename Kernel2d , typename Container2d2 > | |
| void | same_convolution2d (const Container2d1 &Signal, const Kernel2d &Kernel, Container2d2 &Result, slip::BORDER_TREATMENT bt) |
| Computes the same convolution of 2d signal by a symmetric 2d-kernel. More... | |
| template<typename SrcIter2d , typename KernelIter2d , typename ResIter2d > | |
| void | full_convolution2d (SrcIter2d S_up, SrcIter2d S_bot, KernelIter2d kernel_up, KernelIter2d kernel_bot, ResIter2d R_up, ResIter2d R_bot) |
| Computes the full convolution of 2d signal by a 2d-kernel. More... | |
| template<typename InputIterator2d1 , typename InputIterator2d2 , typename OutputIterator2d > | |
| void | fft_convolution2d (InputIterator2d1 in1_upper_left, InputIterator2d1 in1_bottom_right, InputIterator2d2 in2_upper_left, InputIterator2d2 in2_bottom_right, OutputIterator2d out_upper_left, OutputIterator2d out_bottom_right) |
| Computes the standard crosscorrelation between two 2D sequences using fft2d. More... | |
| template<typename Container2d1 , typename Kernel2d , typename Container2d2 > | |
| void | fft_convolution2d (const Container2d1 &Signal, const Kernel2d &Kernel, Container2d2 &Result) |
| Computes the convolution of a 2d signal using the fft2d. More... | |
3d convolutions | |
| template<typename RandomAccessIterator3d1 , typename KernelIter1 , typename KernelIter2 , typename KernelIter3 , typename RandomAccessIterator3d2 > | |
| void | separable_convolution3d (RandomAccessIterator3d1 I_up, RandomAccessIterator3d1 I_bot, KernelIter1 k1_first, KernelIter1 k1_last, std::size_t ksize_left1, std::size_t ksize_right1, slip::BORDER_TREATMENT bt1, KernelIter2 k2_first, KernelIter2 k2_last, std::size_t ksize_left2, std::size_t ksize_right2, slip::BORDER_TREATMENT bt2, KernelIter3 k3_first, KernelIter3 k3_last, std::size_t ksize_left3, std::size_t ksize_right3, slip::BORDER_TREATMENT bt3, RandomAccessIterator3d2 R_up) |
| Computes the separable convolution of a 3d signal by 3 asymmetric 1d-kernels. More... | |
| template<typename RandomAccessIterator3d1 , typename KernelIter1 , typename KernelIter2 , typename KernelIter3 , typename RandomAccessIterator3d2 > | |
| void | separable_convolution3d (RandomAccessIterator3d1 I_up, RandomAccessIterator3d1 I_bot, KernelIter1 k1_first, KernelIter1 k1_last, KernelIter2 k2_first, KernelIter2 k2_last, KernelIter3 k3_first, KernelIter3 k3_last, RandomAccessIterator3d2 R_up, slip::BORDER_TREATMENT bt=slip::BORDER_TREATMENT_ZERO_PADDED) |
| Computes the separable convolution of a 3d signal by 3 symmetric 1d-kernels. More... | |
| template<typename Container1 , typename Kernel1 , typename Kernel2 , typename Kernel3 , typename Container2 > | |
| void | separable_convolution3d (const Container1 &Signal, const Kernel1 &kernel1, const Kernel2 &kernel2, const Kernel3 &kernel3, Container2 &Result, slip::BORDER_TREATMENT bt=slip::BORDER_TREATMENT_ZERO_PADDED) |
| Computes the separable convolution of 3d signal by a 3 1d-kernel. More... | |
| template<typename RandomAccessIterator3d1 , typename KernelIter1 , typename KernelIter2 , typename KernelIter3 > | |
| void | separable_convolution3d (RandomAccessIterator3d1 I_up, RandomAccessIterator3d1 I_bot, KernelIter1 k1_first, KernelIter1 k1_last, std::size_t ksize_left1, std::size_t ksize_right1, slip::BORDER_TREATMENT bt1, KernelIter2 k2_first, KernelIter2 k2_last, std::size_t ksize_left2, std::size_t ksize_right2, slip::BORDER_TREATMENT bt2, KernelIter3 k3_first, KernelIter3 k3_last, std::size_t ksize_left3, std::size_t ksize_right3, slip::BORDER_TREATMENT bt3) |
| Computes the in-place separable convolution of a 3d signal by 3 asymmetric 1d-kernels. More... | |
| template<typename RandomAccessIterator3d1 , typename KernelIter1 , typename KernelIter2 , typename KernelIter3 , typename RandomAccessIterator3d2 > | |
| void | separable_fft_convolution3d (RandomAccessIterator3d1 I_up, RandomAccessIterator3d1 I_bot, KernelIter1 k1_first, KernelIter1 k1_last, KernelIter2 k2_first, KernelIter2 k2_last, KernelIter3 k3_first, KernelIter3 k3_last, RandomAccessIterator3d2 R_up) |
| Computes the separable 3d convolution of signal using the fft algorithm. More... | |
| template<typename Container1 , typename Kernel1 , typename Kernel2 , typename Kernel3 , typename Container2 > | |
| void | separable_fft_convolution3d (const Container1 &Signal, const Kernel1 &kernel1, const Kernel2 &kernel2, const Kernel3 &kernel3, Container2 &Result) |
| Computes the separable fft convolution of 3d signal by 3 1d-kernel. More... | |
| template<typename InputIterator3d1 , typename InputIterator3d2 , typename OutputIterator3d > | |
| void | fft_convolution3d (InputIterator3d1 in1_front_upper_left, InputIterator3d1 in1_back_bottom_right, InputIterator3d2 in2_front_upper_left, InputIterator3d2 in2_back_bottom_right, OutputIterator3d out_front_upper_left, OutputIterator3d out_back_bottom_right) |
| Computes the convolution of two 3D sequences using fft3d. More... | |
| template<typename Container3d1 , typename Kernel3d , typename Container3d2 > | |
| void | fft_convolution3d (const Container3d1 &Signal, const Kernel3d &Kernel, Container3d2 &Result) |
| Computes the convolution of a 3d signal using the fft3d. More... | |
| template<typename InputIterator3d1 , typename InputIterator3d2 , typename OutputIterator3d > | |
| void | fft_convolution3d_same (InputIterator3d1 in1_front_upper_left, InputIterator3d1 in1_back_bottom_right, InputIterator3d2 in2_front_upper_left, InputIterator3d2 in2_back_bottom_right, OutputIterator3d out_front_upper_left, OutputIterator3d out_back_bottom_right) |
| Computes the convolution between two 3D sequences using fft3d. More... | |
| template<typename SrcIter3d , typename KernelIter3d , typename ResIter3d > | |
| void | valid_convolution3d (SrcIter3d S_up, SrcIter3d S_bot, KernelIter3d kernel_up, KernelIter3d kernel_bot, std::size_t ksize_front, std::size_t ksize_back, std::size_t ksize_left, std::size_t ksize_right, std::size_t ksize_up, std::size_t ksize_bot, ResIter3d R_up, ResIter3d R_bot) |
| Computes the valid convolution of 3d signal by a 3d-kernel. More... | |
crosscorrelations between two ranges | |
| template<typename T , typename InputIterator1 , typename InputIterator2 > | |
| T | std_crosscorrelation (InputIterator1 first, InputIterator1 last, InputIterator2 first2) |
Computes the standard crosscorrelation between two sequences: 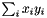 . Multiplies successive elements from the two ranges and adds each product into the accumulated value using operator+(). The values in the ranges are processed in order. More... . Multiplies successive elements from the two ranges and adds each product into the accumulated value using operator+(). The values in the ranges are processed in order. More... | |
| template<typename T , typename InputIterator1 , typename InputIterator2 , typename MaskIterator > | |
| T | std_crosscorrelation_mask (InputIterator1 first1, InputIterator1 last1, MaskIterator mask_first, InputIterator2 first2, typename std::iterator_traits< MaskIterator >::value_type value=typename std::iterator_traits< MaskIterator >::value_type(1)) |
Computes the standard crosscorrelation between two sequences according to a mask sequence 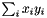 . Multiplies successive elements accordind to a mask sequence from the two ranges and adds each product into the accumulated value using operator+(). The values in the ranges are processed in order. More... . Multiplies successive elements accordind to a mask sequence from the two ranges and adds each product into the accumulated value using operator+(). The values in the ranges are processed in order. More... | |
| template<typename T , typename InputIterator1 , typename InputIterator2 , typename Predicate > | |
| T | std_crosscorrelation_if (InputIterator1 first1, InputIterator1 last1, InputIterator2 first2, Predicate pred) |
Computes the standard crosscorrelation between two sequences according to a Predicate. 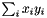 . More... . More... | |
| template<typename T , typename InputIterator1 , typename InputIterator2 > | |
| T | cc (InputIterator1 first, InputIterator1 last, InputIterator2 first2) |
Computes the standard crosscorrelation between two sequences: 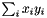 . Multiplies successive elements from the two ranges and adds each product into the accumulated value using operator+(). The values in the ranges are processed in order. More... . Multiplies successive elements from the two ranges and adds each product into the accumulated value using operator+(). The values in the ranges are processed in order. More... | |
| template<typename T , typename InputIterator1 , typename InputIterator2 , typename MaskIterator > | |
| T | cc_mask (InputIterator1 first1, InputIterator1 last1, MaskIterator mask_first, InputIterator2 first2, typename std::iterator_traits< MaskIterator >::value_type value=typename std::iterator_traits< MaskIterator >::value_type(1)) |
Computes the standard crosscorrelation between two sequences according to a mask sequence 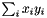 . Multiplies successive elements from the two ranges accordind to a mask sequence and adds each product according to the mask range into the accumulated value using operator+(). The values in the ranges are processed in order. More... . Multiplies successive elements from the two ranges accordind to a mask sequence and adds each product according to the mask range into the accumulated value using operator+(). The values in the ranges are processed in order. More... | |
| template<typename T , typename InputIterator1 , typename InputIterator2 , typename Predicate > | |
| T | cc_if (InputIterator1 first1, InputIterator1 last1, InputIterator2 first2, Predicate pred) |
Computes the standard crosscorrelation between two sequences according to a Predicate. 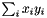 . More... . More... | |
| template<typename Real , typename InputIterator1 , typename InputIterator2 > | |
| Real | centered_crosscorrelation (InputIterator1 first, InputIterator1 last, InputIterator2 first2, typename std::iterator_traits< InputIterator1 >::value_type mean1=typename std::iterator_traits< InputIterator1 >::value_type(), typename std::iterator_traits< InputIterator1 >::value_type mean2=typename std::iterator_traits< InputIterator2 >::value_type()) |
Computes the centered crosscorrelation between two sequences: 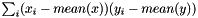 . More... . More... | |
| template<typename Real , typename InputIterator1 , typename InputIterator2 , typename MaskIterator > | |
| Real | centered_crosscorrelation_mask (InputIterator1 first1, InputIterator1 last1, MaskIterator mask_first, InputIterator2 first2, typename std::iterator_traits< InputIterator1 >::value_type mean1=typename std::iterator_traits< InputIterator1 >::value_type(), typename std::iterator_traits< InputIterator1 >::value_type mean2=typename std::iterator_traits< InputIterator2 >::value_type(), typename std::iterator_traits< MaskIterator >::value_type value=typename std::iterator_traits< MaskIterator >::value_type(1)) |
Computes the centered crosscorrelation between two sequences according to a mask sequence 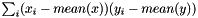 . More... . More... | |
| template<typename Real , typename InputIterator1 , typename InputIterator2 , typename Predicate > | |
| Real | centered_crosscorrelation_if (InputIterator1 first1, InputIterator1 last1, InputIterator2 first2, Predicate pred, typename std::iterator_traits< InputIterator1 >::value_type mean1=typename std::iterator_traits< InputIterator1 >::value_type(), typename std::iterator_traits< InputIterator1 >::value_type mean2=typename std::iterator_traits< InputIterator2 >::value_type()) |
Computes the standard crosscorrelation between two sequences according to a Predicate: 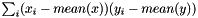 . More... . More... | |
| template<typename Real , typename InputIterator1 , typename InputIterator2 > | |
| Real | ccc (InputIterator1 first, InputIterator1 last, InputIterator2 first2, typename std::iterator_traits< InputIterator1 >::value_type mean1=typename std::iterator_traits< InputIterator1 >::value_type(), typename std::iterator_traits< InputIterator1 >::value_type mean2=typename std::iterator_traits< InputIterator2 >::value_type()) |
Computes the centered crosscorrelation between two sequences: 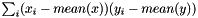 . More... . More... | |
| template<typename Real , typename InputIterator1 , typename InputIterator2 , typename MaskIterator > | |
| Real | ccc_mask (InputIterator1 first1, InputIterator1 last1, MaskIterator mask_first, InputIterator2 first2, typename std::iterator_traits< InputIterator1 >::value_type mean1=typename std::iterator_traits< InputIterator1 >::value_type(), typename std::iterator_traits< InputIterator1 >::value_type mean2=typename std::iterator_traits< InputIterator2 >::value_type(), typename std::iterator_traits< MaskIterator >::value_type value=typename std::iterator_traits< MaskIterator >::value_type(1)) |
Computes the centered crosscorrelation between two sequences according to a mask sequence 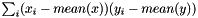 . More... . More... | |
| template<typename Real , typename InputIterator1 , typename InputIterator2 , typename Predicate > | |
| Real | ccc_if (InputIterator1 first1, InputIterator1 last1, InputIterator2 first2, Predicate pred, typename std::iterator_traits< InputIterator1 >::value_type mean1=typename std::iterator_traits< InputIterator1 >::value_type(), typename std::iterator_traits< InputIterator1 >::value_type mean2=typename std::iterator_traits< InputIterator2 >::value_type()) |
Computes the standard crosscorrelation between two sequences according to a Predicate: 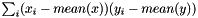 . More... . More... | |
| template<typename Real , typename InputIterator1 , typename InputIterator2 > | |
| Real | pseudo_normalized_crosscorrelation (InputIterator1 first, InputIterator1 last, InputIterator2 first2, typename std::iterator_traits< InputIterator1 >::value_type mean1=typename std::iterator_traits< InputIterator1 >::value_type(), typename std::iterator_traits< InputIterator1 >::value_type mean2=typename std::iterator_traits< InputIterator2 >::value_type()) |
Computes the pseudo normalized crosscorrelation between two sequences: 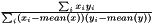 . More... . More... | |
| template<typename Real , typename InputIterator1 , typename InputIterator2 , typename MaskIterator > | |
| Real | pseudo_normalized_crosscorrelation_mask (InputIterator1 first1, InputIterator1 last1, MaskIterator mask_first, InputIterator2 first2, typename std::iterator_traits< InputIterator1 >::value_type mean1=typename std::iterator_traits< InputIterator1 >::value_type(), typename std::iterator_traits< InputIterator1 >::value_type mean2=typename std::iterator_traits< InputIterator2 >::value_type(), typename std::iterator_traits< MaskIterator >::value_type value=typename std::iterator_traits< MaskIterator >::value_type(1)) |
Computes the pseudo normalized crosscorrelation between two sequences according to a mask sequence : 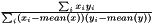 . More... . More... | |
| template<typename Real , typename InputIterator1 , typename InputIterator2 , typename Predicate > | |
| Real | pseudo_normalized_crosscorrelation_if (InputIterator1 first1, InputIterator1 last1, InputIterator2 first2, Predicate pred, typename std::iterator_traits< InputIterator1 >::value_type mean1=typename std::iterator_traits< InputIterator1 >::value_type(), typename std::iterator_traits< InputIterator1 >::value_type mean2=typename std::iterator_traits< InputIterator2 >::value_type()) |
Computes the standard pseudo normalized crosscorrelation between two sequences according to a Predicate. 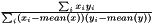 . More... . More... | |
| template<typename Real , typename InputIterator1 , typename InputIterator2 > | |
| Real | pncc (InputIterator1 first, InputIterator1 last, InputIterator2 first2, typename std::iterator_traits< InputIterator1 >::value_type mean1=typename std::iterator_traits< InputIterator1 >::value_type(), typename std::iterator_traits< InputIterator1 >::value_type mean2=typename std::iterator_traits< InputIterator2 >::value_type()) |
Computes the pseudo normalized crosscorrelation between two sequences: 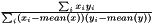 . More... . More... | |
| template<typename Real , typename InputIterator1 , typename InputIterator2 , typename MaskIterator > | |
| Real | pncc_mask (InputIterator1 first1, InputIterator1 last1, MaskIterator mask_first, InputIterator2 first2, typename std::iterator_traits< InputIterator1 >::value_type mean1=typename std::iterator_traits< InputIterator1 >::value_type(), typename std::iterator_traits< InputIterator1 >::value_type mean2=typename std::iterator_traits< InputIterator2 >::value_type(), typename std::iterator_traits< MaskIterator >::value_type value=typename std::iterator_traits< MaskIterator >::value_type(1)) |
Computes the pseudo normalized crosscorrelation between two sequences according to a mask sequence : 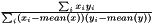 . More... . More... | |
| template<typename Real , typename InputIterator1 , typename InputIterator2 , typename Predicate > | |
| Real | pncc_if (InputIterator1 first1, InputIterator1 last1, InputIterator2 first2, Predicate pred, typename std::iterator_traits< InputIterator1 >::value_type mean1=typename std::iterator_traits< InputIterator1 >::value_type(), typename std::iterator_traits< InputIterator1 >::value_type mean2=typename std::iterator_traits< InputIterator2 >::value_type()) |
Computes the standard pseudo normalized crosscorrelation between two sequences according to a Predicate. 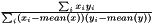 . More... . More... | |
| template<typename Real , typename InputIterator1 , typename InputIterator2 > | |
| Real | normalized_crosscorrelation (InputIterator1 first, InputIterator1 last, InputIterator2 first2, typename std::iterator_traits< InputIterator1 >::value_type mean1=typename std::iterator_traits< InputIterator1 >::value_type(), typename std::iterator_traits< InputIterator1 >::value_type mean2=typename std::iterator_traits< InputIterator2 >::value_type()) |
Computes the standard normalized crosscorrelation between two sequences: 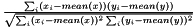 . More... . More... | |
| template<typename Real , typename InputIterator1 , typename InputIterator2 , typename MaskIterator > | |
| Real | normalized_crosscorrelation_mask (InputIterator1 first1, InputIterator1 last1, MaskIterator mask_first, InputIterator2 first2, typename std::iterator_traits< InputIterator1 >::value_type mean1=typename std::iterator_traits< InputIterator1 >::value_type(), typename std::iterator_traits< InputIterator1 >::value_type mean2=typename std::iterator_traits< InputIterator2 >::value_type(), typename std::iterator_traits< MaskIterator >::value_type value=typename std::iterator_traits< MaskIterator >::value_type(1)) |
Computes the standard normalized crosscorrelation between two sequences according to a mask sequence 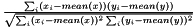 . More... . More... | |
| template<typename Real , typename InputIterator1 , typename InputIterator2 , typename Predicate > | |
| Real | normalized_crosscorrelation_if (InputIterator1 first1, InputIterator1 last1, InputIterator2 first2, Predicate pred, typename std::iterator_traits< InputIterator1 >::value_type mean1=typename std::iterator_traits< InputIterator1 >::value_type(), typename std::iterator_traits< InputIterator1 >::value_type mean2=typename std::iterator_traits< InputIterator2 >::value_type()) |
Computes the standard normalized crosscorrelation between two sequences according to a Predicate: ** 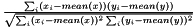 . More... . More... | |
| template<typename Real , typename InputIterator1 , typename InputIterator2 > | |
| Real | ncc (InputIterator1 first, InputIterator1 last, InputIterator2 first2, typename std::iterator_traits< InputIterator1 >::value_type mean1=typename std::iterator_traits< InputIterator1 >::value_type(), typename std::iterator_traits< InputIterator1 >::value_type mean2=typename std::iterator_traits< InputIterator2 >::value_type()) |
Computes the standard normalized crosscorrelation between two sequences: 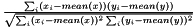 . More... . More... | |
| template<typename Real , typename InputIterator1 , typename InputIterator2 , typename MaskIterator > | |
| Real | ncc_mask (InputIterator1 first1, InputIterator1 last1, MaskIterator mask_first, InputIterator2 first2, typename std::iterator_traits< InputIterator1 >::value_type mean1=typename std::iterator_traits< InputIterator1 >::value_type(), typename std::iterator_traits< InputIterator1 >::value_type mean2=typename std::iterator_traits< InputIterator2 >::value_type(), typename std::iterator_traits< MaskIterator >::value_type value=typename std::iterator_traits< MaskIterator >::value_type(1)) |
Computes the standard normalized crosscorrelation between two sequences according to a mask sequence 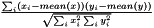 . More... . More... | |
| template<typename Real , typename InputIterator1 , typename InputIterator2 , typename Predicate > | |
| Real | ncc_if (InputIterator1 first1, InputIterator1 last1, InputIterator2 first2, Predicate pred, typename std::iterator_traits< InputIterator1 >::value_type mean1=typename std::iterator_traits< InputIterator1 >::value_type(), typename std::iterator_traits< InputIterator1 >::value_type mean2=typename std::iterator_traits< InputIterator2 >::value_type()) |
Computes the standard normalized crosscorrelation between two sequences according to a Predicate: 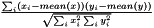 . More... . More... | |
autocorrelations and autocovariance algorithms | |
| template<typename RandomAccessIterator1 , typename RandomAccessIterator2 > | |
| void | autocorrelation_full (RandomAccessIterator1 first, RandomAccessIterator1 last, RandomAccessIterator2 auto_first, RandomAccessIterator2 auto_last) |
| Computes the autocorrelations from lag -(last-first) to (last-first) of a range [first,last). More... | |
| template<typename RandomAccessIterator1 , typename RandomAccessIterator2 > | |
| void | autocorrelation (RandomAccessIterator1 first, RandomAccessIterator1 last, RandomAccessIterator2 auto_first, RandomAccessIterator2 auto_last) |
| Computes the autocorrelations from lag -(last-first) to (last-first) of a range [first,last). More... | |
| template<typename RandomAccessIterator1 , typename RandomAccessIterator2 > | |
| void | biased_autocorrelation (RandomAccessIterator1 first, RandomAccessIterator1 last, RandomAccessIterator2 auto_first, RandomAccessIterator2 auto_last) |
| Computes the biased autocorrelations from lag -(last-first) to (last-first) of a range [first,last). More... | |
| template<typename RandomAccessIterator1 , typename RandomAccessIterator2 > | |
| void | unbiased_autocorrelation (RandomAccessIterator1 first, RandomAccessIterator1 last, RandomAccessIterator2 auto_first, RandomAccessIterator2 auto_last) |
| Computes the unbiased autocorrelations from lag -(last-first) to (last-first) of a range [first,last). More... | |
| template<typename RandomAccessIterator1 , typename RandomAccessIterator2 > | |
| void | autocovariance (RandomAccessIterator1 first, RandomAccessIterator1 last, RandomAccessIterator2 auto_first, RandomAccessIterator2 auto_last) |
| Computes the autocovariance from lag -(last-first) to 0 of a range [first,last). More... | |
| template<typename RandomAccessIterator1 , typename RandomAccessIterator2 > | |
| void | biased_autocovariance (RandomAccessIterator1 first, RandomAccessIterator1 last, RandomAccessIterator2 auto_first, RandomAccessIterator2 auto_last) |
| Computes the biased autocovariance from lag -(last-first) to 0 of a range [first,last). More... | |
| template<typename RandomAccessIterator1 , typename RandomAccessIterator2 > | |
| void | unbiased_autocovariance (RandomAccessIterator1 first, RandomAccessIterator1 last, RandomAccessIterator2 auto_first, RandomAccessIterator2 auto_last) |
| Computes the unbiased autocovariance from lag -(last-first) to 0 of a range [first,last). More... | |
| template<typename RandomAccessIterator , typename Matrix > | |
| void | biased_autocorrelation_matrix (RandomAccessIterator first, RandomAccessIterator last, Matrix &A) |
| Constructs the biased autocorrelation matrix from given a range. More... | |
| template<typename RandomAccessIterator , typename Matrix > | |
| void | biased_autocovariance_matrix (RandomAccessIterator first, RandomAccessIterator last, Matrix &A) |
| Constructs the biased autocorrelation matrix from given a range. More... | |
crosscorrelation map algorithms | |
| template<typename Real , typename InputIterator2d1 , typename InputIterator2d2 , typename OutputIterator2d > | |
| void | crosscorrelation2d (InputIterator2d1 in1_upper_left, InputIterator2d1 in1_bottom_right, InputIterator2d2 in2_upper_left, InputIterator2d2 in2_bottom_right, OutputIterator2d out_upper_left, OutputIterator2d out_bottom_right, CROSSCORRELATION_TYPE t) |
| Computes the crosscorrelation between two Images. More... | |
| template<typename Real , typename InputIterator2d1 , typename InputIterator2d2 , typename OutputIterator2d > | |
| void | std_crosscorrelation2d (InputIterator2d1 in1_upper_left, InputIterator2d1 in1_bottom_right, InputIterator2d2 in2_upper_left, InputIterator2d2 in2_bottom_right, OutputIterator2d out_upper_left, OutputIterator2d out_bottom_right) |
| Computes the standard crosscorrelation between two Images. More... | |
| template<typename Real , typename InputIterator2d1 , typename InputIterator2d2 , typename OutputIterator2d > | |
| void | centered_crosscorrelation2d (InputIterator2d1 in1_upper_left, InputIterator2d1 in1_bottom_right, InputIterator2d2 in2_upper_left, InputIterator2d2 in2_bottom_right, OutputIterator2d out_upper_left, OutputIterator2d out_bottom_right) |
| Computes the centered crosscorrelation between two Images. More... | |
| template<typename Real , typename InputIterator2d1 , typename InputIterator2d2 , typename OutputIterator2d > | |
| void | pseudo_normalized_crosscorrelation2d (InputIterator2d1 in1_upper_left, InputIterator2d1 in1_bottom_right, InputIterator2d2 in2_upper_left, InputIterator2d2 in2_bottom_right, OutputIterator2d out_upper_left, OutputIterator2d out_bottom_right) |
| Computes the pseudo normalized crosscorrelation between two Images. More... | |
| template<typename Real , typename InputIterator2d1 , typename InputIterator2d2 , typename OutputIterator2d > | |
| void | normalized_crosscorrelation2d (InputIterator2d1 in1_upper_left, InputIterator2d1 in1_bottom_right, InputIterator2d2 in2_upper_left, InputIterator2d2 in2_bottom_right, OutputIterator2d out_upper_left, OutputIterator2d out_bottom_right) |
| Computes the normalized crosscorrelation between two Images. More... | |
fft crosscorrelation algorithms | |
| template<typename InputIterator1 , typename InputIterator2 , typename OutputIterator > | |
| void | fft_crosscorrelation (InputIterator1 first, InputIterator1 last, InputIterator2 first2, InputIterator2 last2, OutputIterator result_first, OutputIterator result_last) |
| Computes the standard crosscorrelation between two sequences using fft. More... | |
| template<typename InputIterator1 , typename InputIterator2 , typename OutputIterator > | |
| void | fft_crosscorrelation_same (InputIterator1 first, InputIterator1 last, InputIterator2 first2, InputIterator2 last2, OutputIterator result_first, OutputIterator result_last) |
| Computes the FFT central part of the crosscorrelation. More... | |
| template<typename RandomAccessIterator1 , typename RandomAccessIterator2 , typename RandomAccessIterator3 > | |
| void | fft_circular_crosscorrelation (RandomAccessIterator1 first, RandomAccessIterator1 last, RandomAccessIterator2 first2, RandomAccessIterator2 last2, RandomAccessIterator3 result_first, RandomAccessIterator3 result_last) |
| Computes the FFT circular crosscorrelation. More... | |
| template<typename InputIterator1 , typename InputIterator2 , typename OutputIterator > | |
| void | complex_fft_crosscorrelation (InputIterator1 first, InputIterator1 last, InputIterator2 first2, InputIterator2 last2, OutputIterator result_first, OutputIterator result_last) |
| Computes the standard complex crosscorrelation between two sequences using fft. More... | |
| template<typename InputIterator2d1 , typename InputIterator2d2 , typename OutputIterator2d > | |
| void | fft_circular_crosscorrelation2d (InputIterator2d1 in1_upper_left, InputIterator2d1 in1_bottom_right, InputIterator2d2 in2_upper_left, InputIterator2d2 in2_bottom_right, OutputIterator2d out_upper_left, OutputIterator2d out_bottom_right) |
| Computes the circular crosscorrelation between two 2D sequences using fft2d. More... | |
| template<typename InputIterator2d1 , typename InputIterator2d2 , typename OutputIterator2d > | |
| void | fft_crosscorrelation2d (InputIterator2d1 in1_upper_left, InputIterator2d1 in1_bottom_right, InputIterator2d2 in2_upper_left, InputIterator2d2 in2_bottom_right, OutputIterator2d out_upper_left, OutputIterator2d out_bottom_right) |
| Computes the standard crosscorrelation between two 2D sequences using fft2d. More... | |
| template<typename InputIterator2d1 , typename InputIterator2d2 , typename OutputIterator2d > | |
| void | fft_crosscorrelation2d_same (InputIterator2d1 in1_upper_left, InputIterator2d1 in1_bottom_right, InputIterator2d2 in2_upper_left, InputIterator2d2 in2_bottom_right, OutputIterator2d out_upper_left, OutputIterator2d out_bottom_right) |
| Computes the standard crosscorrelation between two 2D sequences using fft2d. More... | |
| template<typename InputIterator3d1 , typename InputIterator3d2 , typename OutputIterator3d > | |
| void | fft_circular_crosscorrelation3d (InputIterator3d1 in1_front_upper_left, InputIterator3d1 in1_back_bottom_right, InputIterator3d2 in2_front_upper_left, InputIterator3d2 in2_back_bottom_right, OutputIterator3d out_front_upper_left, OutputIterator3d out_back_bottom_right) |
| Computes the standard crosscorrelation between two 3D sequences using fft3d. More... | |
| template<typename InputIterator3d1 , typename InputIterator3d2 , typename OutputIterator3d > | |
| void | fft_crosscorrelation3d (InputIterator3d1 in1_front_upper_left, InputIterator3d1 in1_back_bottom_right, InputIterator3d2 in2_front_upper_left, InputIterator3d2 in2_back_bottom_right, OutputIterator3d out_front_upper_left, OutputIterator3d out_back_bottom_right) |
| Computes the standard crosscorrelation between two 3D sequences using fft3d. More... | |
| template<typename InputIterator3d1 , typename InputIterator3d2 , typename OutputIterator3d > | |
| void | fft_crosscorrelation3d_same (InputIterator3d1 in1_front_upper_left, InputIterator3d1 in1_back_bottom_right, InputIterator3d2 in2_front_upper_left, InputIterator3d2 in2_back_bottom_right, OutputIterator3d out_front_upper_left, OutputIterator3d out_back_bottom_right) |
| Computes the standard crosscorrelation between two 3D sequences using fft3d. More... | |
Differential operator algorithms | |
| template<typename RandomAccessIteratorNd1 , typename RandomAccessIteratorNd2 , typename Operator > | |
| void | differential_operator (RandomAccessIteratorNd1 in_first, RandomAccessIteratorNd1 in_last, RandomAccessIteratorNd2 out_first, Operator &op) |
| Applies a differential operator on a range. More... | |
| template<typename RandomAccessIteratorNd1 , typename RandomAccessIteratorNd2 , typename RandomAccessIteratorNd3 , typename Operator1 , typename Operator2 > | |
| void | differential_operator_2 (RandomAccessIteratorNd1 in_first, RandomAccessIteratorNd1 in_last, RandomAccessIteratorNd2 out_first1, RandomAccessIteratorNd3 out_first2, Operator1 &op1, Operator2 &op2) |
| Applies 2 differential operators on a range. More... | |
| template<typename RandomAccessIteratorNd1 , typename RandomAccessIteratorNd2 , typename RandomAccessIteratorNd3 , typename RandomAccessIteratorNd4 , typename Operator1 , typename Operator2 , typename Operator3 > | |
| void | differential_operator_3 (RandomAccessIteratorNd1 in_first, RandomAccessIteratorNd1 in_last, RandomAccessIteratorNd2 out_first1, RandomAccessIteratorNd3 out_first2, RandomAccessIteratorNd4 out_first3, Operator1 &op1, Operator2 &op2, Operator3 &op3) |
| Applies 3 differential operators on a range. More... | |
FFT Tools Functions | |
| unsigned int | bitReverse (unsigned int x, const int log2n) |
| bitReverse function used in the Cooley-Tukey FFT algorithm More... | |
| unsigned int | log2 (unsigned int x) |
| Calculates the log2 of an integer. More... | |
| template<class ForwardIterator > | |
| void | fftshift (ForwardIterator first, ForwardIterator last) |
| Performs a shift of a container, for use with the fft and ifft functions, in order to move the frequency 0 to the center of the container. More... | |
| template<class ForwardIterator2D > | |
| void | fftshift2d (ForwardIterator2D upper_left, ForwardIterator2D bottom_right) |
| Performs a shift of a 2d container, for use with the fft2d and ifft2d functions, in order to move the frequency 0 to the center of the container. More... | |
| template<class ForwardIterator3D > | |
| void | fftshift3d (ForwardIterator3D front_upper_left, ForwardIterator3D back_bottom_right) |
| Performs a shift of a 2d container, for use with the fft2d and ifft2d functions, in order to move the frequency 0 to the center of the container. More... | |
| template<class ForwardIterator4D > | |
| void | fftshift4d (ForwardIterator4D first_front_upper_left, ForwardIterator4D last_back_bottom_right) |
| Performs a shift of a 4d container, for use with the fft4d and ifft4d functions, in order to move the frequency 0 to the center of the container. More... | |
FFT Radix2 (Cooley-Tukey) algorithms. | |
| template<class InputIter_T , class Iter_T > | |
| void | radix2_fft (InputIter_T a, Iter_T b, const int log2n) |
| Computes the Cooley-Tukey (radix2) fft of a container. More... | |
| template<class InputIter_T , class Iter_T > | |
| void | radix2_ifft (InputIter_T a, Iter_T b, const int log2n) |
| Computes the inverse Cooley-Tukey (radix2) fft of a container. More... | |
| template<class InputIter_T , class Iter_T > | |
| void | real_radix2_fft (InputIter_T a, Iter_T b, const int log2n) |
| Computes the Cooley-Tukey (radix2) real_fft of a container. More... | |
| template<typename InputIterator1d , typename OuputIterator1d > | |
| void | radix2_fft1d2d (InputIterator1d begin1, OuputIterator1d begin2, std::size_t nb_lig, std::size_t nb_col) |
| Computes the radix 2 fft2d of a container with 1d iterator (compatible with simple pointers). More... | |
| template<typename InputIterator1d , typename OuputIterator1d > | |
| void | radix2_ifft1d2d (InputIterator1d begin1, OuputIterator1d begin2, std::size_t nb_lig, std::size_t nb_col) |
| Computes the inverse radix 2 fft2d of a container with 1d iterators (compatible with simple pointers). More... | |
| template<typename InputBidirectionalIterator2d , typename OutputBidirectionalIterator2d > | |
| void | radix2_fft2d (InputBidirectionalIterator2d in_upper_left, InputBidirectionalIterator2d in_bottom_right, OutputBidirectionalIterator2d out_upper_left) |
| Computes the radix2 (Cooley-Tukey) fft2d of a container with 2d iterators. More... | |
| template<typename InputBidirectionalIterator2d , typename OutputBidirectionalIterator2d > | |
| void | radix2_ifft2d (InputBidirectionalIterator2d in_upper_left, InputBidirectionalIterator2d in_bottom_right, OutputBidirectionalIterator2d out_upper_left) |
| Computes the radix2 ifft2d of a container with 2d iterators. More... | |
| template<typename Matrix1 , typename Matrix2 > | |
| void | radix2_fft2d (Matrix1 &datain, Matrix2 &dataout) |
| Computes the radix2 fft2d of a container. More... | |
| template<typename Matrix1 , typename Matrix2 > | |
| void | radix2_ifft2d (Matrix1 &datain, Matrix2 &dataout) |
| Computes the radix2 fft2d of a container. More... | |
FFT Split-Radix algorithms (from FFTPACK.hpp). | |
| template<class InputIter , class OutputIter > | |
| void | real_split_radix_fft (InputIter in_begin, InputIter in_end, OutputIter out_begin) |
| Computes the real split radix fft of a container (from FFTPACK.hpp). More... | |
| template<class InputIter , class OutputIter > | |
| void | complex_split_radix_fft (InputIter in_begin, InputIter in_end, OutputIter out_begin) |
| Computes the complex split radix fft of a container (from FFTPACK.hpp). More... | |
| template<class InputIter , class OutputIter > | |
| void | split_radix_ifft (InputIter in_begin, InputIter in_end, OutputIter out_begin) |
| Computes the split radix fft backward of a container (from FFTPACK.hpp). More... | |
| template<typename InputBidirectionalIterator2d , typename OutputBidirectionalIterator2d > | |
| void | real_split_radix_fft2d (InputBidirectionalIterator2d in_upper_left, InputBidirectionalIterator2d in_bottom_right, OutputBidirectionalIterator2d out_upper_left) |
| Computes the real split-radix fft2d of a container with 2d iterators. More... | |
| template<typename InputBidirectionalIterator2d , typename OutputBidirectionalIterator2d > | |
| void | complex_split_radix_fft2d (InputBidirectionalIterator2d in_upper_left, InputBidirectionalIterator2d in_bottom_right, OutputBidirectionalIterator2d out_upper_left) |
| Computes the complex split-radix fft2d of a container with 2d iterators. More... | |
| template<typename InputBidirectionalIterator2d , typename OutputBidirectionalIterator2d > | |
| void | split_radix_ifft2d (InputBidirectionalIterator2d in_upper_left, InputBidirectionalIterator2d in_bottom_right, OutputBidirectionalIterator2d out_upper_left) |
| Computes the split-radix ifft2d of a container with 2d iterators. More... | |
| template<typename InputMatrix , typename OutputMatrix > | |
| void | real_split_radix_fft2d (InputMatrix &datain, OutputMatrix &dataout) |
| Computes the real split-radix fft2d of a container. More... | |
| template<typename InputMatrix , typename OutputMatrix > | |
| void | split_radix_ifft2d (InputMatrix &datain, OutputMatrix &dataout) |
| Computes the split-radix ifft2d of a container. More... | |
| template<typename InputBidirectionalIterator3d , typename OutputBidirectionalIterator3d > | |
| void | real_split_radix_fft3d (InputBidirectionalIterator3d in_front_upper_left, InputBidirectionalIterator3d in_back_bottom_right, OutputBidirectionalIterator3d out_front_upper_left) |
| Computes the real split-radix fft3d of a container with 3d iterators. More... | |
| template<typename InputBidirectionalIterator3d , typename OutputBidirectionalIterator3d > | |
| void | split_radix_ifft3d (InputBidirectionalIterator3d in_front_upper_left, InputBidirectionalIterator3d in_back_bottom_right, OutputBidirectionalIterator3d out_front_upper_left) |
| Computes the split-radix ifft3d of a container with 3d iterators. More... | |
| template<typename InputBidirectionalIterator3d , typename OutputBidirectionalIterator3d > | |
| void | complex_split_radix_fft3d (InputBidirectionalIterator3d in_front_upper_left, InputBidirectionalIterator3d in_back_bottom_right, OutputBidirectionalIterator3d out_front_upper_left) |
| Computes the complex split-radix fft3d of a container with 3d iterators. More... | |
| template<typename InputMatrix3d , typename OutputMatrix3d > | |
| void | complex_split_radix_fft3d (InputMatrix3d &datain, OutputMatrix3d &dataout) |
| Computes the complex split-radix fft3d of a container 3d. More... | |
| template<typename InputMatrix3d , typename OutputMatrix3d > | |
| void | real_split_radix_fft3d (InputMatrix3d &datain, OutputMatrix3d &dataout) |
| Computes the real split-radix fft3d of a container 3d. More... | |
| template<typename InputMatrix3d , typename OutputMatrix3d > | |
| void | split_radix_ifft3d (InputMatrix3d &datain, OutputMatrix3d &dataout) |
| Computes the split-radix ifft3d of a container 3d. More... | |
| template<class InputIter , class OutputIter > | |
| void | split_radix_idct (InputIter in_begin, InputIter in_end, OutputIter out_begin) |
| Computes the split radix Discrete Cosinus Transform III (i.e. idct) of a container (from FFTPACK.hpp). More... | |
| template<class InputIter , class OutputIter > | |
| void | split_radix_dct (InputIter in_begin, InputIter in_end, OutputIter out_begin) |
| Computes the split radix Discrete Cosinus Transform II of a container (from FFTPACK.hpp). More... | |
| template<typename InputBidirectionalIterator4d , typename OutputBidirectionalIterator4d > | |
| void | real_split_radix_fft4d (InputBidirectionalIterator4d in_first_front_upper_left, InputBidirectionalIterator4d in_last_back_bottom_right, OutputBidirectionalIterator4d out_first_front_upper_left) |
| Computes the real split-radix fft4d of a container with 4d iterators. More... | |
| template<typename InputBidirectionalIterator4d , typename OutputBidirectionalIterator4d > | |
| void | complex_split_radix_fft4d (InputBidirectionalIterator4d in_first_front_upper_left, InputBidirectionalIterator4d in_last_back_bottom_right, OutputBidirectionalIterator4d out_first_front_upper_left) |
| Computes the complex split-radix fft4d of a container with 4d iterators. More... | |
| template<typename InputBidirectionalIterator4d , typename OutputBidirectionalIterator4d > | |
| void | split_radix_ifft4d (InputBidirectionalIterator4d in_first_front_upper_left, InputBidirectionalIterator4d in_last_back_bottom_right, OutputBidirectionalIterator4d out_first_front_upper_left) |
| Computes the split-radix ifft4d of a container with 4d iterators. More... | |
| template<typename InputMatrix4d , typename OutputMatrix4d > | |
| void | real_split_radix_fft4d (const InputMatrix4d &datain, OutputMatrix4d &dataout) |
| Computes the real split-radix fft4d of a container 4d. More... | |
| template<typename InputMatrix4d , typename OutputMatrix4d > | |
| void | complex_split_radix_fft4d (const InputMatrix4d &datain, OutputMatrix4d &dataout) |
| Computes the complex split-radix fft4d of a container 4d. More... | |
| template<typename InputMatrix4d , typename OutputMatrix4d > | |
| void | split_radix_ifft4d (const InputMatrix4d &datain, OutputMatrix4d &dataout) |
| Computes the split-radix ifft4d of a container 4d. More... | |
fftw algorithms (from fftw3.h). | |
| template<class ForwardIterator1 , class ForwardIterator2 > | |
| void | fftduplicate (ForwardIterator1 begin1, ForwardIterator2 begin2, ForwardIterator2 end2) |
| Calculates the conjugates of the begin std::complex elements of a first container. Writes them at the end of a second container. This function is used to calculate the negative frequencies after a real fftw. More... | |
| template<class ForwardIterator2D > | |
| void | fftduplicate2d (ForwardIterator2D upper_left, ForwardIterator2D bottom_right) |
| Performs a duplicate of a 2D container, for use with the fft2d and ifft2d functions, in order to calculate the negative frequencies with the real fftw2d. More... | |
| template<class InputIter , class OutputIter > | |
| void | real_fftw (InputIter in_begin, InputIter in_end, OutputIter out_begin) |
| Computes the real fftw of a container (from fftw3.h). More... | |
| template<class InputIter , class OutputIter > | |
| void | complex_fftw (InputIter in_begin, InputIter in_end, OutputIter out_begin) |
| complex fftw of a container (from fftw3.h). More... | |
| template<class InputIter , class OutputIter > | |
| void | ifftw (InputIter in_begin, InputIter in_end, OutputIter out_begin) |
| Computes the fftw backward of a container (from fftw3.h). More... | |
| template<typename InputBidirectionalIterator2d , typename OutputBidirectionalIterator2d > | |
| void | real_fftw2d (InputBidirectionalIterator2d in_upper_left, InputBidirectionalIterator2d in_bottom_right, OutputBidirectionalIterator2d out_upper_left) |
| Computes the real fftw2d of a container with 2d iterators. More... | |
| template<typename InputBidirectionalIterator2d , typename OutputBidirectionalIterator2d > | |
| void | complex_fftw2d (InputBidirectionalIterator2d in_upper_left, InputBidirectionalIterator2d in_bottom_right, OutputBidirectionalIterator2d out_upper_left) |
| Computes the complex fftw2d of a container with 2d iterators. More... | |
| template<typename InputBidirectionalIterator2d , typename OutputBidirectionalIterator2d > | |
| void | ifftw2d (InputBidirectionalIterator2d in_upper_left, InputBidirectionalIterator2d in_bottom_right, OutputBidirectionalIterator2d out_upper_left) |
| Computes the ifftw2d of a container with 2d iterators. More... | |
| template<typename InputMatrix , typename OutputMatrix > | |
| void | real_fftw2d (InputMatrix &datain, OutputMatrix &dataout) |
| Computes the real fftw2d of a container. More... | |
| template<typename InputMatrix , typename OutputMatrix > | |
| void | ifftw2d (InputMatrix &datain, OutputMatrix &dataout) |
| Computes the ifftw2d of a container. More... | |
| template<typename InputBidirectionalIterator3d , typename OutputBidirectionalIterator3d > | |
| void | real_fftw3d (InputBidirectionalIterator3d in_front_upper_left, InputBidirectionalIterator3d in_back_bottom_right, OutputBidirectionalIterator3d out_front_upper_left) |
| Computes the real fftw3d of a container with 3d iterators. More... | |
| template<typename InputBidirectionalIterator3d , typename OutputBidirectionalIterator3d > | |
| void | complex_fftw3d (InputBidirectionalIterator3d in_front_upper_left, InputBidirectionalIterator3d in_back_bottom_right, OutputBidirectionalIterator3d out_front_upper_left) |
| Computes the complex fftw3d of a container with 3d iterators. More... | |
| template<typename InputBidirectionalIterator3d , typename OutputBidirectionalIterator3d > | |
| void | complex_fft3d (InputBidirectionalIterator3d in_front_upper_left, InputBidirectionalIterator3d in_back_bottom_right, OutputBidirectionalIterator3d out_front_upper_left) |
| Computes the complex fft3d of a container with 3d iterators. More... | |
| template<typename Volume1 , typename Volume2 > | |
| void | complex_fft3d (Volume1 &datain, Volume2 &dataout) |
| Computes the complex fft3d of a container. More... | |
| template<typename InputBidirectionalIterator3d , typename OutputBidirectionalIterator3d > | |
| void | ifftw3d (InputBidirectionalIterator3d in_front_upper_left, InputBidirectionalIterator3d in_back_bottom_right, OutputBidirectionalIterator3d out_front_upper_left) |
| Computes the ifftw3d of a container with 3d iterators. More... | |
| template<typename InputMatrix3d , typename OutputMatrix3d > | |
| void | real_fftw3d (InputMatrix3d &datain, OutputMatrix3d &dataout) |
| Computes the real fftw3d of a container 3d. More... | |
| template<typename InputMatrix3d , typename OutputMatrix3d > | |
| void | complex_fftw3d (InputMatrix3d &datain, OutputMatrix3d &dataout) |
| Computes the complex fftw3d of a container 3d. More... | |
| template<typename InputMatrix3d , typename OutputMatrix3d > | |
| void | ifftw3d (InputMatrix3d &datain, OutputMatrix3d &dataout) |
| Computes the ifftw3d of a container 3d. More... | |
| template<class InputIter , class OutputIter > | |
| void | fftw_dct (InputIter in_begin, InputIter in_end, OutputIter out_begin) |
| Computes the Discrete Cosinus Transform II (forward) of a container (from fftw). More... | |
| template<class InputIter , class OutputIter > | |
| void | fftw_idct (InputIter in_begin, InputIter in_end, OutputIter out_begin) |
| Computes the Discrete Cosinus Transform III (backward) of a container (from fftw). More... | |
| template<typename InputBidirectionalIterator4d , typename OutputBidirectionalIterator4d > | |
| void | real_fftw4d (InputBidirectionalIterator4d in_first_front_upper_left, InputBidirectionalIterator4d in_last_back_bottom_right, OutputBidirectionalIterator4d out_first_front_upper_left) |
| Computes the real fftw4d of a container with 4d iterators. More... | |
| template<typename InputBidirectionalIterator4d , typename OutputBidirectionalIterator4d > | |
| void | complex_fftw4d (InputBidirectionalIterator4d in_first_front_upper_left, InputBidirectionalIterator4d in_last_back_bottom_right, OutputBidirectionalIterator4d out_first_front_upper_left) |
| Computes the complex fftw4d of a container with 4d iterators. More... | |
| template<typename InputBidirectionalIterator4d , typename OutputBidirectionalIterator4d > | |
| void | ifftw4d (InputBidirectionalIterator4d in_first_front_upper_left, InputBidirectionalIterator4d in_last_back_bottom_right, OutputBidirectionalIterator4d out_first_front_upper_left) |
| Computes the ifftw4d of a container with 4d iterators. More... | |
| template<typename InputMatrix4d , typename OutputMatrix4d > | |
| void | real_fftw4d (const InputMatrix4d &datain, OutputMatrix4d &dataout) |
| Computes the real fftw4d of a container 4d. More... | |
| template<typename InputMatrix4d , typename OutputMatrix4d > | |
| void | complex_fftw4d (const InputMatrix4d &datain, OutputMatrix4d &dataout) |
| Computes the complex fftw4d of a container 4d. More... | |
| template<typename InputMatrix4d , typename OutputMatrix4d > | |
| void | ifftw4d (const InputMatrix4d &datain, OutputMatrix4d &dataout) |
| Computes the ifftw4d of a container 4d. More... | |
FFT Generic Algorithms | |
| template<class InputIter , class OutputIter > | |
| void | real_fft (InputIter in_begin, InputIter in_end, OutputIter out_begin) |
| Computes the real fft of a container. More... | |
| template<class InputIter , class OutputIter > | |
| void | complex_fft (InputIter in_begin, InputIter in_end, OutputIter out_begin) |
| Computes the complex fft of a container. More... | |
| template<class InputIter , class OutputIter > | |
| void | ifft (InputIter in_begin, InputIter in_end, OutputIter out_begin) |
| Computes the inverse fft of a container. More... | |
| template<typename InputBidirectionalIterator2d , typename OutputBidirectionalIterator2d > | |
| void | real_fft2d (InputBidirectionalIterator2d in_upper_left, InputBidirectionalIterator2d in_bottom_right, OutputBidirectionalIterator2d out_upper_left) |
| Computes the real fft2d of a container with 2d iterators. More... | |
| template<typename InputBidirectionalIterator2d , typename OutputBidirectionalIterator2d > | |
| void | complex_fft2d (InputBidirectionalIterator2d in_upper_left, InputBidirectionalIterator2d in_bottom_right, OutputBidirectionalIterator2d out_upper_left) |
| Computes the complex fft2d of a container with 2d iterators. More... | |
| template<typename InputBidirectionalIterator2d , typename OutputBidirectionalIterator2d > | |
| void | ifft2d (InputBidirectionalIterator2d in_upper_left, InputBidirectionalIterator2d in_bottom_right, OutputBidirectionalIterator2d out_upper_left) |
| Computes the ifft2d of a container with 2d iterators. More... | |
| template<typename Matrix1 , typename Matrix2 > | |
| void | real_fft2d (Matrix1 &datain, Matrix2 &dataout) |
| Computes the real fft2d of a container. More... | |
| template<typename Matrix1 , typename Matrix2 > | |
| void | complex_fft2d (Matrix1 &datain, Matrix2 &dataout) |
| Computes the complex fft2d of a container. More... | |
| template<typename Matrix1 , typename Matrix2 > | |
| void | ifft2d (Matrix1 &datain, Matrix2 &dataout) |
| Computes the fft2d of a container. More... | |
| template<typename InputBidirectionalIterator3d , typename OutputBidirectionalIterator3d > | |
| void | real_fft3d (InputBidirectionalIterator3d in_front_upper_left, InputBidirectionalIterator3d in_back_bottom_right, OutputBidirectionalIterator3d out_front_upper_left) |
| Computes the real fft3d of a container with 3d iterators. More... | |
| template<typename InputBidirectionalIterator3d , typename OutputBidirectionalIterator3d > | |
| void | ifft3d (InputBidirectionalIterator3d in_front_upper_left, InputBidirectionalIterator3d in_back_bottom_right, OutputBidirectionalIterator3d out_front_upper_left) |
| Computes the ifft3d of a container with 3d iterators. More... | |
| template<typename Volume1 , typename Volume2 > | |
| void | real_fft3d (Volume1 &datain, Volume2 &dataout) |
| Computes the real fft3d of a container. More... | |
| template<typename Volume1 , typename Volume2 > | |
| void | ifft3d (Volume1 &datain, Volume2 &dataout) |
| Computes the fft3d of a container. More... | |
| template<class InputIter , class OutputIter > | |
| void | dct (InputIter in_begin, InputIter in_end, OutputIter out_begin) |
| Computes the Discrete Cosinus Transform II (forward) of a container. More... | |
| template<class InputIter , class OutputIter > | |
| void | idct (InputIter in_begin, InputIter in_end, OutputIter out_begin) |
| Computes the Discrete Cosinus Transform III (backward) of a container. More... | |
| template<typename InputBidirectionalIterator4d , typename OutputBidirectionalIterator4d > | |
| void | real_fft4d (InputBidirectionalIterator4d in_first_front_upper_left, InputBidirectionalIterator4d in_last_back_bottom_right, OutputBidirectionalIterator4d out_first_front_upper_left) |
| Computes the real fft4d of a container with 4d iterators. More... | |
| template<typename InputBidirectionalIterator4d , typename OutputBidirectionalIterator4d > | |
| void | complex_fft4d (InputBidirectionalIterator4d in_first_front_upper_left, InputBidirectionalIterator4d in_last_back_bottom_right, OutputBidirectionalIterator4d out_first_front_upper_left) |
| Computes the complex fft4d of a container with 4d iterators. More... | |
| template<typename InputBidirectionalIterator4d , typename OutputBidirectionalIterator4d > | |
| void | ifft4d (InputBidirectionalIterator4d in_first_front_upper_left, InputBidirectionalIterator4d in_last_back_bottom_right, OutputBidirectionalIterator4d out_first_front_upper_left) |
| Computes the ifft4d of a container with 4d iterators. More... | |
| template<typename HyperVolume1 , typename HyperVolume2 > | |
| void | real_fft4d (const HyperVolume1 &datain, HyperVolume2 &dataout) |
| Computes the real fft4d of a container. More... | |
| template<typename HyperVolume1 , typename HyperVolume2 > | |
| void | complex_fft4d (const HyperVolume1 &datain, HyperVolume2 &dataout) |
| Computes the complex fft4d of a container. More... | |
| template<typename HyperVolume1 , typename HyperVolume2 > | |
| void | ifft4d (const HyperVolume1 &datain, HyperVolume2 &dataout) |
| Computes the fft4d of a container. More... | |
Miscellaneous algorithms | |
| std::size_t | split_extension (const std::string &file_path_name, std::string &file_path_name_cut, std::string &ext) |
| Split a file_name in two substrings: the file_path_name string without the extension and the extension string. More... | |
| std::string | compose_file_name (const std::string &file_path_name, const std::size_t img) |
| Compose a file_name from the file name format basenamend*.ext. More... | |
| template<typename Container > | |
| void | print (const Container &C, const std::string &name="") |
| Print the name of the container follow by the values of the container in a terminal. More... | |
Raw input/output algorithms | |
| template<typename InputIterator > | |
| void | write_raw (InputIterator first, InputIterator last, const std::string &file_path_name) |
| Write a Container to an raw file. More... | |
| template<typename InputIterator > | |
| void | read_raw (const std::string &file_path_name, InputIterator first, InputIterator last) |
| Write a Container to an raw file. More... | |
2d containers input/output | |
| template<typename RandomAccessIterator2d , typename WriteType > | |
| void | write_ascii_2d (RandomAccessIterator2d upper_left, RandomAccessIterator2d bottom_right, const std::string &file_path_name) |
| Write a Container2d to an ASCII file. More... | |
| template<typename Container2d , typename WriteType > | |
| void | write_ascii_2d (const Container2d &cont, const std::string &file_path_name) |
| Write a Container2d to an ASCII file. More... | |
| template<typename Container2d > | |
| void | read_ascii_2d (Container2d &container, const std::string &file_path_name) |
| Read a Container2d from an ASCII file. More... | |
| template<typename RandomAccessIterator2d , typename WriteType > | |
| void | write_tecplot_2d (RandomAccessIterator2d upper_left, RandomAccessIterator2d bottom_right, const std::string &file_path_name, const std::string &title, const std::string &zone, const int precision=6) |
| Write a Container2d to an ASCII file. More... | |
2d vector fields input/output | |
| template<typename MultiContainer2d > | |
| void | write_gnuplot_vect2d (const MultiContainer2d &field, const std::string &file_path_name, const int precision=6) |
| Write a DenseVector2dField2D to a gnuplot file. More... | |
| template<typename MultiContainer2d , typename T > | |
| void | write_gnuplot_vect2d (const MultiContainer2d &field, const slip::Point2d< T > &init_point, const slip::Point2d< T > &step, const std::string &file_path_name, const int precision=6) |
| Write a DenseVector2dField2D to a gnuplot file handle real regular grid 2d. More... | |
| template<typename MultiContainer2d > | |
| void | write_tecplot_vect2d (const MultiContainer2d &field, const std::string &file_path_name, const std::string &title, const std::string &zone, const int precision=6) |
| Write a DenseVector2dField2D to a tecplot file. More... | |
| template<typename MultiContainer2d , typename T > | |
| void | write_tecplot_vect2d (const MultiContainer2d &field, const slip::Point2d< T > &init_point, const slip::Point2d< T > &step, const std::string &file_path_name, const std::string &title, const std::string &zone, const int precision=6) |
| Write a DenseVector2dField2D to a tecplot file handle real regular grid 2d. More... | |
| template<class MultiContainer2d > | |
| void | read_tecplot_vect2d (const std::string &file_path_name, MultiContainer2d &field) |
| Create a DenseVector2dField2D from a tecplot file. More... | |
| template<class MultiContainer2d , typename T > | |
| void | read_tecplot_vect2d (const std::string &file_path_name, MultiContainer2d &field, slip::Point2d< T > &init_point, slip::Point2d< T > &step) |
| Create a DenseVector2dField2D from a tecplot file handle 2d real regular grid. More... | |
| template<typename MultiContainer2d > | |
| void | read_tecplot_XY (const std::string &file_path_name, MultiContainer2d &XY) |
| Create a XY DenseVector2dField2D from a tecplot file. More... | |
| template<typename Vector1 , typename Vector2 > | |
| void | read_tecplot_XY (const std::string &file_path_name, Vector1 &X, Vector2 &Y) |
| Reads X and Y column of an ASCII 2d tecplot file. More... | |
| template<class MultiContainer2d > | |
| void | read_gnuplot_vect2d (const std::string &file_path_name, MultiContainer2d &field) |
| Create a DenseVector2dField2D from a gnuplot file. More... | |
| template<class MultiContainer2d , typename T > | |
| void | read_gnuplot_vect2d (const std::string &file_path_name, MultiContainer2d &field, slip::Point2d< T > &init_point, slip::Point2d< T > &step) |
| Create a DenseVector2dField2D from a gnuplot file handle 2d real regular grid. More... | |
| template<typename MultiContainer2d > | |
| void | read_gnuplot_XY (const std::string &file_path_name, MultiContainer2d &XY) |
| Create a XY DenseVector2dField2D from a gnuplot file. More... | |
| template<typename Vector1 , typename Vector2 > | |
| void | read_gnuplot_XY (const std::string &file_path_name, Vector1 &X, Vector2 &Y) |
| Read X and Y column of a 2d gnuplot ASCII file. More... | |
3d vector fields input/output | |
| template<typename DenseVector3dField3d > | |
| void | write_tecplot_vect3d (const DenseVector3dField3d &field, const std::string &file_path_name, const std::string &title, const std::string &zone, const int precision=6) |
| Write a DenseVector3dField3D to a tecplot file. More... | |
| template<typename DenseVector3dField3d , typename T > | |
| void | write_tecplot_vect3d (const DenseVector3dField3d &field, const slip::Point3d< T > &init_point, const slip::Point3d< T > &step, const std::string &file_path_name, const std::string &title, const std::string &zone, const int precision=6) |
| Write a DenseVector3dField3D to a tecplot file handle 3d real regular grid. More... | |
| template<class MultiContainer3d > | |
| void | read_tecplot_vect3d (const std::string &file_path_name, MultiContainer3d &field) |
| Create a DenseVector3dField3D from a tecplot file. More... | |
| template<class MultiContainer3d , typename T > | |
| void | read_tecplot_vect3d (const std::string &file_path_name, MultiContainer3d &field, slip::Point3d< T > &init_point, slip::Point3d< T > &step) |
| Create a DenseVector3dField3D from a tecplot file handle 3d real regular grid. More... | |
| template<class MultiContainer3d > | |
| void | read_tecplot_XYZ (const std::string &file_path_name, MultiContainer3d &XYZ) |
| Create a XYZ DenseVector3dField3D from a tecplot file. More... | |
| template<class Vector1 , class Vector2 , class Vector3 > | |
| void | read_tecplot_XYZ (const std::string &file_path_name, Vector1 &X, Vector2 &Y, Vector3 &Z) |
| Create a XYZ DenseVector3dField3D from a tecplot file. More... | |
| template<class MultiContainer3d > | |
| void | read_gnuplot_XYZ (const std::string &file_path_name, MultiContainer3d &XYZ) |
| Create a XYZ DenseVector3dField3D from a gnuplot file. More... | |
1d ASCII containers input/output | |
| template<typename InputIterator , typename WriteType > | |
| void | write_ascii_1d (InputIterator first, InputIterator last, const std::string &file_path_name) |
| Write a Container1d to an ASCII file. More... | |
| template<typename Container1d > | |
| void | read_ascii_1d (const std::string &file_path_name, Container1d &container) |
| Read a Container1d from an ASCII file. More... | |
container3d (volume) input/output | |
| template<typename Container3d > | |
| void | write_tecplot_vol (const Container3d &container, const std::string &file_path_name, const std::string &title) |
| Write a Container3D to a tecplot file. More... | |
| template<typename Container3d > | |
| void | write_to_images_tecplot (Container3d &container, const std::string &file_path_name, const std::string &title, const std::size_t from, const std::size_t to) |
| Write slices of a Container3D to a tecplot file. More... | |
Matrix vector algorithms | |
| template<class RandomAccessIterator2d , class RandomAccessIterator1 , class RandomAccessIterator2 > | |
| void | matrix_vector_multiplies (RandomAccessIterator2d M_upper_left, RandomAccessIterator2d M_bottom_right, RandomAccessIterator1 first1, RandomAccessIterator1 last1, RandomAccessIterator2 result_first, RandomAccessIterator2 result_last) |
| Computes the multiplication of a Matrix and a Vector: Result=MV. More... | |
| template<typename AT , typename RandomAccessIterator1 , typename RandomAccessIterator2 > | |
| void | aXpY (const AT &a, RandomAccessIterator1 first1, RandomAccessIterator1 last1, RandomAccessIterator2 first2) |
| Computes the saxpy ("scalar a x plus b") for each element of two ranges x and y. More... | |
| template<typename RandomAccessIterator1 , typename T , typename RandomAccessIterator2 > | |
| void | vector_scalar_multiplies (RandomAccessIterator1 V_first, RandomAccessIterator1 V_last, const T &scal, RandomAccessIterator2 result_first) |
| Computes the multiplication of a vector V by a scalar scal. More... | |
| template<typename Vector1 , typename T , typename Vector2 > | |
| void | vector_scalar_multiplies (const Vector1 &V, const T &scal, Vector2 &Result) |
| Computes the multiplication of a vector V by a scalar scal. More... | |
| template<typename RandomAccessIterator1 , typename T , typename RandomAccessIterator2 > | |
| void | conj_vector_scalar_multiplies (RandomAccessIterator1 V_first, RandomAccessIterator1 V_last, const T &scal, RandomAccessIterator2 result_first) |
Computes the multiplication of a vector 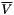 by a scalar scal. More... by a scalar scal. More... | |
| template<typename Vector1 , typename T , typename Vector2 > | |
| void | conj_vector_scalar_multiplies (const Vector1 &V, const T &scal, Vector2 &Result) |
Computes the multiplication of a vector 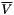 by a scalar scal. More... by a scalar scal. More... | |
| template<class RandomAccessIterator2d1 , class T , class RandomAccessIterator2d2 > | |
| void | matrix_scalar_multiplies (RandomAccessIterator2d1 M_upper_left, RandomAccessIterator2d1 M_bottom_right, const T &scal, RandomAccessIterator2d2 R_upper_left, RandomAccessIterator2d2 R_bottom_right) |
| Computes the multiplication of a Matrix by a scalar R = M*scal. More... | |
| template<class Matrix1 , class T , class Matrix2 > | |
| void | matrix_scalar_multiplies (const Matrix1 &M, const T &scal, Matrix2 &R) |
| Computes the multiplication of a Matrix by a scalar R = M*scal. More... | |
| template<class Matrix , class Vector1 , class Vector2 > | |
| void | matrix_vector_multiplies (const Matrix &M, const Vector1 &V, Vector2 &Result) |
| Computes the multiplication of a Matrix and a Vector: Result=MV. More... | |
| template<class RandomAccessIterator2d , class RandomAccessIterator1 , class RandomAccessIterator2 > | |
| void | hvector_matrix_multiplies (RandomAccessIterator1 V_first, RandomAccessIterator1 V_last, RandomAccessIterator2d M_up, RandomAccessIterator2d M_bot, RandomAccessIterator2 result_first, RandomAccessIterator2 result_last) |
| Computes the hermitian left multiplication:
. More... | |
| template<class Vector1 , class Matrix , class Vector2 > | |
| void | hvector_matrix_multiplies (const Vector1 &V, const Matrix &M, Vector2 &R) |
| Computes the hermitian left multiplication:
. More... | |
| template<class RandomAccessIterator2d , class RandomAccessIterator1 , class RandomAccessIterator2 > | |
| void | tvector_matrix_multiplies (RandomAccessIterator1 V_first, RandomAccessIterator1 V_last, RandomAccessIterator2d M_up, RandomAccessIterator2d M_bot, RandomAccessIterator2 result_first, RandomAccessIterator2 result_last) |
| Computes the transpose left multiplication:
. More... | |
| template<class Vector1 , class Matrix , class Vector2 > | |
| void | tvector_matrix_multiplies (const Vector1 &V, const Matrix &M, Vector2 &R) |
| Computes the transpose left multiplication:
. More... | |
| template<class RandomAccessIterator2d1 , class RandomAccessIterator2d2 , class RandomAccessIterator2d3 > | |
| void | hmatrix_matrix_multiplies (RandomAccessIterator2d1 M1_up, RandomAccessIterator2d1 M1_bot, RandomAccessIterator2d2 M2_up, RandomAccessIterator2d2 M2_bot, RandomAccessIterator2d3 result_up, RandomAccessIterator2d3 result_bot) |
| Computes the hermitian left multiplication of a matrix:
. More... | |
| template<class Matrix1 , class Matrix2 , class Matrix3 > | |
| void | hmatrix_matrix_multiplies (const Matrix1 &M1, const Matrix2 &M2, Matrix3 &Result) |
| Computes the hermitian left multiplication of a matrix:
. More... | |
| template<class RandomAccessIterator2d , class RandomAccessIterator1 , class RandomAccessIterator2 > | |
| void | hmatrix_vector_multiplies (RandomAccessIterator2d M_up, RandomAccessIterator2d M_bot, RandomAccessIterator1 V_first, RandomAccessIterator1 V_last, RandomAccessIterator2 R_first, RandomAccessIterator2 R_last) |
| Computes the hermitian matrix left multiplication of a vector:
. More... | |
| template<class Matrix , class Vector1 , class Vector2 > | |
| void | hmatrix_vector_multiplies (const Matrix &M, const Vector1 &V, Vector2 &R) |
| Computes the hermitian matrix left multiplication of a vector:
. More... | |
| template<typename RandomAccessIterator2d , typename RandomAccessIterator1 , typename RandomAccessIterator2 > | |
| void | gen_matrix_vector_multiplies (RandomAccessIterator2d M_up, RandomAccessIterator2d M_bot, RandomAccessIterator1 V_first, RandomAccessIterator1 V_last, RandomAccessIterator2 Y_first, RandomAccessIterator2 Y_last) |
| Computes the generalised multiplication of a Matrix and a Vector: computes the update
. More... | |
| template<class Matrix , class Vector1 , class Vector2 > | |
| void | gen_matrix_vector_multiplies (const Matrix &M, const Vector1 &V, Vector2 &Y) |
| Computes the generalised multiplication of a Matrix and a Vector: computes the update
. More... | |
| template<typename MatrixIterator1 , typename MatrixIterator2 , typename MatrixIterator3 > | |
| void | matrix_matrix_multiplies (MatrixIterator1 M1_up, MatrixIterator1 M1_bot, MatrixIterator2 M2_up, MatrixIterator2 M2_bot, MatrixIterator3 R_up, MatrixIterator3 R_bot) |
| Computes the matrix matrix multiplication of 2 2d ranges. More... | |
| template<class Matrix1 , class Matrix2 , class Matrix3 > | |
| void | matrix_matrix_multiplies (const Matrix1 &M1, const Matrix2 &M2, Matrix3 &Result) |
| Computes the multiplication of a two Matrix. More... | |
| template<typename RandomAccessIterator2d1 , typename RandomAccessIterator2d2 , typename RandomAccessIterator2d3 > | |
| void | gen_matrix_matrix_multiplies (RandomAccessIterator2d1 A_up, RandomAccessIterator2d1 A_bot, RandomAccessIterator2d2 B_up, RandomAccessIterator2d2 B_bot, RandomAccessIterator2d3 C_up, RandomAccessIterator2d3 C_bot) |
| Computes the generalized multiplication of a two Matrix:
. More... | |
| template<class Matrix1 , class Matrix2 , class Matrix3 > | |
| void | gen_matrix_matrix_multiplies (const Matrix1 &A, const Matrix2 &B, Matrix3 &C) |
| Computes the generalized multiplication of a two Matrix:
. More... | |
| template<class Matrix1 , class Matrix2 , class Matrix3 > | |
| void | multiplies (const Matrix1 &M1, const std::size_t nr1, const std::size_t nc1, const Matrix2 &M2, const std::size_t nr2, const std::size_t nc2, Matrix3 &Result, const std::size_t nr3, const std::size_t nc3) |
| Computes the multiplication of two Matrix. More... | |
| template<class Matrix1 , class Matrix2 , class Matrix3 > | |
| void | multiplies (const Matrix1 &M, const std::size_t nrm, const std::size_t ncm, const Matrix2 &V, const std::size_t nrv, Matrix3 &Result, const std::size_t nrr) |
| Computes the multiplication of a Matrix with a Vector. More... | |
| template<class Matrix1 , class Matrix2 , class Matrix3 > | |
| void | multiplies (const Matrix1 &M1, const Matrix2 &M2, Matrix3 &Result) |
| Computes the multiplication of two Matrix. More... | |
| template<typename MatrixIterator1 , typename MatrixIterator2 , typename MatrixIterator3 > | |
| void | multiplies (MatrixIterator1 A1_up, MatrixIterator1 A1_bot, MatrixIterator2 A2_up, MatrixIterator2 A2_bot, MatrixIterator3 Res_up, MatrixIterator3 Res_bot) |
Computes the multiplication of two matrices 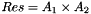 . More... . More... | |
| template<class RandomAccessIterator2d1 , class RandomAccessIterator2d2 > | |
| void | matrix_matrixt_multiplies (RandomAccessIterator2d1 M1_up, RandomAccessIterator2d1 M1_bot, RandomAccessIterator2d2 Res_up, RandomAccessIterator2d2 Res_bot) |
Computes the multiplication of a matrix with its transposate A^T 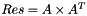 . More... . More... | |
| template<class Matrix1 , class Matrix2 > | |
| void | matrix_matrixt_multiplies (const Matrix1 &M1, Matrix2 &result) |
Computes the multiplication of A and its transposate AT 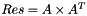 . More... . More... | |
| template<class RandomAccessIterator2d1 , class T , class RandomAccessIterator2d2 > | |
| void | matrix_shift (RandomAccessIterator2d1 M_upper_left, RandomAccessIterator2d1 M_bottom_right, const T &lambda, RandomAccessIterator2d2 R_upper_left, RandomAccessIterator2d2 R_bottom_right) |
| Computes
with In the identity matrix. More... | |
| template<class RandomAccessIterator2d1 , class T > | |
| void | matrix_shift (RandomAccessIterator2d1 M_upper_left, RandomAccessIterator2d1 M_bottom_right, const T &lambda) |
| Computes
with In the identity matrix. More... | |
| template<class Matrix1 , class T , class Matrix2 > | |
| void | matrix_shift (const Matrix1 &A, const T &lambda, Matrix2 &R) |
| Computes
with In the identity matrix. More... | |
| template<class Matrix , class T > | |
| void | matrix_shift (Matrix &A, const T &lambda) |
| Computes
with In the identity matrix. More... | |
| template<typename RandomAccessIterator2d1 , typename T , typename RandomAccessIterator1 , typename RandomAccessIterator2 > | |
| void | rank1_update (RandomAccessIterator2d1 A_up, RandomAccessIterator2d1 A_bot, const T &alpha, RandomAccessIterator1 X_first, RandomAccessIterator1 X_last, RandomAccessIterator2 Y_first, RandomAccessIterator2 Y_last) |
| Computes
. More... | |
| template<typename Matrix , typename T , typename Vector1 , typename Vector2 > | |
| void | rank1_update (Matrix &A, const T &alpha, const Vector1 &X, const Vector2 &Y) |
| Computes
. More... | |
| template<typename Iterator1 , typename Iterator2 , typename U > | |
| void | reduction (Iterator1 seq1_beg, Iterator1 seq1_end, Iterator2 seq2_beg, U u) |
| Add u times the second sequence to the first one: seq1 = seq1 + u * seq2. More... | |
| template<class Matrix1 , class Matrix2 > | |
| void | hermitian_transpose (const Matrix1 &M, Matrix2 &TM) |
Computes the hermitian transpose of a matrix 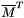 which is the transpose of the conjugate. More... which is the transpose of the conjugate. More... | |
| template<class Matrix1 , class Matrix2 > | |
| void | transpose (const Matrix1 &M, const std::size_t nr1, const std::size_t nc1, Matrix2 &TM, const std::size_t nr2, const std::size_t nc2) |
Computes the transpose of a matrix 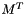 . More... . More... | |
| template<class Matrix1 , class Matrix2 > | |
| void | transpose (const Matrix1 &M, Matrix2 &TM) |
Computes the transpose of a matrix 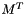 . More... . More... | |
| template<class Matrix1 , class Matrix2 > | |
| void | conj (const Matrix1 &M, Matrix2 &CM) |
Computes the conjugate of a matrix 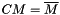 . More... . More... | |
| template<class Matrix1 , class Matrix2 > | |
| void | real (const Matrix1 &C, Matrix2 &R) |
Extract the real Matrix of a complex Matrix. 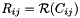 . More... . More... | |
| template<class Matrix1 , class Matrix2 > | |
| void | imag (const Matrix1 &C, Matrix2 &I) |
Extract the imaginary Matrix of a complex Matrix. 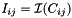 . More... . More... | |
| template<typename VectorIterator1 , typename VectorIterator2 , typename MatrixIterator > | |
| void | outer_product (VectorIterator1 V_begin, VectorIterator1 V_end, VectorIterator2 W_begin, VectorIterator2 W_end, MatrixIterator R_up, MatrixIterator R_bot) |
| Computes the hermitian outer product of the vector V and the transpose of the conjugate of the vector W:
. More... | |
| template<class RandomAccessIterator1 , class RandomAccessIterator2 , class RandomAccessIterator2d > | |
| void | rank1_tensorial_product (RandomAccessIterator1 base1_first, RandomAccessIterator1 base1_end, RandomAccessIterator2 base2_first, RandomAccessIterator2 base2_end, RandomAccessIterator2d matrix_upper_left, RandomAccessIterator2d matrix_bottom_right) |
Computes the tensorial product of two rank one tensors 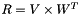 it provides a rank2 tensor (Container2d) of size (MxN) if M and N are respectivly the size of V and W. More... it provides a rank2 tensor (Container2d) of size (MxN) if M and N are respectivly the size of V and W. More... | |
| template<class RandomAccessIterator1 , class RandomAccessIterator2 , class RandomAccessIterator3 , class RandomAccessIterator3d > | |
| void | rank1_tensorial_product (RandomAccessIterator1 base1_first, RandomAccessIterator1 base1_end, RandomAccessIterator2 base2_first, RandomAccessIterator2 base2_end, RandomAccessIterator3 base3_first, RandomAccessIterator3 base3_end, RandomAccessIterator3d base_front_upper_left, RandomAccessIterator3d base_back_bottom_right) |
| Computes the tensorial product of three rank one tensors it provides a rank3 tensor (Container3d) of size (PxMxN) if P, M and N are respectivly the size of V, W and X. More... | |
Inner-poduct algorithms | |
| template<typename RandomAccessIterator1 , typename RandomAccessIterator2 > | |
| std::iterator_traits < RandomAccessIterator1 > ::value_type | hermitian_inner_product (RandomAccessIterator1 first1, RandomAccessIterator1 last1, RandomAccessIterator2 first2, typename std::iterator_traits< RandomAccessIterator1 >::value_type init) |
| Computes the hermitian inner-product of two ranges X and Y:
. More... | |
| template<typename RandomAccessIterator1 , typename RandomAccessIterator2 > | |
| std::iterator_traits < RandomAccessIterator1 > ::value_type | inner_product (RandomAccessIterator1 first1, RandomAccessIterator1 last1, RandomAccessIterator2 first2, typename std::iterator_traits< RandomAccessIterator1 >::value_type init=typename std::iterator_traits< RandomAccessIterator1 >::value_type()) |
| Computes the inner_product of two ranges X and Y:
. More... | |
| template<typename Vector1 , typename Vector2 > | |
| Vector1::value_type | inner_product (const Vector1 &V1, const Vector2 &V2) |
| Computes the inner_product of two ranges X and Y:
. More... | |
| template<typename RandomAccessIterator1 , typename RandomAccessIterator2d , typename RandomAccessIterator2 > | |
| std::iterator_traits < RandomAccessIterator2 > ::value_type | gen_inner_product (RandomAccessIterator1 first1, RandomAccessIterator1 last1, RandomAccessIterator2d A_upper_left, RandomAccessIterator2d A_bottom_right, RandomAccessIterator2 first2, RandomAccessIterator2 last2, typename std::iterator_traits< RandomAccessIterator2 >::value_type init=typename std::iterator_traits< RandomAccessIterator2 >::value_type()) |
| Computes the generalized inner_product of two ranges:
. More... | |
| template<typename Vector1 , typename Matrix , typename Vector2 > | |
| Vector2::value_type | gen_inner_product (const Vector1 &X, const Matrix &M, const Vector2 &Y) |
| Computes the generalized inner_product of two ranges:
. More... | |
| template<typename RandomAccessIterator1 , typename RandomAccessIterator2d > | |
| std::iterator_traits < RandomAccessIterator1 > ::value_type | rayleigh (RandomAccessIterator1 first1, RandomAccessIterator1 last1, RandomAccessIterator2d A_upper_left, RandomAccessIterator2d A_bottom_right) |
| Computes the rayleigh coefficient of a vector x:
. More... | |
| template<typename Vector , typename Matrix > | |
| Vector::value_type | rayleigh (const Vector &X, const Matrix &A) |
| Computes the rayleigh coefficient o f a vector x:
. More... | |
Marix norms | |
| template<typename InputIterator > | |
| slip::lin_alg_traits< typename std::iterator_traits < InputIterator >::value_type > ::value_type | L22_norm_cplx (InputIterator first, InputIterator last) |
Computes the L22 norm 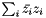 of a complex container. More... of a complex container. More... | |
| template<typename RandomAccessIterator2d > | |
| slip::lin_alg_traits< typename std::iterator_traits < RandomAccessIterator2d > ::value_type >::value_type | row_norm (RandomAccessIterator2d upper_left, RandomAccessIterator2d bottom_right) |
Computes the row norm ( 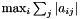 ) of a 2d range. More... ) of a 2d range. More... | |
| template<typename Container2d > | |
| slip::lin_alg_traits< typename Container2d::value_type > ::value_type | row_norm (const Container2d &container) |
Computes the row norm ( 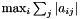 ) of a Container2d. More... ) of a Container2d. More... | |
| template<typename RandomAccessIterator2d > | |
| slip::lin_alg_traits< typename std::iterator_traits < RandomAccessIterator2d > ::value_type >::value_type | col_norm (RandomAccessIterator2d upper_left, RandomAccessIterator2d bottom_right) |
Computes the column norm ( 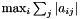 ) of a 2d range. More... ) of a 2d range. More... | |
| template<typename Container2d > | |
| slip::lin_alg_traits< typename Container2d::value_type > ::value_type | col_norm (const Container2d &container) |
Computes the column norm ( 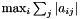 ) of a Container2d. More... ) of a Container2d. More... | |
| template<typename RandomAccessIterator2d > | |
| slip::lin_alg_traits< typename std::iterator_traits < RandomAccessIterator2d > ::value_type >::value_type | frobenius_norm (RandomAccessIterator2d upper_left, RandomAccessIterator2d bottom_right) |
Computes the Frobenius norm ( 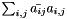 ) of a 2d range. More... ) of a 2d range. More... | |
| template<typename Container2d > | |
| slip::lin_alg_traits< typename Container2d::value_type > ::value_type | frobenius_norm (const Container2d &container) |
Computes the Frobenius norm ( 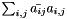 ) of a Container2d. More... ) of a Container2d. More... | |
Diagonal algorithms | |
| template<typename Container2d , typename RandomAccessIterator1 > | |
| void | get_diagonal (const Container2d &container, RandomAccessIterator1 diag_first, RandomAccessIterator1 diag_last, const int diag_number=0) |
| Get the diagonal diag_number of a 2d container. More... | |
| template<typename Container2d , typename RandomAccessIterator1 > | |
| void | set_diagonal (RandomAccessIterator1 diag_first, RandomAccessIterator1 diag_last, Container2d &container, const int diag_number=0) |
| Set the diagonal [diag_first,diag_last) in the diagonal diag_number of a 2d container. More... | |
| template<typename Container2d > | |
| void | fill_diagonal (Container2d &container, const typename Container2d::value_type &val, const int diag_number=0) |
| Fill the diagonal diag_number of a 2d container with the value val. More... | |
| template<typename MatrixIterator > | |
| void | fill_diagonal (MatrixIterator M_up, MatrixIterator M_bot, const typename MatrixIterator::value_type &val, const int diag_number=0) |
| Fill the diagonal diag_number of a 2d range with the value val. More... | |
Matrix generators | |
| template<typename Matrix > | |
| Matrix | identity (const std::size_t nr, const std::size_t nc) |
| Returns an identity matrix which dimensions are nr*nc. More... | |
| template<typename MatrixIterator > | |
| void | identity (MatrixIterator A_up, MatrixIterator A_bot) |
| Set a 2d range to the identity matrix. More... | |
| template<typename Matrix > | |
| void | identity (Matrix &A) |
| Replaces A with the identity matrix. More... | |
| template<typename Matrix > | |
| void | hilbert (Matrix &A) |
| Replaces A with the Hilbert matrix:
. More... | |
| template<typename RandomAccessIterator , typename Matrix > | |
| void | toeplitz (RandomAccessIterator first, RandomAccessIterator last, Matrix &A) |
| Constructs the Toeplitz matrix from given a range. More... | |
Matrix tests | |
| template<typename Matrix > | |
| bool | is_squared (const Matrix &A) |
| Test if a matrix is squared. More... | |
| template<typename MatrixIterator1 > | |
| bool | is_squared (MatrixIterator1 A_up, MatrixIterator1 A_bot) |
| Test if a matrix is squared. More... | |
| template<typename Matrix > | |
| bool | is_identity (const Matrix &A, const typename slip::lin_alg_traits< typename Matrix::value_type >::value_type tol=slip::epsilon< typename Matrix::value_type >()) |
| Test if a matrix is identity. More... | |
| template<typename MatrixIterator1 > | |
| bool | is_diagonal (MatrixIterator1 A_up, MatrixIterator1 A_bot, const typename slip::lin_alg_traits< typename std::iterator_traits< MatrixIterator1 >::value_type >::value_type tol=slip::epsilon< typename std::iterator_traits< MatrixIterator1 >::value_type >()) |
| Test if a matrix is diagonal. More... | |
| template<typename Matrix > | |
| bool | is_diagonal (const Matrix &A, const typename slip::lin_alg_traits< typename Matrix::value_type >::value_type tol=slip::epsilon< typename Matrix::value_type >()) |
| Test if a matrix is diagonal. More... | |
| template<typename MatrixIterator1 > | |
| bool | is_hermitian (MatrixIterator1 A_up, MatrixIterator1 A_bot, const typename slip::lin_alg_traits< typename std::iterator_traits< MatrixIterator1 >::value_type >::value_type tol=slip::epsilon< typename std::iterator_traits< MatrixIterator1 >::value_type >()) |
| Test if a matrix is hermitian. More... | |
| template<typename Matrix > | |
| bool | is_hermitian (const Matrix &A, const typename slip::lin_alg_traits< typename Matrix::value_type >::value_type tol=slip::epsilon< typename Matrix::value_type >()) |
| Test if a matrix is hermitian. More... | |
| template<typename MatrixIterator1 > | |
| bool | is_skew_hermitian (MatrixIterator1 A_up, MatrixIterator1 A_bot, const typename slip::lin_alg_traits< typename std::iterator_traits< MatrixIterator1 >::value_type >::value_type tol=slip::epsilon< typename std::iterator_traits< MatrixIterator1 >::value_type >()) |
| Test if a matrix is skew hermitian. More... | |
| template<typename Matrix > | |
| bool | is_skew_hermitian (const Matrix &A, const typename slip::lin_alg_traits< typename Matrix::value_type >::value_type tol=slip::epsilon< typename Matrix::value_type >()) |
| Test if a matrix is skew hermitian. More... | |
| template<typename MatrixIterator1 > | |
| bool | is_symmetric (MatrixIterator1 A_up, MatrixIterator1 A_bot, const typename slip::lin_alg_traits< typename std::iterator_traits< MatrixIterator1 >::value_type >::value_type tol=slip::epsilon< typename std::iterator_traits< MatrixIterator1 >::value_type >()) |
| Test if a matrix is symmetric. More... | |
| template<typename Matrix > | |
| bool | is_symmetric (const Matrix &A, const typename slip::lin_alg_traits< typename Matrix::value_type >::value_type tol=slip::epsilon< typename Matrix::value_type >()) |
| Test if a matrix is symmetric. More... | |
| template<typename MatrixIterator1 > | |
| bool | is_band_matrix (MatrixIterator1 A_up, MatrixIterator1 A_bot, const typename MatrixIterator1::size_type lower_band_width, const typename MatrixIterator1::size_type upper_band_width, const typename slip::lin_alg_traits< typename std::iterator_traits< MatrixIterator1 >::value_type >::value_type tol=slip::epsilon< typename std::iterator_traits< MatrixIterator1 >::value_type >()) |
| Test if a matrix is a band matrix. More... | |
| template<typename Matrix > | |
| bool | is_band_matrix (const Matrix &A, const typename Matrix::size_type lower_band_width, const typename Matrix::size_type upper_band_width, const typename slip::lin_alg_traits< typename Matrix::value_type >::value_type tol=slip::epsilon< typename Matrix::value_type >()) |
| Test if a matrix is symmetric. More... | |
| template<typename MatrixIterator1 > | |
| bool | is_tridiagonal (MatrixIterator1 A_up, MatrixIterator1 A_bot, const typename slip::lin_alg_traits< typename std::iterator_traits< MatrixIterator1 >::value_type >::value_type tol=slip::epsilon< typename std::iterator_traits< MatrixIterator1 >::value_type >()) |
| Test if a matrix is tridiagonal. More... | |
| template<typename Matrix > | |
| bool | is_tridiagonal (const Matrix &A, const typename slip::lin_alg_traits< typename Matrix::value_type >::value_type tol=slip::epsilon< typename Matrix::value_type >()) |
| Test if a matrix is tridiagonal. More... | |
| template<typename MatrixIterator1 > | |
| bool | is_upper_bidiagonal (MatrixIterator1 A_up, MatrixIterator1 A_bot, const typename slip::lin_alg_traits< typename std::iterator_traits< MatrixIterator1 >::value_type >::value_type tol=slip::epsilon< typename std::iterator_traits< MatrixIterator1 >::value_type >()) |
| Test if a matrix is upper_bidiagonal. More... | |
| template<typename Matrix > | |
| bool | is_upper_bidiagonal (const Matrix &A, const typename slip::lin_alg_traits< typename Matrix::value_type >::value_type tol=slip::epsilon< typename Matrix::value_type >()) |
| Test if a matrix is upper bidiagonal. More... | |
| template<typename MatrixIterator1 > | |
| bool | is_lower_bidiagonal (MatrixIterator1 A_up, MatrixIterator1 A_bot, const typename slip::lin_alg_traits< typename std::iterator_traits< MatrixIterator1 >::value_type >::value_type tol=slip::epsilon< typename std::iterator_traits< MatrixIterator1 >::value_type >()) |
| Test if a matrix is lower_bidiagonal. More... | |
| template<typename Matrix > | |
| bool | is_lower_bidiagonal (const Matrix &A, const typename slip::lin_alg_traits< typename Matrix::value_type >::value_type tol=slip::epsilon< typename Matrix::value_type >()) |
| Test if a matrix is lower bidiagonal. More... | |
| template<typename MatrixIterator1 > | |
| bool | is_upper_hessenberg (MatrixIterator1 A_up, MatrixIterator1 A_bot, const typename slip::lin_alg_traits< typename std::iterator_traits< MatrixIterator1 >::value_type >::value_type tol=slip::epsilon< typename std::iterator_traits< MatrixIterator1 >::value_type >()) |
| Test if a matrix is upper_hessenberg. More... | |
| template<typename Matrix > | |
| bool | is_upper_hessenberg (const Matrix &A, const typename slip::lin_alg_traits< typename Matrix::value_type >::value_type tol=slip::epsilon< typename Matrix::value_type >()) |
| Test if a matrix is upper hessenber. More... | |
| template<typename MatrixIterator1 > | |
| bool | is_lower_hessenberg (MatrixIterator1 A_up, MatrixIterator1 A_bot, const typename slip::lin_alg_traits< typename std::iterator_traits< MatrixIterator1 >::value_type >::value_type tol=slip::epsilon< typename std::iterator_traits< MatrixIterator1 >::value_type >()) |
| Test if a matrix is lower_hessenberg. More... | |
| template<typename Matrix > | |
| bool | is_lower_hessenberg (const Matrix &A, const typename slip::lin_alg_traits< typename Matrix::value_type >::value_type tol=slip::epsilon< typename Matrix::value_type >()) |
| Test if a matrix is lower hessenber. More... | |
| template<typename MatrixIterator1 > | |
| bool | is_upper_triangular (MatrixIterator1 A_up, MatrixIterator1 A_bot, const typename slip::lin_alg_traits< typename std::iterator_traits< MatrixIterator1 >::value_type >::value_type tol=slip::epsilon< typename std::iterator_traits< MatrixIterator1 >::value_type >()) |
| Test if a matrix is upper_triangular. More... | |
| template<typename Matrix > | |
| bool | is_upper_triangular (const Matrix &A, const typename slip::lin_alg_traits< typename Matrix::value_type >::value_type tol=slip::epsilon< typename Matrix::value_type >()) |
| Test if a matrix is upper triangular. More... | |
| template<typename MatrixIterator1 > | |
| bool | is_lower_triangular (MatrixIterator1 A_up, MatrixIterator1 A_bot, const typename slip::lin_alg_traits< typename std::iterator_traits< MatrixIterator1 >::value_type >::value_type tol=slip::epsilon< typename std::iterator_traits< MatrixIterator1 >::value_type >()) |
| Test if a matrix is lower_triangular. More... | |
| template<typename Matrix > | |
| bool | is_lower_triangular (const Matrix &A, const typename slip::lin_alg_traits< typename Matrix::value_type >::value_type tol=slip::epsilon< typename Matrix::value_type >()) |
| Test if a matrix is lower triangular. More... | |
| template<typename MatrixIterator1 > | |
| bool | is_null_diagonal (MatrixIterator1 A_up, MatrixIterator1 A_bot, int diag_number, const typename slip::lin_alg_traits< typename std::iterator_traits< MatrixIterator1 >::value_type >::value_type tol=slip::epsilon< typename std::iterator_traits< MatrixIterator1 >::value_type >()) |
| Test if a matrix has a nul diagonal. More... | |
| template<typename MatrixIterator1 > | |
| slip::DENSE_MATRIX_TYPE | analyse_matrix (MatrixIterator1 A_up, MatrixIterator1 A_bot, const typename slip::lin_alg_traits< typename std::iterator_traits< MatrixIterator1 >::value_type >::value_type tol=slip::epsilon< typename std::iterator_traits< MatrixIterator1 >::value_type >()) |
| Analyse the type of a matrix. More... | |
Pivot algorithms | |
| template<typename MatrixIterator > | |
| int | pivot_max (MatrixIterator M_up, MatrixIterator M_bot) |
| Returns the row position of the maximum partial pivot of a 2d range. More... | |
| template<typename MatrixIterator > | |
| int | partial_pivot (MatrixIterator M_up, MatrixIterator M_bot) |
| Returns the partial pivot of a 2d range. More... | |
General inverse algorithm | |
| template<class Matrix1 , class Matrix2 > | |
| void | inverse (const Matrix1 &M, const std::size_t nr1, const std::size_t nc1, Matrix2 &IM, const std::size_t nr2, const std::size_t nc2) |
| Computes the inverse of a matrix using gaussian elimination. More... | |
| template<class Matrix1 , class Matrix2 > | |
| void | inverse (const Matrix1 &M, Matrix2 &IM) |
| Computes the inverse of a matrix using gaussian elimination. More... | |
LU algorithms | |
| template<class Matrix1 , class Matrix2 , class Vector > | |
| int | lu (const Matrix1 &M, Matrix2 &LU, Vector &Indx) |
| Computes the LU decomposition according to rows permutations of a matrix using Crout method
LU is composed of L and U as following:
Indx is a vector that records the row permutations effected by the partial pivoting. More... | |
| template<class Matrix1 , class Matrix2 > | |
| int | lu (const Matrix1 &M, Matrix2 &L, Matrix2 &U, Matrix2 &P) |
| template<class Matrix , class Vector1 , class Vector2 , class Vector3 > | |
| void | lu_solve (const Matrix LU, const std::size_t nr, const std::size_t nc, const Vector1 &Indx, const std::size_t nv1, const Vector2 &B, const std::size_t nv2, Vector3 &X, const std::size_t nv3) |
| Solve Linear Equation using LU decomposition. More... | |
| template<class Matrix , class Vector1 , class Vector2 > | |
| void | lu_solve (const Matrix &A, Vector1 &X, const Vector2 &B) |
| Solve Linear Equation AX = B using LU decomposition. More... | |
| template<class Matrix1 , class Matrix2 > | |
| void | lu_inv (const Matrix1 &M, Matrix2 &IM) |
| Computes the inverse of a matrix using LU decomposition. More... | |
| template<class Matrix1 > | |
| Matrix1::value_type | lu_det (const Matrix1 &M) |
| Computes the determinant of a matrix using LU decomposition. More... | |
Triangular matrix algorithms | |
| template<typename MatrixIterator , typename RandomAccessIterator1 , typename RandomAccessIterator2 > | |
| void | upper_triangular_solve (MatrixIterator U_up, MatrixIterator U_bot, RandomAccessIterator1 X_first, RandomAccessIterator1 X_last, RandomAccessIterator2 B_first, RandomAccessIterator2 B_last, typename slip::lin_alg_traits< typename MatrixIterator::value_type >::value_type precision) |
| Solve the linear system U*X=B when U is upper triangular
. More... | |
| template<class Matrix , class Vector1 , class Vector2 > | |
| void | upper_triangular_solve (const Matrix &U, Vector1 &X, const Vector2 &B, typename slip::lin_alg_traits< typename Matrix::value_type >::value_type precision) |
| Solve the linear system U*X=B when U is upper triangular
. More... | |
| template<typename MatrixIterator1 , typename MatrixIterator2 > | |
| void | upper_triangular_inv (MatrixIterator1 A_up, MatrixIterator1 A_bot, MatrixIterator2 Ainv_up, MatrixIterator2 Ainv_bot, typename slip::lin_alg_traits< typename MatrixIterator1::value_type >::value_type precision=typename slip::lin_alg_traits< typename MatrixIterator1::value_type >::value_type(1.0E-6)) |
| Invert an upper triangular Matrix
. More... | |
| template<typename Matrix1 , typename Matrix2 > | |
| void | upper_triangular_inv (Matrix1 A, Matrix2 Ainv, typename slip::lin_alg_traits< typename Matrix1::value_type >::value_type precision=typename slip::lin_alg_traits< typename Matrix1::value_type >::value_type(1.0E-6)) |
| Invert an upper triangular Matrix
. More... | |
| template<typename MatrixIterator , typename RandomAccessIterator1 , typename RandomAccessIterator2 > | |
| void | lower_triangular_solve (MatrixIterator L_up, MatrixIterator L_bot, RandomAccessIterator1 X_first, RandomAccessIterator1 X_last, RandomAccessIterator2 B_first, RandomAccessIterator2 B_last, typename slip::lin_alg_traits< typename MatrixIterator::value_type >::value_type precision) |
| Solve the linear system L*X=B when L is lower triangular
. More... | |
| template<class Matrix , class Vector1 , class Vector2 > | |
| void | lower_triangular_solve (const Matrix &L, Vector1 &X, const Vector2 &B, typename slip::lin_alg_traits< typename Matrix::value_type >::value_type precision) |
| Solve the linear system L*X=B when L is lower triangular
. More... | |
| template<typename MatrixIterator1 , typename MatrixIterator2 > | |
| void | lower_triangular_inv (MatrixIterator1 A_up, MatrixIterator1 A_bot, MatrixIterator2 Ainv_up, MatrixIterator2 Ainv_bot, typename slip::lin_alg_traits< typename MatrixIterator1::value_type >::value_type precision=typename slip::lin_alg_traits< typename MatrixIterator1::value_type >::value_type(1.0E-6)) |
| Invert a lower triangular Matrix
. More... | |
| template<typename Matrix1 , typename Matrix2 > | |
| void | lower_triangular_inv (const Matrix1 &A, Matrix2 &Ainv, typename slip::lin_alg_traits< typename Matrix1::value_type >::value_type precision=typename slip::lin_alg_traits< typename Matrix1::value_type >::value_type(1.0E-6)) |
| Invert a lower triangular Matrix
. More... | |
| template<typename MatrixIterator , typename RandomAccessIterator1 , typename RandomAccessIterator2 > | |
| void | unit_upper_triangular_solve (MatrixIterator U_up, MatrixIterator U_bot, RandomAccessIterator1 X_first, RandomAccessIterator1 X_last, RandomAccessIterator2 B_first, RandomAccessIterator2 B_last) |
| Solve the linear system U*X=B when U is unit upper triangular
. More... | |
| template<class Matrix , class Vector1 , class Vector2 > | |
| void | unit_upper_triangular_solve (const Matrix &U, Vector1 &X, const Vector2 &B) |
| Solve the linear system U*X=B when U is unit upper triangular
. More... | |
| template<typename MatrixIterator , typename RandomAccessIterator1 , typename RandomAccessIterator2 > | |
| void | unit_lower_triangular_solve (MatrixIterator L_up, MatrixIterator L_bot, RandomAccessIterator1 X_first, RandomAccessIterator1 X_last, RandomAccessIterator2 B_first, RandomAccessIterator2 B_last) |
| Solve the linear system L*X=B when L is unit lower triangular
. More... | |
| template<class Matrix , class Vector1 , class Vector2 > | |
| void | unit_lower_triangular_solve (const Matrix &L, Vector1 &X, const Vector2 &B) |
| Solve the linear system L*X=B when L is unit lower triangular
. More... | |
Diagonal matrix algorithms | |
| template<typename RandomAccessIterator1 , typename RandomAccessIterator2 , typename RandomAccessIterator3 > | |
| void | diagonal_solve (RandomAccessIterator1 first, RandomAccessIterator1 last, RandomAccessIterator2 X_first, RandomAccessIterator2 X_last, RandomAccessIterator3 B_first, RandomAccessIterator3 B_last, typename slip::lin_alg_traits< typename std::iterator_traits< RandomAccessIterator1 >::value_type >::value_type precision) |
| Solve the linear system D*X=B when D a diagonal matrix
. More... | |
Band matrix algorithms | |
| template<typename MatrixIterator1 , typename RandomAccessIterator > | |
| int | band_lu (MatrixIterator1 A_up, MatrixIterator1 A_bot, const int p, const int q, RandomAccessIterator Ind_first, RandomAccessIterator Ind_last, typename slip::lin_alg_traits< typename MatrixIterator1::value_type >::value_type precision) |
in place Band LU decomposition a square band Matrix A 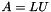 with L a p lower band matrix and U a q upper band matrix More... with L a p lower band matrix and U a q upper band matrix More... | |
| template<class Matrix1 , class Matrix2 , class Matrix3 , class Matrix4 > | |
| int | band_lu (const Matrix1 &M, const int p, const int q, Matrix2 &L, Matrix3 &U, Matrix4 &P, typename slip::lin_alg_traits< typename Matrix1::value_type >::value_type precision) |
in place Band LU decomposition a square band Matrix A 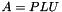 with L a p lower band matrix and U a q upper band matrix and P the permutation matrix. More... with L a p lower band matrix and U a q upper band matrix and P the permutation matrix. More... | |
| template<typename MatrixIterator , typename RandomAccessIterator1 , typename RandomAccessIterator2 > | |
| void | upper_band_solve (MatrixIterator U_up, MatrixIterator U_bot, int q, RandomAccessIterator1 X_first, RandomAccessIterator1 X_last, RandomAccessIterator2 B_first, RandomAccessIterator2 B_last, typename slip::lin_alg_traits< typename MatrixIterator::value_type >::value_type precision) |
| Solve the linear system U*X=B when U is q width upper banded
. More... | |
| template<typename MatrixIterator , typename RandomAccessIterator1 , typename RandomAccessIterator2 > | |
| void | unit_upper_band_solve (MatrixIterator U_up, MatrixIterator U_bot, int q, RandomAccessIterator1 X_first, RandomAccessIterator1 X_last, RandomAccessIterator2 B_first, RandomAccessIterator2 B_last, typename slip::lin_alg_traits< typename MatrixIterator::value_type >::value_type precision) |
| Solve the linear system U*X=B when U is unit q width upper banded
. More... | |
| template<typename MatrixIterator , typename RandomAccessIterator1 , typename RandomAccessIterator2 > | |
| void | lower_band_solve (MatrixIterator L_up, MatrixIterator L_bot, int p, RandomAccessIterator1 X_first, RandomAccessIterator1 X_last, RandomAccessIterator2 B_first, RandomAccessIterator2 B_last, typename slip::lin_alg_traits< typename MatrixIterator::value_type >::value_type precision) |
| Solve the linear system L*X=B when L is p lower banded
. More... | |
| template<typename MatrixIterator , typename RandomAccessIterator1 , typename RandomAccessIterator2 > | |
| void | unit_lower_band_solve (MatrixIterator L_up, MatrixIterator L_bot, int p, RandomAccessIterator1 X_first, RandomAccessIterator1 X_last, RandomAccessIterator2 B_first, RandomAccessIterator2 B_last) |
| Solve the linear system L*X=B when L is unit p lower banded
. More... | |
Gauss system solve algorithms | |
| template<class Matrix , class Vector1 , class Vector2 > | |
| bool | gauss_solve (const Matrix &M, Vector1 &X, const Vector2 &B, typename slip::lin_alg_traits< typename Matrix::value_type >::value_type precision) |
| Solve the linear system M*X=B using the Gauss elemination partial pivoting. More... | |
| template<class Matrix , class Vector1 , class Vector2 > | |
| bool | gauss_solve_with_filling (const Matrix &M, Vector1 &X, const Vector2 &B, typename slip::lin_alg_traits< typename Matrix::value_type >::value_type precision) |
| Solve the linear system M*X=B with the Gauss pivot method, the null pivot are replaced by precision. More... | |
Tridiagonal matrix algorithms | |
| template<typename RandomAccessIterator1 , typename RandomAccessIterator2 , typename RandomAccessIterator3 > | |
| void | tridiagonal_lu (RandomAccessIterator1 diag_first, RandomAccessIterator1 diag_last, RandomAccessIterator1 up_diag_first, RandomAccessIterator1 up_diag_last, RandomAccessIterator1 low_diag_first, RandomAccessIterator1 low_diag_last, RandomAccessIterator2 L_low_first, RandomAccessIterator2 L_low_last, RandomAccessIterator3 U_up_first, RandomAccessIterator3 U_up_last, typename slip::lin_alg_traits< typename std::iterator_traits< RandomAccessIterator1 >::value_type >::value_type precision=typename slip::lin_alg_traits< typename std::iterator_traits< RandomAccessIterator1 >::value_type >::value_type(1.0E-6)) |
| Computes the LU decomposition for a tridiagonal matrix
. More... | |
Bidiagonal matrix algorithms | |
| template<typename RandomAccessIterator1 , typename RandomAccessIterator2 , typename RandomAccessIterator3 > | |
| void | unit_lower_bidiagonal_solve (RandomAccessIterator1 low_diag_first, RandomAccessIterator1 low_diag_last, RandomAccessIterator2 X_first, RandomAccessIterator2 X_last, RandomAccessIterator3 B_first, RandomAccessIterator3 B_last) |
| solve Ax = B with A unit lower bidiagonal
| |
| template<typename RandomAccessIterator1 , typename RandomAccessIterator2d > | |
| void | unit_lower_bidiagonal_inv (RandomAccessIterator1 low_diag_first, RandomAccessIterator1 low_diag_last, RandomAccessIterator2d Ainv_up, RandomAccessIterator2d Ainv_bot) |
| Invert a lower unit bidiagonal matrix:
. More... | |
| template<typename RandomAccessIterator1 , typename RandomAccessIterator2 , typename RandomAccessIterator3 > | |
| void | lower_bidiagonal_solve (RandomAccessIterator1 diag_first, RandomAccessIterator1 diag_last, RandomAccessIterator1 low_diag_first, RandomAccessIterator1 low_diag_last, RandomAccessIterator2 X_first, RandomAccessIterator2 X_last, RandomAccessIterator3 B_first, RandomAccessIterator3 B_last, typename slip::lin_alg_traits< typename std::iterator_traits< RandomAccessIterator1 >::value_type >::value_type precision=typename slip::lin_alg_traits< typename std::iterator_traits< RandomAccessIterator1 >::value_type >::value_type(1.0E-6)) |
| solve Ax = B with A lower bidiagonal
| |
| template<typename RandomAccessIterator1 , typename RandomAccessIterator2d > | |
| void | lower_bidiagonal_inv (RandomAccessIterator1 diag_first, RandomAccessIterator1 diag_last, RandomAccessIterator1 low_diag_first, RandomAccessIterator1 low_diag_last, RandomAccessIterator2d Ainv_up, RandomAccessIterator2d Ainv_bot, typename slip::lin_alg_traits< typename std::iterator_traits< RandomAccessIterator1 >::value_type >::value_type precision=typename slip::lin_alg_traits< typename std::iterator_traits< RandomAccessIterator1 >::value_type >::value_type(1.0E-6)) |
| Invert a lower bidiagonal matrix:
. More... | |
| template<typename Container2d1 , typename Container2d2 > | |
| void | lower_bidiagonal_inv (const Container2d1 &A, Container2d2 &Ainv, typename slip::lin_alg_traits< typename Container2d1::value_type >::value_type precision=typename slip::lin_alg_traits< typename Container2d1::value_type >::value_type(1.0E-6)) |
| Invert a lower bidiagonal matrix:
. More... | |
| template<typename RandomAccessIterator1 , typename RandomAccessIterator2 , typename RandomAccessIterator3 > | |
| void | upper_bidiagonal_solve (RandomAccessIterator1 diag_first, RandomAccessIterator1 diag_last, RandomAccessIterator1 up_diag_first, RandomAccessIterator1 up_diag_last, RandomAccessIterator2 X_first, RandomAccessIterator2 X_last, RandomAccessIterator3 B_first, RandomAccessIterator3 B_last, typename slip::lin_alg_traits< typename std::iterator_traits< RandomAccessIterator1 >::value_type >::value_type precision=typename slip::lin_alg_traits< typename std::iterator_traits< RandomAccessIterator1 >::value_type >::value_type(1.0E-6)) |
| solve Ax = B with A upper bidiagonal
| |
| template<typename RandomAccessIterator1 , typename RandomAccessIterator2d > | |
| void | upper_bidiagonal_inv (RandomAccessIterator1 diag_first, RandomAccessIterator1 diag_last, RandomAccessIterator1 up_diag_first, RandomAccessIterator1 up_diag_last, RandomAccessIterator2d Ainv_up, RandomAccessIterator2d Ainv_bot, typename slip::lin_alg_traits< typename std::iterator_traits< RandomAccessIterator1 >::value_type >::value_type precision=typename slip::lin_alg_traits< typename std::iterator_traits< RandomAccessIterator1 >::value_type >::value_type(1.0E-6)) |
| Invert an upper bidiagonal squared matrix
. More... | |
| template<typename Container2d1 , typename Container2d2 > | |
| void | upper_bidiagonal_inv (const Container2d1 &A, Container2d2 &Ainv, typename slip::lin_alg_traits< typename Container2d1::value_type >::value_type precision=typename slip::lin_alg_traits< typename Container2d1::value_type >::value_type(1.0E-6)) |
| Invert an upper bidiagonal squared matrix
. More... | |
| template<typename RandomAccessIterator1 , typename RandomAccessIterator2 , typename RandomAccessIterator3 > | |
| void | unit_upper_bidiagonal_solve (RandomAccessIterator1 up_diag_first, RandomAccessIterator1 up_diag_last, RandomAccessIterator2 X_first, RandomAccessIterator2 X_last, RandomAccessIterator3 B_first, RandomAccessIterator3 B_last) |
| solve Ax = B with A unit upper bidiagonal
| |
| template<typename RandomAccessIterator1 , typename RandomAccessIterator2d > | |
| void | unit_upper_bidiagonal_inv (RandomAccessIterator1 up_diag_first, RandomAccessIterator1 up_diag_last, RandomAccessIterator2d Ainv_up, RandomAccessIterator2d Ainv_bot) |
| Invert an unit upper bidiagonal matrix:
. More... | |
Tridiagonal system solve algorithms | |
| template<typename RandomAccessIterator1 , typename RandomAccessIterator2 , typename RandomAccessIterator3 > | |
| void | thomas_solve (RandomAccessIterator1 diag_first, RandomAccessIterator1 diag_last, RandomAccessIterator1 up_diag_first, RandomAccessIterator1 up_diag_last, RandomAccessIterator1 low_diag_first, RandomAccessIterator1 low_diag_last, RandomAccessIterator2 X_first, RandomAccessIterator2 X_last, RandomAccessIterator3 B_first, RandomAccessIterator3 B_last, typename slip::lin_alg_traits< typename std::iterator_traits< RandomAccessIterator1 >::value_type >::value_type precision=typename slip::lin_alg_traits< typename std::iterator_traits< RandomAccessIterator1 >::value_type >::value_type(1.0E-6)) |
| Solve the tridiagonal system A*X=B with the Thomas method
. More... | |
| template<typename Container2d , typename Vector1 , typename Vector2 > | |
| void | thomas_solve (const Container2d &A, Vector1 &X, const Vector2 &B, typename slip::lin_alg_traits< typename Container2d::value_type >::value_type precision=typename slip::lin_alg_traits< typename Container2d::value_type >::value_type(1.0E-6)) |
| Solve the tridiagonal system Tx=B
. More... | |
| template<typename RandomAccessIterator1 , typename RandomAccessIterator2d > | |
| void | thomas_inv (RandomAccessIterator1 diag_first, RandomAccessIterator1 diag_last, RandomAccessIterator1 up_diag_first, RandomAccessIterator1 up_diag_last, RandomAccessIterator1 low_diag_first, RandomAccessIterator1 low_diag_last, RandomAccessIterator2d Ainv_up, RandomAccessIterator2d Ainv_bot, typename slip::lin_alg_traits< typename std::iterator_traits< RandomAccessIterator1 >::value_type >::value_type precision=typename slip::lin_alg_traits< typename std::iterator_traits< RandomAccessIterator1 >::value_type >::value_type(1.0E-6)) |
| Invert a tridiagonal squared matrix A with the Thomas method
. More... | |
| template<typename Container2d1 , typename Container2d2 > | |
| void | thomas_inv (const Container2d1 &A, Container2d2 &Ainv, typename slip::lin_alg_traits< typename Container2d1::value_type >::value_type precision=typename slip::lin_alg_traits< typename Container2d1::value_type >::value_type(1.0E-6)) |
| Invert a tridiagonal squared matrix A with the Thomas method
. More... | |
Tridiagonal symmetric positive matrix algorithms | |
| template<typename RandomAccessIterator1 , typename RandomAccessIterator2 , typename RandomAccessIterator3 > | |
| void | tridiagonal_cholesky (RandomAccessIterator1 diag_first, RandomAccessIterator1 diag_last, RandomAccessIterator1 up_diag_first, RandomAccessIterator1 up_diag_last, RandomAccessIterator2 R_diag_first, RandomAccessIterator2 R_diag_last, RandomAccessIterator3 R_low_first, RandomAccessIterator3 R_low_last) |
| Tridiagonal symmetric positive decomposition
where: | |
| template<typename RandomAccessIterator1 , typename RandomAccessIterator2 , typename RandomAccessIterator3 > | |
| void | tridiagonal_cholesky_solve (RandomAccessIterator1 diag_first, RandomAccessIterator1 diag_last, RandomAccessIterator1 up_diag_first, RandomAccessIterator1 up_diag_last, RandomAccessIterator2 X_first, RandomAccessIterator2 X_last, RandomAccessIterator3 B_first, RandomAccessIterator3 B_last) |
| Solve the tridiagonal symmetric positive definite system T*X=B with the Cholesky method
where: | |
| template<typename Container2d , typename Vector1 , typename Vector2 > | |
| void | tridiagonal_cholesky_solve (const Container2d &A, Vector1 &X, const Vector2 &B) |
| Solve the tridiagonal symmetric positive definite system T*X=B with the Cholesky method
where: | |
| template<typename RandomAccessIterator1 , typename RandomAccessIterator2d > | |
| void | tridiagonal_cholesky_inv (RandomAccessIterator1 diag_first, RandomAccessIterator1 diag_last, RandomAccessIterator1 up_diag_first, RandomAccessIterator1 up_diag_last, RandomAccessIterator2d Ainv_up, RandomAccessIterator2d Ainv_bot) |
| Invert the tridiagonal symmetric positive definite system T:
where: | |
| template<typename Container2d1 , typename Container2d2 > | |
| void | tridiagonal_cholesky_inv (const Container2d1 &A, Container2d2 &Ainv) |
| Invert the tridiagonal symmetric positive definite system T:
where: | |
LDLT algorithms | |
| template<typename Container2d > | |
| void | LDLT_decomposition (Container2d &A) |
| in place LU decomposition for symmetric matrix
| |
| template<typename Matrix1 , typename Matrix2 , typename Vector1 , typename Matrix3 > | |
| void | LDLT_decomposition (const Matrix1 &A, Matrix2 &L, Vector1 &D, Matrix3 <) |
| in place LU decomposition for symmetric matrix
| |
| template<typename Matrix1 , typename Vector1 , typename Vector2 > | |
| void | LDLT_solve (const Matrix1 &A, Vector1 &X, const Vector2 &B) |
LDLT solve of system AX = B with A a square symmetric Matrix. 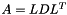 with L a lower triangular matrix. More... with L a lower triangular matrix. More... | |
Square hermitian or symmetric matrix algorithms | |
| template<typename MatrixIterator1 , typename MatrixIterator2 , typename MatrixIterator3 > | |
| void | cholesky_cplx (MatrixIterator1 A_up, MatrixIterator1 A_bot, MatrixIterator2 L_up, MatrixIterator2 L_bot, MatrixIterator3 LH_up, MatrixIterator3 LH_bot) |
cholesky decomposition of a square hermitian positive definite Matrix. 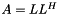 with L a lower triangular matrix More... with L a lower triangular matrix More... | |
| template<typename MatrixIterator1 > | |
| void | cholesky_cplx (MatrixIterator1 A_up, MatrixIterator1 A_bot) |
cholesky decomposition of a square hermitian positive definite Matrix. 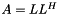 with L a lower triangular matrix. L is stored in the lower triangular part of A, with L a lower triangular matrix. L is stored in the lower triangular part of A, 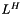 is stored in the upper triangular part of A. More... is stored in the upper triangular part of A. More... | |
| template<typename MatrixIterator1 , typename MatrixIterator2 , typename MatrixIterator3 > | |
| void | cholesky_real (MatrixIterator1 A_up, MatrixIterator1 A_bot, MatrixIterator2 L_up, MatrixIterator2 L_bot, MatrixIterator3 LH_up, MatrixIterator3 LH_bot) |
cholesky decomposition of a square real symmetric and positive definite Matrix. 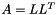 with L a lower triangular matrix. More... with L a lower triangular matrix. More... | |
| template<typename MatrixIterator1 > | |
| void | cholesky_real (MatrixIterator1 A_up, MatrixIterator1 A_bot) |
cholesky decomposition of a square real symmetric and positive definite Matrix. 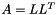 with L a lower triangular matrix. L is stored in the lower triangular part of A, with L a lower triangular matrix. L is stored in the lower triangular part of A, 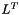 is stored in the upper triangular part of A. More... is stored in the upper triangular part of A. More... | |
| template<class Matrix1 , class Matrix2 , class Matrix3 > | |
| void | cholesky_real (const Matrix1 &A, Matrix2 &L, Matrix3 <) |
cholesky decomposition of a square real symmetric positive definite Matrix. 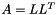 with L a lower triangular matrix More... with L a lower triangular matrix More... | |
| template<class Matrix1 , class Matrix2 , class Matrix3 > | |
| void | cholesky_cplx (const Matrix1 &A, Matrix2 &L, Matrix3 <) |
cholesky decomposition of a square hermitian positive definite Matrix. 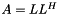 with L a lower triangular matrix More... with L a lower triangular matrix More... | |
| template<class Matrix1 , class Matrix2 , class Matrix3 > | |
| void | cholesky (const Matrix1 &A, Matrix2 &L, Matrix3 <) |
cholesky decomposition of a square hermitian positive definite Matrix. 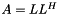 with L a lower triangular matrix More... with L a lower triangular matrix More... | |
| template<class Matrix1 > | |
| void | cholesky (Matrix1 &A) |
cholesky decomposition of a square hermitian positive definite Matrix. 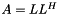 with L a lower triangular matrix. L is stored in the lower triangular part of A, with L a lower triangular matrix. L is stored in the lower triangular part of A, 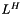 is stored in the upper triangular part of A. More... is stored in the upper triangular part of A. More... | |
| template<typename MatrixIterator , typename RandomAccessIterator1 , typename RandomAccessIterator2 > | |
| void | cholesky_solve (MatrixIterator A_up, MatrixIterator A_bot, RandomAccessIterator1 X_first, RandomAccessIterator1 X_last, RandomAccessIterator2 B_first, RandomAccessIterator2 B_last, typename slip::lin_alg_traits< typename MatrixIterator::value_type >::value_type precision=typename slip::lin_alg_traits< typename MatrixIterator::value_type >::value_type(1.0E-6)) |
| cholesky solve of system AX = B with A a square hermitian positive definite Matrix. More... | |
| template<class Matrix1 , class Vector1 , class Vector2 > | |
| void | cholesky_solve (const Matrix1 &A, Vector1 &X, const Vector2 &B, typename slip::lin_alg_traits< typename Matrix1::value_type >::value_type precision=typename slip::lin_alg_traits< typename Matrix1::value_type >::value_type(1.0E-6)) |
| cholesky solve of system AX = B with A a square hermitian positive definite Matrix. More... | |
| template<typename MatrixIterator1 , typename MatrixIterator2 > | |
| void | cholesky_inv (MatrixIterator1 A_up, MatrixIterator1 A_bot, MatrixIterator2 Ainv_up, MatrixIterator2 Ainv_bot, typename slip::lin_alg_traits< typename MatrixIterator1::value_type >::value_type precision=typename slip::lin_alg_traits< typename MatrixIterator1::value_type >::value_type(1.0E-6)) |
| cholesky inverse of a square hermitian positive definite Matrix A. More... | |
| template<typename Matrix1 , typename Matrix2 > | |
| void | cholesky_inv (Matrix1 A, Matrix2 Ainv, typename slip::lin_alg_traits< typename Matrix1::value_type >::value_type precision=typename slip::lin_alg_traits< typename Matrix1::value_type >::value_type(1.0E-6)) |
| cholesky inverse of a square hermitian positive definite Matrix A. More... | |
Givens rotations algorithms | |
| template<typename Real > | |
| void | rotgen (Real &a, Real &b, Real &cos, Real &sin) |
| Computes the Givens sinus and cosinus. More... | |
| template<typename Real > | |
| void | givens_sin_cos (const Real &xi, const Real &xk, Real &sin, Real &cos) |
| Computes the Givens sinus and cosinus.
. More... | |
| template<typename Complex > | |
| void | complex_givens_sin_cos (const Complex &xi, const Complex &xk, Complex &sin, typename Complex::value_type &cos) |
| Computes the complex Givens sinus and cosinus.
with
. More... | |
| template<typename Matrix , typename SizeType , typename Real > | |
| void | left_givens (Matrix &M, const SizeType &row1, const SizeType &row2, const Real &sinus, const Real &cosinus, const SizeType &col1, const SizeType &col2) |
| Apply left Givens rotation multiplication. More... | |
| template<typename Matrix , typename SizeType , typename Real > | |
| void | right_givens (Matrix &M, const SizeType &col1, const SizeType &col2, const Real &sinus, const Real &cosinus, const SizeType &row1, const SizeType &row2) |
| Apply right Givens rotation multiplication. More... | |
| template<typename Matrix , typename SizeType , typename Complex > | |
| void | complex_left_givens (Matrix &M, const SizeType &row1, const SizeType &row2, const Complex &sinus, const typename Complex::value_type &cosinus, const SizeType &col1, const SizeType &col2) |
| Apply complex left Givens rotation multiplication. More... | |
| template<typename Matrix , typename SizeType , typename Complex > | |
| void | complex_right_givens (Matrix &M, const SizeType &col1, const SizeType &col2, const Complex &sinus, const typename Complex::value_type &cosinus, const SizeType &row1, const SizeType &row2) |
| Apply complex right Givens rotation multiplication. More... | |
Householder algorithms | |
| template<typename VectorIterator1 , typename VectorIterator2 > | |
| void | housegen (VectorIterator1 a_begin, VectorIterator1 a_end, VectorIterator2 u_begin, VectorIterator2 u_end, typename std::iterator_traits< VectorIterator1 >::value_type &nu) |
| Compute the Householder vector u of a vector a. More... | |
| template<typename RandomAccessIterator , typename MatrixIterator1 > | |
| void | right_householder_update (RandomAccessIterator V_first, RandomAccessIterator V_last, MatrixIterator1 M_up, MatrixIterator1 M_bot) |
| right multiplies the matrix M with the Householder matrix P:
| |
| template<typename RandomAccessIterator , typename MatrixIterator1 > | |
| void | left_householder_update (RandomAccessIterator V_first, RandomAccessIterator V_last, MatrixIterator1 M_up, MatrixIterator1 M_bot) |
| Left multiplies the Householder matrix P with the matrix M:
. More... | |
| template<typename Matrix1 , typename Vector1 , typename Matrix2 > | |
| void | left_householder_accumulate (const Matrix1 &M, const Vector1 &V0, Matrix2 &Q) |
| Computes Q = Q1Q2...Qn from the inplace Householder QR decomposition. More... | |
Hessenberg reduction | |
| template<typename Matrix1 > | |
| void | householder_hessenberg (Matrix1 &M) |
Householder Hessenberg reduction of the square matrix M. The result is overwritten in M. The Hessenberg decomposition is 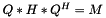 . More... . More... | |
| template<typename Matrix1 , typename Matrix2 > | |
| void | householder_hessenberg (const Matrix1 &M, Matrix2 &H) |
Householder Hessenberg reduction of the square matrix M. The Hessenberg decomposition is 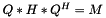 . More... . More... | |
| template<typename Matrix1 , typename Matrix2 , typename Matrix3 > | |
| void | householder_hessenberg (const Matrix1 &M, Matrix2 &H, Matrix3 &Q) |
Householder Hessenberg reduction of the square matrix M. The Hessenberg decomposition is 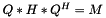 . More... . More... | |
SVD internal algorithms | |
| template<typename Matrix1 , typename Vector , typename Matrix2 , typename Matrix3 > | |
| void | BiReduce (Matrix1 &X, Vector &d, Vector &e, Matrix2 &U, Matrix3 &V) |
| BiReduce. Given an n*p matrix X with n>=p Bireduce reduce X to an upper bidiagola form The tranformations from the left are accumulmated in the n*p matrix U and the transformations from the right in the matrix V. on return X contains the genrators of the householder transformation used in the reduction X=U[d,e]V. More... | |
| template<typename Matrix , typename Vector > | |
| void | Bi_complex_to_real (Vector &d, Vector &e, Matrix &U, Matrix &V) |
| BiQR Given an upper bidiagonal matrix B, Bi_complex_to_real transforms the complex bidiagonal form into a real form. The tranformations from the left are accumulmated in the matrix U and the transformations from the right in the matrix V. More... | |
| template<typename Matrix , typename Vector , typename Real , typename SizeType > | |
| void | BiQR (Vector &d, Vector &e, Real &sigma, const SizeType &row1, const SizeType &row2, Matrix &U, Matrix &V) |
| BiQR Given an upper bidiagonal matrix B and a shift sigma, BiQR performs a QR step between rows row1 ans row2. The tranformations from the left are accumulmated in the matrix U and the transformations from the right in the matrix V. More... | |
| template<typename Real > | |
| void | shift (Real &p, Real &r, Real &q, Real &sigma) |
| Given a matrix
compute the smallest singular value of this matrix. More... | |
| template<typename Vector , typename SizeType > | |
| void | BdBacksearch (Vector &d, Vector &e, const typename slip::lin_alg_traits< typename Vector::value_type >::value_type tol, SizeType &l, SizeType &i1, SizeType &i2) |
| Back searching a bidiagonal Matrix this algorithm takes a bidiagobal matrix B, a tolerance tol and an index l(0<=l<=p-1) and determines indices i1,i2<=l such one of the following condictions holds 1) 0<=i1<i2<=l, in which case the matrix deflates as rows i1 and i2. 2) 0=i1=i2, in which case all the superdiagonal elements of B in rows 0 through l-1 are zero. More... | |
SVD Decomposition algorithms | |
| template<typename Matrix1 , typename Matrix2 , typename RandomAccessIterator , typename Matrix3 > | |
| void | svd (const Matrix1 &M, Matrix2 &U, RandomAccessIterator S_first, RandomAccessIterator S_last, Matrix3 &V, const int max_it=75) |
| (thin) Singular Value Decomposition Given a matrix M, this function computes its singular value decomposition, Any n*p matrix M whose number of rows n is greater than or equal to its number of columns p, can be written as the product of an n*p column-orthogonal matrix Up, an p*p diagonal matrix S with positive or zero elements (the singular values), and the hermitian transpose of an p*p orthogonal matrix V
| |
| template<typename Matrix , typename Matrix2 > | |
| void | svd (const Matrix &X, Matrix &U, Matrix2 &S, Matrix &V, const int max_it=75) |
| (thin) Singular Value Decomposition Given a matrix M, this function computes its singular value decomposition, Any n*p matrix M whose number of rows n is greater than or equal to its number of columns p, can be written as the product of an n*p column-orthogonal matrix Up, an p*p diagonal matrix S with positive or zero elements (the singular values), and the transpose of an p*p orthogonal matrix V
| |
SVD approximation algorithms | |
| template<typename Matrix1 , typename RandomAccessIterator , typename Matrix2 , typename Matrix3 > | |
| void | svd_approx (const Matrix1 &U, RandomAccessIterator S_first, RandomAccessIterator S_last, const Matrix2 &V, const std::size_t K, Matrix3 &X) |
Singular Value Approximation of a matrix from its Singular Value Decomposition given by U, W and V: 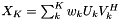 . More... . More... | |
| template<class Matrix1 , class Matrix2 , class Matrix3 , class Matrix4 > | |
| void | svd_approx (const Matrix1 &U, const Matrix2 &W, const Matrix3 &V, const std::size_t K, Matrix4 &M) |
Singular Value Approximation of a matrix from its Singular Value Decomposition given by U, W and V: 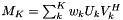 . More... . More... | |
SVD system solve algorithms | |
| template<class Matrix1 , typename RandomAccessIterator1 , class Matrix2 , typename RandomAccessIterator2 , typename RandomAccessIterator3 > | |
| void | svd_solve (const Matrix1 &U, RandomAccessIterator1 W_first, RandomAccessIterator1 W_last, const Matrix2 &V, RandomAccessIterator2 B_first, RandomAccessIterator2 B_last, RandomAccessIterator3 X_first, RandomAccessIterator3 X_last) |
| Solve Linear (USV^H).X = B where U, S and V are provided by a svd decomposition. More... | |
| template<class Matrix1 , typename RandomAccessIterator1 , typename RandomAccessIterator2 > | |
| void | svd_solve (const Matrix1 &A, RandomAccessIterator1 X_first, RandomAccessIterator1 X_last, RandomAccessIterator2 B_first, RandomAccessIterator2 B_last) |
| Solve Linear Equation A.X = B using SVD decomposition. More... | |
| template<class Matrix1 , class Vector1 , class Vector2 > | |
| void | svd_solve (const Matrix1 &A, Vector1 &X, const Vector2 &B) |
| Solve Linear Equation A.X = B using SVD decomposition. More... | |
SVD inverse algorithms | |
| template<class Matrix1 , typename RandomAccessIterator1 , class Matrix2 , class Matrix3 > | |
| void | svd_inv (const Matrix1 &U, RandomAccessIterator1 W_first, RandomAccessIterator1 W_last, const Matrix2 &V, Matrix3 &Ainv) |
| Singular Value inverse of a matrix from its Singular Value Decomposition given by U, W and V. More... | |
| template<class Matrix1 , class Matrix2 > | |
| void | svd_inv (const Matrix1 &A, Matrix2 &Ainv) |
| Singular Value inverse of a matrix. More... | |
| template<class Matrix1 , class Matrix2 > | |
| void | pinv (const Matrix1 &A, Matrix2 &Ainv) |
| Pseudo inverse of a matrix. More... | |
1d linear least square algorithms | |
| template<typename RandomAccessIterator1 , typename RandomAccessIterator2 , typename RandomAccessIterator3 , typename RandomAccessIterator4 > | |
| double | svd_least_square (RandomAccessIterator1 x_first, RandomAccessIterator1 x_last, RandomAccessIterator2 y_first, RandomAccessIterator3 s_first, RandomAccessIterator4 p_first, RandomAccessIterator4 p_last, slip::EvalBasis< typename std::iterator_traits< RandomAccessIterator1 >::value_type, RandomAccessIterator2 > &basis_fun) |
| Linear Least Square fitting using SVD. More... | |
| template<typename Vector1 , typename Vector2 , typename Vector3 , typename Vector4 > | |
| double | svd_least_square (Vector1 &X, Vector2 &Y, Vector3 &S, Vector4 &P, slip::EvalBasis< typename Vector1::value_type, typename Vector2::iterator > &basis_fun) |
| Linear Least Square fitting using SVD. More... | |
| template<typename RandomAccessIterator1 , typename RandomAccessIterator2 , typename RandomAccessIterator3 > | |
| double | svd_least_square (RandomAccessIterator1 x_first, RandomAccessIterator1 x_last, RandomAccessIterator2 y_first, RandomAccessIterator3 p_first, RandomAccessIterator3 p_last, slip::EvalBasis< typename std::iterator_traits< RandomAccessIterator1 >::value_type, RandomAccessIterator2 > &basis_fun) |
| Linear Least Square fitting using SVD. More... | |
| template<typename Vector1 , typename Vector2 , typename Vector3 > | |
| double | svd_least_square (Vector1 &X, Vector2 &Y, Vector3 &P, slip::EvalBasis< typename Vector1::value_type, typename Vector2::iterator > &basis_fun) |
| Linear Least Square fitting using SVD. More... | |
Multidimensional linear least square algorithms | |
| template<typename RandomAccessIterator1 , typename RandomAccessIterator2 , typename RandomAccessIterator3 , typename RandomAccessIterator4 > | |
| double | svd_least_square_nd (RandomAccessIterator1 x_first, RandomAccessIterator1 x_last, RandomAccessIterator2 y_first, RandomAccessIterator3 s_first, RandomAccessIterator4 p_first, RandomAccessIterator4 p_last, const std::size_t order, slip::EvalBasis< typename std::iterator_traits< RandomAccessIterator1 >::value_type, RandomAccessIterator2 > &basis_fun) |
| nd Linear Least Square fitting using SVD. More... | |
| template<typename RandomAccessIterator1 , typename RandomAccessIterator2 , typename RandomAccessIterator3 > | |
| double | svd_least_square_nd (RandomAccessIterator1 x_first, RandomAccessIterator1 x_last, RandomAccessIterator2 y_first, RandomAccessIterator3 p_first, RandomAccessIterator3 p_last, const std::size_t order, slip::EvalBasis< typename std::iterator_traits< RandomAccessIterator1 >::value_type, RandomAccessIterator2 > &basis_fun) |
| nd Linear Least Square fitting using SVD. More... | |
| template<typename Vector1 , typename Vector2 , typename Vector3 > | |
| double | svd_least_square_nd (Vector1 &X, Vector2 &Y, Vector3 &P, const std::size_t order, slip::EvalBasis< typename Vector1::value_type, typename Vector2::iterator > &basis_fun) |
| nd Linear Least Square fitting using SVD. More... | |
Gaussian noise algorithms | |
| template<typename InputIterator , typename OutputIterator , typename Real > | |
| void | add_gaussian_noise (InputIterator first, InputIterator last, OutputIterator result, const Real mean=Real(0.0), const Real var=Real(0.01)) |
| Add a gaussian noise to a container. More... | |
| template<typename InputIterator , typename OutputIterator , typename Real , typename MaskIterator > | |
| void | add_gaussian_noise_mask (InputIterator first, InputIterator last, MaskIterator mask_first, OutputIterator result, const Real mean=Real(0.0), const Real var=Real(0.01), typename std::iterator_traits< MaskIterator >::value_type value=typename std::iterator_traits< MaskIterator >::value_type(1)) |
| Add a gaussian noise to a container according to a mask sequence. More... | |
| template<typename InputIterator , typename OutputIterator , typename Real , typename Predicate > | |
| void | add_gaussian_noise_if (InputIterator first, InputIterator last, OutputIterator result, Predicate pred, const Real mean=Real(0.0), const Real var=Real(0.01)) |
| Add a gaussian noise to a container according to a predicate. More... | |
Speckle noise algorithms | |
| template<typename InputIterator , typename OutputIterator , typename Real > | |
| void | add_speckle_noise (InputIterator first, InputIterator last, OutputIterator result, const Real var=0.04) |
| Add a speckle noise to a container. More... | |
| template<typename InputIterator , typename OutputIterator , typename Real , typename MaskIterator > | |
| void | add_speckle_noise_mask (InputIterator first, InputIterator last, MaskIterator mask_first, OutputIterator result, const Real var=0.04, typename std::iterator_traits< MaskIterator >::value_type value=typename std::iterator_traits< MaskIterator >::value_type(1)) |
| Add a speckle noise to a container according to a mask sequence. More... | |
| template<typename InputIterator , typename OutputIterator , typename Real , typename Predicate > | |
| void | add_speckle_noise_if (InputIterator first, InputIterator last, OutputIterator result, Predicate pred, const Real var=0.04) |
| Add a speckle noise to a container according to a predicate. More... | |
Uniform noise algorithms | |
| template<typename InputIterator , typename OutputIterator , typename Real > | |
| void | add_uniform_noise (InputIterator first, InputIterator last, OutputIterator result, const Real min=Real(0.0), const Real max=Real(1.0)) |
| Add a uniform noise to a container. More... | |
| template<typename InputIterator , typename OutputIterator , typename Real , typename MaskIterator > | |
| void | add_uniform_noise_mask (InputIterator first, InputIterator last, MaskIterator mask_first, OutputIterator result, const Real min=Real(0.0), const Real max=Real(1.0), typename std::iterator_traits< MaskIterator >::value_type value=typename std::iterator_traits< MaskIterator >::value_type(1)) |
| Add a uniform noise to a container according to mask sequence. More... | |
| template<typename InputIterator , typename OutputIterator , typename Real , typename Predicate > | |
| void | add_uniform_noise_if (InputIterator first, InputIterator last, OutputIterator result, Predicate pred, const Real min=Real(0.0), const Real max=Real(1.0)) |
| Add a uniform noise to a container according to a predicate. More... | |
Salt and pepper noise algorithms | |
| template<typename InputIterator , typename OutputIterator , typename Real > | |
| void | add_salt_and_pepper_noise (InputIterator first, InputIterator last, OutputIterator result, const Real density=Real(0.05), const typename std::iterator_traits< OutputIterator >::value_type salt_value=typename std::iterator_traits< OutputIterator >::value_type(1.0), const typename std::iterator_traits< OutputIterator >::value_type pepper_value=typename std::iterator_traits< OutputIterator >::value_type(0.0)) |
| Add a salt and pepper noise to a container. More... | |
| template<typename InputIterator , typename OutputIterator , typename Real , typename MaskIterator > | |
| void | add_salt_and_pepper_noise_mask (InputIterator first, InputIterator last, MaskIterator mask_first, OutputIterator result, const Real density=Real(0.05), const Real salt_value=Real(1.0), const Real pepper_value=Real(0.0), typename std::iterator_traits< MaskIterator >::value_type value=typename std::iterator_traits< MaskIterator >::value_type(1)) |
| Add a salt and pepper noise to a container according to a mask sequence. More... | |
| template<typename InputIterator , typename OutputIterator , typename Real , typename Predicate > | |
| void | add_salt_and_pepper_noise_if (InputIterator first, InputIterator last, OutputIterator result, Predicate pred, const Real density=Real(0.05), const Real salt_value=Real(1.0), const Real pepper_value=Real(0.0)) |
| Add a salt and pepper noise to a container according to a predicate. More... | |
Legendre polynomial algorithms | |
| template<typename Poly , typename Poly1 , typename Poly2 , typename Poly3 > | |
| Poly | legendre_nd_next (std::size_t k, Poly1 x, Poly2 Pk, Poly3 Pkm1) |
| Implements the three term recurrence relation for the Legendre multivariate polynomials, this function can be used to create a sequence of orthogonal polynomial, and for rising k. This recurrence relation holds for Legendre Polynomials of both the first and second kinds:
. More... | |
| template<typename Poly , typename Poly1 , typename Poly2 , typename Poly3 > | |
| Poly | legendre_next (std::size_t k, Poly1 x, Poly2 Pk, Poly3 Pkm1) |
| Implements the three term recurrence relation for the Legendre polynomials, this function can be used to create a sequence of orthogonal polynomial, and for rising k. This recurrence relation holds for Legendre Polynomials of both the first and second kinds:
. More... | |
Chebyshev polynomial algorithms | |
| template<typename Poly , typename Poly1 , typename Poly2 , typename Poly3 > | |
| Poly | chebyshev_next (std::size_t k, Poly1 x, Poly2 Pk, Poly3 Pkm1) |
| Implements the three term recurrence relation for the Chebyshev polynomials, this function can be used to create a sequence of orthogonal polynomial, and for rising k. This recurrence relation holds for Chebyshev Polynomials of both the first and second kinds:
. More... | |
| template<typename Poly , typename Poly1 , typename Poly2 , typename Poly3 > | |
| Poly | chebyshev_nd_next (std::size_t k, Poly1 x, Poly2 Pk, Poly3 Pkm1) |
| Implements the three term recurrence relation for the Chebyshev multivariate polynomials, this function can be used to create a sequence of orthogonal polynomial, and for rising k. This recurrence relation holds for Chebychev Polynomials of both the first and second kinds:
. More... | |
| template<typename T , typename RandomAccessIterator > | |
| void | eval_chebyshevII_basis (const T &x, const std::size_t n, RandomAccessIterator first, RandomAccessIterator last) |
| Returns the evaluations of x until order n to the range [first,last) using the ChebyshevII scheme. The order of the resulting values is the following (1,2x,4x^2-1,8x^3-4x,...). More... | |
| template<typename T , typename RandomAccessIterator > | |
| void | eval_discrete_chebyshev_basis (const T &x, const std::size_t n, RandomAccessIterator first, RandomAccessIterator last) |
| Returns the evaluations of x until order n to the range [first,last) using the Discrete Chebyshev scheme. The order of the resulting values is the following (1,2x-N+1,...). More... | |
Hermite polynomial algorithms | |
| template<typename Poly , typename Poly1 , typename Poly2 , typename Poly3 > | |
| Poly | hermite_next (std::size_t k, Poly1 x, Poly2 Pk, Poly3 Pkm1) |
| Implements the three term recurrence relation for the Hermite polynomials, this function can be used to create a sequence of orthogonal polynomial, and for rising k. This recurrence relation holds for Hermite Polynomials:
. More... | |
| template<typename Poly , typename Poly1 , typename Poly2 , typename Poly3 > | |
| Poly | hermite_nd_next (std::size_t k, Poly1 x, Poly2 Pk, Poly3 Pkm1) |
| Implements the three term recurrence relation for the Hermite multivariate polynomials, this function can be used to create a sequence of orthogonal polynomial, and for rising k. This recurrence relation holds for Hermite Polynomials:
. More... | |
| template<typename T , typename RandomAccessIterator > | |
| void | eval_hermite_basis (const T &x, const std::size_t n, RandomAccessIterator first, RandomAccessIterator last) |
| Returns the evaluations of x until order n to the range [first,last) using the Hermite scheme. The order of the resulting values is the following (1,2x,4x^2-2,8x^3-12x,...). More... | |
Laguerre polynomial algorithms | |
| template<typename Poly , typename Poly1 , typename Poly2 , typename Poly3 > | |
| Poly | laguerre_next (std::size_t k, Poly1 x, Poly2 Pk, Poly3 Pkm1) |
| Implements the three term recurrence relation for the Laguerre polynomials, this function can be used to create a sequence of orthogonal polynomial, and for rising k. This recurrence relation holds for Laguerre Polynomials:
. More... | |
| template<typename Poly , typename Poly1 , typename Poly2 , typename Poly3 > | |
| Poly | laguerre_nd_next (std::size_t k, Poly1 x, Poly2 Pk, Poly3 Pkm1) |
| Implements the three term recurrence relation for the Laguerre multivariate polynomials, this function can be used to create a sequence of orthogonal polynomial, and for rising k. This recurrence relation holds for Laguere Polynomials:
. More... | |
| template<typename T , typename RandomAccessIterator > | |
| void | eval_laguerre_basis (const T &x, const std::size_t n, RandomAccessIterator first, RandomAccessIterator last) |
| Returns the evaluations of x until order n to the range [first,last) using the Laguerre scheme. The order of the resulting values is the following (1,-x+1,0.5x^2-2x+1,-(1/6)x^3-(3/2)x^2-3x+1,...). More... | |
Polynome evaluation algorithms | |
| template<typename T , typename RandomAccessIterator > | |
| T | eval_horner (RandomAccessIterator first, RandomAccessIterator last, const T &x) |
| Returns the evaluation of the polynomial given throw the range [first,last) at x using the horner scheme. The coefficients of the polynomial a0 + a1x + a2x^2 +... anx^n are supposed ordered as follows : (a0,a1,...,an). More... | |
| template<typename T , typename RandomAccessIterator > | |
| void | eval_power_basis (const T &x, const std::size_t n, RandomAccessIterator first, RandomAccessIterator last) |
| Returns the evaluation of the power of x until order n to the range [first,last) using the horner scheme. More... | |
| template<typename T , typename RandomAccessIterator > | |
| void | eval_legendre_basis (const T &x, const std::size_t n, RandomAccessIterator first, RandomAccessIterator last) |
| Returns the evaluations of x until order n to the range [first,last) using the legendre scheme. More... | |
| template<typename T , typename RandomAccessIterator > | |
| void | eval_chebyshev_basis (const T &x, const std::size_t n, RandomAccessIterator first, RandomAccessIterator last) |
| Returns the evaluations of x until order n to the range [first,last) using the Chebyshev scheme. More... | |
| template<class Vector , typename RandomAccessIterator > | |
| void | eval_power_2d_basis (const Vector &x, const std::size_t n, RandomAccessIterator first, RandomAccessIterator last) |
Returns the evaluation of the powers of X = (x1,x2) such that 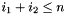 with with 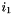 and and 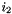 the power of x1 and x2. the range [first,last) using the horner scheme. More... the power of x1 and x2. the range [first,last) using the horner scheme. More... | |
| template<class Vector , typename RandomAccessIterator > | |
| void | eval_power_nd_basis (const Vector &x, const std::size_t order, RandomAccessIterator first, RandomAccessIterator last) |
Returns the evaluation of the powers of 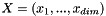 such that such that 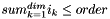 with with 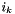 the power of the xk to the range [first,last) using the horner scheme. More... the power of the xk to the range [first,last) using the horner scheme. More... | |
| template<typename MultivariatePolynomial , typename RandomAccessIterator > | |
| void | eval_multi_poly_power_basis (const MultivariatePolynomial &x, const std::size_t n, RandomAccessIterator first, RandomAccessIterator last) |
| Returns the evaluation of the power of a slip::MultivariatePolynomial<T,DIM> P until order n to the range [first,last) using the horner scheme. More... | |
| template<class Vector , typename RandomAccessIterator > | |
| void | eval_multi_poly_power_nd_basis (const Vector &x, const std::size_t order, RandomAccessIterator first, RandomAccessIterator last) |
Returns the evaluation of the powers of slip::MultivariatePolynomial<T,DIM> 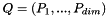 such that such that  with with  the power of the qk to the range [first,last) using the horner scheme. More... the power of the qk to the range [first,last) using the horner scheme. More... | |
recursive statistics algorithms | |
| template<typename DataT , typename MeanT > | |
| MeanT | mean_next (const int n, const MeanT &prev_mean, const DataT &xnp1) |
| Recursive mean algorithm. More... | |
| template<typename DataT , typename VarT > | |
| void | var_next (const int n, const VarT &prev_mean, const VarT &prev_var, const DataT &xnp1, VarT &next_mean, VarT &next_var) |
| Recursive variance algorithm. More... | |
Transform algorithms | |
| template<typename _InputIterator , typename _MaskIterator , typename _OutputIterator , typename _UnaryOperation > | |
| _OutputIterator | transform_mask_un (_InputIterator first, _InputIterator last, _MaskIterator mask_first, _OutputIterator result, _UnaryOperation unary_op, typename std::iterator_traits< _MaskIterator >::value_type value=typename std::iterator_traits< _MaskIterator >::value_type(1)) |
| Perform an operation on a sequence according to a mask sequence. More... | |
| template<typename _InputIterator1 , typename _InputIterator2 , typename _MaskIterator , typename _OutputIterator , typename _BinaryOperation > | |
| _OutputIterator | transform_mask_bin (_InputIterator1 first1, _InputIterator1 last1, _MaskIterator mask_first, _InputIterator2 first2, _OutputIterator result, _BinaryOperation binary_op, typename std::iterator_traits< _MaskIterator >::value_type value=typename std::iterator_traits< _MaskIterator >::value_type(1)) |
| Perform an operation on corresponding elements of two sequences according to a mask sequence. More... | |
| template<typename _InputIterator , typename _OutputIterator , typename _UnaryOperation , typename _Predicate > | |
| _OutputIterator | transform_if (_InputIterator first, _InputIterator last, _OutputIterator result, _UnaryOperation unary_op, _Predicate pred) |
| Perform an operation on a sequence according to a Predicate. More... | |
| template<typename _InputIterator1 , typename _InputIterator2 , typename _OutputIterator , typename _BinaryOperation , typename _Predicate > | |
| _OutputIterator | transform_if (_InputIterator1 first1, _InputIterator1 last1, _InputIterator2 first2, _OutputIterator result, _BinaryOperation binary_op, _Predicate pred) |
| Perform an operation on corresponding elements of two sequences according to a Predicate. More... | |
max_element algorithms | |
| template<typename _ForwardIterator , typename _MaskIterator > | |
| _ForwardIterator | max_element_mask (_ForwardIterator first, _ForwardIterator last, _MaskIterator mask_first, typename std::iterator_traits< _MaskIterator >::value_type value=typename std::iterator_traits< _MaskIterator >::value_type(1)) |
| Return the maximum element in a range according to a mask sequence or return last if no value verify the mask. More... | |
| template<typename _ForwardIterator , typename Predicate > | |
| _ForwardIterator | max_element_if (_ForwardIterator first, _ForwardIterator last, Predicate pred) |
| Return the maximum element in a range according to a predicate or last if the predicate is never verified. More... | |
| template<typename _ForwardIterator , typename _MaskIterator , typename _Compare > | |
| _ForwardIterator | max_element_mask_compare (_ForwardIterator first, _ForwardIterator last, _MaskIterator mask_first, _Compare comp, typename std::iterator_traits< _MaskIterator >::value_type value=typename std::iterator_traits< _MaskIterator >::value_type(1)) |
| Return the maximum element in a range using comparison functor according to a mask sequence or return last if no value verify the mask. More... | |
| template<typename _ForwardIterator , typename _Compare , typename Predicate > | |
| _ForwardIterator | max_element_if_compare (_ForwardIterator first, _ForwardIterator last, Predicate pred, _Compare comp) |
| Return the maximum element in a range using comparison functor according to a predicate or return last if the predicate is never verified. More... | |
min_element algorithms | |
| template<typename _ForwardIterator , typename _MaskIterator > | |
| _ForwardIterator | min_element_mask (_ForwardIterator first, _ForwardIterator last, _MaskIterator mask_first, typename std::iterator_traits< _MaskIterator >::value_type value=typename std::iterator_traits< _MaskIterator >::value_type(1)) |
| Return the minimum element in a range according to a mask sequence or return last if no value verify the mask. More... | |
| template<typename _ForwardIterator , typename _MaskIterator , typename _Compare > | |
| _ForwardIterator | min_element_mask_compare (_ForwardIterator first, _ForwardIterator last, _MaskIterator mask_first, _Compare comp, typename std::iterator_traits< _MaskIterator >::value_type value=typename std::iterator_traits< _MaskIterator >::value_type(1)) |
| Return the minimum element in a range using comparison functor according to a mask sequence or return last if no value verify the mask. More... | |
| template<typename _ForwardIterator , typename Predicate > | |
| _ForwardIterator | min_element_if (_ForwardIterator first, _ForwardIterator last, Predicate pred) |
| Return the minimum element in a range according to a predicate or return last if the predicate is never verified. More... | |
| template<typename _ForwardIterator , typename _Compare , typename Predicate > | |
| _ForwardIterator | min_element_if_compare (_ForwardIterator first, _ForwardIterator last, Predicate pred, _Compare comp) |
| Return the minimum element in a range using comparison functor according to a predicate or return last if the predicate is never verified. More... | |
input/output operators | |
| template<typename T > | |
| std::ostream & | operator<< (std::ostream &out, const Array< T > &a) |
| template<typename T > | |
| std::ostream & | operator<< (std::ostream &out, const slip::Array2d< T > &a) |
| template<typename T > | |
| std::ostream & | operator<< (std::ostream &out, const slip::Array3d< T > &a) |
| template<typename T > | |
| std::ostream & | operator<< (std::ostream &out, const slip::Array4d< T > &a) |
| template<typename T , std::size_t N> | |
| std::ostream & | operator<< (std::ostream &out, const block< T, N > &b) |
| template<typename T , std::size_t NR, std::size_t NC> | |
| std::ostream & | operator<< (std::ostream &out, const slip::block2d< T, NR, NC > &b) |
| template<typename T , std::size_t NP, std::size_t NR, std::size_t NC> | |
| std::ostream & | operator<< (std::ostream &out, const slip::block3d< T, NP, NR, NC > &b) |
| template<typename T , std::size_t NS, std::size_t NP, std::size_t NR, std::size_t NC> | |
| std::ostream & | operator<< (std::ostream &out, const slip::block4d< T, NS, NP, NR, NC > &b) |
| template<typename T > | |
| std::ostream & | operator<< (std::ostream &out, const Color< T > &b) |
| template<typename T > | |
| std::ostream & | operator<< (std::ostream &out, const Colormap< T > &a) |
EqualityComparable functions | |
| template<typename T > | |
| bool | operator== (const Array< T > &x, const Array< T > &y) |
| template<typename T > | |
| bool | operator!= (const Array< T > &x, const Array< T > &y) |
| template<typename T > | |
| bool | operator== (const slip::Array2d< T > &x, const slip::Array2d< T > &y) |
| template<typename T > | |
| bool | operator!= (const slip::Array2d< T > &x, const slip::Array2d< T > &y) |
| template<typename T > | |
| bool | operator== (const slip::Array3d< T > &x, const slip::Array3d< T > &y) |
| template<typename T > | |
| bool | operator!= (const slip::Array3d< T > &x, const slip::Array3d< T > &y) |
| template<typename T > | |
| bool | operator== (const slip::Array4d< T > &x, const slip::Array4d< T > &y) |
| template<typename T > | |
| bool | operator!= (const slip::Array4d< T > &x, const slip::Array4d< T > &y) |
| template<typename T , std::size_t N> | |
| bool | operator== (const block< T, N > &x, const block< T, N > &y) |
| template<typename T , std::size_t N> | |
| bool | operator!= (const block< T, N > &x, const block< T, N > &y) |
| template<typename T , std::size_t NR, std::size_t NC> | |
| bool | operator== (const slip::block2d< T, NR, NC > &x, const slip::block2d< T, NR, NC > &y) |
| template<typename T , std::size_t NR, std::size_t NC> | |
| bool | operator!= (const slip::block2d< T, NR, NC > &x, const slip::block2d< T, NR, NC > &y) |
| template<typename T , std::size_t NP, std::size_t NR, std::size_t NC> | |
| bool | operator== (const slip::block3d< T, NP, NR, NC > &x, const slip::block3d< T, NP, NR, NC > &y) |
| template<typename T , std::size_t NP, std::size_t NR, std::size_t NC> | |
| bool | operator!= (const slip::block3d< T, NP, NR, NC > &x, const slip::block3d< T, NP, NR, NC > &y) |
| template<typename T , std::size_t NS, std::size_t NP, std::size_t NR, std::size_t NC> | |
| bool | operator== (const slip::block4d< T, NS, NP, NR, NC > &x, const slip::block4d< T, NS, NP, NR, NC > &y) |
| template<typename T , std::size_t NS, std::size_t NP, std::size_t NR, std::size_t NC> | |
| bool | operator!= (const slip::block4d< T, NS, NP, NR, NC > &x, const slip::block4d< T, NS, NP, NR, NC > &y) |
| template<typename T > | |
| bool | operator== (const Colormap< T > &x, const Colormap< T > &y) |
| template<typename T > | |
| bool | operator!= (const Colormap< T > &x, const Colormap< T > &y) |
| template<typename T > | |
| bool | operator== (const slip::GrayscaleImage< T > &x, const slip::GrayscaleImage< T > &y) |
| template<typename T > | |
| bool | operator!= (const slip::GrayscaleImage< T > &x, const slip::GrayscaleImage< T > &y) |
| template<typename T > | |
| bool | operator== (const slip::HyperVolume< T > &x, const slip::HyperVolume< T > &y) |
| template<typename T > | |
| bool | operator!= (const slip::HyperVolume< T > &x, const slip::HyperVolume< T > &y) |
| template<typename T > | |
| bool | operator== (const slip::Matrix< T > &x, const slip::Matrix< T > &y) |
| template<typename T > | |
| bool | operator!= (const slip::Matrix< T > &x, const slip::Matrix< T > &y) |
| template<std::size_t DIM> | |
| bool | operator== (const Monomial< DIM > &x, const Monomial< DIM > &y) |
| template<std::size_t DIM> | |
| bool | operator!= (const Monomial< DIM > &x, const Monomial< DIM > &y) |
| template<typename T > | |
| bool | operator== (const Polynomial< T > &x, const Polynomial< T > &y) |
| template<typename T > | |
| bool | operator!= (const Polynomial< T > &x, const Polynomial< T > &y) |
| template<typename T > | |
| bool | operator== (const Signal< T > &x, const Signal< T > &y) |
| template<typename T > | |
| bool | operator!= (const Signal< T > &x, const Signal< T > &y) |
| template<typename T > | |
| bool | operator== (const Vector< T > &x, const Vector< T > &y) |
| template<typename T > | |
| bool | operator!= (const Vector< T > &x, const Vector< T > &y) |
| template<typename T > | |
| bool | operator== (const slip::Volume< T > &x, const slip::Volume< T > &y) |
| template<typename T > | |
| bool | operator!= (const slip::Volume< T > &x, const slip::Volume< T > &y) |
LessThanComparable functions | |
| template<typename T > | |
| bool | operator< (const Array< T > &x, const Array< T > &y) |
| template<typename T > | |
| bool | operator> (const Array< T > &x, const Array< T > &y) |
| template<typename T > | |
| bool | operator<= (const Array< T > &x, const Array< T > &y) |
| template<typename T > | |
| bool | operator>= (const Array< T > &x, const Array< T > &y) |
| template<typename T > | |
| bool | operator< (const slip::Array2d< T > &x, const slip::Array2d< T > &y) |
| template<typename T > | |
| bool | operator> (const slip::Array2d< T > &x, const slip::Array2d< T > &y) |
| template<typename T > | |
| bool | operator<= (const slip::Array2d< T > &x, const slip::Array2d< T > &y) |
| template<typename T > | |
| bool | operator>= (const slip::Array2d< T > &x, const slip::Array2d< T > &y) |
| template<typename T > | |
| bool | operator< (const slip::Array3d< T > &x, const slip::Array3d< T > &y) |
| template<typename T > | |
| bool | operator> (const slip::Array3d< T > &x, const slip::Array3d< T > &y) |
| template<typename T > | |
| bool | operator<= (const slip::Array3d< T > &x, const slip::Array3d< T > &y) |
| template<typename T > | |
| bool | operator>= (const slip::Array3d< T > &x, const slip::Array3d< T > &y) |
| template<typename T > | |
| bool | operator< (const slip::Array4d< T > &x, const slip::Array4d< T > &y) |
| template<typename T > | |
| bool | operator> (const slip::Array4d< T > &x, const slip::Array4d< T > &y) |
| template<typename T > | |
| bool | operator<= (const slip::Array4d< T > &x, const slip::Array4d< T > &y) |
| template<typename T > | |
| bool | operator>= (const slip::Array4d< T > &x, const slip::Array4d< T > &y) |
| template<typename T , std::size_t N> | |
| bool | operator< (const block< T, N > &x, const block< T, N > &y) |
| template<typename T , std::size_t N> | |
| bool | operator> (const block< T, N > &x, const block< T, N > &y) |
| template<typename T , std::size_t N> | |
| bool | operator<= (const block< T, N > &x, const block< T, N > &y) |
| template<typename T , std::size_t N> | |
| bool | operator>= (const block< T, N > &x, const block< T, N > &y) |
| template<typename T , std::size_t NR, std::size_t NC> | |
| bool | operator< (const slip::block2d< T, NR, NC > &x, const slip::block2d< T, NR, NC > &y) |
| template<typename T , std::size_t NR, std::size_t NC> | |
| bool | operator> (const slip::block2d< T, NR, NC > &x, const slip::block2d< T, NR, NC > &y) |
| template<typename T , std::size_t NR, std::size_t NC> | |
| bool | operator<= (const slip::block2d< T, NR, NC > &x, const slip::block2d< T, NR, NC > &y) |
| template<typename T , std::size_t NR, std::size_t NC> | |
| bool | operator>= (const slip::block2d< T, NR, NC > &x, const slip::block2d< T, NR, NC > &y) |
| template<typename T , std::size_t NP, std::size_t NR, std::size_t NC> | |
| bool | operator< (const slip::block3d< T, NP, NR, NC > &x, const slip::block3d< T, NP, NR, NC > &y) |
| template<typename T , std::size_t NP, std::size_t NR, std::size_t NC> | |
| bool | operator> (const slip::block3d< T, NP, NR, NC > &x, const slip::block3d< T, NP, NR, NC > &y) |
| template<typename T , std::size_t NP, std::size_t NR, std::size_t NC> | |
| bool | operator<= (const slip::block3d< T, NP, NR, NC > &x, const slip::block3d< T, NP, NR, NC > &y) |
| template<typename T , std::size_t NP, std::size_t NR, std::size_t NC> | |
| bool | operator>= (const slip::block3d< T, NP, NR, NC > &x, const slip::block3d< T, NP, NR, NC > &y) |
| template<typename T , std::size_t NS, std::size_t NP, std::size_t NR, std::size_t NC> | |
| bool | operator< (const slip::block4d< T, NS, NP, NR, NC > &x, const slip::block4d< T, NS, NP, NR, NC > &y) |
| template<typename T , std::size_t NS, std::size_t NP, std::size_t NR, std::size_t NC> | |
| bool | operator> (const slip::block4d< T, NS, NP, NR, NC > &x, const slip::block4d< T, NS, NP, NR, NC > &y) |
| template<typename T , std::size_t NS, std::size_t NP, std::size_t NR, std::size_t NC> | |
| bool | operator<= (const slip::block4d< T, NS, NP, NR, NC > &x, const slip::block4d< T, NS, NP, NR, NC > &y) |
| template<typename T , std::size_t NS, std::size_t NP, std::size_t NR, std::size_t NC> | |
| bool | operator>= (const slip::block4d< T, NS, NP, NR, NC > &x, const slip::block4d< T, NS, NP, NR, NC > &y) |
| template<typename T > | |
| bool | operator< (const slip::GrayscaleImage< T > &x, const slip::GrayscaleImage< T > &y) |
| template<typename T > | |
| bool | operator> (const slip::GrayscaleImage< T > &x, const slip::GrayscaleImage< T > &y) |
| template<typename T > | |
| bool | operator<= (const slip::GrayscaleImage< T > &x, const slip::GrayscaleImage< T > &y) |
| template<typename T > | |
| bool | operator>= (const slip::GrayscaleImage< T > &x, const slip::GrayscaleImage< T > &y) |
| template<typename T > | |
| bool | operator< (const slip::HyperVolume< T > &x, const slip::HyperVolume< T > &y) |
| template<typename T > | |
| bool | operator> (const slip::HyperVolume< T > &x, const slip::HyperVolume< T > &y) |
| template<typename T > | |
| bool | operator<= (const slip::HyperVolume< T > &x, const slip::HyperVolume< T > &y) |
| template<typename T > | |
| bool | operator>= (const slip::HyperVolume< T > &x, const slip::HyperVolume< T > &y) |
| template<typename T > | |
| bool | operator< (const slip::Matrix< T > &x, const slip::Matrix< T > &y) |
| template<typename T > | |
| bool | operator> (const slip::Matrix< T > &x, const slip::Matrix< T > &y) |
| template<typename T > | |
| bool | operator<= (const slip::Matrix< T > &x, const slip::Matrix< T > &y) |
| template<typename T > | |
| bool | operator>= (const slip::Matrix< T > &x, const slip::Matrix< T > &y) |
| template<typename T > | |
| bool | operator< (const Polynomial< T > &x, const Polynomial< T > &y) |
| template<typename T > | |
| bool | operator> (const Polynomial< T > &x, const Polynomial< T > &y) |
| template<typename T > | |
| bool | operator<= (const Polynomial< T > &x, const Polynomial< T > &y) |
| template<typename T > | |
| bool | operator>= (const Polynomial< T > &x, const Polynomial< T > &y) |
| template<typename T > | |
| bool | operator< (const Signal< T > &x, const Signal< T > &y) |
| template<typename T > | |
| bool | operator> (const Signal< T > &x, const Signal< T > &y) |
| template<typename T > | |
| bool | operator<= (const Signal< T > &x, const Signal< T > &y) |
| template<typename T > | |
| bool | operator>= (const Signal< T > &x, const Signal< T > &y) |
| template<typename T > | |
| bool | operator< (const Vector< T > &x, const Vector< T > &y) |
| template<typename T > | |
| bool | operator> (const Vector< T > &x, const Vector< T > &y) |
| template<typename T > | |
| bool | operator<= (const Vector< T > &x, const Vector< T > &y) |
| template<typename T > | |
| bool | operator>= (const Vector< T > &x, const Vector< T > &y) |
| template<typename T > | |
| bool | operator< (const Vector2d< T > &x, const Vector2d< T > &y) |
| template<typename T > | |
| bool | operator> (const Vector2d< T > &x, const Vector2d< T > &y) |
| template<typename T > | |
| bool | operator<= (const Vector2d< T > &x, const Vector2d< T > &y) |
| template<typename T > | |
| bool | operator>= (const Vector2d< T > &x, const Vector2d< T > &y) |
| template<typename T > | |
| bool | operator< (const Vector3d< T > &x, const Vector3d< T > &y) |
| template<typename T > | |
| bool | operator> (const Vector3d< T > &x, const Vector3d< T > &y) |
| template<typename T > | |
| bool | operator<= (const Vector3d< T > &x, const Vector3d< T > &y) |
| template<typename T > | |
| bool | operator>= (const Vector3d< T > &x, const Vector3d< T > &y) |
| template<typename T > | |
| bool | operator< (const Vector4d< T > &x, const Vector4d< T > &y) |
| template<typename T > | |
| bool | operator> (const Vector4d< T > &x, const Vector4d< T > &y) |
| template<typename T > | |
| bool | operator<= (const Vector4d< T > &x, const Vector4d< T > &y) |
| template<typename T > | |
| bool | operator>= (const Vector4d< T > &x, const Vector4d< T > &y) |
| template<typename T > | |
| bool | operator< (const slip::Volume< T > &x, const slip::Volume< T > &y) |
| template<typename T > | |
| bool | operator> (const slip::Volume< T > &x, const slip::Volume< T > &y) |
| template<typename T > | |
| bool | operator<= (const slip::Volume< T > &x, const slip::Volume< T > &y) |
| template<typename T > | |
| bool | operator>= (const slip::Volume< T > &x, const slip::Volume< T > &y) |
EqualityComparable Color functions | |
| template<typename T > | |
| bool | operator== (const Color< T > &x, const Color< T > &y) |
| template<typename T > | |
| bool | operator!= (const Color< T > &x, const Color< T > &y) |
Color arithmetic operations | |
| template<typename T > | |
| Color< T > | operator+ (const Color< T > &V1, const Color< T > &V2) |
| template<typename T > | |
| Color< T > | operator+ (const Color< T > &V1, const T &val) |
| template<typename T > | |
| Color< T > | operator+ (const T &val, const Color< T > &V1) |
| template<typename T > | |
| Color< T > | operator- (const Color< T > &V1, const Color< T > &V2) |
| template<typename T > | |
| Color< T > | operator- (const Color< T > &V1, const T &val) |
| template<typename T > | |
| Color< T > | operator- (const T &val, const Color< T > &V1) |
| template<typename T > | |
| Color< T > | operator* (const Color< T > &V1, const Color< T > &V2) |
| template<typename T > | |
| Color< T > | operator* (const Color< T > &V1, const T &val) |
| template<typename T > | |
| Color< T > | operator* (const T &val, const Color< T > &V1) |
| template<typename T > | |
| Color< T > | operator/ (const Color< T > &V1, const Color< T > &V2) |
| template<typename T > | |
| Color< T > | operator/ (const Color< T > &V1, const T &val) |
Arithmetical DenseVector2dField2d operators | |
| template<typename T > | |
| DenseVector2dField2d< T > | operator+ (const DenseVector2dField2d< T > &M1, const T &val) |
| addition of a scalar to each element of a DenseVector2dField2d More... | |
| template<typename T > | |
| DenseVector2dField2d< T > | operator+ (const T &val, const DenseVector2dField2d< T > &M1) |
| addition of a scalar to each element of a DenseVector2dField2d More... | |
| template<typename T > | |
| DenseVector2dField2d< T > | operator- (const DenseVector2dField2d< T > &M1, const T &val) |
| substraction of a scalar to each element of a DenseVector2dField2d More... | |
| template<typename T > | |
| DenseVector2dField2d< T > | operator- (const T &val, const DenseVector2dField2d< T > &M1) |
| substraction of a scalar to each element of a DenseVector2dField2d More... | |
| template<typename T > | |
| DenseVector2dField2d< T > | operator* (const DenseVector2dField2d< T > &M1, const T &val) |
| multiplication of a scalar to each element of a DenseVector2dField2d More... | |
| template<typename T > | |
| DenseVector2dField2d< T > | operator* (const T &val, const DenseVector2dField2d< T > &M1) |
| multiplication of a scalar to each element of a DenseVector2dField2d More... | |
| template<typename T > | |
| DenseVector2dField2d< T > | operator/ (const DenseVector2dField2d< T > &M1, const T &val) |
| division of a scalar to each element of a DenseVector2dField2d More... | |
| template<typename T > | |
| DenseVector2dField2d< T > | operator+ (const DenseVector2dField2d< T > &M1, const DenseVector2dField2d< T > &M2) |
| pointwise addition of two DenseVector2dField2d More... | |
| template<typename T > | |
| DenseVector2dField2d< T > | operator+ (const DenseVector2dField2d< T > &M1, const slip::Vector2d< T > &val) |
| addition of a Vector2d to each element of a DenseVector2dField2d More... | |
| template<typename T > | |
| DenseVector2dField2d< T > | operator+ (const slip::Vector2d< T > &val, const DenseVector2dField2d< T > &M1) |
| addition of a Vector2d to each element of a DenseVector2dField2d More... | |
| template<typename T > | |
| DenseVector2dField2d< T > | operator- (const DenseVector2dField2d< T > &M1, const DenseVector2dField2d< T > &M2) |
| pointwise substraction of two DenseVector2dField2d More... | |
| template<typename T > | |
| DenseVector2dField2d< T > | operator- (const DenseVector2dField2d< T > &M1, const slip::Vector2d< T > &val) |
| substraction of a Vector2d to each element of a DenseVector2dField2d More... | |
| template<typename T > | |
| DenseVector2dField2d< T > | operator- (const slip::Vector2d< T > &val, const DenseVector2dField2d< T > &M1) |
| substraction of a Vector2d to each element of a DenseVector2dField2d More... | |
| template<typename T > | |
| DenseVector2dField2d< T > | operator* (const DenseVector2dField2d< T > &M1, const DenseVector2dField2d< T > &M2) |
| pointwise multiplication of two DenseVector2dField2d More... | |
| template<typename T > | |
| DenseVector2dField2d< T > | operator* (const DenseVector2dField2d< T > &M1, const slip::Vector2d< T > &val) |
| multiplication of a Vector2d to each element of a DenseVector2dField2d More... | |
| template<typename T > | |
| DenseVector2dField2d< T > | operator* (const slip::Vector2d< T > &val, const DenseVector2dField2d< T > &M1) |
| multiplication of a Vector2d to each element of a DenseVector2dField2d More... | |
| template<typename T > | |
| DenseVector2dField2d< T > | operator/ (const DenseVector2dField2d< T > &M1, const DenseVector2dField2d< T > &M2) |
| pointwise division of two DenseVector2dField2d More... | |
| template<typename T > | |
| DenseVector2dField2d< T > | operator/ (const DenseVector2dField2d< T > &M1, const slip::Vector2d< T > &val) |
| division of a Vector2d to each element of a DenseVector2dField2d More... | |
Arithmetical DenseVector3dField2d operators | |
| template<typename T > | |
| DenseVector3dField2d< T > | operator+ (const DenseVector3dField2d< T > &M1, const T &val) |
| addition of a scalar to each element of a DenseVector3dField2d More... | |
| template<typename T > | |
| DenseVector3dField2d< T > | operator+ (const T &val, const DenseVector3dField2d< T > &M1) |
| addition of a scalar to each element of a DenseVector3dField2d More... | |
| template<typename T > | |
| DenseVector3dField2d< T > | operator- (const DenseVector3dField2d< T > &M1, const T &val) |
| substraction of a scalar to each element of a DenseVector3dField2d More... | |
| template<typename T > | |
| DenseVector3dField2d< T > | operator- (const T &val, const DenseVector3dField2d< T > &M1) |
| substraction of a scalar to each element of a DenseVector3dField2d More... | |
| template<typename T > | |
| DenseVector3dField2d< T > | operator* (const DenseVector3dField2d< T > &M1, const T &val) |
| multiplication of a scalar to each element of a DenseVector3dField2d More... | |
| template<typename T > | |
| DenseVector3dField2d< T > | operator* (const T &val, const DenseVector3dField2d< T > &M1) |
| multiplication of a scalar to each element of a DenseVector3dField2d More... | |
| template<typename T > | |
| DenseVector3dField2d< T > | operator/ (const DenseVector3dField2d< T > &M1, const T &val) |
| division of a scalar to each element of a DenseVector3dField2d More... | |
| template<typename T > | |
| DenseVector3dField2d< T > | operator+ (const DenseVector3dField2d< T > &M1, const DenseVector3dField2d< T > &M2) |
| pointwise addition of two DenseVector3dField2d More... | |
| template<typename T > | |
| DenseVector3dField2d< T > | operator+ (const DenseVector3dField2d< T > &M1, const slip::Vector3d< T > &val) |
| addition of a Vector3d to each element of a DenseVector3dField2d More... | |
| template<typename T > | |
| DenseVector3dField2d< T > | operator+ (const slip::Vector3d< T > &val, const DenseVector3dField2d< T > &M1) |
| addition of a Vector3d to each element of a DenseVector3dField2d More... | |
| template<typename T > | |
| DenseVector3dField2d< T > | operator- (const DenseVector3dField2d< T > &M1, const DenseVector3dField2d< T > &M2) |
| pointwise substraction of two DenseVector3dField2d More... | |
| template<typename T > | |
| DenseVector3dField2d< T > | operator- (const DenseVector3dField2d< T > &M1, const slip::Vector3d< T > &val) |
| substraction of a Vector3d to each element of a DenseVector3dField2d More... | |
| template<typename T > | |
| DenseVector3dField2d< T > | operator- (const slip::Vector3d< T > &val, const DenseVector3dField2d< T > &M1) |
| substraction of a Vector3d to each element of a DenseVector3dField2d More... | |
| template<typename T > | |
| DenseVector3dField2d< T > | operator* (const DenseVector3dField2d< T > &M1, const DenseVector3dField2d< T > &M2) |
| pointwise multiplication of two DenseVector3dField2d More... | |
| template<typename T > | |
| DenseVector3dField2d< T > | operator* (const DenseVector3dField2d< T > &M1, const slip::Vector3d< T > &val) |
| multiplication of a Vector3d to each element of a DenseVector3dField2d More... | |
| template<typename T > | |
| DenseVector3dField2d< T > | operator* (const slip::Vector3d< T > &val, const DenseVector3dField2d< T > &M1) |
| multiplication of a Vector3d to each element of a DenseVector3dField2d More... | |
| template<typename T > | |
| DenseVector3dField2d< T > | operator/ (const DenseVector3dField2d< T > &M1, const DenseVector3dField2d< T > &M2) |
| pointwise division of two DenseVector3dField2d More... | |
| template<typename T > | |
| DenseVector3dField2d< T > | operator/ (const DenseVector3dField2d< T > &M1, const slip::Vector3d< T > &val) |
| division of a Vector3d to each element of a DenseVector3dField2d More... | |
Arithmetical DenseVector3dField3d operators | |
| template<typename T > | |
| DenseVector3dField3d< T > | operator+ (const DenseVector3dField3d< T > &M1, const T &val) |
| addition of a scalar to each element of a DenseVector3dField3d More... | |
| template<typename T > | |
| DenseVector3dField3d< T > | operator+ (const T &val, const DenseVector3dField3d< T > &M1) |
| addition of a scalar to each element of a DenseVector3dField3d More... | |
| template<typename T > | |
| DenseVector3dField3d< T > | operator- (const DenseVector3dField3d< T > &M1, const T &val) |
| substraction of a scalar to each element of a DenseVector3dField3d More... | |
| template<typename T > | |
| DenseVector3dField3d< T > | operator- (const T &val, const DenseVector3dField3d< T > &M1) |
| substraction of a scalar to each element of a DenseVector3dField3d More... | |
| template<typename T > | |
| DenseVector3dField3d< T > | operator* (const DenseVector3dField3d< T > &M1, const T &val) |
| multiplication of a scalar to each element of a DenseVector3dField3d More... | |
| template<typename T > | |
| DenseVector3dField3d< T > | operator* (const T &val, const DenseVector3dField3d< T > &M1) |
| multiplication of a scalar to each element of a DenseVector3dField3d More... | |
| template<typename T > | |
| DenseVector3dField3d< T > | operator/ (const DenseVector3dField3d< T > &M1, const T &val) |
| division of a scalar to each element of a DenseVector3dField3d More... | |
| template<typename T > | |
| DenseVector3dField3d< T > | operator+ (const DenseVector3dField3d< T > &M1, const DenseVector3dField3d< T > &M2) |
| pointwise addition of two DenseVector3dField3d More... | |
| template<typename T > | |
| DenseVector3dField3d< T > | operator+ (const DenseVector3dField3d< T > &M1, const slip::Vector3d< T > &val) |
| addition of a Vector3d to each element of a DenseVector3dField3d More... | |
| template<typename T > | |
| DenseVector3dField3d< T > | operator+ (const slip::Vector3d< T > &val, const DenseVector3dField3d< T > &M1) |
| addition of a Vector3d to each element of a DenseVector3dField3d More... | |
| template<typename T > | |
| DenseVector3dField3d< T > | operator- (const DenseVector3dField3d< T > &M1, const DenseVector3dField3d< T > &M2) |
| pointwise substraction of two DenseVector3dField3d More... | |
| template<typename T > | |
| DenseVector3dField3d< T > | operator- (const DenseVector3dField3d< T > &M1, const slip::Vector3d< T > &val) |
| substraction of a Vector3d to each element of a DenseVector3dField3d More... | |
| template<typename T > | |
| DenseVector3dField3d< T > | operator- (const slip::Vector3d< T > &val, const DenseVector3dField3d< T > &M1) |
| substraction of a Vector3d to each element of a DenseVector3dField3d More... | |
| template<typename T > | |
| DenseVector3dField3d< T > | operator* (const DenseVector3dField3d< T > &M1, const DenseVector3dField3d< T > &M2) |
| pointwise multiplication of two DenseVector3dField3d More... | |
| template<typename T > | |
| DenseVector3dField3d< T > | operator* (const DenseVector3dField3d< T > &M1, const slip::Vector3d< T > &val) |
| multiplication of a Vector3d to each element of a DenseVector3dField3d More... | |
| template<typename T > | |
| DenseVector3dField3d< T > | operator* (const slip::Vector3d< T > &val, const DenseVector3dField3d< T > &M1) |
| multiplication of a Vector3d to each element of a DenseVector3dField3d More... | |
| template<typename T > | |
| DenseVector3dField3d< T > | operator/ (const DenseVector3dField3d< T > &M1, const DenseVector3dField3d< T > &M2) |
| pointwise division of two DenseVector3dField3d More... | |
| template<typename T > | |
| DenseVector3dField3d< T > | operator/ (const DenseVector3dField3d< T > &M1, const slip::Vector3d< T > &val) |
| division of a Vector3d to each element of a DenseVector3dField3d More... | |
Arithmetical operators | |
| template<typename T > | |
| GrayscaleImage< T > | operator+ (const GrayscaleImage< T > &M1, const GrayscaleImage< T > &M2) |
| pointwise addition of two GrayscaleImage More... | |
| template<typename T > | |
| GrayscaleImage< T > | operator+ (const GrayscaleImage< T > &M1, const T &val) |
| addition of a scalar to each element of a GrayscaleImage More... | |
| template<typename T > | |
| GrayscaleImage< T > | operator+ (const T &val, const GrayscaleImage< T > &M1) |
| addition of a scalar to each element of a GrayscaleImage More... | |
| template<typename T > | |
| GrayscaleImage< T > | operator- (const GrayscaleImage< T > &M1, const GrayscaleImage< T > &M2) |
| pointwise substraction of two GrayscaleImage More... | |
| template<typename T > | |
| GrayscaleImage< T > | operator- (const GrayscaleImage< T > &M1, const T &val) |
| substraction of a scalar to each element of a GrayscaleImage More... | |
| template<typename T > | |
| GrayscaleImage< T > | operator- (const T &val, const GrayscaleImage< T > &M1) |
| substraction of a scalar to each element of a GrayscaleImage More... | |
| template<typename T > | |
| GrayscaleImage< T > | operator* (const GrayscaleImage< T > &M1, const GrayscaleImage< T > &M2) |
| pointwise multiplication of two GrayscaleImage More... | |
| template<typename T > | |
| GrayscaleImage< T > | operator* (const GrayscaleImage< T > &M1, const T &val) |
| multiplication of a scalar to each element of a GrayscaleImage More... | |
| template<typename T > | |
| GrayscaleImage< T > | operator* (const T &val, const GrayscaleImage< T > &M1) |
| multiplication of a scalar to each element of a GrayscaleImage More... | |
| template<typename T > | |
| GrayscaleImage< T > | operator/ (const GrayscaleImage< T > &M1, const GrayscaleImage< T > &M2) |
| pointwise division of two GrayscaleImage More... | |
| template<typename T > | |
| GrayscaleImage< T > | operator/ (const GrayscaleImage< T > &M1, const T &val) |
| division of a scalar to each element of a GrayscaleImage More... | |
| template<typename T > | |
| Matrix< T > | operator+ (const Matrix< T > &M1, const Matrix< T > &M2) |
| pointwise addition of two Matrix More... | |
| template<typename T > | |
| Matrix< T > | operator+ (const Matrix< T > &M1, const T &val) |
| addition of a scalar to each element of a Matrix More... | |
| template<typename T > | |
| Matrix< T > | operator+ (const T &val, const Matrix< T > &M1) |
| addition of a scalar to each element of a Matrix More... | |
| template<typename T > | |
| Matrix< T > | operator- (const Matrix< T > &M1, const Matrix< T > &M2) |
| pointwise substraction of two Matrix More... | |
| template<typename T > | |
| Matrix< T > | operator- (const Matrix< T > &M1, const T &val) |
| substraction of a scalar to each element of a Matrix More... | |
| template<typename T > | |
| Matrix< T > | operator- (const T &val, const Matrix< T > &M1) |
| substraction of a scalar to each element of a Matrix More... | |
| template<typename T > | |
| Matrix< T > | operator* (const Matrix< T > &M1, const Matrix< T > &M2) |
| pointwise multiplication of two Matrix More... | |
| template<typename T > | |
| Matrix< T > | operator* (const Matrix< T > &M1, const T &val) |
| multiplication of a scalar to each element of a Matrix More... | |
| template<typename T > | |
| Matrix< T > | operator* (const T &val, const Matrix< T > &M1) |
| multiplication of a scalar to each element of a Matrix More... | |
| template<typename T > | |
| Matrix< T > | operator/ (const Matrix< T > &M1, const Matrix< T > &M2) |
| pointwise division of two Matrix More... | |
| template<typename T > | |
| Matrix< T > | operator/ (const Matrix< T > &M1, const T &val) |
| division of a scalar to each element of a Matrix More... | |
| template<typename T > | |
| Matrix3d< T > | operator+ (const Matrix3d< T > &M1, const Matrix3d< T > &M2) |
| pointwise addition of two Matrix3d More... | |
| template<typename T > | |
| Matrix3d< T > | operator+ (const Matrix3d< T > &M1, const T &val) |
| addition of a scalar to each element of a Matrix3d More... | |
| template<typename T > | |
| Matrix3d< T > | operator+ (const T &val, const Matrix3d< T > &M1) |
| addition of a scalar to each element of a Matrix3d More... | |
| template<typename T > | |
| Matrix3d< T > | operator- (const Matrix3d< T > &M1, const Matrix3d< T > &M2) |
| pointwise substraction of two Matrix3d More... | |
| template<typename T > | |
| Matrix3d< T > | operator- (const Matrix3d< T > &M1, const T &val) |
| substraction of a scalar to each element of a Matrix3d More... | |
| template<typename T > | |
| Matrix3d< T > | operator- (const T &val, const Matrix3d< T > &M1) |
| substraction of a scalar to each element of a Matrix3d More... | |
| template<typename T > | |
| Matrix3d< T > | operator* (const Matrix3d< T > &M1, const Matrix3d< T > &M2) |
| pointwise multiplication of two Matrix3d More... | |
| template<typename T > | |
| Matrix3d< T > | operator* (const Matrix3d< T > &M1, const T &val) |
| multiplication of a scalar to each element of a Matrix3d More... | |
| template<typename T > | |
| Matrix3d< T > | operator* (const T &val, const Matrix3d< T > &M1) |
| multiplication of a scalar to each element of a Matrix3d More... | |
| template<typename T > | |
| Matrix3d< T > | operator/ (const Matrix3d< T > &M1, const Matrix3d< T > &M2) |
| pointwise division of two Matrix3d More... | |
| template<typename T > | |
| Matrix3d< T > | operator/ (const Matrix3d< T > &M1, const T &val) |
| division of a scalar to each element of a Matrix3d More... | |
| template<typename T > | |
| Matrix4d< T > | operator+ (const Matrix4d< T > &M1, const Matrix4d< T > &M2) |
| pointwise addition of two Matrix4d More... | |
| template<typename T > | |
| Matrix4d< T > | operator+ (const Matrix4d< T > &M1, const T &val) |
| addition of a scalar to each element of a Matrix4d More... | |
| template<typename T > | |
| Matrix4d< T > | operator+ (const T &val, const Matrix4d< T > &M1) |
| addition of a scalar to each element of a Matrix4d More... | |
| template<typename T > | |
| Matrix4d< T > | operator- (const Matrix4d< T > &M1, const Matrix4d< T > &M2) |
| pointwise substraction of two Matrix4d More... | |
| template<typename T > | |
| Matrix4d< T > | operator- (const Matrix4d< T > &M1, const T &val) |
| substraction of a scalar to each element of a Matrix4d More... | |
| template<typename T > | |
| Matrix4d< T > | operator- (const T &val, const Matrix4d< T > &M1) |
| substraction of a scalar to each element of a Matrix4d More... | |
| template<typename T > | |
| Matrix4d< T > | operator* (const Matrix4d< T > &M1, const Matrix4d< T > &M2) |
| pointwise multiplication of two Matrix4d More... | |
| template<typename T > | |
| Matrix4d< T > | operator* (const Matrix4d< T > &M1, const T &val) |
| multiplication of a scalar to each element of a Matrix4d More... | |
| template<typename T > | |
| Matrix4d< T > | operator* (const T &val, const Matrix4d< T > &M1) |
| multiplication of a scalar to each element of a Matrix4d More... | |
| template<typename T > | |
| Matrix4d< T > | operator/ (const Matrix4d< T > &M1, const Matrix4d< T > &M2) |
| pointwise division of two Matrix4d More... | |
| template<typename T > | |
| Matrix4d< T > | operator/ (const Matrix4d< T > &M1, const T &val) |
| division of a scalar to each element of a Matrix4d More... | |
i/o operators | |
| template<typename T > | |
| std::ostream & | operator<< (std::ostream &out, const slip::Matrix3d< T > &a) |
| template<typename T > | |
| std::ostream & | operator<< (std::ostream &out, const slip::Matrix4d< T > &a) |
EqualityComparable operators | |
| template<typename T > | |
| bool | operator== (const slip::Matrix3d< T > &x, const slip::Matrix3d< T > &y) |
| template<typename T > | |
| bool | operator!= (const slip::Matrix3d< T > &x, const slip::Matrix3d< T > &y) |
| template<typename T > | |
| bool | operator== (const slip::Matrix4d< T > &x, const slip::Matrix4d< T > &y) |
| template<typename T > | |
| bool | operator!= (const slip::Matrix4d< T > &x, const slip::Matrix4d< T > &y) |
LessThanComparable operators | |
| template<typename T > | |
| bool | operator< (const slip::Matrix3d< T > &x, const slip::Matrix3d< T > &y) |
| template<typename T > | |
| bool | operator> (const slip::Matrix3d< T > &x, const slip::Matrix3d< T > &y) |
| template<typename T > | |
| bool | operator<= (const slip::Matrix3d< T > &x, const slip::Matrix3d< T > &y) |
| template<typename T > | |
| bool | operator>= (const slip::Matrix3d< T > &x, const slip::Matrix3d< T > &y) |
| template<typename T > | |
| bool | operator< (const slip::Matrix4d< T > &x, const slip::Matrix4d< T > &y) |
| template<typename T > | |
| bool | operator> (const slip::Matrix4d< T > &x, const slip::Matrix4d< T > &y) |
| template<typename T > | |
| bool | operator<= (const slip::Matrix4d< T > &x, const slip::Matrix4d< T > &y) |
| template<typename T > | |
| bool | operator>= (const slip::Matrix4d< T > &x, const slip::Matrix4d< T > &y) |
LessThan functions | |
| template<std::size_t DIM> | |
| bool | operator< (const Monomial< DIM > &x, const Monomial< DIM > &y) |
| template<std::size_t DIM> | |
| bool | operator> (const Monomial< DIM > &x, const Monomial< DIM > &y) |
Arithmetic operators | |
| template<std::size_t DIM> | |
| Monomial< DIM > | operator* (const Monomial< DIM > &monomial1, const Monomial< DIM > &monomial2) |
| Monomial multiplication. More... | |
Arithemtical operators | |
Arithmetical functions | |
| template<typename T > | |
| Signal< T > | operator+ (const Signal< T > &V1, const Signal< T > &V2) |
| pointwise addition of two Signal More... | |
| template<typename T > | |
| Signal< T > | operator+ (const Signal< T > &V, const T &val) |
| addition of a scalar to each element of a Signal More... | |
| template<typename T > | |
| Signal< T > | operator+ (const T &val, const Signal< T > &V) |
| addition of a scalar to each element of a Signal More... | |
| template<typename T > | |
| Signal< T > | operator- (const Signal< T > &V1, const Signal< T > &V2) |
| pointwise substraction of two Signal More... | |
| template<typename T > | |
| Signal< T > | operator- (const Signal< T > &V, const T &val) |
| substraction of a scalar to each element of a Signal More... | |
| template<typename T > | |
| Signal< T > | operator- (const T &val, const Signal< T > &V) |
| substraction of a scalar to each element of a Signal More... | |
| template<typename T > | |
| Signal< T > | operator* (const Signal< T > &V1, const Signal< T > &V2) |
| pointwise multiplication of two Signal More... | |
| template<typename T > | |
| Signal< T > | operator* (const Signal< T > &V, const T &val) |
| multiplication of a scalar to each element of a Signal More... | |
| template<typename T > | |
| Signal< T > | operator* (const T &val, const Signal< T > &V) |
| multiplication of a scalar to each element of a Signal More... | |
| template<typename T > | |
| Signal< T > | operator/ (const Signal< T > &V1, const Signal< T > &V2) |
| pointwise division of two Signal More... | |
| template<typename T > | |
| Signal< T > | operator/ (const Signal< T > &V, const T &val) |
| division of a scalar to each element of a Signal More... | |
| template<typename T > | |
| Vector< T > | operator+ (const Vector< T > &V1, const Vector< T > &V2) |
| pointwise addition of two Vector More... | |
| template<typename T > | |
| Vector< T > | operator+ (const Vector< T > &V, const T &val) |
| addition of a scalar to each element of a Vector More... | |
| template<typename T > | |
| Vector< T > | operator+ (const T &val, const Vector< T > &V) |
| addition of a scalar to each element of a Vector More... | |
| template<typename T > | |
| Vector< T > | operator- (const Vector< T > &V1, const Vector< T > &V2) |
| pointwise substraction of two Vector More... | |
| template<typename T > | |
| Vector< T > | operator- (const Vector< T > &V, const T &val) |
| substraction of a scalar to each element of a Vector More... | |
| template<typename T > | |
| Vector< T > | operator- (const T &val, const Vector< T > &V) |
| substraction of a scalar to each element of a Vector More... | |
| template<typename T > | |
| Vector< T > | operator* (const Vector< T > &V1, const Vector< T > &V2) |
| pointwise multiplication of two Vector More... | |
| template<typename T > | |
| Vector< T > | operator* (const Vector< T > &V, const T &val) |
| multiplication of a scalar to each element of a Vector More... | |
| template<typename T > | |
| Vector< T > | operator* (const T &val, const Vector< T > &V) |
| multiplication of a scalar to each element of a Vector More... | |
| template<typename T > | |
| Vector< T > | operator/ (const Vector< T > &V1, const Vector< T > &V2) |
| pointwise division of two Vector More... | |
| template<typename T > | |
| Vector< T > | operator/ (const Vector< T > &V, const T &val) |
| division of a scalar to each element of a Vector More... | |
input/output functions | |
| template<typename T > | |
| std::ostream & | operator<< (std::ostream &out, const slip::Volume< T > &a) |
Variables | |
| const std::string | FILE_OPEN_ERROR = "Fail to open file: " |
| const std::string | CROSSCORRELATION_BAD_ALGO = "Bad crosscorrelation algorithm selection: standard algorithm by default" |
| const std::string | SINGULAR_MATRIX_ERROR = "This matrix is singular" |
| const std::string | POSITIVE_DEFINITE_MATRIX_ERROR = "This matrix is not positive definite" |
| const std::string | GRID_INIT_POINT_ERROR = "The init points of the grid are different" |
| const std::string | GRID_STEP_ERROR = "The grid steps of the grid are different" |
| const std::string | FILE_READ_ERROR = "Unable to read the file " |
| const std::string | FILE_WRITE_ERROR = "Unable to write into the file " |
| const std::string | BAD_DIMENSION = "Bad dimension parameter." |
| const std::string | BAD_PARAMETER = "Bad parameter." |
Some useful 1d-neighborhood configurations | |
Some useful 2d-neighborhood configurations | |
Some useful 3d-neighborhood configurations | |
Some useful 4d-neighborhood configurations | |
Derivatives algorithms | |
| enum | FOUR_DIM_DIRECTION { T_DIRECTION, S_DIRECTION, R_DIRECTION, C_DIRECTION } |
| Choose between different directions in a 4D space. More... | |
| template<class Container2D > | |
| void | finite_diff_coef (const std::size_t sch_ord, const std::size_t sch_shift, Container2D &Dinv) |
| return finite differences coefficients for derivation based on Taylor series (sch_ord-sch_shift steps upwind). More... | |
| template<class Container2D > | |
| void | finite_diff_coef (const std::size_t sch_ord, const std::size_t sch_shift, const typename Container2D::value_type &h, Container2D &Dinv) |
| return finite differences coefficients for derivation based on Taylor series (sch_ord-sch_shift steps upwind) More... | |
| template<typename KernelsIterator > | |
| void | finite_diff_kernels (const std::size_t der_ord, const std::size_t sch_ord, const std::size_t sch_shift, std::vector< KernelsIterator > &kernels_first) |
| Computes finite differences kernels for derivation based on Taylor series (sch_ord-sch_shift steps upwind) More... | |
| template<typename KernelsIterator > | |
| void | finite_diff_kernels (const std::size_t der_ord, const std::size_t sch_ord, const std::size_t sch_shift, const typename std::iterator_traits< KernelsIterator >::value_type &h, std::vector< KernelsIterator > &kernels_first) |
| Computes finite differences kernels for derivation based on Taylor series (sch_ord-sch_shift steps upwind) More... | |
| template<typename SrcIter , typename Container2D , typename ResIter > | |
| void | derivative (SrcIter first, SrcIter last, const std::size_t der_ord, const std::size_t sch_ord, const std::size_t sch_shift, const Container2D &M, ResIter result) |
| Computes 1d finite differences derivatives of an iterator range. More... | |
| template<typename SrcIter , typename KernelsIterator , typename ResIter > | |
| void | derivative (SrcIter first, SrcIter last, const std::size_t der_ord, const std::size_t sch_ord, const std::size_t sch_shift, const std::vector< KernelsIterator > &kernels_first, ResIter result) |
| Computes 1d finite differences derivatives of an iterator range. More... | |
| template<typename Iterator2d1 , typename Iterator2d2 , typename T > | |
| void | derivative_2d (Iterator2d1 I_up, Iterator2d1 I_bot, const slip::Point2d< T > &grid_step, slip::SPATIAL_DIRECTION der_dir, const std::size_t der_order, const std::size_t sch_order, Iterator2d2 R_up, Iterator2d2 R_bot) |
| Computes finite differences derivatives of a 2d range. More... | |
| template<typename RandomAccessIterator3d1 , typename RandomAccessIterator3d2 , typename T > | |
| void | derivative_3d (RandomAccessIterator3d1 I_fup, RandomAccessIterator3d1 I_back_bot, const slip::Point3d< T > &grid_step, slip::SPATIAL_DIRECTION der_dir, const std::size_t der_order, const std::size_t sch_order, RandomAccessIterator3d2 R_fup, RandomAccessIterator3d2 R_back_bot) |
| Computes finite differences derivatives of a 3d range. More... | |
| template<typename RandomAccessIterator4d1 , typename RandomAccessIterator4d2 , typename T > | |
| void | derivative_4d (RandomAccessIterator4d1 I_ffup, RandomAccessIterator4d1 I_last_back_bot, const slip::Point4d< T > &grid_step, slip::FOUR_DIM_DIRECTION der_dir, const std::size_t der_order, const std::size_t sch_order, RandomAccessIterator4d2 R_ffup, RandomAccessIterator4d2 R_last_back_bot) |
| Computes finite differences derivatives of a 4d range. More... | |
This namespace corresponds to the kernel of the Simple Library on Image Processing (SLIP). That is to say that it contains the data structures and the algorithms needed by these data strucutres.
namespace slip
| typedef slip::Array2d<char> slip::Array2d_c |
char alias
Definition at line 2242 of file Array2d.hpp.
| typedef slip::Array2d<double> slip::Array2d_d |
double alias
Definition at line 2226 of file Array2d.hpp.
| typedef slip::Array2d<float> slip::Array2d_f |
float alias
Definition at line 2228 of file Array2d.hpp.
| typedef slip::Array2d<int> slip::Array2d_i |
int alias
Definition at line 2238 of file Array2d.hpp.
| typedef slip::Array2d<long> slip::Array2d_l |
long alias
Definition at line 2230 of file Array2d.hpp.
| typedef slip::Array2d<short> slip::Array2d_s |
short alias
Definition at line 2234 of file Array2d.hpp.
| typedef slip::Array2d<unsigned char> slip::Array2d_uc |
unsigned char alias
Definition at line 2244 of file Array2d.hpp.
| typedef slip::Array2d<unsigned int> slip::Array2d_ui |
unsigned int alias
Definition at line 2240 of file Array2d.hpp.
| typedef slip::Array2d<unsigned long> slip::Array2d_ul |
unsigned long alias
Definition at line 2232 of file Array2d.hpp.
| typedef slip::Array2d<unsigned short> slip::Array2d_us |
unsigned long alias
Definition at line 2236 of file Array2d.hpp.
| typedef slip::Array3d<char> slip::Array3d_c |
char alias
Definition at line 3495 of file Array3d.hpp.
| typedef slip::Array3d<double> slip::Array3d_d |
double alias
Definition at line 3479 of file Array3d.hpp.
| typedef slip::Array3d<float> slip::Array3d_f |
float alias
Definition at line 3481 of file Array3d.hpp.
| typedef slip::Array3d<int> slip::Array3d_i |
int alias
Definition at line 3491 of file Array3d.hpp.
| typedef slip::Array3d<long> slip::Array3d_l |
long alias
Definition at line 3483 of file Array3d.hpp.
| typedef slip::Array3d<short> slip::Array3d_s |
short alias
Definition at line 3487 of file Array3d.hpp.
| typedef slip::Array3d<unsigned char> slip::Array3d_uc |
unsigned char alias
Definition at line 3497 of file Array3d.hpp.
| typedef slip::Array3d<unsigned int> slip::Array3d_ui |
unsigned int alias
Definition at line 3493 of file Array3d.hpp.
| typedef slip::Array3d<unsigned long> slip::Array3d_ul |
unsigned long alias
Definition at line 3485 of file Array3d.hpp.
| typedef slip::Array3d<unsigned short> slip::Array3d_us |
unsigned long alias
Definition at line 3489 of file Array3d.hpp.
| typedef slip::Array4d<char> slip::Array4d_c |
char alias
Definition at line 3237 of file Array4d.hpp.
| typedef slip::Array4d<double> slip::Array4d_d |
double alias
Definition at line 3221 of file Array4d.hpp.
| typedef slip::Array4d<float> slip::Array4d_f |
float alias
Definition at line 3223 of file Array4d.hpp.
| typedef slip::Array4d<int> slip::Array4d_i |
int alias
Definition at line 3233 of file Array4d.hpp.
| typedef slip::Array4d<long> slip::Array4d_l |
long alias
Definition at line 3225 of file Array4d.hpp.
| typedef slip::Array4d<short> slip::Array4d_s |
short alias
Definition at line 3229 of file Array4d.hpp.
| typedef slip::Array4d<unsigned char> slip::Array4d_uc |
unsigned char alias
Definition at line 3239 of file Array4d.hpp.
| typedef slip::Array4d<unsigned int> slip::Array4d_ui |
unsigned int alias
Definition at line 3235 of file Array4d.hpp.
| typedef slip::Array4d<unsigned long> slip::Array4d_ul |
unsigned long alias
Definition at line 3227 of file Array4d.hpp.
| typedef slip::Array4d<unsigned short> slip::Array4d_us |
unsigned long alias
Definition at line 3231 of file Array4d.hpp.
| typedef slip::Array<char> slip::Array_c |
| typedef slip::Array<double> slip::Array_d |
| typedef slip::Array<float> slip::Array_f |
| typedef slip::Array<int> slip::Array_i |
| typedef slip::Array<long> slip::Array_l |
| typedef slip::Array<short> slip::Array_s |
| typedef slip::Array<unsigned char> slip::Array_uc |
| typedef slip::Array<unsigned int> slip::Array_ui |
| typedef slip::Array<unsigned long> slip::Array_ul |
| typedef slip::Array<unsigned short> slip::Array_us |
| typedef slip::Color<char> slip::Color_c |
| typedef slip::Color<double> slip::Color_d |
| typedef slip::Color<float> slip::Color_f |
| typedef slip::Color<int> slip::Color_i |
| typedef slip::Color<long> slip::Color_l |
| typedef slip::Color<short> slip::Color_s |
| typedef slip::Color<unsigned char> slip::Color_uc |
| typedef slip::Color<unsigned int> slip::Color_ui |
| typedef slip::Color<unsigned long> slip::Color_ul |
| typedef slip::Color<unsigned short> slip::Color_us |
| typedef slip::ColorHyperVolume<char> slip::ColorHyperVolume_c |
char alias
Definition at line 368 of file ColorHyperVolume.hpp.
| typedef slip::ColorHyperVolume<double> slip::ColorHyperVolume_d |
double alias
Definition at line 352 of file ColorHyperVolume.hpp.
| typedef slip::ColorHyperVolume<float> slip::ColorHyperVolume_f |
float alias
Definition at line 354 of file ColorHyperVolume.hpp.
| typedef slip::ColorHyperVolume<int> slip::ColorHyperVolume_i |
int alias
Definition at line 364 of file ColorHyperVolume.hpp.
| typedef slip::ColorHyperVolume<long> slip::ColorHyperVolume_l |
long alias
Definition at line 356 of file ColorHyperVolume.hpp.
| typedef slip::ColorHyperVolume<short> slip::ColorHyperVolume_s |
short alias
Definition at line 360 of file ColorHyperVolume.hpp.
| typedef slip::ColorHyperVolume<unsigned char> slip::ColorHyperVolume_uc |
unsigned char alias
Definition at line 370 of file ColorHyperVolume.hpp.
| typedef slip::ColorHyperVolume<unsigned int> slip::ColorHyperVolume_ui |
unsigned int alias
Definition at line 366 of file ColorHyperVolume.hpp.
| typedef slip::ColorHyperVolume<unsigned long> slip::ColorHyperVolume_ul |
unsigned long alias
Definition at line 358 of file ColorHyperVolume.hpp.
| typedef slip::ColorHyperVolume<unsigned short> slip::ColorHyperVolume_us |
unsigned long alias
Definition at line 362 of file ColorHyperVolume.hpp.
| typedef slip::ColorImage<char> slip::ColorImage_c |
char alias
Definition at line 487 of file ColorImage.hpp.
| typedef slip::ColorImage<double> slip::ColorImage_d |
double alias
Definition at line 471 of file ColorImage.hpp.
| typedef slip::ColorImage<float> slip::ColorImage_f |
float alias
Definition at line 473 of file ColorImage.hpp.
| typedef slip::ColorImage<int> slip::ColorImage_i |
int alias
Definition at line 483 of file ColorImage.hpp.
| typedef slip::ColorImage<long> slip::ColorImage_l |
long alias
Definition at line 475 of file ColorImage.hpp.
| typedef slip::ColorImage<short> slip::ColorImage_s |
short alias
Definition at line 479 of file ColorImage.hpp.
| typedef slip::ColorImage<unsigned char> slip::ColorImage_uc |
unsigned char alias
Definition at line 489 of file ColorImage.hpp.
| typedef slip::ColorImage<unsigned int> slip::ColorImage_ui |
unsigned int alias
Definition at line 485 of file ColorImage.hpp.
| typedef slip::ColorImage<unsigned long> slip::ColorImage_ul |
unsigned long alias
Definition at line 477 of file ColorImage.hpp.
| typedef slip::ColorImage<unsigned short> slip::ColorImage_us |
unsigned long alias
Definition at line 481 of file ColorImage.hpp.
| typedef slip::Colormap<char> slip::Colormap_c |
char alias
Definition at line 721 of file Colormap.hpp.
| typedef slip::Colormap<double> slip::Colormap_d |
double alias
Definition at line 705 of file Colormap.hpp.
| typedef slip::Colormap<float> slip::Colormap_f |
float alias
Definition at line 707 of file Colormap.hpp.
| typedef slip::Colormap<int> slip::Colormap_i |
int alias
Definition at line 717 of file Colormap.hpp.
| typedef slip::Colormap<long> slip::Colormap_l |
long alias
Definition at line 709 of file Colormap.hpp.
| typedef slip::Colormap<short> slip::Colormap_s |
short alias
Definition at line 713 of file Colormap.hpp.
| typedef slip::Colormap<unsigned char> slip::Colormap_uc |
unsigned char alias
Definition at line 723 of file Colormap.hpp.
| typedef slip::Colormap<unsigned int> slip::Colormap_ui |
unsigned int alias
Definition at line 719 of file Colormap.hpp.
| typedef slip::Colormap<unsigned long> slip::Colormap_ul |
unsigned long alias
Definition at line 711 of file Colormap.hpp.
| typedef slip::Colormap<unsigned short> slip::Colormap_us |
unsigned long alias
Definition at line 715 of file Colormap.hpp.
| typedef slip::DenseVector2dField2d<char> slip::DenseVector2dField2d_c |
char alias
Definition at line 734 of file DenseVector2dField2d.hpp.
| typedef slip::DenseVector2dField2d<double> slip::DenseVector2dField2d_d |
double alias
Definition at line 718 of file DenseVector2dField2d.hpp.
| typedef slip::DenseVector2dField2d<float> slip::DenseVector2dField2d_f |
float alias
Definition at line 720 of file DenseVector2dField2d.hpp.
| typedef slip::DenseVector2dField2d<int> slip::DenseVector2dField2d_i |
int alias
Definition at line 730 of file DenseVector2dField2d.hpp.
| typedef slip::DenseVector2dField2d<long> slip::DenseVector2dField2d_l |
long alias
Definition at line 722 of file DenseVector2dField2d.hpp.
| typedef slip::DenseVector2dField2d<short> slip::DenseVector2dField2d_s |
short alias
Definition at line 726 of file DenseVector2dField2d.hpp.
| typedef slip::DenseVector2dField2d<unsigned char> slip::DenseVector2dField2d_uc |
unsigned char alias
Definition at line 736 of file DenseVector2dField2d.hpp.
| typedef slip::DenseVector2dField2d<unsigned int> slip::DenseVector2dField2d_ui |
unsigned int alias
Definition at line 732 of file DenseVector2dField2d.hpp.
| typedef slip::DenseVector2dField2d<unsigned long> slip::DenseVector2dField2d_ul |
unsigned long alias
Definition at line 724 of file DenseVector2dField2d.hpp.
| typedef slip::DenseVector2dField2d<unsigned short> slip::DenseVector2dField2d_us |
unsigned long alias
Definition at line 728 of file DenseVector2dField2d.hpp.
| typedef slip::DenseVector3dField2d<char> slip::DenseVector3dField2d_c |
char alias
Definition at line 573 of file DenseVector3dField2d.hpp.
| typedef slip::DenseVector3dField2d<double> slip::DenseVector3dField2d_d |
double alias
Definition at line 557 of file DenseVector3dField2d.hpp.
| typedef slip::DenseVector3dField2d<float> slip::DenseVector3dField2d_f |
float alias
Definition at line 559 of file DenseVector3dField2d.hpp.
| typedef slip::DenseVector3dField2d<int> slip::DenseVector3dField2d_i |
int alias
Definition at line 569 of file DenseVector3dField2d.hpp.
| typedef slip::DenseVector3dField2d<long> slip::DenseVector3dField2d_l |
long alias
Definition at line 561 of file DenseVector3dField2d.hpp.
| typedef slip::DenseVector3dField2d<short> slip::DenseVector3dField2d_s |
short alias
Definition at line 565 of file DenseVector3dField2d.hpp.
| typedef slip::DenseVector3dField2d<unsigned char> slip::DenseVector3dField2d_uc |
unsigned char alias
Definition at line 575 of file DenseVector3dField2d.hpp.
| typedef slip::DenseVector3dField2d<unsigned int> slip::DenseVector3dField2d_ui |
unsigned int alias
Definition at line 571 of file DenseVector3dField2d.hpp.
| typedef slip::DenseVector3dField2d<unsigned long> slip::DenseVector3dField2d_ul |
unsigned long alias
Definition at line 563 of file DenseVector3dField2d.hpp.
| typedef slip::DenseVector3dField2d<unsigned short> slip::DenseVector3dField2d_us |
unsigned long alias
Definition at line 567 of file DenseVector3dField2d.hpp.
| typedef slip::DenseVector3dField3d<char> slip::DenseVector3dField3d_c |
char alias
Definition at line 794 of file DenseVector3dField3d.hpp.
| typedef slip::DenseVector3dField3d<double> slip::DenseVector3dField3d_d |
double alias
Definition at line 778 of file DenseVector3dField3d.hpp.
| typedef slip::DenseVector3dField3d<float> slip::DenseVector3dField3d_f |
float alias
Definition at line 780 of file DenseVector3dField3d.hpp.
| typedef slip::DenseVector3dField3d<int> slip::DenseVector3dField3d_i |
int alias
Definition at line 790 of file DenseVector3dField3d.hpp.
| typedef slip::DenseVector3dField3d<long> slip::DenseVector3dField3d_l |
long alias
Definition at line 782 of file DenseVector3dField3d.hpp.
| typedef slip::DenseVector3dField3d<short> slip::DenseVector3dField3d_s |
short alias
Definition at line 786 of file DenseVector3dField3d.hpp.
| typedef slip::DenseVector3dField3d<unsigned char> slip::DenseVector3dField3d_uc |
unsigned char alias
Definition at line 796 of file DenseVector3dField3d.hpp.
| typedef slip::DenseVector3dField3d<unsigned int> slip::DenseVector3dField3d_ui |
unsigned int alias
Definition at line 792 of file DenseVector3dField3d.hpp.
| typedef slip::DenseVector3dField3d<unsigned long> slip::DenseVector3dField3d_ul |
unsigned long alias
Definition at line 784 of file DenseVector3dField3d.hpp.
| typedef slip::DenseVector3dField3d<unsigned short> slip::DenseVector3dField3d_us |
unsigned long alias
Definition at line 788 of file DenseVector3dField3d.hpp.
| typedef slip::GrayscaleImage<char> slip::GrayscaleImage_c |
char alias
Definition at line 2354 of file GrayscaleImage.hpp.
| typedef slip::GrayscaleImage<double> slip::GrayscaleImage_d |
double alias
Definition at line 2338 of file GrayscaleImage.hpp.
| typedef slip::GrayscaleImage<float> slip::GrayscaleImage_f |
float alias
Definition at line 2340 of file GrayscaleImage.hpp.
| typedef slip::GrayscaleImage<int> slip::GrayscaleImage_i |
int alias
Definition at line 2350 of file GrayscaleImage.hpp.
| typedef slip::GrayscaleImage<long> slip::GrayscaleImage_l |
long alias
Definition at line 2342 of file GrayscaleImage.hpp.
| typedef slip::GrayscaleImage<short> slip::GrayscaleImage_s |
short alias
Definition at line 2346 of file GrayscaleImage.hpp.
| typedef slip::GrayscaleImage<unsigned char> slip::GrayscaleImage_uc |
unsigned char alias
Definition at line 2356 of file GrayscaleImage.hpp.
| typedef slip::GrayscaleImage<unsigned int> slip::GrayscaleImage_ui |
unsigned int alias
Definition at line 2352 of file GrayscaleImage.hpp.
| typedef slip::GrayscaleImage<unsigned long> slip::GrayscaleImage_ul |
unsigned long alias
Definition at line 2344 of file GrayscaleImage.hpp.
| typedef slip::GrayscaleImage<unsigned short> slip::GrayscaleImage_us |
unsigned long alias
Definition at line 2348 of file GrayscaleImage.hpp.
| typedef slip::HyperVolume<char> slip::HyperVolume_c |
char alias
Definition at line 3268 of file HyperVolume.hpp.
| typedef slip::HyperVolume<double> slip::HyperVolume_d |
double alias
Definition at line 3252 of file HyperVolume.hpp.
| typedef slip::HyperVolume<float> slip::HyperVolume_f |
float alias
Definition at line 3254 of file HyperVolume.hpp.
| typedef slip::HyperVolume<int> slip::HyperVolume_i |
int alias
Definition at line 3264 of file HyperVolume.hpp.
| typedef slip::HyperVolume<long> slip::HyperVolume_l |
long alias
Definition at line 3256 of file HyperVolume.hpp.
| typedef slip::HyperVolume<short> slip::HyperVolume_s |
short alias
Definition at line 3260 of file HyperVolume.hpp.
| typedef slip::HyperVolume<unsigned char> slip::HyperVolume_uc |
unsigned char alias
Definition at line 3270 of file HyperVolume.hpp.
| typedef slip::HyperVolume<unsigned int> slip::HyperVolume_ui |
unsigned int alias
Definition at line 3266 of file HyperVolume.hpp.
| typedef slip::HyperVolume<unsigned long> slip::HyperVolume_ul |
unsigned long alias
Definition at line 3258 of file HyperVolume.hpp.
| typedef slip::HyperVolume<unsigned short> slip::HyperVolume_us |
unsigned long alias
Definition at line 3262 of file HyperVolume.hpp.
| typedef slip::Matrix3d<char> slip::Matrix3d_c |
char alias
Definition at line 3558 of file Matrix3d.hpp.
| typedef slip::Matrix3d<double> slip::Matrix3d_d |
double alias
Definition at line 3542 of file Matrix3d.hpp.
| typedef slip::Matrix3d<float> slip::Matrix3d_f |
float alias
Definition at line 3544 of file Matrix3d.hpp.
| typedef slip::Matrix3d<int> slip::Matrix3d_i |
int alias
Definition at line 3554 of file Matrix3d.hpp.
| typedef slip::Matrix3d<long> slip::Matrix3d_l |
long alias
Definition at line 3546 of file Matrix3d.hpp.
| typedef slip::Matrix3d<short> slip::Matrix3d_s |
short alias
Definition at line 3550 of file Matrix3d.hpp.
| typedef slip::Matrix3d<unsigned char> slip::Matrix3d_uc |
unsigned char alias
Definition at line 3560 of file Matrix3d.hpp.
| typedef slip::Matrix3d<unsigned int> slip::Matrix3d_ui |
unsigned int alias
Definition at line 3556 of file Matrix3d.hpp.
| typedef slip::Matrix3d<unsigned long> slip::Matrix3d_ul |
unsigned long alias
Definition at line 3548 of file Matrix3d.hpp.
| typedef slip::Matrix3d<unsigned short> slip::Matrix3d_us |
unsigned long alias
Definition at line 3552 of file Matrix3d.hpp.
| typedef slip::Matrix4d<char> slip::Matrix4d_c |
char alias
Definition at line 3276 of file Matrix4d.hpp.
| typedef slip::Matrix4d<double> slip::Matrix4d_d |
double alias
Definition at line 3260 of file Matrix4d.hpp.
| typedef slip::Matrix4d<float> slip::Matrix4d_f |
float alias
Definition at line 3262 of file Matrix4d.hpp.
| typedef slip::Matrix4d<int> slip::Matrix4d_i |
int alias
Definition at line 3272 of file Matrix4d.hpp.
| typedef slip::Matrix4d<long> slip::Matrix4d_l |
long alias
Definition at line 3264 of file Matrix4d.hpp.
| typedef slip::Matrix4d<short> slip::Matrix4d_s |
short alias
Definition at line 3268 of file Matrix4d.hpp.
| typedef slip::Matrix4d<unsigned char> slip::Matrix4d_uc |
unsigned char alias
Definition at line 3278 of file Matrix4d.hpp.
| typedef slip::Matrix4d<unsigned int> slip::Matrix4d_ui |
unsigned int alias
Definition at line 3274 of file Matrix4d.hpp.
| typedef slip::Matrix4d<unsigned long> slip::Matrix4d_ul |
unsigned long alias
Definition at line 3266 of file Matrix4d.hpp.
| typedef slip::Matrix4d<unsigned short> slip::Matrix4d_us |
unsigned long alias
Definition at line 3270 of file Matrix4d.hpp.
| typedef slip::Matrix<char> slip::Matrix_c |
char alias
Definition at line 2393 of file Matrix.hpp.
| typedef slip::Matrix<double> slip::Matrix_d |
double alias
Definition at line 2377 of file Matrix.hpp.
| typedef slip::Matrix<float> slip::Matrix_f |
float alias
Definition at line 2379 of file Matrix.hpp.
| typedef slip::Matrix<int> slip::Matrix_i |
int alias
Definition at line 2389 of file Matrix.hpp.
| typedef slip::Matrix<long> slip::Matrix_l |
long alias
Definition at line 2381 of file Matrix.hpp.
| typedef slip::Matrix<short> slip::Matrix_s |
short alias
Definition at line 2385 of file Matrix.hpp.
| typedef slip::Matrix<unsigned char> slip::Matrix_uc |
unsigned char alias
Definition at line 2395 of file Matrix.hpp.
| typedef slip::Matrix<unsigned int> slip::Matrix_ui |
unsigned int alias
Definition at line 2391 of file Matrix.hpp.
| typedef slip::Matrix<unsigned long> slip::Matrix_ul |
unsigned long alias
Definition at line 2383 of file Matrix.hpp.
| typedef slip::Matrix<unsigned short> slip::Matrix_us |
unsigned long alias
Definition at line 2387 of file Matrix.hpp.
| typedef slip::Point1d<char> slip::Point1d_c |
char alias
Definition at line 186 of file Point1d.hpp.
| typedef slip::Point1d<double> slip::Point1d_d |
double alias
Definition at line 170 of file Point1d.hpp.
| typedef slip::Point1d<float> slip::Point1d_f |
float alias
Definition at line 172 of file Point1d.hpp.
| typedef slip::Point1d<int> slip::Point1d_i |
int alias
Definition at line 182 of file Point1d.hpp.
| typedef slip::Point1d<long> slip::Point1d_l |
long alias
Definition at line 174 of file Point1d.hpp.
| typedef slip::Point1d<short> slip::Point1d_s |
short alias
Definition at line 178 of file Point1d.hpp.
| typedef slip::Point1d<unsigned char> slip::Point1d_uc |
unsigned char alias
Definition at line 188 of file Point1d.hpp.
| typedef slip::Point1d<unsigned int> slip::Point1d_ui |
unsigned int alias
Definition at line 184 of file Point1d.hpp.
| typedef slip::Point1d<unsigned long> slip::Point1d_ul |
unsigned long alias
Definition at line 176 of file Point1d.hpp.
| typedef slip::Point1d<unsigned short> slip::Point1d_us |
unsigned long alias
Definition at line 180 of file Point1d.hpp.
| typedef slip::Point2d<char> slip::Point2d_c |
char alias
Definition at line 218 of file Point2d.hpp.
| typedef slip::Point2d<double> slip::Point2d_d |
double alias
Definition at line 202 of file Point2d.hpp.
| typedef slip::Point2d<float> slip::Point2d_f |
float alias
Definition at line 204 of file Point2d.hpp.
| typedef slip::Point2d<int> slip::Point2d_i |
int alias
Definition at line 214 of file Point2d.hpp.
| typedef slip::Point2d<long> slip::Point2d_l |
long alias
Definition at line 206 of file Point2d.hpp.
| typedef slip::Point2d<short> slip::Point2d_s |
short alias
Definition at line 210 of file Point2d.hpp.
| typedef slip::Point2d<unsigned char> slip::Point2d_uc |
unsigned char alias
Definition at line 220 of file Point2d.hpp.
| typedef slip::Point2d<unsigned int> slip::Point2d_ui |
unsigned int alias
Definition at line 216 of file Point2d.hpp.
| typedef slip::Point2d<unsigned long> slip::Point2d_ul |
unsigned long alias
Definition at line 208 of file Point2d.hpp.
| typedef slip::Point2d<unsigned short> slip::Point2d_us |
unsigned long alias
Definition at line 212 of file Point2d.hpp.
| typedef slip::Point3d<char> slip::Point3d_c |
char alias
Definition at line 224 of file Point3d.hpp.
| typedef slip::Point3d<double> slip::Point3d_d |
double alias
Definition at line 208 of file Point3d.hpp.
| typedef slip::Point3d<float> slip::Point3d_f |
float alias
Definition at line 210 of file Point3d.hpp.
| typedef slip::Point3d<int> slip::Point3d_i |
int alias
Definition at line 220 of file Point3d.hpp.
| typedef slip::Point3d<long> slip::Point3d_l |
long alias
Definition at line 212 of file Point3d.hpp.
| typedef slip::Point3d<short> slip::Point3d_s |
short alias
Definition at line 216 of file Point3d.hpp.
| typedef slip::Point3d<unsigned char> slip::Point3d_uc |
unsigned char alias
Definition at line 226 of file Point3d.hpp.
| typedef slip::Point3d<unsigned int> slip::Point3d_ui |
unsigned int alias
Definition at line 222 of file Point3d.hpp.
| typedef slip::Point3d<unsigned long> slip::Point3d_ul |
unsigned long alias
Definition at line 214 of file Point3d.hpp.
| typedef slip::Point3d<unsigned short> slip::Point3d_us |
unsigned long alias
Definition at line 218 of file Point3d.hpp.
| typedef slip::Point4d<char> slip::Point4d_c |
char alias
Definition at line 269 of file Point4d.hpp.
| typedef slip::Point4d<double> slip::Point4d_d |
double alias
Definition at line 253 of file Point4d.hpp.
| typedef slip::Point4d<float> slip::Point4d_f |
float alias
Definition at line 255 of file Point4d.hpp.
| typedef slip::Point4d<int> slip::Point4d_i |
int alias
Definition at line 265 of file Point4d.hpp.
| typedef slip::Point4d<long> slip::Point4d_l |
long alias
Definition at line 257 of file Point4d.hpp.
| typedef slip::Point4d<short> slip::Point4d_s |
short alias
Definition at line 261 of file Point4d.hpp.
| typedef slip::Point4d<unsigned char> slip::Point4d_uc |
unsigned char alias
Definition at line 271 of file Point4d.hpp.
| typedef slip::Point4d<unsigned int> slip::Point4d_ui |
unsigned int alias
Definition at line 267 of file Point4d.hpp.
| typedef slip::Point4d<unsigned long> slip::Point4d_ul |
unsigned long alias
Definition at line 259 of file Point4d.hpp.
| typedef slip::Point4d<unsigned short> slip::Point4d_us |
unsigned long alias
Definition at line 263 of file Point4d.hpp.
| typedef RegularVector2dField2d<double,double> slip::Regular2D3C_d |
double alias
Definition at line 1309 of file RegularVector2dField2d.hpp.
| typedef RegularVector2dField2d<float,double> slip::Regular2D3C_f |
float alias
Definition at line 1311 of file RegularVector2dField2d.hpp.
| typedef RegularVector2dField2d<double,double> slip::Regular2D3Cd |
double alias
Definition at line 1305 of file RegularVector2dField2d.hpp.
| typedef RegularVector2dField2d<float,double> slip::Regular2D3Cf |
float alias
Definition at line 1307 of file RegularVector2dField2d.hpp.
| typedef RegularVector3dField3d<double,double> slip::Regular3D3C_d |
double alias
Definition at line 1847 of file RegularVector3dField3d.hpp.
| typedef RegularVector3dField3d<float,double> slip::Regular3D3C_f |
float alias
Definition at line 1849 of file RegularVector3dField3d.hpp.
| typedef RegularVector3dField3d<double,double> slip::Regular3D3Cd |
double alias
Definition at line 1843 of file RegularVector3dField3d.hpp.
| typedef RegularVector3dField3d<float,double> slip::Regular3D3Cf |
float alias
Definition at line 1845 of file RegularVector3dField3d.hpp.
| typedef slip::RegularVector2dField2d<char,double> slip::RegularVector2dField2d_c |
char alias
Definition at line 1330 of file RegularVector2dField2d.hpp.
| typedef slip::RegularVector2dField2d<double,double> slip::RegularVector2dField2d_d |
double alias
Definition at line 1314 of file RegularVector2dField2d.hpp.
| typedef slip::RegularVector2dField2d<float,double> slip::RegularVector2dField2d_f |
float alias
Definition at line 1316 of file RegularVector2dField2d.hpp.
| typedef slip::RegularVector2dField2d<int,double> slip::RegularVector2dField2d_i |
int alias
Definition at line 1326 of file RegularVector2dField2d.hpp.
| typedef slip::RegularVector2dField2d<long,double> slip::RegularVector2dField2d_l |
long alias
Definition at line 1318 of file RegularVector2dField2d.hpp.
| typedef slip::RegularVector2dField2d<short,double> slip::RegularVector2dField2d_s |
short alias
Definition at line 1322 of file RegularVector2dField2d.hpp.
| typedef slip::RegularVector2dField2d<unsigned char,double> slip::RegularVector2dField2d_uc |
unsigned char alias
Definition at line 1332 of file RegularVector2dField2d.hpp.
| typedef slip::RegularVector2dField2d<unsigned int,double> slip::RegularVector2dField2d_ui |
unsigned int alias
Definition at line 1328 of file RegularVector2dField2d.hpp.
| typedef slip::RegularVector2dField2d<unsigned long,double> slip::RegularVector2dField2d_ul |
unsigned long alias
Definition at line 1320 of file RegularVector2dField2d.hpp.
| typedef slip::RegularVector2dField2d<unsigned short,double> slip::RegularVector2dField2d_us |
unsigned long alias
Definition at line 1324 of file RegularVector2dField2d.hpp.
| typedef slip::RegularVector3dField3d<char,double> slip::RegularVector3dField3d_c |
char alias
Definition at line 1868 of file RegularVector3dField3d.hpp.
| typedef slip::RegularVector3dField3d<double,double> slip::RegularVector3dField3d_d |
double alias
Definition at line 1852 of file RegularVector3dField3d.hpp.
| typedef slip::RegularVector3dField3d<float,float> slip::RegularVector3dField3d_f |
float alias
Definition at line 1854 of file RegularVector3dField3d.hpp.
| typedef slip::RegularVector3dField3d<int,double> slip::RegularVector3dField3d_i |
int alias
Definition at line 1864 of file RegularVector3dField3d.hpp.
| typedef slip::RegularVector3dField3d<long,double> slip::RegularVector3dField3d_l |
long alias
Definition at line 1856 of file RegularVector3dField3d.hpp.
| typedef slip::RegularVector3dField3d<short,double> slip::RegularVector3dField3d_s |
short alias
Definition at line 1860 of file RegularVector3dField3d.hpp.
| typedef slip::RegularVector3dField3d<unsigned char,double> slip::RegularVector3dField3d_uc |
unsigned char alias
Definition at line 1870 of file RegularVector3dField3d.hpp.
| typedef slip::RegularVector3dField3d<unsigned int,double> slip::RegularVector3dField3d_ui |
unsigned int alias
Definition at line 1866 of file RegularVector3dField3d.hpp.
| typedef slip::RegularVector3dField3d<unsigned long,double> slip::RegularVector3dField3d_ul |
unsigned long alias
Definition at line 1858 of file RegularVector3dField3d.hpp.
| typedef slip::RegularVector3dField3d<unsigned short,double> slip::RegularVector3dField3d_us |
unsigned long alias
Definition at line 1862 of file RegularVector3dField3d.hpp.
| typedef slip::Signal<char> slip::Signal_c |
char alias
Definition at line 1107 of file Signal.hpp.
| typedef slip::Signal<double> slip::Signal_d |
double alias
Definition at line 1091 of file Signal.hpp.
| typedef slip::Signal<float> slip::Signal_f |
float alias
Definition at line 1093 of file Signal.hpp.
| typedef slip::Signal<int> slip::Signal_i |
int alias
Definition at line 1103 of file Signal.hpp.
| typedef slip::Signal<long> slip::Signal_l |
long alias
Definition at line 1095 of file Signal.hpp.
| typedef slip::Signal<short> slip::Signal_s |
short alias
Definition at line 1099 of file Signal.hpp.
| typedef slip::Signal<unsigned char> slip::Signal_uc |
unsigned char alias
Definition at line 1109 of file Signal.hpp.
| typedef slip::Signal<unsigned int> slip::Signal_ui |
unsigned int alias
Definition at line 1105 of file Signal.hpp.
| typedef slip::Signal<unsigned long> slip::Signal_ul |
unsigned long alias
Definition at line 1097 of file Signal.hpp.
| typedef slip::Signal<unsigned short> slip::Signal_us |
unsigned long alias
Definition at line 1101 of file Signal.hpp.
| typedef slip::Vector2d<char> slip::Vector2d_c |
char alias
Definition at line 397 of file Vector2d.hpp.
| typedef slip::Vector2d<double> slip::Vector2d_d |
double alias
Definition at line 381 of file Vector2d.hpp.
| typedef slip::Vector2d<float> slip::Vector2d_f |
float alias
Definition at line 383 of file Vector2d.hpp.
| typedef slip::Vector2d<int> slip::Vector2d_i |
int alias
Definition at line 393 of file Vector2d.hpp.
| typedef slip::Vector2d<long> slip::Vector2d_l |
long alias
Definition at line 385 of file Vector2d.hpp.
| typedef slip::Vector2d<short> slip::Vector2d_s |
short alias
Definition at line 389 of file Vector2d.hpp.
| typedef slip::Vector2d<unsigned char> slip::Vector2d_uc |
unsigned char alias
Definition at line 399 of file Vector2d.hpp.
| typedef slip::Vector2d<unsigned int> slip::Vector2d_ui |
unsigned int alias
Definition at line 395 of file Vector2d.hpp.
| typedef slip::Vector2d<unsigned long> slip::Vector2d_ul |
unsigned long alias
Definition at line 387 of file Vector2d.hpp.
| typedef slip::Vector2d<unsigned short> slip::Vector2d_us |
unsigned long alias
Definition at line 391 of file Vector2d.hpp.
| typedef slip::Vector3d<char> slip::Vector3d_c |
char alias
Definition at line 414 of file Vector3d.hpp.
| typedef slip::Vector3d<double> slip::Vector3d_d |
double alias
Definition at line 398 of file Vector3d.hpp.
| typedef slip::Vector3d<float> slip::Vector3d_f |
float alias
Definition at line 400 of file Vector3d.hpp.
| typedef slip::Vector3d<int> slip::Vector3d_i |
int alias
Definition at line 410 of file Vector3d.hpp.
| typedef slip::Vector3d<long> slip::Vector3d_l |
long alias
Definition at line 402 of file Vector3d.hpp.
| typedef slip::Vector3d<short> slip::Vector3d_s |
short alias
Definition at line 406 of file Vector3d.hpp.
| typedef slip::Vector3d<unsigned char> slip::Vector3d_uc |
unsigned char alias
Definition at line 416 of file Vector3d.hpp.
| typedef slip::Vector3d<unsigned int> slip::Vector3d_ui |
unsigned int alias
Definition at line 412 of file Vector3d.hpp.
| typedef slip::Vector3d<unsigned long> slip::Vector3d_ul |
unsigned long alias
Definition at line 404 of file Vector3d.hpp.
| typedef slip::Vector3d<unsigned short> slip::Vector3d_us |
unsigned long alias
Definition at line 408 of file Vector3d.hpp.
| typedef slip::Vector4d<char> slip::Vector4d_c |
char alias
Definition at line 432 of file Vector4d.hpp.
| typedef slip::Vector4d<double> slip::Vector4d_d |
double alias
Definition at line 416 of file Vector4d.hpp.
| typedef slip::Vector4d<float> slip::Vector4d_f |
float alias
Definition at line 418 of file Vector4d.hpp.
| typedef slip::Vector4d<int> slip::Vector4d_i |
int alias
Definition at line 428 of file Vector4d.hpp.
| typedef slip::Vector4d<long> slip::Vector4d_l |
long alias
Definition at line 420 of file Vector4d.hpp.
| typedef slip::Vector4d<short> slip::Vector4d_s |
short alias
Definition at line 424 of file Vector4d.hpp.
| typedef slip::Vector4d<unsigned char> slip::Vector4d_uc |
unsigned char alias
Definition at line 434 of file Vector4d.hpp.
| typedef slip::Vector4d<unsigned int> slip::Vector4d_ui |
unsigned int alias
Definition at line 430 of file Vector4d.hpp.
| typedef slip::Vector4d<unsigned long> slip::Vector4d_ul |
unsigned long alias
Definition at line 422 of file Vector4d.hpp.
| typedef slip::Vector4d<unsigned short> slip::Vector4d_us |
unsigned long alias
Definition at line 426 of file Vector4d.hpp.
| typedef slip::Vector<char> slip::Vector_c |
char alias
Definition at line 1093 of file Vector.hpp.
| typedef slip::Vector<double> slip::Vector_d |
double alias
Definition at line 1077 of file Vector.hpp.
| typedef slip::Vector<float> slip::Vector_f |
float alias
Definition at line 1079 of file Vector.hpp.
| typedef slip::Vector<int> slip::Vector_i |
int alias
Definition at line 1089 of file Vector.hpp.
| typedef slip::Vector<long> slip::Vector_l |
long alias
Definition at line 1081 of file Vector.hpp.
| typedef slip::Vector<short> slip::Vector_s |
short alias
Definition at line 1085 of file Vector.hpp.
| typedef slip::Vector<unsigned char> slip::Vector_uc |
unsigned char alias
Definition at line 1095 of file Vector.hpp.
| typedef slip::Vector<unsigned int> slip::Vector_ui |
unsigned int alias
Definition at line 1091 of file Vector.hpp.
| typedef slip::Vector<unsigned long> slip::Vector_ul |
unsigned long alias
Definition at line 1083 of file Vector.hpp.
| typedef slip::Vector<unsigned short> slip::Vector_us |
unsigned long alias
Definition at line 1087 of file Vector.hpp.
| typedef slip::Volume<char> slip::Volume_c |
char alias
Definition at line 3644 of file Volume.hpp.
| typedef slip::Volume<double> slip::Volume_d |
double alias
Definition at line 3628 of file Volume.hpp.
| typedef slip::Volume<float> slip::Volume_f |
float alias
Definition at line 3630 of file Volume.hpp.
| typedef slip::Volume<int> slip::Volume_i |
int alias
Definition at line 3640 of file Volume.hpp.
| typedef slip::Volume<long> slip::Volume_l |
long alias
Definition at line 3632 of file Volume.hpp.
| typedef slip::Volume<short> slip::Volume_s |
short alias
Definition at line 3636 of file Volume.hpp.
| typedef slip::Volume<unsigned char> slip::Volume_uc |
unsigned char alias
Definition at line 3646 of file Volume.hpp.
| typedef slip::Volume<unsigned int> slip::Volume_ui |
unsigned int alias
Definition at line 3642 of file Volume.hpp.
| typedef slip::Volume<unsigned long> slip::Volume_ul |
unsigned long alias
Definition at line 3634 of file Volume.hpp.
| typedef slip::Volume<unsigned short> slip::Volume_us |
unsigned long alias
Definition at line 3638 of file Volume.hpp.
Choose between different border treatment modes for convolution algorithms.
| Enumerator | |
|---|---|
| BORDER_TREATMENT_AVOID | |
| BORDER_TREATMENT_ZERO_PADDED | |
| BORDER_TREATMENT_NEUMANN | |
| BORDER_TREATMENT_CIRCULAR | |
| BORDER_TREATMENT_REFLECT | |
| BORDER_TREATMENT_COPY | |
Definition at line 117 of file border_treatment.hpp.
Choose between different types of crosscorrelation.
| Enumerator | |
|---|---|
| CC | |
| CCC | |
| PNCC | |
| NCC | |
Definition at line 121 of file correlation.hpp.
| enum slip::DECOMP_TYPE |
| Enumerator | |
|---|---|
| RQ | |
| direct | |
Definition at line 92 of file camera_algo.hpp.
Indicate the type of a dense matrix.
Definition at line 134 of file linear_algebra.hpp.
Choose between different directions in a 4D space.
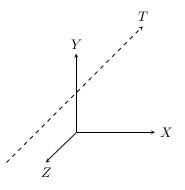
| Enumerator | |
|---|---|
| T_DIRECTION | |
| S_DIRECTION | |
| R_DIRECTION | |
| C_DIRECTION | |
Definition at line 824 of file derivatives.hpp.
| enum slip::NEIGHBOURHOOD |
Choose between different neighbourhood.
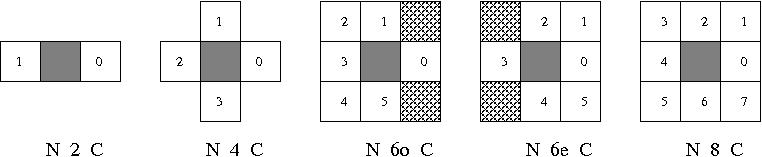
| Enumerator | |
|---|---|
| N_2_C | |
| N_4_C | |
| N_6o_C | |
| N_6e_C | |
| N_8_C | |
| N_6_C | |
| N_18_C | |
| N_26_C | |
| N_4D_8_C | |
Definition at line 119 of file neighbors.hpp.
Choose between different border treatment modes for convolution algorithms.
| Enumerator | |
|---|---|
| AFFINE_FUNCTION | |
| NORMAL_FUNCTION | |
| SIGMOID_FUNCTION | |
Definition at line 107 of file dynamic.hpp.
Choose between different plane orientations.
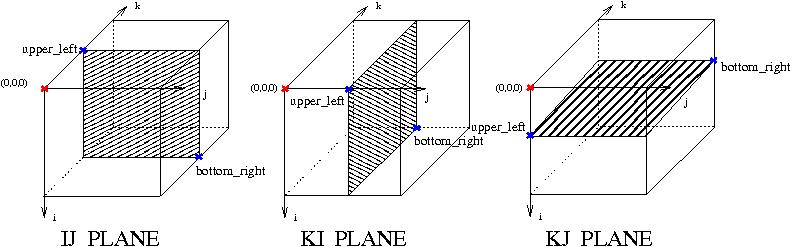
| Enumerator | |
|---|---|
| IJ_PLANE | |
| KJ_PLANE | |
| KI_PLANE | |
Definition at line 109 of file iterator3d_plane.hpp.
Choose between different spatial directions.
| Enumerator | |
|---|---|
| X_DIRECTION | |
| Y_DIRECTION | |
| Z_DIRECTION | |
Definition at line 120 of file derivatives.hpp.
|
related |
Definition at line 1435 of file KVector.hpp.
|
related |
Definition at line 2013 of file Vector.hpp.
|
related |
Definition at line 2026 of file Signal.hpp.
|
related |
Definition at line 3892 of file Matrix.hpp.
|
related |
Definition at line 5064 of file HyperVolume.hpp.
|
related |
Definition at line 5073 of file Matrix4d.hpp.
|
related |
Definition at line 5714 of file Matrix3d.hpp.
|
related |
Definition at line 6031 of file Volume.hpp.
|
related |
Definition at line 1464 of file KVector.hpp.
|
related |
Definition at line 1473 of file KVector.hpp.
|
related |
Definition at line 1482 of file KVector.hpp.
|
related |
Definition at line 2041 of file Vector.hpp.
|
related |
Definition at line 2049 of file Vector.hpp.
|
related |
Definition at line 2054 of file Signal.hpp.
|
related |
Definition at line 2057 of file Vector.hpp.
|
related |
Definition at line 2062 of file Signal.hpp.
|
related |
Definition at line 2070 of file Signal.hpp.
|
related |
Definition at line 3920 of file Matrix.hpp.
|
related |
Definition at line 3928 of file Matrix.hpp.
|
related |
Definition at line 3936 of file Matrix.hpp.
|
related |
Definition at line 5092 of file HyperVolume.hpp.
|
related |
Definition at line 5101 of file Matrix4d.hpp.
|
related |
Definition at line 5742 of file Matrix3d.hpp.
|
related |
Definition at line 6059 of file Volume.hpp.
| void slip::add_border | ( | _II | first, |
| _II | last, | ||
| _OI | out_first, | ||
| _OI | out_last, | ||
| const slip::BORDER_TREATMENT | border, | ||
| const std::size_t | b_size = 1 |
||
| ) |
Adds the border of the range [first,last) according to the border condtion border and the border size b_size.
| first | RandomAccessIterator or RandomAccessIterator2d or RandomAccessIterator3d. |
| last | RandomAccessIterator or RandomAccessIterator2d or RandomAccessIterator3d. |
| out_first | RandomAccessIterator or RandomAccessIterator2d or RandomAccessIterator3d. |
| border | slip::BORDER_TREATMENT border condition. |
| b_size | Size of the border (1 by default). |
Definition at line 1191 of file border_treatment.hpp.
| void slip::add_border1d | ( | const Container1 & | in, |
| const slip::BORDER_TREATMENT | border_type, | ||
| Container2 & | out, | ||
| const std::size_t | border_size = 1 |
||
| ) |
Adds the border at a 1d container according to the border condition border and the border size b_size.
| in | input container. |
| border_type | slip::BORDER_TREATMENT border condition. |
| out | output container. |
| b_size | Size of the border (1 by default). |
Definition at line 1230 of file border_treatment.hpp.
| void slip::add_border2d | ( | const Container2d1 & | in, |
| const slip::BORDER_TREATMENT | border_type, | ||
| Container2d2 & | out, | ||
| const std::size_t | border_size = 1 |
||
| ) |
Adds the border at a 2d container according to the border condition border and the border size b_size.
| in | input container. |
| border_type | slip::BORDER_TREATMENT border condition. |
| out | output container. |
| b_size | Size of the border (1 by default). |
Definition at line 1270 of file border_treatment.hpp.
| void slip::add_border3d | ( | const Container3d1 & | in, |
| const slip::BORDER_TREATMENT | border_type, | ||
| Container3d2 & | out, | ||
| const std::size_t | border_size = 1 |
||
| ) |
Adds the border at a 3d container according to the border condition border and the border size b_size.
| in | input container. |
| border_type | slip::BORDER_TREATMENT border condition. |
| out | output container. |
| b_size | Size of the border (1 by default). |
Definition at line 1313 of file border_treatment.hpp.
| void slip::add_border4d | ( | const Container4d1 & | in, |
| const slip::BORDER_TREATMENT | border_type, | ||
| Container4d2 & | out, | ||
| const std::size_t | border_size = 1 |
||
| ) |
Adds the border at a 4d container according to the border condition border and the border size b_size.
| in | input container. |
| border_type | slip::BORDER_TREATMENT border condition. |
| out | output container. |
| b_size | Size of the border (1 by default). |
Definition at line 1360 of file border_treatment.hpp.
|
inline |
Add a gaussian noise to a container.
| first | begin InputIterator on datas |
| last | past-to-end InputIterator on datas |
| result | begin OutputIterator on results |
| mean | Mean of the gaussian noise. |
| var | Standard deviation of the gaussian noise. |
|
inline |
Add a gaussian noise to a container according to a predicate.
| first | begin InputIterator on datas |
| last | past-to-end InputIterator on datas |
| result | begin OutputIterator on results |
| pred | a predicate |
| mean | Mean of the gaussian noise. |
| var | Standard deviation of the gaussian noise. |
|
inline |
Add a gaussian noise to a container according to a mask sequence.
| first | begin InputIterator on datas |
| last | past-to-end InputIterator on datas |
| mask_first | An inputIterator. |
| result | begin OutputIterator on results |
| mean | Mean of the gaussian noise. |
| var | Standard deviation of the gaussian noise. |
| value | true value of the mask range. Default is 1. |
|
inline |
Add a salt and pepper noise to a container.
| first | begin InputIterator on datas |
| last | past-to-end Inputiterator on datas |
| result | begin OutputIterator on results |
| density | Density of noisy items |
| salt_value | Value used for "white" items |
| pepper_value | Value used for "black" items |
|
inline |
Add a salt and pepper noise to a container according to a predicate.
| first | begin InputIterator on datas |
| last | past-to-end InputIterator on datas |
| result | begin OutputIterator on results |
| pred | A predicate. |
| density | Density of noisy items |
| salt_value | Value used for "white" items |
| pepper_value | Value used for "black" items |
|
inline |
Add a salt and pepper noise to a container according to a mask sequence.
| first | begin InputIterator on datas |
| last | past-to-end InputIterator on datas |
| mask_first | An inputIterator. |
| result | begin OutputIterator on results |
| density | Density of noisy items |
| salt_value | Value used for "white" items |
| pepper_value | Value used for "black" items |
| value | true value of the mask range. Default is 1. |
|
inline |
Add a speckle noise to a container.
| first | begin InputIterator on datas |
| last | past-to-end InputIterator on datas |
| result | begin OutputIterator on results |
| var | Standard deviation of the speckle noise. |
|
inline |
Add a speckle noise to a container according to a predicate.
| first | begin InputIterator on datas |
| last | past-to-end InputIterator on datas |
| result | begin OutputIterator on results |
| pred | a predicate |
| var | Standard deviation of the speckle noise. |
|
inline |
Add a speckle noise to a container according to a mask sequence.
| first | begin InputIterator on datas |
| last | past-to-end InputIterator on datas |
| mask_first | An inputIterator. |
| result | begin OutputIterator on results |
| var | Standard deviation of the speckle noise. |
| value | true value of the mask range. Default is 1. |
|
inline |
Add a uniform noise to a container.
| first | begin InputIterator on datas |
| last | past-to-end InputIterator on datas |
| result | begin. OutputIterator on results |
| min | Minimum noise value |
| max | Maximum noise value |
|
inline |
Add a uniform noise to a container according to a predicate.
| first | begin InputIterator on datas |
| last | past-to-end InputIterator on datas |
| result | begin OutputIterator on results |
| pred | an predicate. |
| min | Minimum noise value |
| max | Maximum noise value |
|
inline |
Add a uniform noise to a container according to mask sequence.
| first | begin InputIterator on datas |
| last | past-to-end InputIterator on datas |
| mask_first | An inputIterator. |
| result | begin OutputIterator on results |
| min | Minimum noise value |
| max | Maximum noise value |
| value | true value of the mask range. Default is 1. |
|
inline |
Analyse the type of a matrix.
| A_up | 2D iterator on the upper_left element of A container. |
| A_bot | 2D iterator on the bottom_right element of A container. |
| tol | Tolerance (epsilon by default). |
Definition at line 4785 of file linear_algebra.hpp.
|
inline |
Applies a C-function to each element of a range.
| first | An InputIterator. |
| last | An InputIterator. |
| result | An OutputIterator. |
| function | A one parameter C-function. |
Applies the C-function function to each element in the input range and assigns the results to successive elements of the output range. Applies the following code
|
inline |
Applies a C-function to each element of a range.
| first | An InputIterator. |
| last | An InputIterator. |
| result | An OutputIterator. |
| function | A one const-parameter C-function. |
Applies the C-function function to each element in the input range and assigns the results to successive elements of the output range. Applies the following code
|
inline |
Applies a two-parameter C-function to each element of two ranges.
| first | An InputIterator. |
| last | An InputIterator. |
| first2 | An InputIterator. |
| result | An OutputIterator. |
| function | A two-parameter C-function. |
Applies the C-function function to each element in the two input ranges and assigns the results to successive elements of the output range. Applies the following code
|
inline |
Applies a two-const-parameter C-function to each element of two ranges.
| first | An InputIterator. |
| last | An InputIterator. |
| first2 | An InputIterator. |
| result | An OutputIterator. |
| function | A two-parameter C-function. |
Applies the C-function function to each element in the two input ranges and assigns the results to successive elements of the output range. Applies the following code
|
inline |
Applies a C-function to each element of a range according to a predicate.
| first | An InputIterator. |
| last | An InputIterator. |
| result | An OutputIterator. |
| pred | A predicate. |
| function | A one parameter C-function. |
|
inline |
Applies a C-function to each element of a range according to a predicate.
| first | An InputIterator. |
| last | An InputIterator. |
| result | An OutputIterator. |
| pred | A predicate. |
| function | A one parameter C-function. |
|
inline |
Applies a C-function to each element of a range according to a predicate.
| first | An InputIterator. |
| last | An InputIterator. |
| first2 | An InputIterator. |
| result | An OutputIterator. |
| pred | A predicate. |
| function | A two-parameter C-function |
|
inline |
Applies a C-function to each element of a range according to a predicate.
| first | An InputIterator. |
| last | An InputIterator. |
| first2 | An InputIterator. |
| result | An OutputIterator. |
| pred | A predicate. |
| function | A two-parameter C-function |
|
inline |
Applies a C-function to each element of a range according to a mask range.
| first | An InputIterator. |
| last | An InputIterator. |
| mask_first | An InputIterator. |
| result | An OutputIterator. |
| function | A one parameter C-function. |
| value | true value of the mask range. Default is 1. |
|
inline |
Applies a C-function to each element of a range according to a mask range.
| first | An InputIterator. |
| last | An InputIterator. |
| mask_first | An InputIterator. |
| result | An OutputIterator. |
| function | A one parameter C-function. |
| value | true value of the mask range. Default is 1. |
|
inline |
Applies a C-function to each element of a range according to a mask range.
| first | An InputIterator. |
| last | An InputIterator. |
| mask_first | An InputIterator. |
| first2 | An InputIterator. |
| result | An OutputIterator. |
| function | A two-parameter C-function |
| value | true value of the mask range. Default is 1. |
|
inline |
Applies a C-function to each element of a range according to a mask range.
| first | An InputIterator. |
| last | An InputIterator. |
| mask_first | An InputIterator. |
| first2 | An InputIterator. |
| result | An OutputIterator. |
| function | A two-parameter C-function |
| value | true value of the mask range. Default is 1. |
|
related |
Definition at line 1501 of file KVector.hpp.
|
related |
Definition at line 1510 of file KVector.hpp.
|
related |
Definition at line 1519 of file KVector.hpp.
|
related |
Definition at line 2076 of file Vector.hpp.
|
related |
Definition at line 2084 of file Vector.hpp.
|
related |
Definition at line 2089 of file Signal.hpp.
|
related |
Definition at line 2092 of file Vector.hpp.
|
related |
Definition at line 2097 of file Signal.hpp.
|
related |
Definition at line 2105 of file Signal.hpp.
|
related |
Definition at line 3954 of file Matrix.hpp.
|
related |
Definition at line 3962 of file Matrix.hpp.
|
related |
Definition at line 3970 of file Matrix.hpp.
|
related |
Definition at line 5110 of file HyperVolume.hpp.
|
related |
Definition at line 5119 of file Matrix4d.hpp.
|
related |
Definition at line 5760 of file Matrix3d.hpp.
|
related |
Definition at line 6077 of file Volume.hpp.
|
related |
Definition at line 1539 of file KVector.hpp.
|
related |
Definition at line 1548 of file KVector.hpp.
|
related |
Definition at line 1557 of file KVector.hpp.
|
related |
Definition at line 2109 of file Vector.hpp.
|
related |
Definition at line 2117 of file Vector.hpp.
|
related |
Definition at line 2122 of file Signal.hpp.
|
related |
Definition at line 2125 of file Vector.hpp.
|
related |
Definition at line 2130 of file Signal.hpp.
|
related |
Definition at line 2138 of file Signal.hpp.
|
related |
Definition at line 3988 of file Matrix.hpp.
|
related |
Definition at line 3996 of file Matrix.hpp.
|
related |
Definition at line 4004 of file Matrix.hpp.
|
related |
Definition at line 5128 of file HyperVolume.hpp.
|
related |
Definition at line 5137 of file Matrix4d.hpp.
|
related |
Definition at line 5778 of file Matrix3d.hpp.
|
related |
Definition at line 6095 of file Volume.hpp.
|
inline |
Computes the autocorrelations from lag -(last-first) to (last-first) of a range [first,last).
| first | A RandomAccessIterator to the data. |
| last | A RandomAccessIterator to the data. |
| auto_first | A RandomAccessIterator to the autocorrelations range. |
| auto_last | A RandomAccessIterator to the autocorrelations range. |
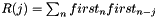
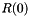 corresponds the energy of the data
corresponds the energy of the dataDefinition at line 1581 of file correlation.hpp.
|
inline |
Computes the autocorrelations from lag -(last-first) to (last-first) of a range [first,last).
| first | A RandomAccessIterator to the data. |
| last | A RandomAccessIterator to the data. |
| auto_first | A RandomAccessIterator to the autocorrelations range. |
| auto_last | A RandomAccessIterator to the autocorrelations range. |
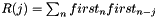
 corresponds the energy of the data
corresponds the energy of the dataDefinition at line 1518 of file correlation.hpp.
|
inline |
Computes the autocovariance from lag -(last-first) to 0 of a range [first,last).
| first | A RandomAccessIterator to the data. |
| last | A RandomAccessIterator to the data. |
| auto_first | A RandomAccessIterator to the autocorrelations range. |
| auto_last | A RandomAccessIterator to the autocorrelations range. |
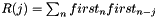
 corresponds the energy of the data
corresponds the energy of the dataDefinition at line 1750 of file correlation.hpp.
|
inline |
Computes the saxpy ("scalar a x plus b") for each element of two ranges x and y.
| a | A scalar value |
| first1 | iterator to the beginning of the first sequence (X) |
| last1 | iterator to the end of the first sequence (X) |
| first2 | iterator to the beginning of the second sequence (Y) |
Definition at line 632 of file linear_algebra.hpp.
|
inline |
applies a diagonal similarity transform to the square matrix A to make the rows and columns as close in norm as possible. Balancing may reduce the 1-norm of the matrix, and improves the accuracy of the computed eigenvalues and/or eigenvectors. To avoid round-off errors, balance scales A with powers of 2. A is replaced by the balanced matrix which has the same eigenvalues and singular values : 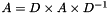
| A | |
| D | diagonal scaling matrix |
Definition at line 110 of file linear_algebra_qr.hpp.
|
inline |
in place Band LU decomposition a square band Matrix A 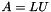 with L a p lower band matrix and U a q upper band matrix
with L a p lower band matrix and U a q upper band matrix
| A_up | 2D iterator corresponding to the upper_left element of the matrix A |
| A_bot | 2D iterator corresponding to one past-the-end bottom_right of the matrix A |
| p | Width of the lower band of A. |
| q | Width of the upper_band of A |
| Ind_first | RandomAccessIterator to the first element of the permutation vector. |
| Ind_last | RandomAccessIterator to one past-the-end element of the permutation vector. |
| precision |
Definition at line 6773 of file linear_algebra.hpp.
|
inline |
in place Band LU decomposition a square band Matrix A 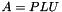 with L a p lower band matrix and U a q upper band matrix and P the permutation matrix.
with L a p lower band matrix and U a q upper band matrix and P the permutation matrix.
| M | The matrix M. |
| p | Width of the lower band of A. |
| q | Width of the upper_band of A. |
| L | The matrix L. |
| U | The matrix U. |
| P | The matrix P. |
| precision |
Definition at line 6902 of file linear_algebra.hpp.
| void slip::BdBacksearch | ( | Vector & | d, |
| Vector & | e, | ||
| const typename slip::lin_alg_traits< typename Vector::value_type >::value_type | tol, | ||
| SizeType & | l, | ||
| SizeType & | i1, | ||
| SizeType & | i2 | ||
| ) |
Back searching a bidiagonal Matrix this algorithm takes a bidiagobal matrix B, a tolerance tol and an index l(0<=l<=p-1) and determines indices i1,i2<=l such one of the following condictions holds 1) 0<=i1<i2<=l, in which case the matrix deflates as rows i1 and i2. 2) 0=i1=i2, in which case all the superdiagonal elements of B in rows 0 through l-1 are zero.
| d | The diagonal vector of B. |
| e | The lower diagonal vector of B. |
| tol | the relative error we can expect from setting the curent superdiagonal to zero |
| l | maximum index |
| i1 | first index |
| i2 | second index |
Definition at line 459 of file linear_algebra_svd.hpp.
| void slip::Bi_complex_to_real | ( | Vector & | d, |
| Vector & | e, | ||
| Matrix & | U, | ||
| Matrix & | V | ||
| ) |
BiQR Given an upper bidiagonal matrix B, Bi_complex_to_real transforms the complex bidiagonal form into a real form. The tranformations from the left are accumulmated in the matrix U and the transformations from the right in the matrix V.
| U | 2D Container of the tranformations from the left n*p |
| V | 2D Container of the transformations from the right p*p |
| d | 1D Container size p |
| e | 1D Container.size p-1 |
Definition at line 277 of file linear_algebra_svd.hpp.
|
inline |
Computes the biased autocorrelations from lag -(last-first) to (last-first) of a range [first,last).
| first | A RandomAccessIterator to the data. |
| last | A RandomAccessIterator to the data. |
| auto_first | A RandomAccessIterator to the autocorrelations range. |
| auto_last | A RandomAccessIterator to the autocorrelations range. |
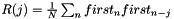
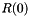 corresponds the energy of the data
corresponds the energy of the dataDefinition at line 1642 of file correlation.hpp.
|
inline |
Constructs the biased autocorrelation matrix from given a range.
| first | RandomAccessIterator to the first element of the data. |
| last | RandomAccessIterator to one past-the-end element of the data. |
| A | The resulting biased autocorrelation matrix. |
Definition at line 1914 of file correlation.hpp.
|
inline |
Computes the biased autocovariance from lag -(last-first) to 0 of a range [first,last).
| first | A RandomAccessIterator to the data. |
| last | A RandomAccessIterator to the data. |
| auto_first | A RandomAccessIterator to the autocorrelations range. |
| auto_last | A RandomAccessIterator to the autocorrelations range. |
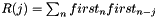
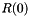 corresponds the energy of the data
corresponds the energy of the dataDefinition at line 1813 of file correlation.hpp.
|
inline |
Constructs the biased autocorrelation matrix from given a range.
| first | RandomAccessIterator to the first element of the data. |
| last | RandomAccessIterator to one past-the-end element of the data. |
| A | The resulting biased autocovariance matrix. |
Definition at line 1953 of file correlation.hpp.
|
inline |
binarize algorithm
| first | begin InputIterator of the range to binarize |
| last | past-the-end InputIterator of the range to binarize |
| result | begin OutputIterator of the resulting range |
| t_value | binarize value |
| false_value | result value when *first <= t_value |
| true_value | result value when *first > t_value |
Definition at line 194 of file threshold.hpp.
| void slip::BiQR | ( | Vector & | d, |
| Vector & | e, | ||
| Real & | sigma, | ||
| const SizeType & | row1, | ||
| const SizeType & | row2, | ||
| Matrix & | U, | ||
| Matrix & | V | ||
| ) |
BiQR Given an upper bidiagonal matrix B and a shift sigma, BiQR performs a QR step between rows row1 ans row2. The tranformations from the left are accumulmated in the matrix U and the transformations from the right in the matrix V.
| d | 1D Container size p |
| e | 1D Container.size p-1 |
| sigma | shift value. |
| row1 | first row index. |
| row2 | second row index. |
| U | 2D Container of the tranformations from the left n*p |
| V | 2D Container of the transformations from the right p*p |
Definition at line 343 of file linear_algebra_svd.hpp.
| void slip::BiReduce | ( | Matrix1 & | X, |
| Vector & | d, | ||
| Vector & | e, | ||
| Matrix2 & | U, | ||
| Matrix3 & | V | ||
| ) |
BiReduce. Given an n*p matrix X with n>=p Bireduce reduce X to an upper bidiagola form The tranformations from the left are accumulmated in the n*p matrix U and the transformations from the right in the matrix V. on return X contains the genrators of the householder transformation used in the reduction X=U[d,e]V.
| X | 2D Container of the input Matrix n*p |
| U | 2D Container of the tranformations from the left n*p |
| V | 2D Container of the transformations from the right p*p |
| d | 1D Container |
| e | 1D Container. |
Definition at line 148 of file linear_algebra_svd.hpp.
|
inline |
|
inline |
Computes the cardinal or the number of elements of a range.
| first | An InputIterator. |
| last | An InputIterator. |
Definition at line 285 of file statistics.hpp.
|
inline |
Computes the cardinal or the number of elements of a range using a predicate.
| first | An InputIterator. |
| last | An InputIterator. |
| pred | a predicate function |
Definition at line 2605 of file statistics.hpp.
|
inline |
Computes the cardinal or the number of elements of a mask range.
| mask_first | An InputIterator of a mask Iterator. |
| mask_last | An InputIterator of a mask Iterator. |
| value | Mask value. |
Definition at line 2221 of file statistics.hpp.
|
inline |
Computes the standard crosscorrelation between two sequences: 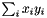 . Multiplies successive elements from the two ranges and adds each product into the accumulated value using operator+(). The values in the ranges are processed in order.
. Multiplies successive elements from the two ranges and adds each product into the accumulated value using operator+(). The values in the ranges are processed in order.
| first | An InputIterator. |
| last | An InputIterator. |
| first2 | An InputIterator. |
Definition at line 339 of file correlation.hpp.
| T slip::cc_if | ( | InputIterator1 | first1, |
| InputIterator1 | last1, | ||
| InputIterator2 | first2, | ||
| Predicate | pred | ||
| ) |
Computes the standard crosscorrelation between two sequences according to a Predicate. 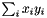 .
.
| first1 | An InputIterator. |
| last1 | An InputIterator. |
| first2 | An InputIterator. |
| pred | A predicate. |
Definition at line 429 of file correlation.hpp.
|
inline |
Computes the standard crosscorrelation between two sequences according to a mask sequence 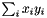 . Multiplies successive elements from the two ranges accordind to a mask sequence and adds each product according to the mask range into the accumulated value using operator+(). The values in the ranges are processed in order.
. Multiplies successive elements from the two ranges accordind to a mask sequence and adds each product according to the mask range into the accumulated value using operator+(). The values in the ranges are processed in order.
| first1 | An InputIterator. |
| last1 | An InputIterator. |
| mask_first | An InputIterator. |
| first2 | An InputIterator. |
| value | true value of the mask range. Default is 1. |
Definition at line 382 of file correlation.hpp.
|
inline |
Computes the centered crosscorrelation between two sequences: 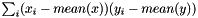 .
.
| first | An InputIterator. |
| last | An InputIterator. |
| first2 | An InputIterator. |
| mean1 | mean value of the first range [first,last). |
| mean2 | mean value of the second range [first2, first2 + (last-first)). |
Definition at line 669 of file correlation.hpp.
|
inline |
Computes the standard crosscorrelation between two sequences according to a Predicate: 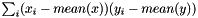 .
.
| first1 | An InputIterator. |
| last1 | An InputIterator. |
| first2 | An InputIterator. |
| pred | A predicate. |
| mean1 | mean value of the first range [first,last). |
| mean2 | mean value of the second range [first2, first2 + (last-first)). |
Definition at line 768 of file correlation.hpp.
|
inline |
Computes the centered crosscorrelation between two sequences according to a mask sequence 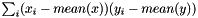 .
.
| first1 | An InputIterator. |
| last1 | An InputIterator. |
| mask_first | An InputIterator. |
| first2 | An InputIterator. |
| mean1 | mean value of the first range [first,last). |
| mean2 | mean value of the second range [first2, first2 + (last-first)). |
| value | true value of the mask range. Default is 1. |
Definition at line 715 of file correlation.hpp.
| void slip::center | ( | RandomAccessIterator | first, |
| RandomAccessIterator | last, | ||
| RandomAccessIterator2 | out_first | ||
| ) |
Substracts its mean to a range.
| first | RandomAccessIterator to the first element of the range. |
| last | RandomAccessIterator to one past-the-end element of the range. |
| out_first | RandomAccessIterator to the first element of the range. |
Definition at line 1381 of file statistics.hpp.
|
inline |
Substracts its mean to a range using a predicate.
| first | An InputIterator. |
| last | An InputIterator |
| pred | a predicate function |
| out_first | An OutputIterator |
Definition at line 3548 of file statistics.hpp.
|
inline |
Substracts its mean to a range according a mask.
| first | An InputIterator. |
| last | An InputIterator |
| mask_first | An InputIterator on the mask |
| out_first | An OuputIterator. |
| value | Mask value. |
Definition at line 2490 of file statistics.hpp.
|
inline |
Computes the centered crosscorrelation between two sequences: 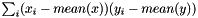 .
.
| first | An InputIterator. |
| last | An InputIterator. |
| first2 | An InputIterator. |
| mean1 | mean value of the first range [first,last). |
| mean2 | mean value of the second range [first2, first2 + (last-first)). |
Definition at line 488 of file correlation.hpp.
|
inline |
Computes the centered crosscorrelation between two Images.
| in1_upper_left | : A 2d input iterator (image). |
| in1_bottom_right | : A 2d input iterator (image). |
| in2_upper_left | : A 2d input iterator (mask). |
| in2_bottom_right | : A 2d input iterator (mask). |
| out_upper_left | : A 2d output iterator (result). |
| out_bottom_right | : A 2d output iterator (result). |
Definition at line 2147 of file correlation.hpp.
|
inline |
Computes the standard crosscorrelation between two sequences according to a Predicate: 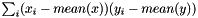 .
.
| first1 | An InputIterator. |
| last1 | An InputIterator. |
| first2 | An InputIterator. |
| pred | A predicate. |
| mean1 | mean value of the first range [first,last) (0 by default). |
| mean2 | mean value of the second range [first2, first2 + (last-first)) (0 by default). |
Definition at line 601 of file correlation.hpp.
|
inline |
Computes the centered crosscorrelation between two sequences according to a mask sequence 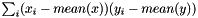 .
.
| first1 | An InputIterator. |
| last1 | An InputIterator. |
| mask_first | An InputIterator. |
| first2 | An InputIterator. |
| mean1 | mean value of the first range [first,last). |
| mean2 | mean value of the second range [first2, first2 + (last-first)). |
| value | true value of the mask range. Default is 1. |
Definition at line 542 of file correlation.hpp.
|
inline |
Changes the dynamic of a container.
| first | begin iterator of the input container |
| last | past-the-end iterator of the input container |
| result | begin iterator of the result container |
| dynamic_fun | Unary function |
Definition at line 357 of file dynamic.hpp.
|
inline |
Changes the dynamic of a container.
| first | InputIterator on the container. |
| last | InputIterator on the container. |
| result | OutputIterator on the result container. |
| fun | NORMALIZATION_FUNCTION : AFFINE_FUNCTION,SIGMOID_FUNCTION |
Definition at line 495 of file dynamic.hpp.
|
inline |
Changes the dynamic of a container according to a predicate.
| first | An InputIterator. |
| last | An InputIterator. |
| result | An output iterator. |
| pred | predicate. |
| dynamic_fun | Unary function |
Definition at line 464 of file dynamic.hpp.
|
inline |
Changes the dynamic of a container according to a mask sequence.
| first | An InputIterator. |
| last | An InputIterator. |
| result | An output iterator. |
| mask_first | An input iterator. |
| dynamic_fun | Unary function |
| value | true value of the mask range. Default is 1. |
Definition at line 406 of file dynamic.hpp.
|
inline |
Implements the three term recurrence relation for the Chebyshev multivariate polynomials, this function can be used to create a sequence of orthogonal polynomial, and for rising k. This recurrence relation holds for Chebychev Polynomials of both the first and second kinds:
![\[ 2xPk(x)-P_{k-1}\]](../../form_238.png)
.
| k | The degree of the last polynomial calculated. |
| x | The x polynomial. |
| Pk | The value of the polynomial evaluated at degree k. |
| Pkm1 | The value of the polynomial evaluated at degree k-1. |
Definition at line 295 of file polynomial_algo.hpp.
|
inline |
Implements the three term recurrence relation for the Chebyshev polynomials, this function can be used to create a sequence of orthogonal polynomial, and for rising k. This recurrence relation holds for Chebyshev Polynomials of both the first and second kinds:
![\[ P_{k+1}(x) = 2xP_k(x)-P_{k-1}(x)\]](../../form_237.png)
.
| k | The degree of the last polynomial calculated. |
| x | The x polynomial. |
| Pk | The value of the polynomial evaluated at degree k. |
| Pkm1 | The value of the polynomial evaluated at degree k-1. |
Definition at line 244 of file polynomial_algo.hpp.
|
inline |
Computes the Chi2 "distance" of two ranges : 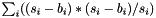 .
.
| first1 | An InputIterator. |
| last1 | An InputIterator. |
| first2 | An InputIterator. |
Definition at line 1921 of file compare.hpp.
|
inline |
Computes the Chi2 "distance" of two ranges according to a Predicate.
| first1 | An input iterator. |
| last1 | An input iterator. |
| first2 | An input iterator. |
| pred | A predicate. |
Definition at line 2020 of file compare.hpp.
|
inline |
Computes the Chi2 "distance" of two ranges according to a mask sequence : 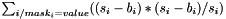 .
.
| first1 | An InputIterator. |
| last1 | An InputIterator. |
| mask_first | An input iterator. |
| first2 | An InputIterator. |
| value | true value of the mask range. Default is 1. |
Definition at line 1964 of file compare.hpp.
|
inline |
cholesky decomposition of a square hermitian positive definite Matrix. 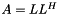 with L a lower triangular matrix
with L a lower triangular matrix
| A | 2D container. |
| L | 2D container. |
| LT | 2D container. |
Definition at line 10290 of file linear_algebra.hpp.
|
inline |
cholesky decomposition of a square hermitian positive definite Matrix. 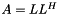 with L a lower triangular matrix. L is stored in the lower triangular part of A,
with L a lower triangular matrix. L is stored in the lower triangular part of A, 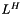 is stored in the upper triangular part of A.
is stored in the upper triangular part of A.
| A | 2D container. |
Definition at line 10348 of file linear_algebra.hpp.
|
inline |
cholesky decomposition of a square hermitian positive definite Matrix. 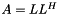 with L a lower triangular matrix
with L a lower triangular matrix
| A_up | 2D iterator corresponding to the upper_left element of the matrix A |
| A_bot | 2D iterator corresponding to one past-the-end bottom_right of the matrix A |
| L_up | 2D iterator corresponding to the upper_left element of the matrix L |
| L_bot | 2D iterator corresponding to one past-the-end bottom_right of the matrix L |
| LH_up | 2D iterator corresponding to the upper_left element of the matrix LH |
| LH_bot | 2D iterator corresponding to one past-the-end bottom_right of the matrix LH |
Definition at line 9822 of file linear_algebra.hpp.
|
inline |
cholesky decomposition of a square hermitian positive definite Matrix. 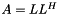 with L a lower triangular matrix. L is stored in the lower triangular part of A,
with L a lower triangular matrix. L is stored in the lower triangular part of A, 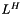 is stored in the upper triangular part of A.
is stored in the upper triangular part of A.
| A_up | 2D iterator corresponding to the upper_left element of the matrix A |
| A_bot | 2D iterator corresponding to one past-the-end bottom_right of the matrix A |
Definition at line 9913 of file linear_algebra.hpp.
|
inline |
cholesky decomposition of a square hermitian positive definite Matrix. 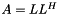 with L a lower triangular matrix
with L a lower triangular matrix
| A | 2D container. |
| L | 2D container. |
| LT | 2D container. |
Definition at line 10235 of file linear_algebra.hpp.
|
inline |
cholesky inverse of a square hermitian positive definite Matrix A.
| A_up | 2D iterator corresponding to the upper_left element of the matrix A |
| A_bot | 2D iterator corresponding to one past-the-end bottom_right of the matrix A |
| Ainv_up | 2D iterator corresponding to the upper_left element of the inverse matrix. |
| Ainv_bot | 2D iterator corresponding to one past-the-end bottom_right of the inverse matrix. |
| precision | 1.0E-6 by default. |
Definition at line 10550 of file linear_algebra.hpp.
|
inline |
cholesky inverse of a square hermitian positive definite Matrix A.
| A | The matrix to invert. |
| Ainv | The inverted matrix. |
| precision | 1.0E-6 by default. |
Definition at line 10637 of file linear_algebra.hpp.
|
inline |
cholesky decomposition of a square real symmetric and positive definite Matrix. 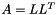 with L a lower triangular matrix.
with L a lower triangular matrix.
| A_up | 2D iterator corresponding to the upper_left element of the matrix A |
| A_bot | 2D iterator corresponding to one past-the-end bottom_right of the matrix A |
| L_up | 2D iterator corresponding to the upper_left element of the matrix L |
| L_bot | 2D iterator corresponding to one past-the-end bottom_right of the matrix L |
| LH_up | 2D iterator corresponding to the upper_left element of the matrix LH |
| LH_bot | 2D iterator corresponding to one past-the-end bottom_right of the matrix LH |
Definition at line 10008 of file linear_algebra.hpp.
|
inline |
cholesky decomposition of a square real symmetric and positive definite Matrix. 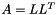 with L a lower triangular matrix. L is stored in the lower triangular part of A,
with L a lower triangular matrix. L is stored in the lower triangular part of A, 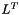 is stored in the upper triangular part of A.
is stored in the upper triangular part of A.
| A_up | 2D iterator corresponding to the upper_left element of the matrix A |
| A_bot | 2D iterator corresponding to one past-the-end bottom_right of the matrix A |
Definition at line 10093 of file linear_algebra.hpp.
|
inline |
cholesky decomposition of a square real symmetric positive definite Matrix. 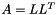 with L a lower triangular matrix
with L a lower triangular matrix
| A | 2D container. |
| L | 2D container. |
| LT | 2D container. |
Definition at line 10180 of file linear_algebra.hpp.
|
inline |
cholesky solve of system AX = B with A a square hermitian positive definite Matrix.
| A_up | 2D iterator corresponding to the upper_left element of the matrix A |
| A_bot | 2D iterator corresponding to one past-the-end bottom_right of the matrix A |
| X_first | RandomAccessIterator (points to the first element of X) |
| X_last | RandomAccessIterator (points to the one past the end element of X) |
| B_first | RandomAccessIterator (points to the first element of B) |
| B_last | RandomAccessIterator (points to the one past the end element of B) |
| precision | 1.0E-6 by default. |
Definition at line 10412 of file linear_algebra.hpp.
|
inline |
cholesky solve of system AX = B with A a square hermitian positive definite Matrix.
| A | 2D container. |
| X | 1D container. |
| B | 1D container. |
| precision | 1.0E-6 by default. |
Definition at line 10490 of file linear_algebra.hpp.
|
inline |
Computes the column norm ( 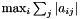 ) of a 2d range.
) of a 2d range.
| upper_left | RandomAccessIterator2d: first element of the 2d range. |
| bottom_right | RandomAccessIterator2d: one past-the-end of the 2d range. |
Definition at line 3214 of file linear_algebra.hpp.
|
inline |
Computes the column norm ( 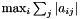 ) of a Container2d.
) of a Container2d.
| container | Container2d. |
Definition at line 3258 of file linear_algebra.hpp.
| bool slip::compareTwoRows2D | ( | double * | rowA, |
| double * | rowB | ||
| ) |
Comparator used to sort an Array2d.
| *rowA | Pointer to a 1st row. |
| *rowB | Pointer to a second row. |
Definition at line 2333 of file tecplot_binaries.hpp.
| bool slip::compareTwoRows3D | ( | double * | rowA, |
| double * | rowB | ||
| ) |
Comparator used to sort an Array2d.
| *rowA | Pointer to a 1st row. |
| *rowB | Pointer to a second row. |
Definition at line 1340 of file tecplot_binaries.hpp.
|
inline |
Computes the complex fft of a container.
| in_begin | A BidirectionalIterator to iterate throw the input data |
| in_end | A BidirectionalIterator at the end of the input data |
| out_begin | A BidirectionalIterator to iterate throw the output data |
|
inline |
Computes the complex fft2d of a container with 2d iterators.
| in_upper_left | |
| in_bottom_right | |
| out_upper_left |
|
inline |
Computes the complex fft2d of a container.
| datain | The input datas |
| dataout | The output datas |
|
inline |
Computes the complex fft3d of a container with 3d iterators.
| in_front_upper_left | |
| in_back_bottom_right | |
| out_front_upper_left |
|
inline |
Computes the complex fft3d of a container.
| datain | The input datas |
| dataout | The output datas |
|
inline |
Computes the complex fft4d of a container with 4d iterators.
| in_first_front_upper_left | |
| in_last_back_bottom_right | |
| out_first_front_upper_left |
|
inline |
Computes the complex fft4d of a container.
| datain | The input datas |
| dataout | The output datas |
|
inline |
Computes the standard complex crosscorrelation between two sequences using fft.
| first | An InputIterator. |
| last | An InputIterator. |
| first2 | An InputIterator. |
| last2 | An InputIterator. |
| result_first | An Output iterator. |
| result_last | An Output iterator. |
Definition at line 2473 of file correlation.hpp.
|
inline |
complex fftw of a container (from fftw3.h).
| in_begin | A BidirectionalIterator to iterate from the beginning of the input data |
| in_end | A BidirectionalIterator to iterate from the end of the input data |
| out_begin | A BidirectionalIterator to iterate from the beginning of the output data |
|
inline |
Computes the complex fftw2d of a container with 2d iterators.
| in_upper_left | |
| in_bottom_right | |
| out_upper_left |
|
inline |
Computes the complex fftw3d of a container with 3d iterators.
| in_front_upper_left | |
| in_back_bottom_right | |
| out_front_upper_left |
|
inline |
Computes the complex fftw3d of a container 3d.
|
inline |
Computes the complex fftw4d of a container with 4d iterators.
| in_first_front_upper_left | |
| in_last_back_bottom_right | |
| out_first_front_upper_left |
|
inline |
Computes the complex fftw4d of a container 4d.
|
inline |
Computes the complex Givens sinus and cosinus.
![\[ R = \left( \begin{array}{cc} \cos \theta & -\overline{\sin \theta} \\ \sin \theta & \cos \theta\\ \end{array}\right) \]](../../form_128.png)
![\[ \cos \theta = \frac{|xi|}{\epsilon\sqrt{xi\overline{xi}+xk\overline{xk}}} \]](../../form_129.png)
![\[ \sin \theta = \frac{-xk}{\epsilon sign(xi)\sqrt{xi\overline{xi}+xk\overline{xk}}} \]](../../form_130.png)
with
![\[ \epsilon = sign{\mathcal{R}(xi)} \]](../../form_131.png)
.
| xi | value at index i. |
| xk | value at index k. |
| sin | Givens sinus |
| cos | Givens cosinus. |
Definition at line 10761 of file linear_algebra.hpp.
|
inline |
Apply complex left Givens rotation multiplication.
Perform a left multiplication of a matrix M with the hermitian transpose Givens matrix on the row1 and row2 between the indices col1 and col2.
| M | the Container to multiply |
| row1 | the first row involved in the computation. |
| row2 | the second row involved in the computation. |
| sinus | Givens sinus. |
| cosinus | Givens cosinus. |
| col1 | the first column index. |
| col2 | the second column index. |
Definition at line 10885 of file linear_algebra.hpp.
|
inline |
Apply complex right Givens rotation multiplication.
Perform a right multiplication of a matrix M with the Givens matrix on the col1 and col2 between the indices row1 and row2.
| M | The Container to multiply |
| col1 | The first column involved in the computation. |
| col2 | The second column involved in the computation. |
| sinus | Givens sinus. |
| cosinus | Givens cosinus. |
| row1 | the first row index. |
| row2 | the second row index. |
Definition at line 10928 of file linear_algebra.hpp.
|
inline |
Computes the complex split radix fft of a container (from FFTPACK.hpp).
| in_begin | A BidirectionalIterator to iterate from the beginning of the input data |
| in_end | A BidirectionalIterator to iterate from the end of the input data |
| out_begin | A BidirectionalIterator to iterate from the beginning of the output data |
|
inline |
|
inline |
Computes the complex split-radix fft3d of a container with 3d iterators.
| in_front_upper_left | |
| in_back_bottom_right | |
| out_front_upper_left |
|
inline |
Computes the complex split-radix fft3d of a container 3d.
|
inline |
Computes the complex split-radix fft4d of a container with 4d iterators.
| in_first_front_upper_left | input start iterator4d |
| in_last_back_bottom_right | input end interator4d |
| out_first_front_upper_left | output start iterator4d |
|
inline |
Computes the complex split-radix fft4d of a container 4d.
|
inline |
Compose a file_name from the file name format basenamend*.ext.
| file_path_name | String of the file path name |
| img | Number to format. |
Definition at line 203 of file io_tools.hpp.
|
inline |
Definition at line 122 of file complex_cast.hpp.
|
inline |
Definition at line 123 of file complex_cast.hpp.
|
inline |
Definition at line 124 of file complex_cast.hpp.
|
inline |
Definition at line 125 of file complex_cast.hpp.
|
inline |
Definition at line 126 of file complex_cast.hpp.
|
inline |
Definition at line 127 of file complex_cast.hpp.
|
inline |
Definition at line 128 of file complex_cast.hpp.
|
inline |
Definition at line 129 of file complex_cast.hpp.
|
inline |
Definition at line 131 of file complex_cast.hpp.
|
inline |
Computes the conjugate of a matrix 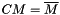 .
.
| M | Matrix container |
| CM | result of the conjugate |
Definition at line 2603 of file linear_algebra.hpp.
|
inline |
Computes the multiplication of a vector  by a scalar scal.
by a scalar scal.
| V_first | RandomAccessIterator to the first element of the Vector. |
| V_last | RandomAccessIterator to one-past-the-end element of the vector. |
| scal | A scalar value. |
| result_first | RandomAccessIterator to the first element of the result vector. |
Definition at line 774 of file linear_algebra.hpp.
|
inline |
Computes the multiplication of a vector 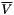 by a scalar scal.
by a scalar scal.
| V | The vector. |
| scal | A scalar value. |
| Result | Resulting vector. |
Definition at line 815 of file linear_algebra.hpp.
| void slip::container_cast | ( | Container & | cont, |
| _II & | first, | ||
| _II & | last | ||
| ) |
Get the default iterators of a SLIP container.
| cont | Container. |
| first | iterator to the first element of the container. |
| last | iterator to one past-the-end element of the container. |
Definition at line 205 of file container_cast.hpp.
| void slip::container_castR | ( | Container & | cont, |
| _II & | first, | ||
| _II & | last | ||
| ) |
Get the reverse default iterators of a SLIP container.
| cont | Container. |
| first | reverse iterator to the first element of the container. |
| last | reverse iterator to one past-the-end element of the container. |
Definition at line 402 of file container_cast.hpp.
| void slip::copy | ( | _II | first, |
| _II | last, | ||
| _OI | output_first | ||
| ) |
Copy algorithm optimized for slip iterators.
| first | A BidirectionalIterator. |
| last | A BidirectionalIterator. |
| output_first | A BidirectionalIterator. |
Definition at line 177 of file copy_ext.hpp.
|
related |
Definition at line 1454 of file KVector.hpp.
|
related |
Definition at line 2032 of file Vector.hpp.
|
related |
Definition at line 2045 of file Signal.hpp.
|
related |
Definition at line 3911 of file Matrix.hpp.
|
related |
Definition at line 5083 of file HyperVolume.hpp.
|
related |
Definition at line 5092 of file Matrix4d.hpp.
|
related |
Definition at line 5733 of file Matrix3d.hpp.
|
related |
Definition at line 6050 of file Volume.hpp.
|
related |
Definition at line 1584 of file KVector.hpp.
|
related |
Definition at line 2152 of file Vector.hpp.
|
related |
Definition at line 2165 of file Signal.hpp.
|
related |
Definition at line 4031 of file Matrix.hpp.
|
related |
Definition at line 5155 of file HyperVolume.hpp.
|
related |
Definition at line 5164 of file Matrix4d.hpp.
|
related |
Definition at line 5805 of file Matrix3d.hpp.
|
related |
Definition at line 6122 of file Volume.hpp.
|
inline |
Computes the covariance of a two sequences
![\[\frac{1}{n}\sum_i (x_i-\overline{x})(y_i-\overline{y})\]](../../form_201.png)
.
| first | An InputIterator. |
| last | An InputIterator. |
| first2 | An InputIterator. |
| mean1 | The mean of the first container. |
| mean2 | The mean of the second container. |
Definition at line 443 of file statistics.hpp.
|
inline |
Computes the covariance of a two sequences using a predicate on the first one
![\[\frac{1}{n}\sum_i (x_i-\overline{x})(y_i-\overline{y})\]](../../form_201.png)
.
| first | An InputIterator. |
| last | An InputIterator. |
| first2 | An InputIterator. |
| mean1 | The mean of the first range using the predicate. |
| mean2 | The mean of the second range using the predicate. |
| pred | a predicate function |
Definition at line 2768 of file statistics.hpp.
|
inline |
Computes the covariance of a two sequences over a mask
![\[\frac{1}{n}\sum_i (x_i-\overline{x})(y_i-\overline{y})\]](../../form_201.png)
.
| first | An InputIterator. |
| last | An InputIterator. |
| first2 | An InputIterator. |
| mask_first | An InputIterator on the mask |
| mean1 | The mean of the first range over the mask. |
| mean2 | The mean of the second range over the mask. |
| value | Mask value. |
Definition at line 1601 of file statistics.hpp.
|
inline |
Computes the crosscorrelation between two Images.
| in1_upper_left | : A 2d input iterator (image). |
| in1_bottom_right | : A 2d input iterator (image). |
| in2_upper_left | : A 2d input iterator (mask). |
| in2_bottom_right | : A 2d input iterator (mask). |
| out_upper_left | : A 2d output iterator (result). |
| out_bottom_right | : A 2d output iterator (result). |
| t | : type of algorithm CC, CCC, NCC, PNCC |
Definition at line 2012 of file correlation.hpp.
|
inline |
Computes the cumulative histogram from a histogram.
| histo_first | A RandomAccessIterator to the first element of the histogram. |
| histo_last | A RandomAccessIterator to the one past-the-end element of the histogram. |
| cum_histo_first | A RandomAccessIterator to the first element of the cumulative histogram. |
| cum_histo_last | A RandomAccessIterator to the one past-the-end element of the cumulative histogram. |
|
inline |
double-threshold algorithm
| first | begin InputIterator of the range to threshold |
| last | past-the-end InputIterator of the range to threshold |
| result | begin OutputIterator of the resulting range |
| min_t_value | minimum threshold value |
| max_t_value | maximum threshold value |
| false_value | result value when min_t_value <= *first <= max_t_value |
Definition at line 276 of file threshold.hpp.
|
inline |
Computes the Discrete Cosinus Transform II (forward) of a container.
| in_begin | A BidirectionalIterator to iterate from the beginning of the input data |
| in_end | A BidirectionalIterator to iterate from the end of the input data |
| out_begin | A BidirectionalIterator to iterate from the beginning of the output data |
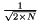
| int slip::decompose_direct | ( | const slip::Matrix< Type > & | M, |
| slip::Matrix< Type > & | K, | ||
| slip::Matrix< Type > & | R, | ||
| slip::Vector3d< Type > & | c | ||
| ) |
Direct-Decomposition a 3x4-Matrix into internal and external parameters.
| M | 3x4-Matrix |
| K | 3x3-Matrix containing the internal parameters |
| R | 3x3-Matrix containing the rotations |
| c | Vector3d containing the camera centre |
Definition at line 630 of file camera_algo.hpp.
| int slip::decompose_RQ | ( | const slip::Matrix< Type > & | M, |
| slip::Matrix< Type > & | K, | ||
| slip::Matrix< Type > & | R, | ||
| slip::Vector3d< Type > & | c | ||
| ) |
RQ-Decomposition 3x4-Matrix into internal and external parameters.
| M | 3x4-Matrix |
| K | 3x3-Matrix containing the internal parameters |
| R | 3x3-Matrix containing the rotations |
| c | Vector3d containing the camera centre |
Definition at line 582 of file camera_algo.hpp.
|
inline |
Computes 1d finite differences derivatives of an iterator range.
| first | A RandomAccessIterator. |
| last | A RandomAccessIterator. |
| der_ord | derivative order |
| sch_ord | order of derivation scheme |
| sch_shift | left shift value (upwind direction) |
| M | Precomputed finite differences coefficients Matrix. |
| result | A RandomAccessIterator. |
Definition at line 417 of file derivatives.hpp.
|
inline |
Computes 1d finite differences derivatives of an iterator range.
| first | A RandomAccessIterator to the first element of the data to derivate. |
| last | A RandomAccessIterator to the past-the-end element of the data to derivate. |
| der_ord | Derivative order. |
| sch_ord | Order of derivation scheme. |
| sch_shift | Left shift value (upwind direction). |
| kernels_first | std::vector which contain iterators to first elements of the derivative kernels |
| result | A RandomAccessIterator to the result container. |
Definition at line 512 of file derivatives.hpp.
|
inline |
Computes finite differences derivatives of a 2d range.
| I_up | upper_left iterator2d of the input 2d range |
| I_bot | bottom_right iterator2d of the input 2d range |
| grid_step | Grid step associated to the 2d range. |
| der_dir | SPATIAL_DIRECTION of the derivative:
|
| der_order | Derivative order. |
| sch_order | Order of derivation scheme. |
| R_up | upper_left iterator2d of the resulting 2d range |
| R_bot | bottom_right iterator2d of the resulting 2d range |
Definition at line 592 of file derivatives.hpp.
|
inline |
Computes finite differences derivatives of a 3d range.
| I_fup | upper_left iterator3d of the input 3d range |
| I_back_bot | bottom_right iterator3d of the input 3d range |
| grid_step | Grid step associated to the 3d range. |
| der_dir | SPATIAL_DIRECTION of the derivative:
|
| der_order | Derivative order. |
| sch_order | Order of derivation scheme. |
| R_fup | upper_left iterator3d of the resulting 3d range |
| R_back_bot | bottom_right iterator3d of the resulting 3d range |
Definition at line 696 of file derivatives.hpp.
|
inline |
Computes finite differences derivatives of a 4d range.
| I_ffup | upper_left iterator4d of the input 4d range |
| I_last_back_bot | bottom_right iterator4d of the input 4d range |
| grid_step | Grid step associated to the 4d range. |
| der_dir | 4D space direction of the derivative:
|
| der_order | Derivative order. |
| sch_order | Order of derivation scheme. |
| R_ffup | upper_left iterator4d of the resulting 4d range |
| R_last_back_bot | bottom_right iterator4d of the resulting 4d range |
Definition at line 880 of file derivatives.hpp.
|
inline |
Solve the linear system D*X=B when D a diagonal matrix
![\[ \left( \begin{array}{cccc} d_{1,1} & 0&\cdots&0\\ 0 & d_{2,2} & \ddots&\vdots\\ \vdots&\ddots&\ddots&0\\ 0&\cdots&0&d_{n,n}\\ \end{array}\right) \left( \begin{array}{c} x_{1}\\ x_{2}\\ \vdots\\ x_{n}\\ \end{array}\right) = \left( \begin{array}{c} b_{1}\\ b_{2}\\ \vdots\\ b_{n}\\ \end{array}\right) \]](../../form_95.png)
.
| first | RandomAccessIterator to the first element of D. |
| last | RandomAccessIterator to one-past-the-end element of D. |
| X_first | RandomAccessIterator to the first element of X. |
| X_last | RandomAccessIterator to one-past-the-end element of X. |
| B_first | RandomAccessIterator to the first element of B. |
| B_last | RandomAccessIterator to one-past-the-end element of B. |
| precision |
Definition at line 6716 of file linear_algebra.hpp.
| void slip::differential_operator | ( | RandomAccessIteratorNd1 | in_first, |
| RandomAccessIteratorNd1 | in_last, | ||
| RandomAccessIteratorNd2 | out_first, | ||
| Operator & | op | ||
| ) |
Applies a differential operator on a range.
| in_first | InputIterator. |
| in_last | InputIterator. |
| out_first | OutputIterator. |
| op | Differential operator. |
Definition at line 6255 of file derivatives.hpp.
| void slip::differential_operator_2 | ( | RandomAccessIteratorNd1 | in_first, |
| RandomAccessIteratorNd1 | in_last, | ||
| RandomAccessIteratorNd2 | out_first1, | ||
| RandomAccessIteratorNd3 | out_first2, | ||
| Operator1 & | op1, | ||
| Operator2 & | op2 | ||
| ) |
Applies 2 differential operators on a range.
| in_first | InputIterator. |
| in_last | InputIterator. |
| out_first1 | OutputIterator. |
| out_first2 | OutputIterator. |
| op1 | Differential operator. |
| op2 | Differential operator. |
Definition at line 6324 of file derivatives.hpp.
| void slip::differential_operator_3 | ( | RandomAccessIteratorNd1 | in_first, |
| RandomAccessIteratorNd1 | in_last, | ||
| RandomAccessIteratorNd2 | out_first1, | ||
| RandomAccessIteratorNd3 | out_first2, | ||
| RandomAccessIteratorNd4 | out_first3, | ||
| Operator1 & | op1, | ||
| Operator2 & | op2, | ||
| Operator3 & | op3 | ||
| ) |
Applies 3 differential operators on a range.
| in_first | InputIterator. |
| in_last | InputIterator. |
| out_first1 | OutputIterator. |
| out_first2 | OutputIterator. |
| out_first3 | OutputIterator. |
| op1 | Differential operator. |
| op2 | Differential operator. |
| op3 | Differential operator. |
Definition at line 6406 of file derivatives.hpp.
|
inline |
Computes the sum of the pointwise distances of two ranges: 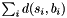 according to the distance d.
according to the distance d.
| first1 | An InputIterator. |
| last1 | An InputIterator. |
| first2 | An InputIterator. |
| distance | A binary functor. |
Definition at line 150 of file compare.hpp.
|
inline |
Computes the pointwise distances of two ranges: 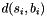 .
.
| first1 | An InputIterator. |
| last1 | An InputIterator. |
| first2 | An InputIterator. |
| result | An InputIterator. |
| distance | A binary functor. |
Definition at line 342 of file compare.hpp.
| Real slip::distance_if | ( | InputIterator1 | first1, |
| InputIterator1 | last1, | ||
| InputIterator2 | first2, | ||
| BinaryFunctor | distance, | ||
| Predicate | pred | ||
| ) |
Computes the sum of the pointwise distances of two ranges: 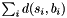 according to the distance d and the given predicate.
according to the distance d and the given predicate.
| first1 | An input iterator. |
| last1 | An input iterator. |
| first2 | An input iterator. |
| distance | A binary functor. |
| pred | A predicate. |
Definition at line 280 of file compare.hpp.
|
inline |
Computes the pointwise distances of two ranges: 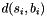 according to a Predicate.
according to a Predicate.
| first1 | An input iterator. |
| last1 | An input iterator. |
| first2 | An input iterator. |
| result | An output iterator. |
| distance | A binary operator. |
| pred | A predicate. |
Definition at line 468 of file compare.hpp.
|
inline |
Computes the sum of the pointwise distances of two ranges: 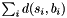 according to the distance d and the given mask range.
according to the distance d and the given mask range.
| first1 | An InputIterator. |
| last1 | An InputIterator. |
| first2 | An InputIterator. |
| distance | A binary functor. |
| mask_first | An input iterator. |
| value | true value of the mask range. Default is 1. |
Definition at line 211 of file compare.hpp.
|
inline |
Computes the pointwise distances of two ranges: 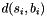 according to a given mask range.
according to a given mask range.
| first1 | An InputIterator. |
| last1 | An InputIterator. |
| mask_first | An InputIterator. |
| first2 | An InputIterator. |
| result | An InputIterator. |
| distance | A binary functor. |
| value | true value of the mask range. Default is 1. |
Definition at line 402 of file compare.hpp.
|
inline |
Computes the pointwise division of two ranges.
| __first1 | An InputIterator. |
| __last1 | An InputIterator. |
| __first2 | An InputIterator. |
| __result | An OutputIterator. |
Definition at line 701 of file arithmetic_op.hpp.
|
inline |
Computes the pointwise division of two ranges. according to a Predicate.
| __first1 | An input iterator. |
| __last1 | An input iterator. |
| __first2 | An input iterator. |
| __result | An output iterator. |
| __pred | A predicate. |
Definition at line 843 of file arithmetic_op.hpp.
|
inline |
Computes the pointwise division of two ranges according to a mask sequence.
| __first1 | An input iterator. |
| __last1 | An input iterator. |
| __mask_first | An input iterator. |
| __first2 | An input iterator. |
| __result | An output iterator. |
| value | true value of the mask range. Default is 1. |
Definition at line 777 of file arithmetic_op.hpp.
|
inline |
Divides a range by a scalar.
| __first1 | An InputIterator. |
| __last1 | An InputIterator. |
| scalar | A scalar value. |
| __result | An OutputIterator. |
Definition at line 1762 of file arithmetic_op.hpp.
|
inline |
Divides a range by a scalar according to a Predicate.
| __first1 | An input iterator. |
| __last1 | An input iterator. |
| scalar | A scalar value. |
| __result | An output iterator. |
| __pred | A predicate. |
Definition at line 1885 of file arithmetic_op.hpp.
|
inline |
Divides a range by a scalar according to a mask sequence.
| __first1 | An input iterator. |
| __last1 | An input iterator. |
| __mask_first | An input iterator. |
| scalar | A scalar value. |
| __result | An output iterator. |
| value | true value of the mask range. Default is 1. |
Definition at line 1827 of file arithmetic_op.hpp.
|
inline |
Eigen Values Computation for non symmetric matrix.
| A | Matrix container |
| E | Vector containing the real eigenvalue |
| sort | a boolean, if sort == true eigen will be sorted by decressing order |
Add the eigen vectors
optimize schur transform
Definition at line 204 of file linear_algebra_eigen.hpp.
| slip::lin_alg_traits<T>::value_type slip::epsilon | ( | ) |
Returns the epsilon value of a real or a complex.
Definition at line 211 of file linear_algebra_traits.hpp.
|
inline |
Computes the Euclidean norm 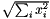 of a range.
of a range.
| first | An InputIterator. |
| last | An InputIterator. |
|
inline |
Computes the Euclidean norm 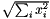 a range according to a Predicate.
a range according to a Predicate.
| first | An input iterator. |
| last | An input iterator. |
| pred | A predicate. |
|
inline |
Computes the Euclidean norm 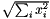 of a range according to a mask sequence.
of a range according to a mask sequence.
| first | An InputIterator. |
| last | An InputIterator. |
| mask_first | An input iterator. |
| value | true value of the mask range. Default is 1. |
|
inline |
Returns the evaluations of x until order n to the range [first,last) using the Chebyshev scheme.
The order of the resulting values is the following (1,x,2x^2-1,4x^3-3x,...).
| x | Location to be evaluated. |
| n | last order to compute. |
| first | RandomAccessIterator. |
| last | RandomAccessIterator. |
Definition at line 979 of file polynomial_algo.hpp.
|
inline |
Returns the evaluations of x until order n to the range [first,last) using the ChebyshevII scheme. The order of the resulting values is the following (1,2x,4x^2-1,8x^3-4x,...).
| x | Location to be evaluated. |
| n | last order to compute. |
| first | RandomAccessIterator. |
| last | RandomAccessIterator. |
Definition at line 331 of file polynomial_algo.hpp.
|
inline |
Returns the evaluations of x until order n to the range [first,last) using the Discrete Chebyshev scheme. The order of the resulting values is the following (1,2x-N+1,...).
| x | Location to be evaluated. |
| n | last order to compute. |
| first | RandomAccessIterator. |
| last | RandomAccessIterator. |
Definition at line 391 of file polynomial_algo.hpp.
|
inline |
Returns the evaluations of x until order n to the range [first,last) using the Hermite scheme. The order of the resulting values is the following (1,2x,4x^2-2,8x^3-12x,...).
| x | Location to be evaluated. |
| n | last order to compute. |
| first | RandomAccessIterator. |
| last | RandomAccessIterator. |
Definition at line 562 of file polynomial_algo.hpp.
|
inline |
Returns the evaluation of the polynomial given throw the range [first,last) at x using the horner scheme. The coefficients of the polynomial a0 + a1x + a2x^2 +... anx^n are supposed ordered as follows : (a0,a1,...,an).
| first | RandomAccessIterator. |
| last | RandomAccessIterator. |
| x | Location to be evaluated. |
Definition at line 787 of file polynomial_algo.hpp.
|
inline |
Returns the evaluations of x until order n to the range [first,last) using the Laguerre scheme. The order of the resulting values is the following (1,-x+1,0.5x^2-2x+1,-(1/6)x^3-(3/2)x^2-3x+1,...).
| x | Location to be evaluated. |
| n | last order to compute. |
| first | RandomAccessIterator. |
| last | RandomAccessIterator. |
Definition at line 738 of file polynomial_algo.hpp.
|
inline |
Returns the evaluations of x until order n to the range [first,last) using the legendre scheme.
The order of the resulting values is the following (1,x,0.5*(3x^2-1),...).
| x | Location to be evaluated. |
| n | last order to compute. |
| first | RandomAccessIterator. |
| last | RandomAccessIterator. |
Definition at line 926 of file polynomial_algo.hpp.
|
inline |
Returns the evaluation of the power of a slip::MultivariatePolynomial<T,DIM> P until order n to the range [first,last) using the horner scheme.
The order of the resulting values is the following (1,P,P^2,...,P^n).
| x | slip::MultivariatePolynomial<T,DIM> to be evaluated. |
| n | last order to compute. |
| first | RandomAccessIterator. |
| last | RandomAccessIterator. |
Definition at line 1179 of file polynomial_algo.hpp.
|
inline |
Returns the evaluation of the powers of slip::MultivariatePolynomial<T,DIM> 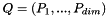 such that
such that 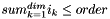 with
with 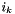 the power of the qk to the range [first,last) using the horner scheme.
the power of the qk to the range [first,last) using the horner scheme.
The order of the resulting values is the lexicographical one according to the powers of the monomial 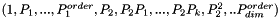 .
.
| x | to be evaluated. |
| order | Polynomial order to compute. |
| first | RandomAccessIterator. |
| last | RandomAccessIterator. |
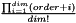
Definition at line 1255 of file polynomial_algo.hpp.
|
inline |
Returns the evaluation of the powers of X = (x1,x2) such that 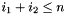 with
with  and
and 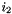 the power of x1 and x2. the range [first,last) using the horner scheme.
the power of x1 and x2. the range [first,last) using the horner scheme.
The order of the resulting values is the following (1,x1,...,x1^n,x2,x2x1,...,x2^2,..).
| x | Location (multivariate) to be evaluated. |
| n | Polynomial order to compute. |
| first | RandomAccessIterator. |
| last | RandomAccessIterator. |
Definition at line 1028 of file polynomial_algo.hpp.
|
inline |
Returns the evaluation of the power of x until order n to the range [first,last) using the horner scheme.
The order of the resulting values is the following (1,x,x^2,...,x^n).
| x | Location to be evaluated. |
| n | last order to compute. |
| first | RandomAccessIterator. |
| last | RandomAccessIterator. |
Definition at line 849 of file polynomial_algo.hpp.
|
inline |
Returns the evaluation of the powers of 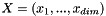 such that
such that 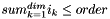 with
with 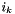 the power of the xk to the range [first,last) using the horner scheme.
the power of the xk to the range [first,last) using the horner scheme.
The order of the resulting values is the lexicographical one according to the powers of the monomial 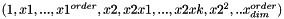 .
.
| x | Location (multivariate) to be evaluated. |
| order | Polynomial order to compute. |
| first | RandomAccessIterator. |
| last | RandomAccessIterator. |
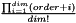
Definition at line 1073 of file polynomial_algo.hpp.
|
related |
Definition at line 1566 of file KVector.hpp.
|
related |
Definition at line 2134 of file Vector.hpp.
|
related |
Definition at line 2147 of file Signal.hpp.
|
related |
Definition at line 4013 of file Matrix.hpp.
|
related |
Definition at line 5137 of file HyperVolume.hpp.
|
related |
Definition at line 5146 of file Matrix4d.hpp.
|
related |
Definition at line 5787 of file Matrix3d.hpp.
|
related |
Definition at line 6104 of file Volume.hpp.
|
inline |
Definition at line 278 of file color_spaces.hpp.
|
inline |
Computes the FFT circular convolution.
| first | A RandomAccessIterator iterator to the data. |
| last | A RandomAccessIterator iterator to the data. |
| first2 | A RandomAccessIterator iterator to the filter. |
| last2 | A RandomAccessIterator iterator to the filter. |
| conv_first | A RandomAccessIterator iterator to the convolution. |
| conv_last | A RandomAccessIterator iterator to the convolution. |
Definition at line 652 of file convolution.hpp.
|
inline |
Computes the FFT circular crosscorrelation.
| first | A RandomAccessIterator iterator to the data. |
| last | A RandomAccessIterator iterator to the data. |
| first2 | A RandomAccessIterator iterator to the filter. |
| last2 | A RandomAccessIterator iterator to the filter. |
| result_first | A RandomAccessIterator iterator to the crosscorrelation. |
| result_last | A RandomAccessIterator iterator to the crosscorrelation. |
Definition at line 2397 of file correlation.hpp.
|
inline |
Computes the circular crosscorrelation between two 2D sequences using fft2d.
| in1_upper_left | A 2d input iterator (image). |
| in1_bottom_right | A 2d input iterator (image). |
| in2_upper_left | A 2d input iterator (mask). |
| in2_bottom_right | A 2d input iterator (mask). |
| out_upper_left | A 2d output iterator (result). |
| out_bottom_right | A 2d output iterator (result). |
Definition at line 2548 of file correlation.hpp.
|
inline |
Computes the standard crosscorrelation between two 3D sequences using fft3d.
| in1_front_upper_left | A 3d input iterator (volume). |
| in1_back_bottom_right | A 3d input iterator (volume). |
| in2_front_upper_left | A 3d input iterator (mask). |
| in2_back_bottom_right | A 3d input iterator (mask). |
| out_front_upper_left | A 3d output iterator (result). |
| out_back_bottom_right | A32d output iterator (result). |
Definition at line 2813 of file correlation.hpp.
|
inline |
Computes the FFT convolution.
| first | A RandomAccessIterator iterator to the data. |
| last | A RandomAccessIterator iterator to the data. |
| first2 | A RandomAccessIterator iterator to the filter. |
| last2 | A RandomAccessIterator iterator to the filter. |
| conv_first | A RandomAccessIterator iterator to the convolution. |
| conv_last | A RandomAccessIterator iterator to the convolution. |
Definition at line 710 of file convolution.hpp.
|
inline |
Computes the fft convolution of signal by a symmetric 1d-kernel.
| Signal | 1D Container of the input Signal. |
| Kernel | 1D Container of the kernel. |
| Result | 1D Container of the convolution result. |
Definition at line 773 of file convolution.hpp.
|
inline |
Computes the standard crosscorrelation between two 2D sequences using fft2d.
| in1_upper_left | : A 2d input iterator (image). |
| in1_bottom_right | : A 2d input iterator (image). |
| in2_upper_left | : A 2d input iterator (mask). |
| in2_bottom_right | : A 2d input iterator (mask). |
| out_upper_left | : A 2d output iterator (result). |
| out_bottom_right | : A 2d output iterator (result). |
Definition at line 2432 of file convolution.hpp.
|
inline |
Computes the convolution of a 2d signal using the fft2d.
| Signal | 2D Container of the input Signal. |
| Kernel | 2D Container of the kernel. |
| Result | 2D Container of the convolution result. |
Definition at line 2515 of file convolution.hpp.
|
inline |
Computes the convolution of two 3D sequences using fft3d.
| in1_front_upper_left | : A 3d input iterator (volume). |
| in1_back_bottom_right | : A 3d input iterator (volume). |
| in2_front_upper_left | : A 3d input iterator (mask). |
| in2_back_bottom_right | : A 3d input iterator (mask). |
| out_front_upper_left | : A 3d output iterator (result). |
| out_back_bottom_right | : A32d output iterator (result). |
Definition at line 3176 of file convolution.hpp.
|
inline |
Computes the convolution of a 3d signal using the fft3d.
| Signal | 3D Container of the input Signal. |
| Kernel | 3D Container of the kernel. |
| Result | 3D Container of the convolution result. |
Definition at line 3267 of file convolution.hpp.
|
inline |
Computes the convolution between two 3D sequences using fft3d.
| in1_front_upper_left | : A 3d input iterator (volume). |
| in1_back_bottom_right | : A 3d input iterator (volume). |
| in2_front_upper_left | : A 3d input iterator (mask). |
| in2_back_bottom_right | : A 3d input iterator (mask). |
| out_front_upper_left | : A 3d output iterator (result). |
| out_back_bottom_right | : A32d output iterator (result). |
Definition at line 3307 of file convolution.hpp.
|
inline |
Computes the standard crosscorrelation between two sequences using fft.
| first | An InputIterator. |
| last | An InputIterator. |
| first2 | An InputIterator. |
| result_first | An Output iterator. |
| result_last | An Output iterator. |
Definition at line 2250 of file correlation.hpp.
|
inline |
Computes the standard crosscorrelation between two 2D sequences using fft2d.
| in1_upper_left | A 2d input iterator (image). |
| in1_bottom_right | A 2d input iterator (image). |
| in2_upper_left | A 2d input iterator (mask). |
| in2_bottom_right | A 2d input iterator (mask). |
| out_upper_left | A 2d output iterator (result). |
| out_bottom_right | A 2d output iterator (result). |
Definition at line 2627 of file correlation.hpp.
|
inline |
Computes the standard crosscorrelation between two 2D sequences using fft2d.
| in1_upper_left | A 2d input iterator (image). |
| in1_bottom_right | A 2d input iterator (image). |
| in2_upper_left | A 2d input iterator (mask). |
| in2_bottom_right | A 2d input iterator (mask). |
| out_upper_left | A 2d output iterator (result). |
| out_bottom_right | A 2d output iterator (result). |
Definition at line 2718 of file correlation.hpp.
|
inline |
Computes the standard crosscorrelation between two 3D sequences using fft3d.
| in1_front_upper_left | A 3d input iterator (volume). |
| in1_back_bottom_right | A 3d input iterator (volume). |
| in2_front_upper_left | A 3d input iterator (mask). |
| in2_back_bottom_right | A 3d input iterator (mask). |
| out_front_upper_left | A 3d output iterator (result). |
| out_back_bottom_right | A 3d output iterator (result). |
Definition at line 2886 of file correlation.hpp.
|
inline |
Computes the standard crosscorrelation between two 3D sequences using fft3d.
| in1_front_upper_left | A 3d input iterator (volume). |
| in1_back_bottom_right | A 3d input iterator (volume). |
| in2_front_upper_left | A 3d input iterator (mask). |
| in2_back_bottom_right | A 3d input iterator (mask). |
| out_front_upper_left | A 3d output iterator (result). |
| out_back_bottom_right | A32d output iterator (result). |
Definition at line 2993 of file correlation.hpp.
|
inline |
Computes the FFT central part of the crosscorrelation.
| first | A RandomAccessIterator iterator to the data. |
| last | A RandomAccessIterator iterator to the data. |
| first2 | A RandomAccessIterator iterator to the filter. |
| last2 | A RandomAccessIterator iterator to the filter. |
| result_first | A RandomAccessIterator iterator to the correlation. |
| result_last | A RandomAccessIterator iterator to the correlation. |
Definition at line 2322 of file correlation.hpp.
|
inline |
Calculates the conjugates of the begin std::complex elements of a first container. Writes them at the end of a second container. This function is used to calculate the negative frequencies after a real fftw.
| begin1 | A ForwardIterator at the beginning of the input container |
| begin2 | A ForwardIterator at the beginning of the output container |
| end2 | A ForwardIterator at the end of the output container. |
|
inline |
Performs a duplicate of a 2D container, for use with the fft2d and ifft2d functions, in order to calculate the negative frequencies with the real fftw2d.
| upper_left | A ForwardIterator on std::complex numbers |
| bottom_right | A ForwardIterator on std::complex numbers |
|
inline |
|
inline |
Performs a shift of a 2d container, for use with the fft2d and ifft2d functions, in order to move the frequency 0 to the center of the container.
| upper_left | A ForwardIterator2D. |
| bottom_right | A ForwardIterator2D. 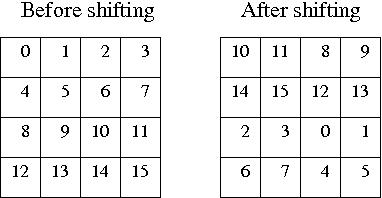
FFT shifting convention |
|
inline |
Performs a shift of a 2d container, for use with the fft2d and ifft2d functions, in order to move the frequency 0 to the center of the container.
| front_upper_left | A ForwardIterator3D. |
| back_bottom_right | A ForwardIterator3D. 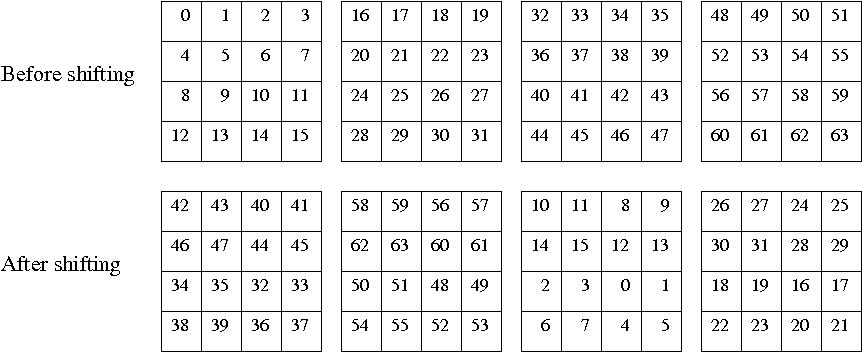
FFT shifting convention |
|
inline |
Performs a shift of a 4d container, for use with the fft4d and ifft4d functions, in order to move the frequency 0 to the center of the container.
| first_front_upper_left | A ForwardIterator4D. |
| last_back_bottom_right | A ForwardIterator4D. |
|
inline |
Computes the Discrete Cosinus Transform II (forward) of a container (from fftw).
| in_begin | A BidirectionalIterator to iterate from the beginning of the input data |
| in_end | A BidirectionalIterator to iterate from the end of the input data |
| out_begin | A BidirectionalIterator to iterate from the beginning of the output data |
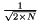
|
inline |
Computes the Discrete Cosinus Transform III (backward) of a container (from fftw).
| in_begin | A BidirectionalIterator to iterate from the beginning of the input data |
| in_end | A BidirectionalIterator to iterate from the end of the input data |
| out_begin | A BidirectionalIterator to iterate from the beginning of the output data |
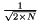
| void slip::fill_border | ( | _II | first, |
| _II | last, | ||
| std::size_t | b_size = 1, |
||
| const typename std::iterator_traits< _II >::value_type & | value = typename std::iterator_traits<_II>::value_type() |
||
| ) |
Fills the border of the range [first,last) with value.
| first | RandomAccessIterator or RandomAccessIterator2d or RandomAccessIterator3d. |
| last | RandomAccessIterator or RandomAccessIterator2d or RandomAccessIterator3d. |
| b_size | Size of the border (1 by default). |
| value | The value to fill the range (0 by default). |
Definition at line 440 of file border_treatment.hpp.
| void slip::fill_diagonal | ( | Container2d & | container, |
| const typename Container2d::value_type & | val, | ||
| const int | diag_number = 0 |
||
| ) |
Fill the diagonal diag_number of a 2d container with the value val.
| container | A 2d container |
| val | value |
| diag_number | number of the diagonal:
|
Definition at line 3503 of file linear_algebra.hpp.
| void slip::fill_diagonal | ( | MatrixIterator | M_up, |
| MatrixIterator | M_bot, | ||
| const typename MatrixIterator::value_type & | val, | ||
| const int | diag_number = 0 |
||
| ) |
Fill the diagonal diag_number of a 2d range with the value val.
| M_up | iterator2d to the upper_left element of the range. |
| M_bot | iterator2d to the bottom_right element og the range. |
| val | value |
| diag_number | number of the diagonal:
|
Definition at line 3556 of file linear_algebra.hpp.
|
inline |
return finite differences coefficients for derivation based on Taylor series (sch_ord-sch_shift steps upwind).
| sch_ord | Order of derivation scheme. |
| sch_shift | Left shift of derivation scheme. |
| Dinv | Container2D which will filled with Taylor series coefficients |
Definition at line 156 of file derivatives.hpp.
|
inline |
return finite differences coefficients for derivation based on Taylor series (sch_ord-sch_shift steps upwind)
| sch_ord | Order of derivation scheme. |
| sch_shift | Left shift of derivation scheme. |
| h | step of the grid. |
| Dinv | Container2D which will filled with Taylor series coefficients |
Definition at line 213 of file derivatives.hpp.
|
inline |
Computes finite differences kernels for derivation based on Taylor series (sch_ord-sch_shift steps upwind)
| der_ord | Order of the derivative. |
| sch_ord | Order of derivation scheme. |
| sch_shift | Left shift of derivation scheme. |
| kernels_first | std::vector which contains the begin iterators of the kernels. |
Definition at line 283 of file derivatives.hpp.
|
inline |
Computes finite differences kernels for derivation based on Taylor series (sch_ord-sch_shift steps upwind)
| der_ord | Order of the derivative. |
| sch_ord | Order of derivation scheme. |
| sch_shift | Left shift of derivation scheme. |
| kernels_first | std::vector which contains the begin iterators of the kernels. |
| h | grid step. |
Definition at line 341 of file derivatives.hpp.
|
inline |
Computes the first quartile value from a non sorted range.
| first | A RandomAccessIterator. |
| last | A RandomAccessIterator. |
Definition at line 1199 of file statistics.hpp.
|
inline |
Computes the first quartile value from a non sorted range using a predicate.
| first | A RandomAccessIterator. |
| last | A RandomAccessIterator. |
| pred | a predicate function |
Definition at line 3440 of file statistics.hpp.
|
inline |
Computes the first quartile value from a non sorted range over a mask.
| first | A RandomAccessIterator. |
| last | A RandomAccessIterator. |
| mask_first | An InputIterator of the mask |
| value | Mask value. |
Definition at line 2379 of file statistics.hpp.
|
inline |
Computes the Francis QR Step used in the Schur decomposition
![\[ H = Z \times H \times Z^{t}\]](../../form_157.png)
Algorithm 7.5-1 in "Matrix Computations", Golub and Van Loan.
| H | 2D container for the Input Hessenberg Matrix |
| Z | 2D container for the Z matrix |
| box | defines the part of the H matrix to be considered |
| compute_z | true if Z has to be computed |
Definition at line 750 of file linear_algebra_qr.hpp.
|
inline |
computes the Schur decomposition of a square Hessenberg Matrix and copy the eigenvalues in the Eig vector :
![\[ H = Z \times H \times Z^{t}\]](../../form_157.png)
Algorithm 7.5-2 in "Matrix Computations", Golub and Van Loan.
| H | 2D container for the Input Hessenberg Matrix |
| Eig | container for eigenvalues |
| Z | 2D container for the Z matrix |
| box | defines the part of H to be considered |
| precision | defines the precision of the iterations |
| compute_Z | true if Z has to be computed |
Definition at line 989 of file linear_algebra_qr.hpp.
|
inline |
Converts a 2-by-2 diagonal block of H in the Schur form, normalizes H and extract the associated eigenvalues.
![\[ H = Z \times H \times Z^{t}\]](../../form_157.png)
Algorithm 7.5-1 in "Matrix Computations", Golub and Van Loan.
| H | 2D container for the Input Hessenberg Matrix |
| Eig | container for eigenvalues |
| Z | 2D container for the Z matrix |
| b22 | 2_by_2 box that defines the diagonal block to be considered |
| compute_z | true if Z has to be computed |
Definition at line 850 of file linear_algebra_qr.hpp.
|
inline |
Computes the Frobenius norm ( 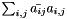 ) of a 2d range.
) of a 2d range.
| upper_left | RandomAccessIterator2d: first element of the 2d range. |
| bottom_right | RandomAccessIterator2d: one past-the-end of the 2d range. |
Definition at line 3286 of file linear_algebra.hpp.
|
inline |
Computes the Frobenius norm ( 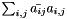 ) of a Container2d.
) of a Container2d.
| container | Container2d. |
Definition at line 3315 of file linear_algebra.hpp.
|
inline |
Computes the full convolution of signal by a 1d-kernel.
| first | A RandomAccessIterator. |
| last | A RandomAccessIterator. |
| kernel_first | A RandomAccessIterator. |
| kernel_last | A RandomAccessIterator. |
| result | A RandomAccessIterator. |
Definition at line 192 of file convolution.hpp.
|
inline |
Computes the full convolution of 2d signal by a 2d-kernel.
| S_up | A RandomAccessIterator2d. |
| S_bot | A RandomAccessIterator2d. |
| kernel_up | A RandomAccessIterator2d. |
| kernel_bot | A RandomAccessIterator2d. |
| R_up | A RandomAccessIterator2d. |
| R_bot | A RandomAccessIterator2d. |
Definition at line 2165 of file convolution.hpp.
|
inline |
Solve the linear system M*X=B using the Gauss elemination partial pivoting.
| M | 2D container |
| X | 1D container |
| B | 1D container |
| precision |
Definition at line 7566 of file linear_algebra.hpp.
|
inline |
Solve the linear system M*X=B with the Gauss pivot method, the null pivot are replaced by precision.
| M | 2D container |
| X | 1D container |
| B | 1D container |
| precision |
Definition at line 7687 of file linear_algebra.hpp.
|
inline |
Computes the generalized inner_product of two ranges:
![\[ (x,y)_A = \overline{x}^T A y = x^H A y \]](../../form_61.png)
.
| first1 | RandomAccessIterator to the first element of the vector x. |
| last1 | RandomAccessIterator to one-past-the-end element of the vector x. |
| A_upper_left | RandomAccessIterator2d to the upper_left matrix element. |
| A_bottom_right | RandomAccessIterator2d to the bottom_right matrix element. |
| first2 | RandomAccessIterator to the first element of the vector y. |
| last2 | RandomAccessIterator to one-past-the-end element of the vector y. |
| init | initial value (0 by default) |
Definition at line 442 of file linear_algebra.hpp.
|
inline |
Computes the generalized inner_product of two ranges:
![\[ (x,y)_A = \overline{x}^T A y = x^H A y \]](../../form_61.png)
.
| X | The vector x. |
| M | The matrix M. |
| Y | The vector y. |
Definition at line 509 of file linear_algebra.hpp.
|
inline |
Computes the generalized multiplication of a two Matrix:
![\[C = AB + C\]](../../form_70.png)
.
| A_up | 2D iterator on the upper_left element of A container |
| A_bot | 2D iterator on the bottom_right element of A container |
| B_up | 2D iterator on the upper_left element of B container |
| B_bot | 2D iterator on the bottom_right element of B container |
| C_up | 2D iterator on the upper_left element of C container |
| C_bot | 2D iterator on the bottom_right element of C container |
Definition at line 1741 of file linear_algebra.hpp.
|
inline |
Computes the generalized multiplication of a two Matrix:
![\[C = AB + C\]](../../form_70.png)
.
| A | The first Matrix container. |
| B | The second Matrix container. |
| C | The third input/output Matrix |
Definition at line 1811 of file linear_algebra.hpp.
|
inline |
Computes the generalised multiplication of a Matrix and a Vector: computes the update
![\[Y = MV + Y \]](../../form_68.png)
.
| M_up | RandomAccessIterator2d to the upper_left matrix element. |
| M_bot | RandomAccessIterator2d to the bottom_right matrix element. |
| V_first | RandomAccessIterator to the first element of the Vector V. |
| V_last | RandomAccessIterator to one-past-the-end element of the vector V. |
| Y_first | RandomAccessIterator to the first element of the Vector Y. |
| Y_last | RandomAccessIterator to one-past-the-end element of the vector Y. |
Definition at line 1510 of file linear_algebra.hpp.
|
inline |
Computes the generalised multiplication of a Matrix and a Vector: computes the update
![\[Y = MV + Y\]](../../form_69.png)
.
Definition at line 1574 of file linear_algebra.hpp.
| void slip::generic_plt_to_RegularVector2dField2d | ( | const std::string & | file_path_name, |
| RegularVector2dField2d & | reg, | ||
| std::string & | title, | ||
| std::string & | zonename, | ||
| std::vector< std::string > & | varnames, | ||
| const int | zone_loaded = 1 |
||
| ) |
Read a slip::RegularVector2dField2d from a binary tecplot file.
| file_path_name | String of the file path name. |
| reg | slip::RegularVector2dField2d container. |
| title | Title of the tecplot frame. |
| zone | Name of the tecplot zone. |
| varnames | Vector containing the variable names. |
| zone_loaded | Zone index to read (1 by default). |
Definition at line 2367 of file tecplot_binaries.hpp.
| void slip::generic_plt_to_RegularVector2dField2d | ( | const std::string & | file_path_name, |
| RegularVector2dField2d & | reg, | ||
| const int | zone_loaded = 1 |
||
| ) |
Read a slip::RegularVector2dField2d from a binary tecplot file.
| file_path_name | String of the file path name. |
| reg | slip::RegularVector2dField2d container. |
| zone_loaded | Zone index to read (1 by default). |
Definition at line 2513 of file tecplot_binaries.hpp.
| void slip::generic_plt_to_RegularVector3dField3d | ( | const std::string & | file_path_name, |
| RegularVector3dField3d & | reg, | ||
| std::string & | title, | ||
| std::string & | zonename, | ||
| std::vector< std::string > & | varnames, | ||
| const int | zone_loaded = 1 |
||
| ) |
Read a slip::RegularVector3dField3d from a binary tecplot file even if data are not properly sorted. This function is slower than plt_to_RegularVector3dField3d().
| file_path_name | String of the file path name. |
| reg | slip::RegularVector3dField3d container. |
| title | Title of the tecplot frame. |
| zonename | Name of the tecplot zone. |
| varnames | Name of all the variables. |
| zone_loaded | Zone index to read (1 by default). |
Definition at line 1374 of file tecplot_binaries.hpp.
| void slip::generic_plt_to_RegularVector3dField3d | ( | const std::string & | file_path_name, |
| RegularVector3dField3d & | reg, | ||
| const int | zone_loaded = 1 |
||
| ) |
Read a slip::RegularVector3dField3d from a binary tecplot file.
| file_path_name | String of the file path name. |
| reg | slip::RegularVector3dField3d container. |
| zone_loaded | Zone index to read (1 by default). |
Definition at line 1548 of file tecplot_binaries.hpp.
| void slip::get_diagonal | ( | const Container2d & | container, |
| RandomAccessIterator1 | diag_first, | ||
| RandomAccessIterator1 | diag_last, | ||
| const int | diag_number = 0 |
||
| ) |
Get the diagonal diag_number of a 2d container.
| container | A 2d container |
| diag_first | RandomAccessIterator to the first element of the diagonal. |
| diag_last | RandomAccessIterator to one past-the-end element of the diagonal. |
| diag_number | number of the diagonal:
|
Definition at line 3370 of file linear_algebra.hpp.
| int slip::get_tecplot_type | ( | ) |
Convert the type of a variable to an integer using Tecplot conventions.
| a | The variable to get the Tecplot type. |
Definition at line 112 of file tecplot_binaries.hpp.
| void slip::getpars_DLT | ( | const slip::Matrix< Type > & | P, |
| slip::Matrix< Type > & | Mat | ||
| ) |
Get calibration parameters using the DLT.
| P | Matrix containing the input data. |
| Mat | 3x4-Matrix containing the calibration parameters |
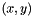 are the image coordinates,
are the image coordinates, 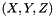 are the world coordinates.
are the world coordinates.
![\[ \begin{array}{ccccc} \cdots & \cdots & \cdots & \cdots & \cdots \\ x_i & y_i & X_i & Y_i & Z_i \\ \cdots & \cdots & \cdots & \cdots & \cdots \\ \end{array} \]](../../form_2.png)
Definition at line 187 of file camera_algo.hpp.
| void slip::getpars_DLT_norm | ( | const slip::Matrix< Type > & | P, |
| slip::Matrix< Type > & | Mat | ||
| ) |
Get calibration parameters using the DLT.
| P | Matrix containing the input data. |
| Mat | 3x4-Matrix containing the calibration parameters. |
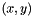 are the image coordinates,
are the image coordinates, 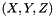 are the world coordinates.
are the world coordinates.
![\[ \begin{array}{ccccc} \cdots & \cdots & \cdots & \cdots & \cdots \\ x_i & y_i & X_i & Y_i & Z_i \\ \cdots & \cdots & \cdots & \cdots & \cdots \\ \end{array} \]](../../form_2.png)
Definition at line 262 of file camera_algo.hpp.
| void slip::getpars_Faugeras | ( | const slip::Matrix< Type > & | P, |
| slip::Matrix< Type > & | Mat | ||
| ) |
Get calibration parameters using the Faugeras-Algorithm.
| P | Matrix containing the input data. |
| Mat | 3x4-Matrix containing the calibration parameters |
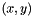 are the image coordinates,
are the image coordinates, 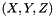 are the world coordinates.
are the world coordinates.
![\[ \begin{array}{ccccc} \cdots & \cdots & \cdots & \cdots & \cdots \\ x_i & y_i & X_i & Y_i & Z_i \\ \cdots & \cdots & \cdots & \cdots & \cdots \\ \end{array} \]](../../form_2.png)
Definition at line 297 of file camera_algo.hpp.
| void slip::getpars_SoloffUV | ( | const slip::Matrix< Type > & | P, |
| slip::MultivariatePolynomial< Type, 3 > & | Pol_x, | ||
| slip::MultivariatePolynomial< Type, 3 > & | Pol_y | ||
| ) |
Get calibration parameters using a polynomial fit (computation "by hand")
| P | Matrix containing the input data. |
| Pol_x | 1st MultivariatePolynomial containing the calibration parameters |
| Pol_y | 2nd MultivariatePolynomial containing the calibration parameters |
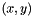 are the image coordinates,
are the image coordinates, 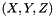 are the world coordinates.
are the world coordinates.
![\[ \begin{array}{ccccc} \cdots & \cdots & \cdots & \cdots & \cdots \\ x_i & y_i & X_i & Y_i & Z_i \\ \cdots & \cdots & \cdots & \cdots & \cdots \\ \end{array} \]](../../form_2.png)
Definition at line 413 of file camera_algo.hpp.
| void slip::getpars_SoloffXY | ( | const slip::Matrix< Type > & | P, |
| slip::MultivariatePolynomial< Type, 3 > & | Pol_x, | ||
| slip::MultivariatePolynomial< Type, 3 > & | Pol_y | ||
| ) |
Get calibration parameters using a polynomial fit (computation "by hand")
| P | Matrix containing the input data. |
| Pol_x | 1st MultivariatePolynomial containing the calibration parameters |
| Pol_y | 2nd MultivariatePolynomial containing the calibration parameters |
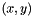 are the image coordinates,
are the image coordinates, 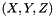 are the world coordinates.
are the world coordinates.
![\[ \begin{array}{ccccc} \cdots & \cdots & \cdots & \cdots & \cdots \\ x_i & y_i & X_i & Y_i & Z_i \\ \cdots & \cdots & \cdots & \cdots & \cdots \\ \end{array} \]](../../form_2.png)
Definition at line 501 of file camera_algo.hpp.
|
inline |
Computes the Givens sinus and cosinus.
![\[ R = \left( \begin{array}{cc} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta\\ \end{array}\right) \]](../../form_125.png)
![\[ \cos \theta = \frac{xi}{\sqrt{xi^2+xk^2}} \]](../../form_126.png)
![\[ \sin \theta = \frac{-xk}{\sqrt{xi^2+xk^2}} \]](../../form_127.png)
.
| xi | value at index i. |
| xk | value at index k. |
| sin | Givens sinus |
| cos | Givens cosinus. |
Definition at line 10720 of file linear_algebra.hpp.
| void slip::gram_matrix | ( | RandomAccessIterator | init_base_first, |
| RandomAccessIterator | init_base_end, | ||
| RandomAccessIterator2d | matrix_upper_left, | ||
| RandomAccessIterator2d | matrix_bottom_right, | ||
| InnerProduct | inner_prod | ||
| ) |
Compute the Gram matrix from a base.
| init_base_first | RandomAccessIterator to the first element of the Base to process. |
| init_base_end | RandomAccessIterator to one past the last element of the Base to process. |
| matrix_upper_left | RandomAccessIterator2d to the first element of the Gram matrix. |
| matrix_bottom_right | RandomAccessIterator2d to one past the last element of the Gram matrix. |
| inner_prod | BinaryFunction traducing the InnerProduct to use. |
Definition at line 521 of file gram_schmidt.hpp.
| void slip::gram_schmidt_normalization | ( | RandomAccessIterator | init_base_first, |
| RandomAccessIterator | init_base_end, | ||
| RandomAccessIterator | ortho_base_first, | ||
| RandomAccessIterator | ortho_base_end, | ||
| InnerProduct | inner_prod | ||
| ) |
Gram-Schmidt orthonormalization algorithm.
| init_base_first | RandomAccessIterator to the first element of the Base to process. |
| init_base_end | RandomAccessIterator to one past the last element of the Base to process. |
| ortho_base_first | RandomAccessIterator to the first element of the resulting Base. |
| ortho_base_end | RandomAccessIterator to one past the last element of the resulting Base. |
| inner_prod | BinaryFunction traducing the InnerProduct to use. |
Definition at line 125 of file gram_schmidt.hpp.
| void slip::gram_schmidt_orthogonalization | ( | RandomAccessIterator | init_base_first, |
| RandomAccessIterator | init_base_end, | ||
| RandomAccessIterator | ortho_base_first, | ||
| RandomAccessIterator | ortho_base_end, | ||
| InnerProduct | inner_prod | ||
| ) |
Gram-Schmidt orthogonalization algorithm.
| init_base_first | RandomAccessIterator to the first element of the Base to process. |
| init_base_end | RandomAccessIterator to one past the last element of the Base to process. |
| ortho_base_first | RandomAccessIterator to the first element of the resulting Base. |
| ortho_base_end | RandomAccessIterator to one past the last element of the resulting Base. |
| inner_prod | BinaryFunction traducing the InnerProduct to use. |
Definition at line 252 of file gram_schmidt.hpp.
|
inline |
(modified) Gram-Schmidt qr decomposition.
| A_up | 2D iterator on the upper_left element of A container |
| A_bot | 2D iterator on the bottom_right element of A container |
| Q_up | 2D iterator on the upper_left element of Q container |
| Q_bot | 2D iterator on the bottom_right element of Q container |
| R_up | 2D iterator on the upper_left element of R container |
| R_bot | 2D iterator on the bottom_right element of R container |
| tol | tolerance of the process |
Definition at line 211 of file linear_algebra_qr.hpp.
|
inline |
(modified) Gram-Schmidt qr decomposition.
| A | Input squared Matrix. |
| Q | Q matrix. |
| R | R matrix. |
| tol | tolerance of the process |
Definition at line 270 of file linear_algebra_qr.hpp.
|
inline |
Implements the three term recurrence relation for the Hermite multivariate polynomials, this function can be used to create a sequence of orthogonal polynomial, and for rising k. This recurrence relation holds for Hermite Polynomials:
![\[ P_{k+1}(x) = 2xP_k(x)-2kP_{k-1}(x)\]](../../form_239.png)
.
| k | The degree of the last polynomial calculated. |
| x | The x polynomial. |
| Pk | The value of the polynomial evaluated at degree k. |
| Pkm1 | The value of the polynomial evaluated at degree k-1. |
Definition at line 526 of file polynomial_algo.hpp.
|
inline |
Implements the three term recurrence relation for the Hermite polynomials, this function can be used to create a sequence of orthogonal polynomial, and for rising k. This recurrence relation holds for Hermite Polynomials:
![\[ P_{k+1}(x) = 2xP_k(x)-2kP_{k-1}(x)\]](../../form_239.png)
.
| k | The degree of the last polynomial calculated. |
| x | The x polynomial. |
| Pk | The value of the polynomial evaluated at degree k. |
| Pkm1 | The value of the polynomial evaluated at degree k-1. |
Definition at line 476 of file polynomial_algo.hpp.
|
inline |
Eigen Values Computation of an hermitian semi-definite positive matrix.
| A | Matrix container |
| EigenValues | Vector containing the real eigenvalue |
| EigenVectors | Container2d containing the eigenvectors |
Definition at line 124 of file linear_algebra_eigen.hpp.
|
inline |
Computes the hermitian inner-product of two ranges X and Y:
![\[ \overline{X}^TY = X^HY\]](../../form_60.png)
.
| first1 | iterator to the beginning of the first sequence (X) |
| last1 | iterator to the end of the first sequence (X) |
| first2 | iterator to the beginning of the second sequence (Y) |
| init | initial value. |
Definition at line 271 of file linear_algebra.hpp.
|
inline |
Computes the hermitian transpose of a matrix 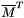 which is the transpose of the conjugate.
which is the transpose of the conjugate.
| M | Matrix container |
| TM | result of the transposition |
Definition at line 2476 of file linear_algebra.hpp.
|
inline |
Replaces A with the Hilbert matrix:
![\[h_{ij} = \frac{1}{i+j+1}\]](../../form_85.png)
.
| A | Matrix container |
Definition at line 3717 of file linear_algebra.hpp.
|
inline |
Simple histogram algorithm (uniform step)
| first | begin InputIterator of the container to histogram |
| last | past-the-end InputIterator of the container to histogram |
| histo_first | begin RandomAccessIterator of the histogram container |
| histo_last | past-the-end RandomAccessIterator of the histogram container |
| minval | Minimum value of the histogram |
| maxval | Maximum value of the histogram |
| step | Step of the histogram. Default value is 1. |
|
inline |
Simple histogram algorithm (uniform step) according to a predicate.
| first | begin InputIterator of the container to histogram |
| last | past-the-end InputIterator of the container to histogram |
| histo_first | begin RandomAccessIterator of the histogram container |
| histo_last | past-the-end RandomAccessIterator of the histogram container |
| pred | predicate function. |
| minval | Minimum value of the histogram |
| maxval | Maximum value of the histogram |
| step | Step of the histogram. Default value is 1. |
|
inline |
Simple histogram algorithm (uniform step) according to a mask sequence.
| first | begin InputIterator of the container to histogram |
| last | past-the-end InputIterator of the container to histogram |
| mask_first | An InputIterator on the mask |
| histo_first | begin RandomAccessIterator of the histogram container |
| histo_last | past-the-end RandomAccessIterator of the histogram container |
| minval | Minimum value of the histogram |
| maxval | Maximum value of the histogram |
| step | Step of the histogram. Default value is 1. |
| value | Mask value. |
|
inline |
Computes the hermitian left multiplication of a matrix:
![\[R = M1^H M2\]](../../form_66.png)
.
| M1_up | RandomAccessIterator2d to the upper_left matrix M1 element. |
| M1_bot | RandomAccessIterator2d to the bottom_right matrix M1 element. |
| M2_up | RandomAccessIterator2d to the upper_left matrix M2 element. |
| M2_bot | RandomAccessIterator2d to the bottom_right matrix M2 element. |
| result_up | RandomAccessIterator to the upper_left result matrix element. |
| result_up | RandomAccessIterator to the bottom_right result matrix element. |
Definition at line 1289 of file linear_algebra.hpp.
|
inline |
Computes the hermitian left multiplication of a matrix:
![\[R = M1^H M2\]](../../form_66.png)
.
| M1 | The first Matrix container. |
| M2 | The second Matrix container. |
| Result | The container which contains the result of the multiplication |
Definition at line 1359 of file linear_algebra.hpp.
|
inline |
Computes the hermitian matrix left multiplication of a vector:
![\[R = M^H V\]](../../form_67.png)
.
| M_up | RandomAccessIterator2d to the upper_left matrix element. |
| M_bot | RandomAccessIterator2d to the bottom_right matrix element. |
| V_first | RandomAccessIterator to the first element of the Vector. |
| V_last | RandomAccessIterator to one-past-the-end element of the vector. |
| R_first | RandomAccessIterator to the first element of the Vector R. |
| R_last | RandomAccessIterator to one-past-the-end element of the vector R. |
Definition at line 1403 of file linear_algebra.hpp.
|
inline |
Computes the hermitian matrix left multiplication of a vector:
![\[R = M^H V\]](../../form_67.png)
.
Definition at line 1460 of file linear_algebra.hpp.
|
inline |
Compute the Householder vector u of a vector a.
Given a vector a, compute the vector u of the matrix of Householder 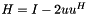 such that
such that 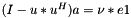 .
.
| a_begin | begin iterator of the vector to rotate |
| a_end | end iterator of the vector to rotate |
| u_begin | begin iterator of the householder vector |
| u_end | end iterator of the the householder vector |
| nu | 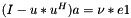 |
Definition at line 10981 of file linear_algebra.hpp.
|
inline |
Householder Hessenberg reduction of the square matrix M. The result is overwritten in M. The Hessenberg decomposition is 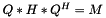 .
.
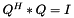
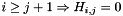
| M | 2D Container. |
Definition at line 11212 of file linear_algebra.hpp.
|
inline |
Householder Hessenberg reduction of the square matrix M. The Hessenberg decomposition is 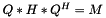 .
.
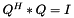
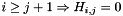
| M | 2D Container of the input Matrix. |
| H | 2D Container of the Hessenberg matrix. |
Definition at line 11279 of file linear_algebra.hpp.
|
inline |
Householder Hessenberg reduction of the square matrix M. The Hessenberg decomposition is 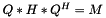 .
.
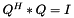
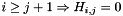
| M | 2D Container of the input Matrix. |
| H | 2D Container of the Hessenberg matrix. |
| Q | 2D Container of the Q matrix. |
Definition at line 11337 of file linear_algebra.hpp.
|
inline |
in place Householder QR decomposition M = QR
![\[ M = Q \times R \]](../../form_142.png)
![\[ Q \times Q^{t} = I \]](../../form_143.png)
Q is a rotation matrix and R is an upper triangular matrix
| M | 2D Container. |
| V0 | Vector which contains the first value of householder vectors |
Definition at line 301 of file linear_algebra_qr.hpp.
|
inline |
Computes the QR decomposition of a matrix M :
![\[ M = Q \times R \]](../../form_142.png)
![\[ Q \times Q^{t} = I \]](../../form_143.png)
Q is a rotation matrix and R is an upper triangular matrix.
| M | 2D container for M |
| Q | 2D container for Q |
| R | 2D container for R |
Definition at line 378 of file linear_algebra_qr.hpp.
|
inline |
Computes the hermitian left multiplication:
![\[R = V^H M\]](../../form_64.png)
.
| V_first | RandomAccessIterator to the first element of the Vector. |
| V_last | RandomAccessIterator to one-past-the-end element of the vector. |
| M_up | RandomAccessIterator2d to the upper_left matrix element. |
| M_bot | RandomAccessIterator2d to the bottom_right matrix element. |
| result_first | RandomAccessIterator to the first element of the Vector R. |
| result_last | RandomAccessIterator to one-past-the-end element of the vector R. |
Definition at line 1078 of file linear_algebra.hpp.
|
inline |
Computes the hermitian left multiplication:
![\[R = V^H M\]](../../form_64.png)
.
Definition at line 1143 of file linear_algebra.hpp.
|
inline |
Computes the Discrete Cosinus Transform III (backward) of a container.
| in_begin | A BidirectionalIterator to iterate from the beginning of the input data |
| in_end | A BidirectionalIterator to iterate from the end of the input data |
| out_begin | A BidirectionalIterator to iterate from the beginning of the output data |
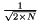
|
inline |
Returns an identity matrix which dimensions are nr*nc.
| nr | Number of rows. |
| nc | Number of columns. |
Definition at line 3608 of file linear_algebra.hpp.
|
inline |
Set a 2d range to the identity matrix.
| A_up | |
| A_bot |
Definition at line 3639 of file linear_algebra.hpp.
|
inline |
Replaces A with the identity matrix.
| A | Matrix container |
Definition at line 3672 of file linear_algebra.hpp.
|
inline |
Computes the inverse fft of a container.
| in_begin | A BidirectionalIterator to iterate throw the input data |
| in_end | A BidirectionalIterator at the end of the input data |
| out_begin | A BidirectionalIterator to iterate throw the output data |
|
inline |
Computes the ifft2d of a container with 2d iterators.
| in_upper_left | |
| in_bottom_right | |
| out_upper_left |
|
inline |
Computes the fft2d of a container.
| datain | The input datas |
| dataout | The output datas |
|
inline |
Computes the ifft3d of a container with 3d iterators.
| in_front_upper_left | |
| in_back_bottom_right | |
| out_front_upper_left |
|
inline |
Computes the fft3d of a container.
| datain | The input datas |
| dataout | The output datas |
|
inline |
Computes the ifft4d of a container with 4d iterators.
| in_first_front_upper_left | |
| in_last_back_bottom_right | |
| out_first_front_upper_left |
|
inline |
Computes the fft4d of a container.
| datain | The input datas |
| dataout | The output datas |
|
inline |
Computes the fftw backward of a container (from fftw3.h).
| in_begin | A BidirectionalIterator to iterate from the beginning of the input data |
| in_end | A BidirectionalIterator to iterate from the end of the input data |
| out_begin | A BidirectionalIterator to iterate from the beginning of the output data |
|
inline |
Computes the ifftw2d of a container with 2d iterators.
| in_upper_left | |
| in_bottom_right | |
| out_upper_left |
|
inline |
Computes the ifftw2d of a container.
| datain | The input datas |
| dataout | The output datas |
|
inline |
Computes the ifftw3d of a container with 3d iterators.
| in_front_upper_left | |
| in_back_bottom_right | |
| out_front_upper_left |
|
inline |
Computes the ifftw3d of a container 3d.
| datain | The input datas |
| dataout | The output datas |
|
inline |
Computes the ifftw4d of a container with 4d iterators.
| in_first_front_upper_left | |
| in_last_back_bottom_right | |
| out_first_front_upper_left |
|
inline |
Computes the ifftw4d of a container 4d.
| datain | The input datas |
| dataout | The output datas |
|
inline |
Extract the imaginary Matrix of a complex Matrix. 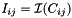 .
.
| C | Complex Matrix container |
| I | result of the imag |
Definition at line 2684 of file linear_algebra.hpp.
|
inline |
Computes the infinite norm 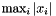 of a range.
of a range.
| first | An InputIterator. |
| last | An InputIterator. |
| Value_T slip::infinite_norm_if | ( | InputIterator | first, |
| InputIterator | last, | ||
| Predicate | pred | ||
| ) |
Computes the infinite norm 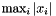 a range according to a Predicate.
a range according to a Predicate.
| first | An input iterator. |
| last | An input iterator. |
| pred | A predicate. |
|
inline |
Computes the infinite norm 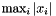 of a range according to a mask sequence.
of a range according to a mask sequence.
| first | An InputIterator. |
| last | An InputIterator. |
| mask_first | An input iterator. |
| value | true value of the mask range. Default is 1. |
|
inline |
Computes the inner_product of two ranges X and Y:
![\[ \overline{X}^TY = X^HY\]](../../form_60.png)
.
| first1 | iterator to the beginning of the first sequence (X) |
| last1 | iterator to the end of the first sequence (X) |
| first2 | iterator to the beginning of the second sequence (Y) |
| init | initial value (zero by default). |
Definition at line 323 of file linear_algebra.hpp.
|
inline |
Computes the inner_product of two ranges X and Y:
![\[ \overline{X}^TY = X^HY\]](../../form_60.png)
.
Definition at line 381 of file linear_algebra.hpp.
| _Tp slip::inner_product_if | ( | _InputIterator1 | first1, |
| _InputIterator1 | last1, | ||
| _InputIterator2 | first2, | ||
| _Tp | init, | ||
| _Predicate | pred | ||
| ) |
Compute inner product of two ranges according to a Predicate.
| first1 | Start of range 1. |
| last1 | End of range 1. |
| first2 | Start of range 2. |
| init | Starting value to add other values to. |
| pred | Predicate. |
Definition at line 275 of file stl_numeric_ext.hpp.
| _Tp slip::inner_product_if | ( | _InputIterator1 | first1, |
| _InputIterator1 | last1, | ||
| _InputIterator2 | first2, | ||
| _Tp | init, | ||
| _BinaryOperation1 | binary_op1, | ||
| _BinaryOperation2 | binary_op2, | ||
| _Predicate | pred | ||
| ) |
Compute inner product of two ranges according to a Predicate.
| first1 | Start of range 1. |
| last1 | End of range 1. |
| first2 | Start of range 2. |
| init | Starting value to add other values to. |
| binary_op1 | Function object to accumulate with. |
| binary_op2 | Function object to apply to pairs of input values. |
| pred | Predicate. |
Definition at line 341 of file stl_numeric_ext.hpp.
| _Tp slip::inner_product_mask | ( | _InputIterator1 | first1, |
| _InputIterator1 | last1, | ||
| _MaskIterator | mask_first, | ||
| _InputIterator2 | first2, | ||
| _Tp | init, | ||
| typename std::iterator_traits< _MaskIterator >::value_type | value = typename std::iterator_traits<_MaskIterator>::value_type(1) |
||
| ) |
Compute inner product of two ranges according to a mask range.
| first1 | Start of range 1. |
| last1 | End of range 1. |
| mask_first | Start of the mask range. |
| first2 | Start of range 2. |
| init | Starting value to add other values to. |
| value | true value of the mask range. Default is 1. |
Definition at line 128 of file stl_numeric_ext.hpp.
| _Tp slip::inner_product_mask | ( | _InputIterator1 | first1, |
| _InputIterator1 | last1, | ||
| _MaskIterator | mask_first, | ||
| _InputIterator2 | first2, | ||
| _Tp | init, | ||
| _BinaryOperation1 | binary_op1, | ||
| _BinaryOperation2 | binary_op2, | ||
| typename std::iterator_traits< _MaskIterator >::value_type | value = typename std::iterator_traits<_MaskIterator>::value_type(1) |
||
| ) |
Compute inner product of two ranges according to a mask range.
| first1 | Start of range 1. |
| last1 | End of range 1. |
| mask_first | Start of the mask range. |
| first2 | Start of range 2. |
| init | Starting value to add other values to. |
| binary_op1 | Function object to accumulate with. |
| binary_op2 | Function object to apply to pairs of input values. |
| value | true value of the mask range. Default is 1. |
Definition at line 207 of file stl_numeric_ext.hpp.
|
inline |
Computes the inverse of a matrix using gaussian elimination.
| M | Matrix container |
| nr1 | The number of rows of M |
| nc1 | The number of columns of M |
| IM | result of the inversion |
| nr2 | The number of rows of IM |
| nc2 | The number of columns of IM |
Definition at line 4963 of file linear_algebra.hpp.
|
inline |
Computes the inverse of a matrix using gaussian elimination.
| M | Matrix container |
| IM | result of the inversion |
Definition at line 5083 of file linear_algebra.hpp.
| slip::Point2d<Type> slip::invert_distortion_model | ( | const slip::Point2d< Type > & | pd, |
| const slip::Vector< Type > & | p | ||
| ) |
Inverts distortion model using the Newton-method.
| pd | slip::Point2d (distorted camera coordinates) |
| p | Vector containing all camera parameters (size of 23) |
Definition at line 696 of file camera_algo.hpp.
|
inline |
Iota assigns sequential increasing values based on a predefined step to a range. That is, it assigns value to *first, value + step to *(first + 1) and so on. In general, each iterator i in the range [first,last) is assigned value + step * (i - first).
| first | An InputIterator. |
| last | An InputIterator. |
| value | Init value. |
| step | Step between two values. Default step is 1. |
Definition at line 2087 of file arithmetic_op.hpp.
|
inline |
Iota_mask sequential increasing values based on a predefined step to a range according to a mask sequence.
| first | An InputIterator. |
| last | An InputIterator. |
| mask_first | An input iterator. |
| value | Init value. |
| step | Step between two values. Default step is 1. |
| value_mask | "True" value of the mask. Default is 1. |
Definition at line 2131 of file arithmetic_op.hpp.
|
inline |
Test if a matrix is a band matrix.
| A_up | 2D iterator on the upper_left element of A container |
| A_bot | 2D iterator on the bottom_right element of A container |
| lower_band_width | Lower band width. |
| upper_band_width | Upper band width. |
| tol |
Definition at line 4266 of file linear_algebra.hpp.
|
inline |
Test if a matrix is symmetric.
| A | Matrix container |
| lower_band_width | Lower band width. |
| upper_band_width | Upper band width. |
| tol |
Definition at line 4333 of file linear_algebra.hpp.
| bool slip::is_complex | ( | const T & | val | ) |
Test if an element is complex.
| val. | Value to evaluate. |
Definition at line 179 of file linear_algebra_traits.hpp.
|
inline |
Test if a matrix is diagonal.
| A_up | 2D iterator on the upper_left element of A container |
| A_bot | 2D iterator on the bottom_right element of A container |
| tol | Tolerance (epsilon by default). |
Definition at line 3899 of file linear_algebra.hpp.
|
inline |
Test if a matrix is diagonal.
| A | Matrix container |
| tol | Tolerance (epsilon by default). |
Definition at line 3952 of file linear_algebra.hpp.
|
inline |
Test if a matrix is hermitian.
| A_up | 2D iterator on the upper_left element of A container |
| A_bot | 2D iterator on the bottom_right element of A container |
| tol | Tolerance (epsilon by default). |
Definition at line 3986 of file linear_algebra.hpp.
|
inline |
Test if a matrix is hermitian.
| A | Matrix container |
| tol | Tolerance (epsilon by default). |
Definition at line 4040 of file linear_algebra.hpp.
|
inline |
Test if a matrix is identity.
| A | Matrix container |
| tol | Tolerance (epsilon by default). |
Definition at line 3848 of file linear_algebra.hpp.
|
inline |
Test if a matrix is lower_bidiagonal.
| A_up | 2D iterator on the upper_left element of A container |
| A_bot | 2D iterator on the bottom_right element of A container |
| tol | Tolerance (epsilon by default). |
Definition at line 4470 of file linear_algebra.hpp.
|
inline |
Test if a matrix is lower bidiagonal.
| A | Matrix container |
| tol | Tolerance (epsilon by default). |
Definition at line 4495 of file linear_algebra.hpp.
|
inline |
Test if a matrix is lower_hessenberg.
| A_up | 2D iterator on the upper_left element of A container |
| A_bot | 2D iterator on the bottom_right element of A container |
| tol | Tolerance (epsilon by default). |
Definition at line 4575 of file linear_algebra.hpp.
|
inline |
Test if a matrix is lower hessenber.
| A | Matrix container |
| tol | Tolerance (epsilon by default). |
Definition at line 4601 of file linear_algebra.hpp.
|
inline |
Test if a matrix is lower_triangular.
| A_up | 2D iterator on the upper_left element of A container |
| A_bot | 2D iterator on the bottom_right element of A container |
| tol | Tolerance (epsilon by default). |
Definition at line 4679 of file linear_algebra.hpp.
|
inline |
Test if a matrix is lower triangular.
| A | Matrix container |
| tol | Tolerance (epsilon by default). |
Definition at line 4703 of file linear_algebra.hpp.
|
inline |
Test if a matrix has a nul diagonal.
| A_up | 2D iterator on the upper_left element of A container. |
| A_bot | 2D iterator on the bottom_right element of A container. |
| diag_number | digonal number. |
| tol | Tolerance (epsilon by default). |
Definition at line 4730 of file linear_algebra.hpp.
| bool slip::is_real | ( | const T & | val | ) |
Test if an element is real.
| val. | Value to evaluate. |
Definition at line 128 of file linear_algebra_traits.hpp.
|
inline |
Test if a matrix is skew hermitian.
| A_up | 2D iterator on the upper_left element of A container |
| A_bot | 2D iterator on the bottom_right element of A container |
| tol | Tolerance (epsilon by default). |
Definition at line 4084 of file linear_algebra.hpp.
|
inline |
Test if a matrix is skew hermitian.
| A | Matrix container |
| tol | Tolerance (epsilon by default). |
Definition at line 4150 of file linear_algebra.hpp.
|
inline |
Test if a matrix is squared.
| A | Matrix container |
Definition at line 3800 of file linear_algebra.hpp.
|
inline |
Test if a matrix is squared.
| A_up | 2D iterator on the upper_left element of A container |
| A_bot | 2D iterator on the bottom_right element of A container |
Definition at line 3823 of file linear_algebra.hpp.
|
inline |
Test if a matrix is symmetric.
| A_up | 2D iterator on the upper_left element of A container |
| A_bot | 2D iterator on the bottom_right element of A container |
| tol | Tolerance (epsilon by default). |
Definition at line 4189 of file linear_algebra.hpp.
|
inline |
Test if a matrix is symmetric.
| A | Matrix container |
| tol | Tolerance (epsilon by default). |
Definition at line 4229 of file linear_algebra.hpp.
|
inline |
Test if a matrix is tridiagonal.
| A_up | 2D iterator on the upper_left element of A container |
| A_bot | 2D iterator on the bottom_right element of A container |
| tol |
Definition at line 4364 of file linear_algebra.hpp.
|
inline |
Test if a matrix is tridiagonal.
| A | Matrix container |
| tol |
Definition at line 4390 of file linear_algebra.hpp.
|
inline |
Test if a matrix is upper_bidiagonal.
| A_up | 2D iterator on the upper_left element of A container |
| A_bot | 2D iterator on the bottom_right element of A container |
| tol |
Definition at line 4418 of file linear_algebra.hpp.
|
inline |
Test if a matrix is upper bidiagonal.
| A | Matrix container |
| tol | Tolerance (epsilon by default). |
Definition at line 4442 of file linear_algebra.hpp.
|
inline |
Test if a matrix is upper_hessenberg.
| A_up | 2D iterator on the upper_left element of A container |
| A_bot | 2D iterator on the bottom_right element of A container |
| tol | Tolerance (epsilon by default). |
Definition at line 4521 of file linear_algebra.hpp.
|
inline |
Test if a matrix is upper hessenber.
| A | Matrix container |
| tol | Tolerance (epsilon by default). |
Definition at line 4547 of file linear_algebra.hpp.
|
inline |
Test if a matrix is upper_triangular.
| A_up | 2D iterator on the upper_left element of A container |
| A_bot | 2D iterator on the bottom_right element of A container |
| tol | Tolerance (epsilon by default). |
Definition at line 4628 of file linear_algebra.hpp.
|
inline |
Test if a matrix is upper triangular.
| A | Matrix container |
| tol | Tolerance (epsilon by default). |
Definition at line 4653 of file linear_algebra.hpp.
|
inline |
Computes the Kullback-Leibler "distance" of two ranges : 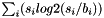 .
.
| first1 | An InputIterator. |
| last1 | An InputIterator. |
| first2 | An InputIterator. |
Definition at line 1780 of file compare.hpp.
|
inline |
Computes the Kullback-Leibler "distance" of two ranges according to a Predicate.
| first1 | An input iterator. |
| last1 | An input iterator. |
| first2 | An input iterator. |
| pred | A predicate. |
Definition at line 1878 of file compare.hpp.
|
inline |
Computes the Kullback-Leibler "distance" of two ranges according to a mask sequence : 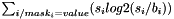 .
.
| first1 | An InputIterator. |
| last1 | An InputIterator. |
| mask_first | An input iterator. |
| first2 | An InputIterator. |
| value | true value of the mask range. Default is 1. |
Definition at line 1823 of file compare.hpp.
|
inline |
Computes the kurtosis of a range
![\[\frac{n \sum_i (x_i-\overline{x})^4}{\left(\sum_i (x_i-\overline{x})^2\right)^2}\]](../../form_207.png)
A high kurtosis distribution has a sharper peak and longer, fatter tails, while a low kurtosis distribution has a more rounded peak and shorter thinner tails. Here are some common value of kurtosis for unimodal and symmetric densities:
| first | An InputIterator. |
| last | An InputIterator. |
| mean | The mean of the container itself. |
Definition at line 666 of file statistics.hpp.
|
inline |
Computes the kurtosis of a range using a predicate
![\[\frac{n \sum_i (x_i-\overline{x})^4}{\left(\sum_i (x_i-\overline{x})^2\right)^2}\]](../../form_207.png)
A high kurtosis distribution has a sharper peak and longer, fatter tails, while a low kurtosis distribution has a more rounded peak and shorter thinner tails. Here are some common value of kurtosis for unimodal and symmetric densities:
| first | An InputIterator. |
| last | An InputIterator. |
| mean | The mean of the range itself using the predicate. |
| pred | a predicate function |
Definition at line 3061 of file statistics.hpp.
|
inline |
Computes the kurtosis of a range over a mask
![\[\frac{n \sum_i (x_i-\overline{x})^4}{\left(\sum_i (x_i-\overline{x})^2\right)^2}\]](../../form_207.png)
A high kurtosis distribution has a sharper peak and longer, fatter tails, while a low kurtosis distribution has a more rounded peak and shorter thinner tails. Here are some common value of kurtosis for unimodal and symmetric densities:
| first | An InputIterator. |
| last | An InputIterator. |
| mask_first | An InputIterator on the mask |
| mean | The mean of the range itself over the mask. |
| value | Mask value. |
Definition at line 1907 of file statistics.hpp.
|
inline |
Computes the L1 distance of two ranges : 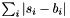 .
.
| first1 | An InputIterator. |
| last1 | An InputIterator. |
| first2 | An InputIterator. |
Definition at line 1313 of file compare.hpp.
| Real slip::L1_distance_if | ( | InputIterator1 | first1, |
| InputIterator1 | last1, | ||
| InputIterator2 | first2, | ||
| Predicate | pred | ||
| ) |
Computes the L1 distance of two ranges according to a Predicate.
| first1 | An input iterator. |
| last1 | An input iterator. |
| first2 | An input iterator. |
| pred | A predicate. |
Definition at line 1412 of file compare.hpp.
|
inline |
Computes the L1 distance of two ranges according to a mask sequence : 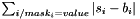 .
.
| first1 | An InputIterator. |
| last1 | An InputIterator. |
| mask_first | An input iterator. |
| first2 | An InputIterator. |
| value | true value of the mask range. Default is 1. |
Definition at line 1355 of file compare.hpp.
|
inline |
Computes the L1 norm 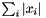 of a range.
of a range.
| first | An InputIterator. |
| last | An InputIterator. |
| Value_T slip::L1_norm_if | ( | InputIterator | first, |
| InputIterator | last, | ||
| Predicate | pred | ||
| ) |
Computes the L1 norm 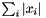 a range according to a Predicate.
a range according to a Predicate.
| first | An input iterator. |
| last | An input iterator. |
| pred | A predicate. |
|
inline |
Computes the L1 norm 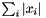 of a range according to a mask sequence.
of a range according to a mask sequence.
| first | An InputIterator. |
| last | An InputIterator. |
| mask_first | An input iterator. |
| value | true value of the mask range. Default is 1. |
|
inline |
Computes the square euclidian distance of two ranges: 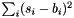 .
.
| first1 | An InputIterator. |
| last1 | An InputIterator. |
| first2 | An InputIterator. |
Definition at line 1059 of file compare.hpp.
| Real slip::L22_distance_if | ( | InputIterator1 | first1, |
| InputIterator1 | last1, | ||
| InputIterator2 | first2, | ||
| Predicate | pred | ||
| ) |
Computes the square eucludian distance of two ranges according to a Predicate.
| first1 | An input iterator. |
| last1 | An input iterator. |
| first2 | An input iterator. |
| pred | A predicate. |
Definition at line 1156 of file compare.hpp.
|
inline |
Computes the square eucludian distance of two ranges according to a mask sequence : 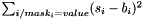 .
.
| first1 | An InputIterator. |
| last1 | An InputIterator. |
| mask_first | An input iterator. |
| first2 | An InputIterator. |
| value | true value of the mask range. Default is 1. |
Definition at line 1101 of file compare.hpp.
|
inline |
Computes the L22 norm ( 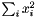 ) of a range.
) of a range.
| first | An InputIterator. |
| last | An InputIterator. |
|
inline |
Computes the L22 norm 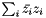 of a complex container.
of a complex container.
| first | An InputIterator. |
| last | An InputIterator. |
Definition at line 3105 of file linear_algebra.hpp.
| Value_T slip::L22_norm_if | ( | InputIterator | first, |
| InputIterator | last, | ||
| Predicate | pred | ||
| ) |
Computes the L22 norm 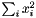 a range according to a Predicate.
a range according to a Predicate.
| first | An input iterator. |
| last | An input iterator. |
| pred | A predicate. |
|
inline |
Computes the L22 norm 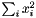 of a range according to a mask sequence.
of a range according to a mask sequence.
| first | An InputIterator. |
| last | An InputIterator. |
| mask_first | An input iterator. |
| value | true value of the mask range. Default is 1. |
|
inline |
Computes the Euclidian distance of two ranges : 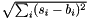 .
.
| first1 | An InputIterator. |
| last1 | An InputIterator. |
| first2 | An InputIterator. |
Definition at line 1197 of file compare.hpp.
| Real slip::L2_distance_if | ( | InputIterator1 | first1, |
| InputIterator1 | last1, | ||
| InputIterator2 | first2, | ||
| Predicate | pred | ||
| ) |
Computes the eucludian distance of two ranges according to a Predicate.
| first1 | An input iterator. |
| last1 | An input iterator. |
| first2 | An input iterator. |
| pred | A predicate. |
Definition at line 1281 of file compare.hpp.
|
inline |
Computes the eucludian distance of two ranges according to a mask sequence : 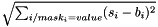 .
.
| first1 | An InputIterator. |
| last1 | An InputIterator. |
| mask_first | An input iterator. |
| first2 | An InputIterator. |
| value | true value of the mask range. Default is 1. |
Definition at line 1234 of file compare.hpp.
|
inline |
Computes the L2 norm 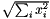 of a range.
of a range.
| first | An InputIterator. |
| last | An InputIterator. |
| Value_T slip::L2_norm_if | ( | InputIterator | first, |
| InputIterator | last, | ||
| Predicate | pred | ||
| ) |
Computes the Euclidean norm 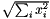 a range according to a Predicate.
a range according to a Predicate.
| first | An input iterator. |
| last | An input iterator. |
| pred | A predicate. |
|
inline |
Computes the Euclidean norm 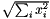 of a range according to a mask sequence.
of a range according to a mask sequence.
| first | An InputIterator. |
| last | An InputIterator. |
| mask_first | An input iterator. |
| value | true value of the mask range. Default is 1. |
|
inline |
Implements the three term recurrence relation for the Laguerre multivariate polynomials, this function can be used to create a sequence of orthogonal polynomial, and for rising k. This recurrence relation holds for Laguere Polynomials:
![\[ P_{k+1}(x) = \frac{(2k+1 - x)P_k(x)-kP_{k-1}(x)}{k+1}\]](../../form_240.png)
.
| k | The degree of the last polynomial calculated. |
| x | The x polynomial. |
| Pk | The value of the polynomial evaluated at degree k. |
| Pkm1 | The value of the polynomial evaluated at degree k-1. |
Definition at line 701 of file polynomial_algo.hpp.
|
inline |
Implements the three term recurrence relation for the Laguerre polynomials, this function can be used to create a sequence of orthogonal polynomial, and for rising k. This recurrence relation holds for Laguerre Polynomials:
![\[ P_{k+1}(x) = \frac{(2k+1 - x)P_k(x)-kP_{k-1}(x)}{k+1}\]](../../form_240.png)
.
| k | The degree of the last polynomial calculated. |
| x | The x polynomial. |
| Pk | The value of the polynomial evaluated at degree k. |
| Pkm1 | The value of the polynomial evaluated at degree k-1. |
Definition at line 649 of file polynomial_algo.hpp.
| void slip::LDLT_decomposition | ( | Container2d & | A | ) |
in place LU decomposition for symmetric matrix
![\[A = LDL^T\]](../../form_119.png)
| A | a unit lower triangular matrix. |
Definition at line 9633 of file linear_algebra.hpp.
| void slip::LDLT_decomposition | ( | const Matrix1 & | A, |
| Matrix2 & | L, | ||
| Vector1 & | D, | ||
| Matrix3 & | LT | ||
| ) |
in place LU decomposition for symmetric matrix
![\[A = LDL^T\]](../../form_119.png)
| A | The matrix to decompose. |
| L | The lower triangular matrix. |
| D | The diagonal matrix. |
| LT | The transposed matrix of L. |
Definition at line 9683 of file linear_algebra.hpp.
| void slip::LDLT_solve | ( | const Matrix1 & | A, |
| Vector1 & | X, | ||
| const Vector2 & | B | ||
| ) |
LDLT solve of system AX = B with A a square symmetric Matrix. 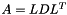 with L a lower triangular matrix.
with L a lower triangular matrix.
| A | 2D container. |
| X | 1D container. |
| B | 1D container. |
!!!!!!!!!!!!!!!!!!!!!!!!!!!!REPLACE 1E-06 by precision
Definition at line 9738 of file linear_algebra.hpp.
|
inline |
Apply left Givens rotation multiplication.
Perform a left multiplication of a matrix M with the transpose Givens matrix on the row1 and row2 between the indices col1 and col2.
| M | the Container to multiply |
| row1 | the first row involved in the computation. |
| row2 | the second row involved in the computation. |
| sinus | Givens sinus. |
| cosinus | Givens cosinus. |
| col1 | the first column index. |
| col2 | the second column index. |
Definition at line 10798 of file linear_algebra.hpp.
|
inline |
Computes Q = Q1Q2...Qn from the inplace Householder QR decomposition.
| M | 2D Container. |
| V0 | The Vector of the initial value of householder vectors |
| Q | The accumulated matrix Q. |
Definition at line 11154 of file linear_algebra.hpp.
|
inline |
Left multiplies the Householder matrix P with the matrix M:
![\[ M = (I - vv^H)M \]](../../form_136.png)
.
| V_first | RandomAccessIterator to the beginning of the sequence (V) |
| V_last | RandomAccessIterator to one-past-the end of the sequence (V) |
| M_up | 2D iterator on the upper_left element of M. |
| M_bot | 2D iterator on the bottom_right_left element of M. |
Definition at line 11111 of file linear_algebra.hpp.
|
inline |
Implements the three term recurrence relation for the Legendre multivariate polynomials, this function can be used to create a sequence of orthogonal polynomial, and for rising k. This recurrence relation holds for Legendre Polynomials of both the first and second kinds:
![\[ \frac{(2k+1)xPk(x)-kP_{k-1}}{k+1}\]](../../form_187.png)
.
| k | The degree of the last polynomial calculated. |
| x | The x polynomial. |
| Pk | The value of the polynomial evaluated at degree k. |
| Pkm1 | The value of the polynomial evaluated at degree k-1. |
Definition at line 133 of file polynomial_algo.hpp.
|
inline |
Implements the three term recurrence relation for the Legendre polynomials, this function can be used to create a sequence of orthogonal polynomial, and for rising k. This recurrence relation holds for Legendre Polynomials of both the first and second kinds:
![\[ \frac{(2k+1)xPk(x)-kP_{k-1}}{k+1}\]](../../form_187.png)
.
| k | The degree of the last polynomial calculated. |
| x | The x polynomial. |
| Pk | The value of the polynomial evaluated at degree k. |
| Pkm1 | The value of the polynomial evaluated at degree k-1. |
Definition at line 172 of file polynomial_algo.hpp.
|
inline |
Computes the Linfinite distance of two ranges : 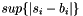 .
.
| first1 | An InputIterator. |
| last1 | An InputIterator. |
| first2 | An InputIterator. |
Definition at line 1636 of file compare.hpp.
| Real slip::Linf_distance_if | ( | InputIterator1 | first1, |
| InputIterator1 | last1, | ||
| InputIterator2 | first2, | ||
| Predicate | pred | ||
| ) |
Computes the Linfinite distance of two ranges according to a Predicate.
| first1 | An input iterator. |
| last1 | An input iterator. |
| first2 | An input iterator. |
| pred | A predicate. |
Definition at line 1735 of file compare.hpp.
|
inline |
Computes the Linfinite distance of two ranges according to a mask sequence : 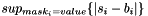 .
.
| first1 | An InputIterator. |
| last1 | An InputIterator. |
| mask_first | An input iterator. |
| first2 | An InputIterator. |
| value | true value of the mask range. Default is 1. |
Definition at line 1679 of file compare.hpp.
| T slip::LM_chi2 | ( | RandomAccessIterator | first, |
| RandomAccessIterator | last | ||
| ) |
Computes Chi2 for Lebvenberg Marquardt algorithm.
| first | RandomAccessIterator to the first element of the data. |
| last | RandomAccessIterator to one-past-the-end element of the data. |
Definition at line 242 of file levenberg_marquardt.hpp.
|
related |
Definition at line 1575 of file KVector.hpp.
|
related |
Definition at line 2143 of file Vector.hpp.
|
related |
Definition at line 2156 of file Signal.hpp.
|
related |
Definition at line 4022 of file Matrix.hpp.
|
related |
Definition at line 5146 of file HyperVolume.hpp.
|
related |
Definition at line 5155 of file Matrix4d.hpp.
|
related |
Definition at line 5796 of file Matrix3d.hpp.
|
related |
Definition at line 6113 of file Volume.hpp.
|
related |
Definition at line 1611 of file KVector.hpp.
|
related |
Definition at line 2179 of file Vector.hpp.
|
related |
Definition at line 2192 of file Signal.hpp.
|
related |
Definition at line 4058 of file Matrix.hpp.
|
related |
Definition at line 5182 of file HyperVolume.hpp.
|
related |
Definition at line 5191 of file Matrix4d.hpp.
|
related |
Definition at line 5832 of file Matrix3d.hpp.
|
related |
Definition at line 6149 of file Volume.hpp.
|
inline |
|
inline |
Solve the linear system L*X=B when L is p lower banded
![\[ \left( \begin{array}{ccccccc} l_{1,1} & 0&\cdots&\cdots&\cdots&\cdots&0\\ l_{2,1} & l_{2,2} & \ddots&&&&\vdots\\ \vdots&&\ddots&\ddots&&&\vdots\\ l_{p+1,1}&&&\ddots&\ddots&&\vdots\\ 0&\ddots&&&\ddots&\ddots&\vdots\\ \vdots&\ddots&\ddots&&&l_{n-1,n-1}&0\\ 0&\cdots&0&l_{n,n-q}&\cdots&l_{n,n-1}&l_{n,n}\\ \end{array}\right) \left( \begin{array}{c} x_{1}\\ x_{2}\\ \vdots\\ x_{n}\\ \end{array}\right) = \left( \begin{array}{c} b_{1}\\ b_{2}\\ \vdots\\ b_{n}\\ \end{array}\right) \]](../../form_100.png)
.
| L_up | 2D iterator corresponding to the upper_left element of the matrix L |
| L_bot | 2D iterator corresponding to one past-the-end bottom_right of the matrix L |
| p | Width of the lower band. |
| X_first | RandomAccessIterator point to the first element of X. |
| X_last | RandomAccessIterator point one-past-the-end element of X. |
| B_first | RandomAccessIterator point to the first element of B. |
| B_last | RandomAccessIterator to one-past-the-end element of B. |
| precision |
Definition at line 7273 of file linear_algebra.hpp.
| void slip::lower_bidiagonal_inv | ( | RandomAccessIterator1 | diag_first, |
| RandomAccessIterator1 | diag_last, | ||
| RandomAccessIterator1 | low_diag_first, | ||
| RandomAccessIterator1 | low_diag_last, | ||
| RandomAccessIterator2d | Ainv_up, | ||
| RandomAccessIterator2d | Ainv_bot, | ||
| typename slip::lin_alg_traits< typename std::iterator_traits< RandomAccessIterator1 >::value_type >::value_type | precision = typename slip::lin_alg_traits<typename std::iterator_traits<RandomAccessIterator1>::value_type>::value_type(1.0E-6) |
||
| ) |
Invert a lower bidiagonal matrix:
![\[ \left( \begin{array}{ccccc} d_{1} & 0&\cdots&\cdots&0\\ l_{1} & d_{2} & \ddots&&\vdots\\ 0&l_{2}&\ddots&\ddots&\vdots\\ \vdots&\ddots&\ddots&\ddots&0\\ 0&\cdots&0&l_{n-1}&d_{n}\\ \end{array}\right)^{-1} \]](../../form_106.png)
.
| diag_first | RandomAccessIterator to the beginning of the main diagonal. |
| diag_last | RandomAccessIterator to one-past-the-end of the main diagonal. |
| low_diag_first | RandomAccessIterator to the beginning of the first lower diagonal. |
| low_diag_last | RandomAccessIterator to one-past-the-end of the first lower diagonal. |
| Ainv_up | RandomAccessIterator2d to the upper_left element of the 2d range of the inverse matrix. |
| Ainv_bot | RandomAccessIterator2d to the one past the bottom_right element of the 2d range of the inverse matrix. |
| precision | 1.0E-6 by default. |
Definition at line 8182 of file linear_algebra.hpp.
| void slip::lower_bidiagonal_inv | ( | const Container2d1 & | A, |
| Container2d2 & | Ainv, | ||
| typename slip::lin_alg_traits< typename Container2d1::value_type >::value_type | precision = typename slip::lin_alg_traits<typename Container2d1::value_type>::value_type(1.0E-6) |
||
| ) |
Invert a lower bidiagonal matrix:
![\[ \left( \begin{array}{ccccc} d_{1} & 0&\cdots&\cdots&0\\ l_{1} & d_{2} & \ddots&&\vdots\\ 0&l_{2}&\ddots&\ddots&\vdots\\ \vdots&\ddots&\ddots&\ddots&0\\ 0&\cdots&0&l_{n-1}&d_{n}\\ \end{array}\right)^{-1} \]](../../form_106.png)
.
| A | 2d container of the matrix to invert. |
| Ainv | 2d container of the matrix the inverse matrix. |
| precision | 1.0E-6 by default. |
Definition at line 8259 of file linear_algebra.hpp.
| void slip::lower_bidiagonal_solve | ( | RandomAccessIterator1 | diag_first, |
| RandomAccessIterator1 | diag_last, | ||
| RandomAccessIterator1 | low_diag_first, | ||
| RandomAccessIterator1 | low_diag_last, | ||
| RandomAccessIterator2 | X_first, | ||
| RandomAccessIterator2 | X_last, | ||
| RandomAccessIterator3 | B_first, | ||
| RandomAccessIterator3 | B_last, | ||
| typename slip::lin_alg_traits< typename std::iterator_traits< RandomAccessIterator1 >::value_type >::value_type | precision = typename slip::lin_alg_traits<typename std::iterator_traits<RandomAccessIterator1>::value_type>::value_type(1.0E-6) |
||
| ) |
solve Ax = B with A lower bidiagonal
![\[ \left( \begin{array}{ccccc} dl_1 & 0&\cdots&\cdots&0\\ ll_1 & dl_2 & \ddots&&\vdots\\ 0&ll_2&\ddots&\ddots&\vdots\\ \vdots&\ddots&\ddots&\ddots&0\\ 0&\cdots&0&ll_{n-1}&dl_{n}\\ \end{array}\right) \left( \begin{array}{c} x_{1}\\ x_{2}\\ \vdots\\ x_n\\ \end{array}\right) = \left( \begin{array}{c} b_{1}\\ b_{2}\\ \vdots\\ b_n\\ \end{array}\right) \]](../../form_105.png)
| diag_first | RandomAccessIterator to the first element of thediagonal. |
| diag_last | RandomAccessIterator to one-past-the-end element of the diagonal. |
| low_diag_first | RandomAccessIterator to the first element of the lower diagonal. |
| low_diag_last | RandomAccessIterator to one-past-the-end element of the lower diagonal. |
| X_first | RandomAccessIterator to the begenning of the result range. |
| X_last | RandomAccessIterator to one-past-the-end of the result range. |
| B_first | RandomAccessIterator to the begenning of the B range. |
| B_last | RandomAccessIterator to one-past-the-end of the B range. |
| precision | 1.0E-6 by default. |
Definition at line 8101 of file linear_algebra.hpp.
|
inline |
Invert a lower triangular Matrix
![\[ \left( \begin{array}{cccc} l_{1,1} & 0&\cdots&0\\ l_{2,1} & l_{2,2} & \ddots&\vdots\\ \vdots&\ddots&\ddots&0\\ l_{n,1}&\cdots&l_{n,n-1}&l_{n,n}\\ \end{array}\right)^{-1} \]](../../form_92.png)
.
| A_up | 2D iterator corresponding to the upper_left element of the matrix A |
| A_bot | 2D iterator corresponding to one past-the-end bottom_right of the matrix A |
| Ainv_up | 2D iterator corresponding to the upper_left element of the inverse matrix. |
| Ainv_bot | 2D iterator corresponding to one past-the-end bottom_right of the inverse matrix. |
| precision | 1.0E-6 by default. |
Definition at line 6212 of file linear_algebra.hpp.
|
inline |
Invert a lower triangular Matrix
![\[ \left( \begin{array}{cccc} l_{1,1} & 0&\cdots&0\\ l_{2,1} & l_{2,2} & \ddots&\vdots\\ \vdots&\ddots&\ddots&0\\ l_{n,1}&\cdots&l_{n,n-1}&l_{n,n}\\ \end{array}\right)^{-1} \]](../../form_92.png)
.
| A | The matrix to invert. |
| Ainv | The inverted matrix. |
| precision | 1.0E-6 by default. |
Definition at line 6285 of file linear_algebra.hpp.
|
inline |
Solve the linear system L*X=B when L is lower triangular
![\[ \left( \begin{array}{cccc} l_{1,1} & 0&\cdots&0\\ l_{2,1} & l_{2,2} & \ddots&\vdots\\ \vdots&\ddots&\ddots&0\\ l_{n,1}&\cdots&l_{n,n-1}&l_{n,n}\\ \end{array}\right) \left( \begin{array}{c} x_{1}\\ x_{2}\\ \vdots\\ x_{n}\\ \end{array}\right) = \left( \begin{array}{c} b_{1}\\ b_{2}\\ \vdots\\ b_{n}\\ \end{array}\right) \]](../../form_91.png)
.
| L_up | 2D iterator corresponding to the upper_left element of the matrix L |
| L_bot | 2D iterator corresponding to one past-the-end bottom_right of the matrix L |
| X_first | RandomAccessIterator point to the first element of X. |
| X_last | RandomAccessIterator point one-past-the-end element of X. |
| B_first | RandomAccessIterator point to the first element of B. |
| B_last | RandomAccessIterator to one-past-the-end element of B. |
| precision |
Definition at line 6048 of file linear_algebra.hpp.
|
inline |
Solve the linear system L*X=B when L is lower triangular
![\[ \left( \begin{array}{cccc} l_{1,1} & 0&\cdots&0\\ l_{2,1} & l_{2,2} & \ddots&\vdots\\ \vdots&\ddots&\ddots&0\\ l_{n,1}&\cdots&l_{n,n-1}&l_{n,n}\\ \end{array}\right) \left( \begin{array}{c} x_{1}\\ x_{2}\\ \vdots\\ x_{n}\\ \end{array}\right) = \left( \begin{array}{c} b_{1}\\ b_{2}\\ \vdots\\ b_{n}\\ \end{array}\right) \]](../../form_91.png)
.
| L | 2D container |
| X | 1D container |
| B | 1D container |
| precision |
Definition at line 6153 of file linear_algebra.hpp.
|
inline |
Computes the LU decomposition according to rows permutations of a matrix using Crout method
![\[ \left( \begin{array}{cccc} m_{1,1} & \cdots&\cdots&m_{1,n}\\ \vdots&&&\vdots\\ \vdots&&&\vdots\\ m_{n,1}&\cdots&\cdots&m_{n,n}\\ \end{array}\right) = \left( \begin{array}{cccc} 1&0&\cdots&0\\ l_{2,1}&\ddots&\ddots&\vdots\\ \vdots&\ddots&\ddots&0\\ l_{n,1}&\cdots&l_{n,n-1}&1\\ \end{array}\right) \left( \begin{array}{cccc} u_{1,1}&\cdots&\cdots&u_{1,n}\\ 0&\ddots&&\vdots\\ \vdots&\ddots&\ddots&\vdots\\ 0&\cdots&0&u_{n,n}\\ \end{array}\right) \]](../../form_86.png)
LU is composed of L and U as following:
![\[ LU = \left( \begin{array}{cccc} u_{1,1}&\cdots&\cdots&u_{1,n}\\ l_{2,1}&\ddots&&\vdots\\ \vdots&\ddots&\ddots&\vdots\\ l_{n,1}&\cdots&l_{n,n-1}&u_{n,n}\\ \end{array}\right) \]](../../form_87.png)
Indx is a vector that records the row permutations effected by the partial pivoting.
| M | Matrix container |
| LU | Matrix container lower and upper matrix in the same container |
| Indx | Vector container for permutation matrix (integer) |
Definition at line 5164 of file linear_algebra.hpp.
|
inline |
Computes the LU decomposition according to rows permutations of a matrix using Crout method
![\[ \left( \begin{array}{cccc} m_{1,1} & \cdots&\cdots&m_{1,n}\\ \vdots&&&\vdots\\ \vdots&&&\vdots\\ m_{n,1}&\cdots&\cdots&m_{n,n}\\ \end{array}\right) = P \left( \begin{array}{cccc} 1&0&\cdots&0\\ l_{2,1}&\ddots&\ddots&\vdots\\ \vdots&\ddots&\ddots&0\\ l_{n,1}&\cdots&l_{n,n-1}&1\\ \end{array}\right) \left( \begin{array}{cccc} u_{1,1}&\cdots&\cdots&u_{1,n}\\ 0&\ddots&&\vdots\\ \vdots&\ddots&\ddots&\vdots\\ 0&\cdots&0&u_{n,n}\\ \end{array}\right) \]](../../form_88.png)
LU is composed of L and U as following:
![\[ LU = \left( \begin{array}{cccc} u_{1,1}&\cdots&\cdots&u_{1,n}\\ l_{2,1}&\ddots&&\vdots\\ \vdots&\ddots&\ddots&\vdots\\ l_{n,1}&\cdots&l_{n,n-1}&u_{n,n}\\ \end{array}\right) \]](../../form_87.png)
P is a permutation matrix needed in case of partial pivoting during the algorithm.
| M | Matrix container |
| L | Matrix container for lower triangular |
| U | Matrix container for upper triangular |
| P | Matrix container for permutation matrix |
Definition at line 5353 of file linear_algebra.hpp.
|
inline |
Computes the determinant of a matrix using LU decomposition.
| M | Matrix container |
Definition at line 5619 of file linear_algebra.hpp.
|
inline |
Computes the inverse of a matrix using LU decomposition.
| M | Matrix container |
| IM | result of the inversion |
Definition at line 5558 of file linear_algebra.hpp.
|
inline |
Solve Linear Equation using LU decomposition.
Solve : A.X=B This function need results from lu method to works
| LU | Matrix container comes from lu method (A in the equation) |
| nr | The number of rows of LU |
| nc | The number of columns of LU |
| Indx | Permutation vector comes from UDecomposition method |
| nv1 | he number of rows of Indx |
| B | Vector to match |
| nv2 | he number of rows of B |
| X | Result Vector |
| nv3 | he number of rows of X |
Definition at line 5421 of file linear_algebra.hpp.
|
inline |
Solve Linear Equation AX = B using LU decomposition.
Definition at line 5495 of file linear_algebra.hpp.
| void slip::marquardt | ( | Function & | fun, |
| DerivativeFunction & | df, | ||
| slip::Vector< Real > & | par, | ||
| slip::Vector< Real > & | r, | ||
| Real & | calchi2, | ||
| const int | maxiter = 10000, |
||
| const Real | eps = static_cast<Real>(1e-6) |
||
| ) |
Optimization of function using the Levenberg-Marquardt algorithm.
| fun | function to optimize. |
| df | Derivative Function. |
| par | Vector of paramameters. |
| r | Residual vector. |
| chi2 | Residual result. |
| maxiter | Max number of iterations. |
| eps | Criteria of convergence. |
Definition at line 330 of file levenberg_marquardt.hpp.
|
inline |
Computes the matrix matrix multiplication of 2 2d ranges.
| M1_up | 2D iterator on the upper_left element of M1 container |
| M1_bot | 2D iterator on the bottom_right element of M1 container |
| M2_up | 2D iterator on the upper_left element of M2 container |
| M2_bot | 2D iterator on the bottom_right element of M2 container |
| R_up | 2D iterator on the upper_left element of R container |
| R_bot | 2D iterator on the bottom_right element of R container |
Definition at line 1621 of file linear_algebra.hpp.
|
inline |
Computes the multiplication of a two Matrix.
| M1 | The first Matrix container. |
| M2 | The second Matrix container. |
| Result | The container which contains the result of the multiplication |
Definition at line 1688 of file linear_algebra.hpp.
|
inline |
Computes the multiplication of a matrix with its transposate A^T 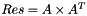 .
.
| M1_up | 2d iterator on the upper_left element of the M1 matrix |
| M1_bot | 2d iterator on the bottom_right element of the M1 matrix |
| Res_up | 2d iterator on the upper_left element of the Res matrix |
| Res_bot | 2d iterator on the bottom_right element of the Res matrix |
Definition at line 2047 of file linear_algebra.hpp.
|
inline |
Computes the multiplication of A and its transposate AT 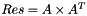 .
.
| M1 | Matrix |
| result | result = AA^T |
Definition at line 2103 of file linear_algebra.hpp.
|
inline |
Computes the multiplication of a Matrix by a scalar R = M*scal.
| M_upper_left | RandomAccessIterator2d to the upper_left matrix element. |
| M_bottom_right | RandomAccessIterator2d to the bottom_right matrix element. |
| R_upper_left | RandomAccessIterator2d to the upper_left matrix element. |
| R_bottom_right | RandomAccessIterator2d to the bottom_right matrix element. |
| scal | Scalar value. |
Definition at line 856 of file linear_algebra.hpp.
|
inline |
Computes the multiplication of a Matrix by a scalar R = M*scal.
| M | Matrix. |
| scal | Scalar value. |
| R | Resulting matrix |
Definition at line 910 of file linear_algebra.hpp.
|
inline |
Computes
![\[ R = A - \lambda I_n\]](../../form_73.png)
with In the identity matrix.
| M_upper_left | RandomAccessIterator2d to the upper_left matrix element. |
| M_bottom_right | RandomAccessIterator2d to the bottom_right matrix element. |
| lambda | Scalar. |
| R_upper_left | RandomAccessIterator2d to the upper_left matrix element. |
| R_bottom_right | RandomAccessIterator2d to the bottom_right matrix element. |
Definition at line 2146 of file linear_algebra.hpp.
|
inline |
Computes
![\[ A = A - \lambda I_n\]](../../form_74.png)
with In the identity matrix.
| M_upper_left | RandomAccessIterator2d to the upper_left matrix element. |
| M_bottom_right | RandomAccessIterator2d to the bottom_right matrix element. |
| lambda | Scalar. |
Definition at line 2206 of file linear_algebra.hpp.
|
inline |
Computes
![\[ R = A - \lambda I_n\]](../../form_73.png)
with In the identity matrix.
| A | The input matrix. |
| lambda | scalar. |
| R | output matrix. |
Definition at line 2259 of file linear_algebra.hpp.
|
inline |
Computes
![\[ A = A - \lambda I_n\]](../../form_74.png)
with In the identity matrix.
| A | The input/output matrix. |
| lambda | scalar. |
Definition at line 2295 of file linear_algebra.hpp.
|
inline |
Computes the multiplication of a Matrix and a Vector: Result=MV.
| M_upper_left | RandomAccessIterator2d to the upper_left matrix element. |
| M_bottom_right | RandomAccessIterator2d to the bottom_right matrix element. |
| first1 | RandomAccessIterator to the first element of the Vector. |
| last1 | RandomAccessIterator to one-past-the-end element of the vector. |
| result_first | RandomAccessIterator to the first element of the result vector. |
| result_last | RandomAccessIterator to one-past-the-end element of the result vector. |
Definition at line 963 of file linear_algebra.hpp.
|
inline |
Computes the multiplication of a Matrix and a Vector: Result=MV.
| M | The Matrix container. |
| V | The Vector container. |
| Result | The container which contains the result of the multiplication |
Definition at line 1030 of file linear_algebra.hpp.
|
inline |
Computes the Householder matrix of a vector V :
![\[ H = I - \frac{2 \times V \times V^{t*}}{V^{t*} \times V} \]](../../form_152.png)
If V is an householder vector of a matrix M then 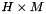 is a matrix with zeros on the first column (except the first element).
is a matrix with zeros on the first column (except the first element).
| H | a 2d container for the householder matrix |
| V_begin | iterator on the first element of V |
| V_end | iterator on the last element of V |
Definition at line 674 of file linear_algebra_qr.hpp.
|
related |
Definition at line 1428 of file KVector.hpp.
|
related |
Definition at line 2006 of file Vector.hpp.
|
related |
Definition at line 2019 of file Signal.hpp.
|
related |
Returns the max element of a GrayscaleImage.
| M1 | the GrayscaleImage |
Definition at line 3704 of file GrayscaleImage.hpp.
|
related |
Definition at line 3885 of file Matrix.hpp.
|
related |
Definition at line 5057 of file HyperVolume.hpp.
|
related |
Definition at line 5066 of file Matrix4d.hpp.
|
related |
Definition at line 5707 of file Matrix3d.hpp.
|
related |
Definition at line 6024 of file Volume.hpp.
|
inline |
Definition at line 1057 of file derivatives.hpp.
|
inline |
Definition at line 1047 of file derivatives.hpp.
| _ForwardIterator slip::max_element_if | ( | _ForwardIterator | first, |
| _ForwardIterator | last, | ||
| Predicate | pred | ||
| ) |
Return the maximum element in a range according to a predicate or last if the predicate is never verified.
| first | An input iterator. |
| last | An input iterator. |
| pred | Predicate. |
Definition at line 483 of file stl_algo_ext.hpp.
| _ForwardIterator slip::max_element_if_compare | ( | _ForwardIterator | first, |
| _ForwardIterator | last, | ||
| Predicate | pred, | ||
| _Compare | comp | ||
| ) |
Return the maximum element in a range using comparison functor according to a predicate or return last if the predicate is never verified.
| first | An input iterator. |
| last | An input iterator. |
| pred | Predicate. |
| comp | Comparison functor. |
Definition at line 603 of file stl_algo_ext.hpp.
| _ForwardIterator slip::max_element_mask | ( | _ForwardIterator | first, |
| _ForwardIterator | last, | ||
| _MaskIterator | mask_first, | ||
| typename std::iterator_traits< _MaskIterator >::value_type | value = typename std::iterator_traits<_MaskIterator>::value_type(1) |
||
| ) |
Return the maximum element in a range according to a mask sequence or return last if no value verify the mask.
| first | An input iterator. |
| last | An input iterator. |
| mask_first | An input iterator. |
| value | true value of the mask range. Default is 1. |
Definition at line 428 of file stl_algo_ext.hpp.
| _ForwardIterator slip::max_element_mask_compare | ( | _ForwardIterator | first, |
| _ForwardIterator | last, | ||
| _MaskIterator | mask_first, | ||
| _Compare | comp, | ||
| typename std::iterator_traits< _MaskIterator >::value_type | value = typename std::iterator_traits<_MaskIterator>::value_type(1) |
||
| ) |
Return the maximum element in a range using comparison functor according to a mask sequence or return last if no value verify the mask.
| first | An input iterator. |
| last | An input iterator. |
| mask_first | An input iterator. |
| comp | Comparison functor. |
| value | true value of the mask range. Default is 1. |
Definition at line 541 of file stl_algo_ext.hpp.
|
inline |
Computes the maximum of two ranges.
| __first1 | An InputIterator. |
| __last1 | An InputIterator. |
| __first2 | An InputIterator. |
| __result | An OutputIterator. |
Definition at line 1081 of file arithmetic_op.hpp.
|
inline |
Computes the maximum of two ranges according to a Predicate.
| __first1 | An input iterator. |
| __last1 | An input iterator. |
| __first2 | An input iterator. |
| __result | An output iterator. |
| __pred | A predicate. |
Definition at line 1222 of file arithmetic_op.hpp.
|
inline |
Computes the maximum of two ranges according to a mask sequence.
| __first1 | An input iterator. |
| __last1 | An input iterator. |
| __mask_first | An input iterator. |
| __first2 | An input iterator. |
| __result | An output iterator. |
| value | true value of the mask range. Default is 1. |
Definition at line 1157 of file arithmetic_op.hpp.
|
inline |
Computes the mean value of a range
![\[ \frac{1}{n}\sum_i x_i\]](../../form_198.png)
.
| first | An InputIterator. |
| last | An InputIterator. |
Definition at line 314 of file statistics.hpp.
|
inline |
Computes the mean absolute difference of two range of size N: 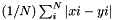 .
.
| first1 | An InputIterator. |
| last1 | An InputIterator. |
| first2 | An InputIterator. |
Definition at line 653 of file compare.hpp.
| Real slip::mean_abs_diff_if | ( | InputIterator1 | first1, |
| InputIterator1 | last1, | ||
| InputIterator2 | first2, | ||
| Predicate | pred | ||
| ) |
Computes the mean absolute difference of two ranges according to a Predicate.
| first1 | An input iterator. |
| last1 | An input iterator. |
| first2 | An input iterator. |
| pred | A predicate. |
Definition at line 756 of file compare.hpp.
|
inline |
Computes the mean absolute difference of two ranges of size N according to a mask sequence : 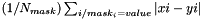 .
.
| first1 | An InputIterator. |
| last1 | An InputIterator. |
| mask_first | An input iterator. |
| first2 | An InputIterator. |
| value | true value of the mask range. Default is 1. |
Definition at line 698 of file compare.hpp.
|
inline |
Computes the mean value of a range using a predicate
![\[ \frac{1}{n}\sum_i x_i\]](../../form_198.png)
.
| first | An InputIterator. |
| last | An InputIterator |
| pred | a predicate function |
Definition at line 2652 of file statistics.hpp.
|
inline |
Computes the mean value of a range over a mask
![\[ \frac{1}{n}\sum_i x_i\]](../../form_198.png)
.
| first | An InputIterator. |
| last | An InputIterator |
| mask_first | An InputIterator on the mask |
| value | Mask value. |
Definition at line 1479 of file statistics.hpp.
| MeanT slip::mean_next | ( | const int | n, |
| const MeanT & | prev_mean, | ||
| const DataT & | xnp1 | ||
| ) |
Recursive mean algorithm.
| n | Current element index. |
| prev_mean | Previous mean value. |
| xnp1 | Next value of the serie. |
Definition at line 4089 of file statistics.hpp.
|
inline |
Computes the mean square of the pointwise difference of two ranges of size N: 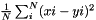 .
.
| first1 | An InputIterator. |
| last1 | An InputIterator. |
| first2 | An InputIterator. |
Definition at line 507 of file compare.hpp.
| Real slip::mean_square_diff_if | ( | InputIterator1 | first1, |
| InputIterator1 | last1, | ||
| InputIterator2 | first2, | ||
| Predicate | pred | ||
| ) |
Computes the mean square of the pointwise difference of two ranges according to a Predicate : 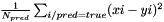 .
.
| first1 | An input iterator. |
| last1 | An input iterator. |
| first2 | An input iterator. |
| pred | A predicate. |
Definition at line 610 of file compare.hpp.
|
inline |
Computes the mean square of the pointwise difference of two ranges of size N according to a mask sequence : 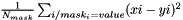 .
.
| first1 | An InputIterator. |
| last1 | An InputIterator. |
| mask_first | An input iterator. |
| first2 | An InputIterator. |
| value | true value of the mask range. Default is 1. |
Definition at line 553 of file compare.hpp.
|
inline |
Computes the median value from a range.
| first | A RandomAccessIterator. |
| last | A RandomAccessIterator. |
Definition at line 1080 of file statistics.hpp.
|
inline |
Computes the median value from a range.
| first | A RandomAccessIterator. |
| last | A RandomAccessIterator. |
| comp | is a model of StrictWeakOrdering. |
Definition at line 1110 of file statistics.hpp.
|
inline |
Computes the median value from a non sorted range.
| first | A RandomAccessIterator. |
| last | A RandomAccessIterator. |
| n | The number of element in the range. |
Definition at line 944 of file statistics.hpp.
|
inline |
Computes the median value from a non sorted range.
| first | A RandomAccessIterator. |
| last | A RandomAccessIterator. |
| n | The number of element in the range. |
| comp | is a model of StrictWeakOrdering. |
Definition at line 979 of file statistics.hpp.
|
inline |
Computes the median value from a sorted range: returns *(first + (last - first) / 2)
| first | A RandomAccessIterator. |
| last | A RandomAccessIterator. |
Definition at line 891 of file statistics.hpp.
|
inline |
Computes the median value from a sorted range using a predicate.
| first | A RandomAccessIterator. |
| last | A RandomAccessIterator. |
| pred | a predicate function |
Definition at line 3334 of file statistics.hpp.
|
inline |
Computes the median value from a sorted range over a mask.
| first | A RandomAccessIterator. |
| last | A RandomAccessIterator. |
| mask_first | An InputIterator on the mask |
| value | Mask value. |
Definition at line 2258 of file statistics.hpp.
|
inline |
Computes the median value from a sorted range: returns *(first + n/2).
| first | A RandomAccessIterator. |
| n | The number of element in the container. |
Definition at line 913 of file statistics.hpp.
|
inline |
Computes the median value from a non sorted range using a predicate.
| first | A RandomAccessIterator. |
| last | A RandomAccessIterator. |
| pred | a predicate function |
Definition at line 3387 of file statistics.hpp.
|
inline |
Computes the median value from a non sorted range over a mask.
| first | A RandomAccessIterator. |
| last | A RandomAccessIterator. |
| mask_first | An InputIterator of the mask |
| value | Mask value. |
Definition at line 2317 of file statistics.hpp.
|
inline |
Computes the median value from a range of size n.
| first | A RandomAccessIterator. |
| last | A RandomAccessIterator. |
| n | Size of the range. |
Definition at line 1140 of file statistics.hpp.
|
inline |
Computes the median value from a range of size n.
| first | A RandomAccessIterator. |
| last | A RandomAccessIterator. |
| n | Size of the range. |
| comp | is a model of StrictWeakOrdering. |
Definition at line 1170 of file statistics.hpp.
|
related |
Definition at line 1421 of file KVector.hpp.
|
related |
Definition at line 1999 of file Vector.hpp.
|
related |
Definition at line 2012 of file Signal.hpp.
|
related |
Returns the min element of a GrayscaleImage.
| M1 | the GrayscaleImage |
Definition at line 3693 of file GrayscaleImage.hpp.
|
related |
Definition at line 3878 of file Matrix.hpp.
|
related |
Definition at line 5050 of file HyperVolume.hpp.
|
related |
Definition at line 5059 of file Matrix4d.hpp.
|
related |
Definition at line 5700 of file Matrix3d.hpp.
|
related |
Definition at line 6017 of file Volume.hpp.
| _ForwardIterator slip::min_element_if | ( | _ForwardIterator | first, |
| _ForwardIterator | last, | ||
| Predicate | pred | ||
| ) |
Return the minimum element in a range according to a predicate or return last if the predicate is never verified.
| first | An input iterator. |
| last | An input iterator. |
| pred | Predicate. |
Definition at line 754 of file stl_algo_ext.hpp.
| _ForwardIterator slip::min_element_if_compare | ( | _ForwardIterator | first, |
| _ForwardIterator | last, | ||
| Predicate | pred, | ||
| _Compare | comp | ||
| ) |
Return the minimum element in a range using comparison functor according to a predicate or return last if the predicate is never verified.
| first | An input iterator. |
| last | An input iterator. |
| pred | Predicate. |
| comp | Comparison functor. |
Definition at line 816 of file stl_algo_ext.hpp.
| _ForwardIterator slip::min_element_mask | ( | _ForwardIterator | first, |
| _ForwardIterator | last, | ||
| _MaskIterator | mask_first, | ||
| typename std::iterator_traits< _MaskIterator >::value_type | value = typename std::iterator_traits<_MaskIterator>::value_type(1) |
||
| ) |
Return the minimum element in a range according to a mask sequence or return last if no value verify the mask.
| first | An input iterator. |
| last | An input iterator. |
| mask_first | An input iterator. |
| value | true value of the mask range. Default is 1. |
Definition at line 658 of file stl_algo_ext.hpp.
| _ForwardIterator slip::min_element_mask_compare | ( | _ForwardIterator | first, |
| _ForwardIterator | last, | ||
| _MaskIterator | mask_first, | ||
| _Compare | comp, | ||
| typename std::iterator_traits< _MaskIterator >::value_type | value = typename std::iterator_traits<_MaskIterator>::value_type(1) |
||
| ) |
Return the minimum element in a range using comparison functor according to a mask sequence or return last if no value verify the mask.
| first | An input iterator. |
| last | An input iterator. |
| mask_first | An input iterator. |
| comp | Comparison functor. |
| value | true value of the mask range. Default is 1. |
Definition at line 717 of file stl_algo_ext.hpp.
|
inline |
Computes the minimum of two ranges.
| __first1 | An InputIterator. |
| __last1 | An InputIterator. |
| __first2 | An InputIterator. |
| __result | An OutputIterator. |
Definition at line 891 of file arithmetic_op.hpp.
|
inline |
Computes the minimum of two ranges according to a Predicate.
| __first1 | An input iterator. |
| __last1 | An input iterator. |
| __first2 | An input iterator. |
| __result | An output iterator. |
| __pred | A predicate. |
Definition at line 1032 of file arithmetic_op.hpp.
|
inline |
Computes the minimum of two ranges according to a mask sequence.
| __first1 | An input iterator. |
| __last1 | An input iterator. |
| __mask_first | An input iterator. |
| __first2 | An input iterator. |
| __result | An output iterator. |
| value | true value of the mask range. Default is 1. |
Definition at line 967 of file arithmetic_op.hpp.
|
inline |
Computes the Minkowski order n distance of two ranges : 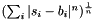 Use L1 and L2 distance for n=1 or 2.
Use L1 and L2 distance for n=1 or 2.
| n | order of the minkowksi distance |
| first1 | An InputIterator. |
| last1 | An InputIterator. |
| first2 | An InputIterator. |
Definition at line 1457 of file compare.hpp.
|
inline |
Computes the Minkowski order n distance of two ranges according to a Predicate.
| n | order of the minkowksi distance |
| first1 | An input iterator. |
| last1 | An input iterator. |
| first2 | An input iterator. |
| pred | A predicate. |
Definition at line 1581 of file compare.hpp.
|
inline |
Computes the Minkowski order n distance of two ranges according to a mask sequence : 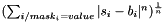 .
.
| n | order of the minkowksi distance |
| first1 | An InputIterator. |
| last1 | An InputIterator. |
| mask_first | An input iterator. |
| first2 | An InputIterator. |
| value | true value of the mask range. Default is 1. |
Definition at line 1512 of file compare.hpp.
|
inline |
Definition at line 1027 of file derivatives.hpp.
|
inline |
Computes the difference of two ranges.
| __first1 | An InputIterator. |
| __last1 | An InputIterator. |
| __first2 | An InputIterator. |
| __result | An OutputIterator. |
Definition at line 315 of file arithmetic_op.hpp.
|
inline |
Computes the difference of two ranges according to a Predicate.
| __first1 | An input iterator. |
| __last1 | An input iterator. |
| __first2 | An input iterator. |
| __result | An output iterator. |
| __pred | A predicate. |
Definition at line 458 of file arithmetic_op.hpp.
|
inline |
Computes the difference of two ranges according to a mask sequence.
| __first1 | An input iterator. |
| __last1 | An input iterator. |
| __mask_first | An input iterator. |
| __first2 | An input iterator. |
| __result | An output iterator. |
| value | true value of the mask range. Default is 1. |
Definition at line 392 of file arithmetic_op.hpp.
|
inline |
Substracts a scalar to a range.
| __first1 | An InputIterator. |
| __last1 | An InputIterator. |
| scalar | A scalar value. |
| __result | An OutputIterator. |
Definition at line 1433 of file arithmetic_op.hpp.
|
inline |
Substracts a scalar to a range according to a Predicate.
| __first1 | An input iterator. |
| __last1 | An input iterator. |
| scalar | A scalar value. |
| __result | An output iterator. |
| __pred | A predicate. |
Definition at line 1556 of file arithmetic_op.hpp.
|
inline |
Substracts a scalar to a range according to a mask sequence.
| __first1 | An input iterator. |
| __last1 | An input iterator. |
| __mask_first | An input iterator. |
| scalar | A scalar value. |
| __result | An output iterator. |
| value | true value of the mask range. Default is 1. |
Definition at line 1499 of file arithmetic_op.hpp.
| void slip::modified_gram_schmidt | ( | MatrixIterator1 | A_up, |
| MatrixIterator1 | A_bot, | ||
| MatrixIterator2 | Q_up, | ||
| MatrixIterator2 | Q_bot, | ||
| MatrixIterator3 | R_up, | ||
| MatrixIterator3 | R_bot | ||
| ) |
Modified Gram-Schmidt orthogonalization algorithm on a matrix.
| A_up | RandomAccessIterator2d to the upper_left of the matrix A. |
| A_bot | RandomAccessIterator2d to the bottom_right of the matrix A. |
| Q_up | RandomAccessIterator2d to the upper_left of the matrix Q. |
| Q_bot | RandomAccessIterator2d to the bottom_right of the matrix Q. |
| R_up | RandomAccessIterator2d to the upper_left of the matrix R. |
| R_bot | RandomAccessIterator2d to the bottom_right of the matrix R. |
Definition at line 390 of file gram_schmidt.hpp.
| void slip::modified_gram_schmidt_normalization | ( | RandomAccessIterator | init_base_first, |
| RandomAccessIterator | init_base_end, | ||
| RandomAccessIterator | ortho_base_first, | ||
| RandomAccessIterator | ortho_base_end, | ||
| InnerProduct | inner_prod | ||
| ) |
Modified Gram-Schmidt orthonormalization algorithm.
| init_base_first | RandomAccessIterator to the first element of the Base to process. |
| init_base_end | RandomAccessIterator to one past the last element of the Base to process. |
| ortho_base_first | RandomAccessIterator to the first element of the resulting Base. |
| ortho_base_end | RandomAccessIterator to one past the last element of the resulting Base. |
| inner_prod | BinaryFunction traducing the InnerProduct to use. |
Definition at line 189 of file gram_schmidt.hpp.
| void slip::modified_gram_schmidt_orthogonalization | ( | RandomAccessIterator | init_base_first, |
| RandomAccessIterator | init_base_end, | ||
| RandomAccessIterator | ortho_base_first, | ||
| RandomAccessIterator | ortho_base_end, | ||
| InnerProduct | inner_prod | ||
| ) |
Modified Gram-Schmidt orthogonalization algorithm.
| init_base_first | RandomAccessIterator to the first element of the Base to process. |
| init_base_end | RandomAccessIterator to one past the last element of the Base to process. |
| ortho_base_first | RandomAccessIterator to the first element of the resulting Base. |
| ortho_base_end | RandomAccessIterator to one past the last element of the resulting Base. |
| inner_prod | BinaryFunction traducing the InnerProduct to use. |
Definition at line 312 of file gram_schmidt.hpp.
| void slip::multi_threshold | ( | InputIterator1 | first, |
| InputIterator1 | last, | ||
| RandomAccessIterator1 | first_th, | ||
| RandomAccessIterator1 | last_th, | ||
| RandomAccessIterator2 | first_level, | ||
| RandomAccessIterator2 | last_level, | ||
| OutputIterator | result_first, | ||
| OutputIterator | result_last | ||
| ) |
multi_threshold algorithm It is equivalent to a quantification J[i] = Level[i] if T[i-1] < I[i] <= T[i]
| first | InputIterator to the input data. |
| last | InputIterator to the input data. |
| first_th | RandomAccessIterator to the threshold data. |
| last_th | RandomAccessIterator to the threshold data. |
| first_level | InputIterator to the level data. |
| last_level | InputIterator to the level data. |
| result_first | OutputIterator to the output data. |
| result_last | OutputIterator to the output data. |
Definition at line 341 of file threshold.hpp.
|
inline |
Computes the pointwise product of two ranges.
| __first1 | An InputIterator. |
| __last1 | An InputIterator. |
| __first2 | An InputIterator. |
| __result | An OutputIterator. |
Definition at line 508 of file arithmetic_op.hpp.
|
inline |
Computes the multiplication of two Matrix.
| M1 | The first Matrix container |
| nr1 | The number of rows of M1 |
| nc1 | The number of columns of M1 |
| M2 | The second Matrix container |
| nr2 | The number of rows of M2 |
| nc2 | The number of columns of M2 |
| Result | The container which contains the result of the multiplication |
| nr3 | The number of rows of Result |
| nc3 | The number of columns of Result |
Definition at line 1846 of file linear_algebra.hpp.
|
inline |
Computes the multiplication of a Matrix with a Vector.
| M | The Matrix container |
| nrm | The number of rows of M |
| ncm | The number of columns of M |
| V | The Vector container |
| nrv | The number of rows of V |
| Result | The container which contains the result of the multiplication |
| nrr | The number of columns of Result |
Definition at line 1896 of file linear_algebra.hpp.
|
inline |
Computes the multiplication of two Matrix.
Definition at line 1950 of file linear_algebra.hpp.
|
inline |
Computes the multiplication of two matrices 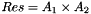 .
.
| A1_up | 2d iterator on the upper_left element of the A1 matrix |
| A1_bot | 2d iterator on the bottom_right element of the A1 matrix |
| A2_up | 2d iterator on the upper_left element of the A2 matrix |
| A2_bot | 2d iterator on the bottom_right element of the A2 matrix |
| Res_up | 2d iterator on the upper_left element of the Res matrix |
| Res_bot | 2d iterator on the bottom_right element of the Res matrix |
Definition at line 1987 of file linear_algebra.hpp.
|
inline |
Computes the pointwise product of two ranges according to a Predicate.
| __first1 | An input iterator. |
| __last1 | An input iterator. |
| __first2 | An input iterator. |
| __result | An output iterator. |
| __pred | A predicate. |
Definition at line 652 of file arithmetic_op.hpp.
|
inline |
Computes the pointwise product of two ranges according to a mask sequence.
| __first1 | An input iterator. |
| __last1 | An input iterator. |
| __mask_first | An input iterator. |
| __first2 | An input iterator. |
| __result | An output iterator. |
| value | true value of the mask range. Default is 1. |
Definition at line 585 of file arithmetic_op.hpp.
|
inline |
Multiplies a range by a scalar.
| __first1 | An InputIterator. |
| __last1 | An InputIterator. |
| scalar | A scalar value. |
| __result | An OutputIterator. |
Definition at line 1597 of file arithmetic_op.hpp.
|
inline |
Multiplies a range by a scalar according to a Predicate.
| __first1 | An input iterator. |
| __last1 | An input iterator. |
| scalar | A scalar value. |
| __result | An output iterator. |
| __pred | A predicate. |
Definition at line 1721 of file arithmetic_op.hpp.
|
inline |
Multiplies a range by a scalar according to a mask sequence.
| __first1 | An input iterator. |
| __last1 | An input iterator. |
| __mask_first | An input iterator. |
| scalar | A scalar value. |
| __result | An output iterator. |
| value | true value of the mask range. Default is 1. |
Definition at line 1663 of file arithmetic_op.hpp.
| void slip::n_max_elements | ( | ForwardIterator | first, |
| ForwardIterator | last, | ||
| std::vector< ForwardIterator > & | max, | ||
| const std::size_t | n = 1 |
||
| ) |
finds the n largest elements in the range [first, last).
| first | InputIterator to the first element of the range. |
| last | InputIterator to one past-the-end element of the range. |
| max | std::vector which contains the first iterators i in [first, last) such that the *i are the greatest one in [first, last). The elements are ordered by decreasing order. |
| n | Number of largest elements to find. Default value is 1. |
Definition at line 1268 of file statistics.hpp.
| void slip::n_min_elements | ( | ForwardIterator | first, |
| ForwardIterator | last, | ||
| std::vector< ForwardIterator > & | min, | ||
| const std::size_t | n = 1 |
||
| ) |
finds the n smallest elements in the range [first, last).
| first | InputIterator to the first element of the range. |
| last | InputIterator to one past-the-end element of the range. |
| min | std::vector which contains the first iterators i in [first, last) such that the *i are the smallest one in [first, last). The elements are ordered by increasing order. |
| n | Number of smallest elements to find. Default value is 1. |
Definition at line 1326 of file statistics.hpp.
|
inline |
Computes the standard normalized crosscorrelation between two sequences: 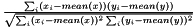 .
.
| first | An InputIterator. |
| last | An InputIterator. |
| first2 | An InputIterator. |
| mean1 | mean value of the first range [first,last). |
| mean2 | mean value of the second range [first2, first2 + (last-first)). |
Definition at line 1378 of file correlation.hpp.
|
inline |
Computes the standard normalized crosscorrelation between two sequences according to a Predicate: 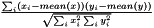 .
.
| first1 | An InputIterator. |
| last1 | An InputIterator. |
| first2 | An InputIterator. |
| pred | A predicate. |
| mean1 | mean value of the first range [first,last). |
| mean2 | mean value of the second range [first2, first2 + (last-first)). |
Definition at line 1473 of file correlation.hpp.
|
inline |
Computes the standard normalized crosscorrelation between two sequences according to a mask sequence 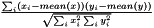 .
.
| first1 | An InputIterator. |
| last1 | An InputIterator. |
| mask_first | An InputIterator. |
| first2 | An InputIterator. |
| mean1 | mean value of the first range [first,last). |
| mean2 | mean value of the second range [first2, first2 + (last-first)). |
| value | true value of the mask range. Default is 1. |
Definition at line 1426 of file correlation.hpp.
|
inline |
Computes the negation of a range.
| __first1 | An InputIterator. |
| __last1 | An InputIterator. |
| __result | An OutputIterator. |
Definition at line 1930 of file arithmetic_op.hpp.
|
inline |
Computes the pointwise negate of a ranges according to a Predicate.
| __first1 | An input iterator. |
| __last1 | An input iterator. |
| __result | An output iterator. |
| __pred | A predicate. |
Definition at line 2043 of file arithmetic_op.hpp.
|
inline |
Computes the negation of a range according to a mask range.
| __first1 | An InputIterator. |
| __last1 | An InputIterator. |
| __mask_first | An InputIterator. |
| __result | An OutputIterator. |
| value | true value of the mask range. Default is 1. |
Definition at line 1992 of file arithmetic_op.hpp.
|
inline |
Computes the standard normalized crosscorrelation between two sequences: 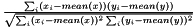 .
.
| first | An InputIterator. |
| last | An InputIterator. |
| first2 | An InputIterator. |
| mean1 | mean value of the first range [first,last). |
| mean2 | mean value of the second range [first2, first2 + (last-first)). |
Definition at line 1179 of file correlation.hpp.
|
inline |
Computes the normalized crosscorrelation between two Images.
| in1_upper_left | : A 2d input iterator (image). |
| in1_bottom_right | : A 2d input iterator (image). |
| in2_upper_left | : A 2d input iterator (mask). |
| in2_bottom_right | : A 2d input iterator (mask). |
| out_upper_left | : A 2d output iterator (result). |
| out_bottom_right | : A 2d output iterator (result). |
Definition at line 2207 of file correlation.hpp.
|
inline |
Computes the standard normalized crosscorrelation between two sequences according to a Predicate: ** 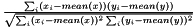 .
.
| first1 | An InputIterator. |
| last1 | An InputIterator. |
| first2 | An InputIterator. |
| pred | A predicate. |
| mean1 | mean value of the first range [first,last). |
| mean2 | mean value of the second range [first2, first2 + (last-first)). |
Definition at line 1305 of file correlation.hpp.
|
inline |
Computes the standard normalized crosscorrelation between two sequences according to a mask sequence 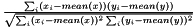 .
.
| first1 | An InputIterator. |
| last1 | An InputIterator. |
| mask_first | An InputIterator. |
| first2 | An InputIterator. |
| mean1 | mean value of the first range [first,last). |
| mean2 | mean value of the second range [first2, first2 + (last-first)). |
| value | true value of the mask range. Default is 1. |
Definition at line 1238 of file correlation.hpp.
|
inline |
Computes the nth moment of a range
![\[\frac{1}{n}\sum_i (x_i-\overline{x})^N\]](../../form_200.png)
.
| first | An InputIterator. |
| last | An InputIterator. |
| mean | The mean of the container itself. |
Definition at line 399 of file statistics.hpp.
|
inline |
Computes the nth moment of a range using a predicate
![\[\frac{1}{n}\sum_i (x_i-\overline{x})^N\]](../../form_200.png)
.
| first | An InputIterator. |
| last | An InputIterator. |
| mean | The mean of the range itself using the predicate. |
| pred | a predicate function |
Definition at line 2707 of file statistics.hpp.
|
inline |
Computes the nth moment of a range over a mask
![\[\frac{1}{n}\sum_i (x_i-\overline{x})^N\]](../../form_200.png)
.
| first | An InputIterator. |
| last | An InputIterator. |
| mask_first | An InputIterator on the mask |
| mean | The mean of the range itself over the mask. |
| value | Mask value. |
Definition at line 1540 of file statistics.hpp.
|
inline |
Computes the nth power of an element 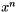 .
.
| x | the element to power |
Definition at line 342 of file macros.hpp.
|
inline |
|
inline |
|
inline |
Definition at line 497 of file Block4d.hpp.
|
inline |
|
inline |
|
inline |
Definition at line 488 of file Block3d.hpp.
|
inline |
| x | A Colormap |
| y | A Colormap of the same type of x |
Definition at line 1016 of file Colormap.hpp.
|
inline |
| x | A kvector |
| y | A kvector of the same type of x |
Definition at line 1630 of file KVector.hpp.
|
inline |
| x | A Matrix3d |
| y | A Matrix3d of the same type of x |
Definition at line 5394 of file Matrix3d.hpp.
|
inline |
| x | A Polynomial |
| y | A Polynomial of the same type of x |
Definition at line 1430 of file Polynomial.hpp.
|
inline |
| x | A Monomial |
| y | A Monomial of the same type of x |
Definition at line 283 of file MultivariatePolynomial.hpp.
|
inline |
| x | A Vector |
| y | A Vector of the same type of x |
Definition at line 2198 of file Vector.hpp.
|
inline |
| x | A Signal |
| y | A Signal of the same type of x |
Definition at line 2211 of file Signal.hpp.
|
inline |
| x | A Array4d |
| y | A Array4d of the same type of x |
Definition at line 4768 of file Array4d.hpp.
|
inline |
| x | A HyperVolume |
| y | A HyperVolume of the same type of x |
Definition at line 4739 of file HyperVolume.hpp.
|
inline |
| x | A Volume |
| y | A Volume of the same type of x |
Definition at line 5713 of file Volume.hpp.
|
inline |
| x | A Array3d |
| y | A Array3d of the same type of x |
Definition at line 5274 of file Array3d.hpp.
|
inline |
| x | A Matrix4d |
| y | A Matrix4d of the same type of x |
Definition at line 4747 of file Matrix4d.hpp.
|
inline |
| x | A GenericMultiComponent3d |
| y | A GenericMultiComponent3d of the same type of x |
Definition at line 7697 of file GenericMultiComponent3d.hpp.
|
inline |
| x | A block2d |
| y | A block2d of the same type of x |
Definition at line 2384 of file Block2d.hpp.
|
inline |
| x | A GenericMultiComponent4d |
| y | A GenericMultiComponent4d of the same type of x |
Definition at line 7357 of file GenericMultiComponent4d.hpp.
|
inline |
| x | A GenericMultiComponent2d |
| y | A GenericMultiComponent2d of the same type of x |
Definition at line 4936 of file GenericMultiComponent2d.hpp.
|
inline |
| x | A Array2d |
| y | A Array2d of the same type of x |
Definition at line 3247 of file Array2d.hpp.
|
inline |
| x | A GrayscaleImage |
| y | A GrayscaleImage of the same type of x |
Definition at line 3722 of file GrayscaleImage.hpp.
|
inline |
| x | A Matrix |
| y | A Matrix of the same type of x |
Definition at line 4077 of file Matrix.hpp.
| bool slip::operator!= | ( | const Pyramid< Container > & | x, |
| const Pyramid< Container > & | y | ||
| ) |
Definition at line 906 of file Pyramid.hpp.
|
inline |
Monomial multiplication.
| monomial1 | A Monomial |
| monomial2 | A Monomial of the same type of monomial1 |
Definition at line 316 of file MultivariatePolynomial.hpp.
|
inline |
pointwise multiplication of two ColorHyperVolume
| M1 | first ColorHyperVolume |
| M2 | second ColorHyperVolume |
Definition at line 777 of file ColorHyperVolume.hpp.
|
inline |
multiplication of a scalar to each element of a ColorHyperVolume
| M1 | the ColorHyperVolume |
| val | the scalar |
Definition at line 790 of file ColorHyperVolume.hpp.
|
inline |
multiplication of a scalar to each element of a ColorHyperVolume
| val | the scalar |
| M1 | the ColorHyperVolume |
Definition at line 799 of file ColorHyperVolume.hpp.
|
inline |
multiplication of a Color block to each element of a ColorHyperVolume
| M1 | the ColorHyperVolume |
| val | the Color block |
Definition at line 806 of file ColorHyperVolume.hpp.
|
inline |
multiplication of a Color block to each element of a ColorHyperVolume
| val | the Color block |
| M1 | the ColorHyperVolume |
Definition at line 815 of file ColorHyperVolume.hpp.
|
inline |
pointwise multiplication of two ColorImage
| M1 | first ColorImage |
| M2 | seconf ColorImage |
Definition at line 991 of file ColorImage.hpp.
|
inline |
multiplication of a scalar to each element of a ColorImage
| M1 | the ColorImage |
| val | the scalar |
Definition at line 1021 of file ColorImage.hpp.
|
inline |
multiplication of a scalar to each element of a ColorImage
| val | the scalar |
| M1 | the ColorImage |
Definition at line 1031 of file ColorImage.hpp.
|
inline |
multiplication of a scalar to each element of a DenseVector3dField2d
| M1 | the DenseVector3dField2d |
| val | the scalar |
Definition at line 1095 of file DenseVector3dField2d.hpp.
|
inline |
Definition at line 636 of file Vector2d.hpp.
|
inline |
multiplication of a scalar to each element of a DenseVector3dField2d
| val | the scalar |
| M1 | the DenseVector3dField2d |
Definition at line 1105 of file DenseVector3dField2d.hpp.
|
inline |
Definition at line 647 of file Vector2d.hpp.
|
inline |
Definition at line 657 of file Vector2d.hpp.
|
inline |
|
inline |
|
inline |
|
inline |
Definition at line 690 of file Vector3d.hpp.
|
inline |
Definition at line 703 of file Vector3d.hpp.
|
inline |
Definition at line 713 of file Vector3d.hpp.
|
inline |
Definition at line 723 of file Vector4d.hpp.
|
inline |
Definition at line 736 of file Vector4d.hpp.
|
inline |
pointwise multiplication of two DenseVector3dField2d
| M1 | first DenseVector3dField2d |
| M2 | seconf DenseVector3dField2d |
Definition at line 1189 of file DenseVector3dField2d.hpp.
|
inline |
Definition at line 746 of file Vector4d.hpp.
|
inline |
multiplication of a Vector3d to each element of a DenseVector3dField2d
| M1 | the DenseVector3dField2d |
| val | the Vector3d |
Definition at line 1202 of file DenseVector3dField2d.hpp.
|
inline |
multiplication of a Vector3d to each element of a DenseVector3dField2d
| val | the Vector3d |
| M1 | the DenseVector3dField2d |
Definition at line 1212 of file DenseVector3dField2d.hpp.
|
inline |
multiplication of a scalar to each element of a DenseVector2dField2d
| M1 | the DenseVector2dField2d |
| val | the scalar |
Definition at line 1265 of file DenseVector2dField2d.hpp.
|
inline |
multiplication of a scalar to each element of a DenseVector2dField2d
| val | the scalar |
| M1 | the DenseVector2dField2d |
Definition at line 1275 of file DenseVector2dField2d.hpp.
|
inline |
multiplication of a scalar to each element of a DenseVector3dField3d
| M1 | the DenseVector3dField3d |
| val | the scalar |
Definition at line 1352 of file DenseVector3dField3d.hpp.
|
inline |
multiplication of a scalar to each element of a DenseVector3dField3d
| val | the scalar |
| M1 | the DenseVector3dField3d |
Definition at line 1362 of file DenseVector3dField3d.hpp.
|
inline |
pointwise multiplication of two DenseVector2dField2d
| M1 | first DenseVector2dField2d |
| M2 | seconf DenseVector2dField2d |
Definition at line 1359 of file DenseVector2dField2d.hpp.
|
inline |
multiplication of a Vector2d to each element of a DenseVector2dField2d
| M1 | the DenseVector2dField2d |
| val | the Vector2d |
Definition at line 1372 of file DenseVector2dField2d.hpp.
|
inline |
multiplication of a Vector2d to each element of a DenseVector2dField2d
| val | the Vector2d |
| M1 | the DenseVector2dField2d |
Definition at line 1382 of file DenseVector2dField2d.hpp.
|
inline |
pointwise multiplication of two DenseVector3dField3d
| M1 | first DenseVector3dField3d |
| M2 | seconf DenseVector3dField3d |
Definition at line 1448 of file DenseVector3dField3d.hpp.
|
inline |
multiplication of a Vector3d to each element of a DenseVector3dField3d
| M1 | the DenseVector3dField3d |
| val | the Vector3d |
Definition at line 1462 of file DenseVector3dField3d.hpp.
|
inline |
multiplication of a Vector3d to each element of a DenseVector3dField3d
| val | the Vector3d |
| M1 | the DenseVector3dField3d |
Definition at line 1472 of file DenseVector3dField3d.hpp.
|
inline |
Definition at line 1003 of file ColorImage.hpp.
|
inline |
Definition at line 1013 of file ColorImage.hpp.
|
inline |
pointwise multiplication of two kvector
| V1 | The first kvector |
| V2 | The second kvector |
Definition at line 1364 of file KVector.hpp.
|
inline |
multiplication of a scalar to each element of a kvector
| V | The kvector |
| val | The scalar |
Definition at line 1374 of file KVector.hpp.
|
inline |
multiplication of a scalar to each element of a kvector
| val | The scalar |
| V | The kvector |
Definition at line 1384 of file KVector.hpp.
|
inline |
pointwise multiplication of two Vector
| V1 | The first Vector |
| V2 | The second Vector |
Definition at line 1947 of file Vector.hpp.
|
inline |
multiplication of a scalar to each element of a Vector
| V | The Vector |
| val | The scalar |
Definition at line 1958 of file Vector.hpp.
|
inline |
pointwise multiplication of two Signal
| V1 | The first Signal |
| V2 | The second Signal |
Definition at line 1960 of file Signal.hpp.
|
inline |
multiplication of a scalar to each element of a Vector
| val | The scalar |
| V | The Vector |
Definition at line 1968 of file Vector.hpp.
|
inline |
multiplication of a scalar to each element of a Signal
| V | The Signal |
| val | The scalar |
Definition at line 1971 of file Signal.hpp.
|
inline |
multiplication of a scalar to each element of a Signal
| val | The scalar |
| V | The Signal |
Definition at line 1981 of file Signal.hpp.
|
related |
Definition at line 1368 of file Polynomial.hpp.
|
related |
Definition at line 1390 of file Polynomial.hpp.
|
inline |
multiplication of a scalar to each element of a RegularVector2dField2d
| M1 | the RegularVector2dField2d |
| val | the scalar |
Definition at line 1983 of file RegularVector2dField2d.hpp.
|
related |
Definition at line 1400 of file Polynomial.hpp.
|
inline |
multiplication of a scalar to each element of a RegularVector2dField2d
| val | the scalar |
| M1 | the RegularVector2dField2d |
Definition at line 1993 of file RegularVector2dField2d.hpp.
|
inline |
pointwise multiplication of two RegularVector2dField2d
| M1 | first RegularVector2dField2d |
| M2 | seconf RegularVector2dField2d |
Definition at line 2074 of file RegularVector2dField2d.hpp.
|
inline |
multiplication of a Vector2d to each element of a RegularVector2dField2d
| M1 | the RegularVector2dField2d |
| val | the Vector2d |
Definition at line 2087 of file RegularVector2dField2d.hpp.
|
inline |
multiplication of a Vector2d to each element of a RegularVector2dField2d
| val | the Vector2d |
| M1 | the RegularVector2dField2d |
Definition at line 2097 of file RegularVector2dField2d.hpp.
|
related |
Definition at line 1778 of file MultivariatePolynomial.hpp.
|
related |
Definition at line 1788 of file MultivariatePolynomial.hpp.
|
related |
Definition at line 1798 of file MultivariatePolynomial.hpp.
|
inline |
multiplication of a scalar to each element of a RegularVector3dField3d
| M1 | the RegularVector3dField3d |
| val | the scalar |
Definition at line 2615 of file RegularVector3dField3d.hpp.
|
inline |
multiplication of a scalar to each element of a RegularVector3dField3d
| val | the scalar |
| M1 | the RegularVector3dField3d |
Definition at line 2625 of file RegularVector3dField3d.hpp.
|
inline |
pointwise multiplication of two RegularVector3dField3d
| M1 | first RegularVector3dField3d |
| M2 | seconf RegularVector3dField3d |
Definition at line 2707 of file RegularVector3dField3d.hpp.
|
inline |
multiplication of a Vector3d to each element of a RegularVector3dField3d
| M1 | the RegularVector3dField3d |
| val | the Vector3d |
Definition at line 2719 of file RegularVector3dField3d.hpp.
|
inline |
multiplication of a Vector3d to each element of a RegularVector3dField3d
| val | the Vector3d |
| M1 | the RegularVector3dField3d |
Definition at line 2729 of file RegularVector3dField3d.hpp.
|
inline |
pointwise multiplication of two GrayscaleImage
| M1 | first GrayscaleImage |
| M2 | seconf GrayscaleImage |
Definition at line 3632 of file GrayscaleImage.hpp.
|
inline |
multiplication of a scalar to each element of a GrayscaleImage
| M1 | the GrayscaleImage |
| val | the scalar |
Definition at line 3644 of file GrayscaleImage.hpp.
|
inline |
multiplication of a scalar to each element of a GrayscaleImage
| val | the scalar |
| M1 | the GrayscaleImage |
Definition at line 3654 of file GrayscaleImage.hpp.
|
inline |
pointwise multiplication of two Matrix
| M1 | first Matrix |
| M2 | seconf Matrix |
Definition at line 3815 of file Matrix.hpp.
|
inline |
multiplication of a scalar to each element of a Matrix
| M1 | the Matrix |
| val | the scalar |
Definition at line 3827 of file Matrix.hpp.
|
inline |
multiplication of a scalar to each element of a Matrix
| val | the scalar |
| M1 | the Matrix |
Definition at line 3838 of file Matrix.hpp.
|
inline |
pointwise multiplication of two HyperVolume
| M1 | first HyperVolume |
| M2 | seconf HyperVolume |
Definition at line 4991 of file HyperVolume.hpp.
|
inline |
pointwise multiplication of two Matrix4d
| M1 | first Matrix4d |
| M2 | seconf Matrix4d |
Definition at line 4999 of file Matrix4d.hpp.
|
inline |
multiplication of a scalar to each element of a HyperVolume
| M1 | the HyperVolume |
| val | the scalar |
Definition at line 5006 of file HyperVolume.hpp.
|
inline |
multiplication of a scalar to each element of a Matrix4d
| M1 | the Matrix4d |
| val | the scalar |
Definition at line 5014 of file Matrix4d.hpp.
|
inline |
multiplication of a scalar to each element of a HyperVolume
| val | the scalar |
| M1 | the HyperVolume |
Definition at line 5016 of file HyperVolume.hpp.
|
inline |
multiplication of a scalar to each element of a Matrix4d
| val | the scalar |
| M1 | the Matrix4d |
Definition at line 5024 of file Matrix4d.hpp.
|
inline |
pointwise multiplication of two Matrix3d
| M1 | first Matrix3d |
| M2 | seconf Matrix3d |
Definition at line 5642 of file Matrix3d.hpp.
|
inline |
multiplication of a scalar to each element of a Matrix3d
| M1 | the Matrix3d |
| val | the scalar |
Definition at line 5656 of file Matrix3d.hpp.
|
inline |
multiplication of a scalar to each element of a Matrix3d
| val | the scalar |
| M1 | the Matrix3d |
Definition at line 5666 of file Matrix3d.hpp.
|
inline |
pointwise multiplication of two Volume
| M1 | first Volume |
| M2 | seconf Volume |
Definition at line 5960 of file Volume.hpp.
|
inline |
multiplication of a scalar to each element of a Volume
| M1 | the Volume |
| val | the scalar |
Definition at line 5974 of file Volume.hpp.
|
inline |
multiplication of a scalar to each element of a Volume
| val | the scalar |
| M1 | the Volume |
Definition at line 5984 of file Volume.hpp.
|
inline |
pointwise addition of two ColorHyperVolume
| M1 | first ColorHyperVolume |
| M2 | second ColorHyperVolume |
Definition at line 694 of file ColorHyperVolume.hpp.
|
inline |
addition of a scalar to each element of a ColorHyperVolume
| M1 | the ColorHyperVolume |
| val | the scalar |
Definition at line 707 of file ColorHyperVolume.hpp.
|
inline |
addition of a scalar to each element of a ColorHyperVolume
| val | the scalar |
| M1 | the ColorHyperVolume |
Definition at line 716 of file ColorHyperVolume.hpp.
|
inline |
addition of a Color block to each element of a ColorHyperVolume
| M1 | the ColorHyperVolume |
| val | the Color block |
Definition at line 723 of file ColorHyperVolume.hpp.
|
inline |
addition of a Color block to each element of a ColorHyperVolume
| val | the Color block |
| M1 | the ColorHyperVolume |
Definition at line 732 of file ColorHyperVolume.hpp.
|
inline |
pointwise addition of two ColorImage
| M1 | first ColorImage |
| M2 | seconf ColorImage |
Definition at line 894 of file ColorImage.hpp.
|
inline |
addition of a scalar to each element of a ColorImage
| M1 | the ColorImage |
| val | the scalar |
Definition at line 924 of file ColorImage.hpp.
|
inline |
addition of a scalar to each element of a ColorImage
| val | the scalar |
| M1 | the ColorImage |
Definition at line 934 of file ColorImage.hpp.
|
inline |
Definition at line 574 of file Vector2d.hpp.
|
inline |
Definition at line 585 of file Vector2d.hpp.
|
inline |
addition of a scalar to each element of a DenseVector3dField2d
| M1 | the DenseVector3dField2d |
| val | the scalar |
Definition at line 1058 of file DenseVector3dField2d.hpp.
|
inline |
Definition at line 595 of file Vector2d.hpp.
|
inline |
addition of a scalar to each element of a DenseVector3dField2d
| val | the scalar |
| M1 | the DenseVector3dField2d |
Definition at line 1068 of file DenseVector3dField2d.hpp.
|
inline |
|
inline |
|
inline |
|
inline |
Definition at line 625 of file Vector3d.hpp.
|
inline |
Definition at line 637 of file Vector3d.hpp.
|
inline |
Definition at line 647 of file Vector3d.hpp.
|
inline |
Definition at line 655 of file Vector4d.hpp.
|
inline |
Definition at line 668 of file Vector4d.hpp.
|
inline |
pointwise addition of two DenseVector3dField2d
| M1 | first DenseVector3dField2d |
| M2 | seconf DenseVector3dField2d |
Definition at line 1124 of file DenseVector3dField2d.hpp.
|
inline |
Definition at line 678 of file Vector4d.hpp.
|
inline |
addition of a Vector3d to each element of a DenseVector3dField2d
| M1 | the DenseVector3dField2d |
| val | the Vector3d |
Definition at line 1137 of file DenseVector3dField2d.hpp.
|
inline |
addition of a Vector3d to each element of a DenseVector3dField2d
| val | the Vector3d |
| M1 | the DenseVector3dField2d |
Definition at line 1147 of file DenseVector3dField2d.hpp.
|
inline |
addition of a scalar to each element of a DenseVector2dField2d
| M1 | the DenseVector2dField2d |
| val | the scalar |
Definition at line 1228 of file DenseVector2dField2d.hpp.
|
inline |
addition of a scalar to each element of a DenseVector2dField2d
| val | the scalar |
| M1 | the DenseVector2dField2d |
Definition at line 1238 of file DenseVector2dField2d.hpp.
|
inline |
addition of a scalar to each element of a DenseVector3dField3d
| M1 | the DenseVector3dField3d |
| val | the scalar |
Definition at line 1315 of file DenseVector3dField3d.hpp.
|
inline |
addition of a scalar to each element of a DenseVector3dField3d
| val | the scalar |
| M1 | the DenseVector3dField3d |
Definition at line 1325 of file DenseVector3dField3d.hpp.
|
inline |
pointwise addition of two DenseVector2dField2d
| M1 | first DenseVector2dField2d |
| M2 | seconf DenseVector2dField2d |
Definition at line 1294 of file DenseVector2dField2d.hpp.
|
inline |
addition of a Vector2d to each element of a DenseVector2dField2d
| M1 | the DenseVector2dField2d |
| val | the Vector2d |
Definition at line 1307 of file DenseVector2dField2d.hpp.
|
inline |
addition of a Vector2d to each element of a DenseVector2dField2d
| val | the Vector2d |
| M1 | the DenseVector2dField2d |
Definition at line 1317 of file DenseVector2dField2d.hpp.
|
inline |
pointwise addition of two DenseVector3dField3d
| M1 | first DenseVector3dField3d |
| M2 | seconf DenseVector3dField3d |
Definition at line 1381 of file DenseVector3dField3d.hpp.
|
inline |
addition of a Vector3d to each element of a DenseVector3dField3d
| M1 | the DenseVector3dField3d |
| val | the Vector3d |
Definition at line 1395 of file DenseVector3dField3d.hpp.
|
inline |
Definition at line 906 of file ColorImage.hpp.
|
inline |
addition of a Vector3d to each element of a DenseVector3dField3d
| val | the Vector3d |
| M1 | the DenseVector3dField3d |
Definition at line 1405 of file DenseVector3dField3d.hpp.
|
inline |
Definition at line 916 of file ColorImage.hpp.
|
inline |
pointwise addition of two kvector
| V1 | The first kvector |
| V2 | The second kvector |
Definition at line 1308 of file KVector.hpp.
|
inline |
addition of a scalar to each element of a kvector
| V | The kvector |
| val | The scalar |
Definition at line 1318 of file KVector.hpp.
|
inline |
addition of a scalar to each element of a kvector
| val | The scalar |
| V | The kvector |
Definition at line 1328 of file KVector.hpp.
|
inline |
pointwise addition of two Vector
| V1 | The first Vector |
| V2 | The second Vector |
Definition at line 1888 of file Vector.hpp.
|
inline |
addition of a scalar to each element of a Vector
| V | The Vector |
| val | The scalar |
Definition at line 1900 of file Vector.hpp.
|
inline |
pointwise addition of two Signal
| V1 | The first Signal |
| V2 | The second Signal |
Definition at line 1901 of file Signal.hpp.
|
inline |
addition of a scalar to each element of a Vector
| val | The scalar |
| V | The Vector |
Definition at line 1910 of file Vector.hpp.
|
inline |
addition of a scalar to each element of a Signal
| V | The Signal |
| val | The scalar |
Definition at line 1913 of file Signal.hpp.
|
inline |
addition of a scalar to each element of a Signal
| val | The scalar |
| V | The Signal |
Definition at line 1923 of file Signal.hpp.
|
related |
Definition at line 1312 of file Polynomial.hpp.
|
related |
Definition at line 1322 of file Polynomial.hpp.
|
related |
Definition at line 1332 of file Polynomial.hpp.
|
inline |
addition of a scalar to each element of a RegularVector2dField2d
| M1 | the RegularVector2dField2d |
| val | the scalar |
Definition at line 1946 of file RegularVector2dField2d.hpp.
|
inline |
addition of a scalar to each element of a RegularVector2dField2d
| val | the scalar |
| M1 | the RegularVector2dField2d |
Definition at line 1956 of file RegularVector2dField2d.hpp.
|
inline |
pointwise addition of two RegularVector2dField2d
| M1 | first RegularVector2dField2d |
| M2 | seconf RegularVector2dField2d |
Definition at line 2012 of file RegularVector2dField2d.hpp.
|
inline |
addition of a Vector2d to each element of a RegularVector2dField2d
| M1 | the RegularVector2dField2d |
| val | the Vector2d |
Definition at line 2024 of file RegularVector2dField2d.hpp.
|
inline |
addition of a Vector2d to each element of a RegularVector2dField2d
| val | the Vector2d |
| M1 | the RegularVector2dField2d |
Definition at line 2034 of file RegularVector2dField2d.hpp.
|
related |
Definition at line 1720 of file MultivariatePolynomial.hpp.
|
related |
Definition at line 1730 of file MultivariatePolynomial.hpp.
|
related |
Definition at line 1740 of file MultivariatePolynomial.hpp.
|
inline |
addition of a scalar to each element of a RegularVector3dField3d
| M1 | the RegularVector3dField3d |
| val | the scalar |
Definition at line 2578 of file RegularVector3dField3d.hpp.
|
inline |
addition of a scalar to each element of a RegularVector3dField3d
| val | the scalar |
| M1 | the RegularVector3dField3d |
Definition at line 2588 of file RegularVector3dField3d.hpp.
|
inline |
pointwise addition of two RegularVector3dField3d
| M1 | first RegularVector3dField3d |
| M2 | seconf RegularVector3dField3d |
Definition at line 2644 of file RegularVector3dField3d.hpp.
|
inline |
addition of a Vector3d to each element of a RegularVector3dField3d
| M1 | the RegularVector3dField3d |
| val | the Vector3d |
Definition at line 2656 of file RegularVector3dField3d.hpp.
|
inline |
addition of a Vector3d to each element of a RegularVector3dField3d
| val | the Vector3d |
| M1 | the RegularVector3dField3d |
Definition at line 2666 of file RegularVector3dField3d.hpp.
|
inline |
pointwise addition of two GrayscaleImage
| M1 | first GrayscaleImage |
| M2 | seconf GrayscaleImage |
Definition at line 3571 of file GrayscaleImage.hpp.
|
inline |
addition of a scalar to each element of a GrayscaleImage
| M1 | the GrayscaleImage |
| val | the scalar |
Definition at line 3583 of file GrayscaleImage.hpp.
|
inline |
addition of a scalar to each element of a GrayscaleImage
| val | the scalar |
| M1 | the GrayscaleImage |
Definition at line 3593 of file GrayscaleImage.hpp.
|
inline |
pointwise addition of two Matrix
| M1 | first Matrix |
| M2 | seconf Matrix |
Definition at line 3754 of file Matrix.hpp.
|
inline |
addition of a scalar to each element of a Matrix
| M1 | the Matrix |
| val | the scalar |
Definition at line 3766 of file Matrix.hpp.
|
inline |
addition of a scalar to each element of a Matrix
| val | the scalar |
| M1 | the Matrix |
Definition at line 3776 of file Matrix.hpp.
|
inline |
pointwise addition of two HyperVolume
| M1 | first HyperVolume |
| M2 | seconf HyperVolume |
Definition at line 4924 of file HyperVolume.hpp.
|
inline |
pointwise addition of two Matrix4d
| M1 | first Matrix4d |
| M2 | seconf Matrix4d |
Definition at line 4932 of file Matrix4d.hpp.
|
inline |
addition of a scalar to each element of a HyperVolume
| M1 | the HyperVolume |
| val | the scalar |
Definition at line 4939 of file HyperVolume.hpp.
|
inline |
addition of a scalar to each element of a Matrix4d
| M1 | the Matrix4d |
| val | the scalar |
Definition at line 4947 of file Matrix4d.hpp.
|
inline |
addition of a scalar to each element of a HyperVolume
| val | the scalar |
| M1 | the HyperVolume |
Definition at line 4949 of file HyperVolume.hpp.
|
inline |
addition of a scalar to each element of a Matrix4d
| val | the scalar |
| M1 | the Matrix4d |
Definition at line 4957 of file Matrix4d.hpp.
|
inline |
pointwise addition of two Matrix3d
| M1 | first Matrix3d |
| M2 | seconf Matrix3d |
Definition at line 5577 of file Matrix3d.hpp.
|
inline |
addition of a scalar to each element of a Matrix3d
| M1 | the Matrix3d |
| val | the scalar |
Definition at line 5591 of file Matrix3d.hpp.
|
inline |
addition of a scalar to each element of a Matrix3d
| val | the scalar |
| M1 | the Matrix3d |
Definition at line 5601 of file Matrix3d.hpp.
|
inline |
pointwise addition of two Volume
| M1 | first Volume |
| M2 | seconf Volume |
Definition at line 5895 of file Volume.hpp.
|
inline |
addition of a scalar to each element of a Volume
| M1 | the Volume |
| val | the scalar |
Definition at line 5909 of file Volume.hpp.
|
inline |
addition of a scalar to each element of a Volume
| val | the scalar |
| M1 | the Volume |
Definition at line 5919 of file Volume.hpp.
|
inline |
pointwise subtraction of two ColorHyperVolume
| M1 | first ColorHyperVolume |
| M2 | second ColorHyperVolume |
Definition at line 739 of file ColorHyperVolume.hpp.
|
inline |
subtraction of a scalar to each element of a ColorHyperVolume
| M1 | the ColorHyperVolume |
| val | the scalar |
Definition at line 752 of file ColorHyperVolume.hpp.
|
inline |
subtraction of a scalar to each element of a ColorHyperVolume
| val | the scalar |
| M1 | the ColorHyperVolume |
Definition at line 761 of file ColorHyperVolume.hpp.
|
inline |
subtraction of a Color block to each element of a ColorHyperVolume
| M1 | the ColorHyperVolume |
| val | the Color block |
Definition at line 768 of file ColorHyperVolume.hpp.
|
inline |
pointwise substraction of two ColorImage
| M1 | first ColorImage |
| M2 | seconf ColorImage |
Definition at line 942 of file ColorImage.hpp.
|
inline |
substraction of a scalar to each element of a ColorImage
| M1 | the ColorImage |
| val | the scalar |
Definition at line 972 of file ColorImage.hpp.
|
inline |
substraction of a scalar to each element of a ColorImage
| val | the scalar |
| M1 | the ColorImage |
Definition at line 982 of file ColorImage.hpp.
|
inline |
Definition at line 603 of file Vector2d.hpp.
|
inline |
substraction of a scalar to each element of a DenseVector3dField2d
| M1 | the DenseVector3dField2d |
| val | the scalar |
Definition at line 1076 of file DenseVector3dField2d.hpp.
|
inline |
Definition at line 614 of file Vector2d.hpp.
|
inline |
substraction of a scalar to each element of a DenseVector3dField2d
| val | the scalar |
| M1 | the DenseVector3dField2d |
Definition at line 1086 of file DenseVector3dField2d.hpp.
|
inline |
Definition at line 624 of file Vector2d.hpp.
|
inline |
|
inline |
|
inline |
|
inline |
Definition at line 655 of file Vector3d.hpp.
|
inline |
Definition at line 667 of file Vector3d.hpp.
|
inline |
Definition at line 677 of file Vector3d.hpp.
|
inline |
Definition at line 686 of file Vector4d.hpp.
|
inline |
Definition at line 699 of file Vector4d.hpp.
|
inline |
pointwise substraction of two DenseVector3dField2d
| M1 | first DenseVector3dField2d |
| M2 | seconf DenseVector3dField2d |
Definition at line 1157 of file DenseVector3dField2d.hpp.
|
inline |
Definition at line 709 of file Vector4d.hpp.
|
inline |
substraction of a Vector3d to each element of a DenseVector3dField2d
| M1 | the DenseVector3dField2d |
| val | the Vector3d |
Definition at line 1170 of file DenseVector3dField2d.hpp.
|
inline |
substraction of a Vector3d to each element of a DenseVector3dField2d
| val | the Vector3d |
| M1 | the DenseVector3dField2d |
Definition at line 1180 of file DenseVector3dField2d.hpp.
|
inline |
substraction of a scalar to each element of a DenseVector2dField2d
| M1 | the DenseVector2dField2d |
| val | the scalar |
Definition at line 1246 of file DenseVector2dField2d.hpp.
|
inline |
substraction of a scalar to each element of a DenseVector2dField2d
| val | the scalar |
| M1 | the DenseVector2dField2d |
Definition at line 1256 of file DenseVector2dField2d.hpp.
|
inline |
substraction of a scalar to each element of a DenseVector3dField3d
| M1 | the DenseVector3dField3d |
| val | the scalar |
Definition at line 1333 of file DenseVector3dField3d.hpp.
|
inline |
substraction of a scalar to each element of a DenseVector3dField3d
| val | the scalar |
| M1 | the DenseVector3dField3d |
Definition at line 1343 of file DenseVector3dField3d.hpp.
|
inline |
pointwise substraction of two DenseVector2dField2d
| M1 | first DenseVector2dField2d |
| M2 | seconf DenseVector2dField2d |
Definition at line 1327 of file DenseVector2dField2d.hpp.
|
inline |
substraction of a Vector2d to each element of a DenseVector2dField2d
| M1 | the DenseVector2dField2d |
| val | the Vector2d |
Definition at line 1340 of file DenseVector2dField2d.hpp.
|
inline |
substraction of a Vector2d to each element of a DenseVector2dField2d
| val | the Vector2d |
| M1 | the DenseVector2dField2d |
Definition at line 1350 of file DenseVector2dField2d.hpp.
|
inline |
pointwise substraction of two DenseVector3dField3d
| M1 | first DenseVector3dField3d |
| M2 | seconf DenseVector3dField3d |
Definition at line 1415 of file DenseVector3dField3d.hpp.
|
inline |
substraction of a Vector3d to each element of a DenseVector3dField3d
| M1 | the DenseVector3dField3d |
| val | the Vector3d |
Definition at line 1429 of file DenseVector3dField3d.hpp.
|
inline |
substraction of a Vector3d to each element of a DenseVector3dField3d
| val | the Vector3d |
| M1 | the DenseVector3dField3d |
Definition at line 1439 of file DenseVector3dField3d.hpp.
|
inline |
Definition at line 954 of file ColorImage.hpp.
|
inline |
Definition at line 964 of file ColorImage.hpp.
|
inline |
pointwise substraction of two kvector
| V1 | The first kvector |
| V2 | The second kvector |
Definition at line 1336 of file KVector.hpp.
|
inline |
substraction of a scalar to each element of a kvector
| V | The kvector |
| val | The scalar |
Definition at line 1346 of file KVector.hpp.
|
inline |
substraction of a scalar to each element of a kvector
| val | The scalar |
| V | The kvector |
Definition at line 1356 of file KVector.hpp.
|
inline |
pointwise substraction of two Vector
| V1 | The first Vector |
| V2 | The second Vector |
Definition at line 1918 of file Vector.hpp.
|
inline |
substraction of a scalar to each element of a Vector
| V | The Vector |
| val | The scalar |
Definition at line 1929 of file Vector.hpp.
|
inline |
pointwise substraction of two Signal
| V1 | The first Signal |
| V2 | The second Signal |
Definition at line 1931 of file Signal.hpp.
|
inline |
substraction of a scalar to each element of a Vector
| val | The scalar |
| V | The Vector |
Definition at line 1939 of file Vector.hpp.
|
inline |
substraction of a scalar to each element of a Signal
| V | The Signal |
| val | The scalar |
Definition at line 1942 of file Signal.hpp.
|
inline |
substraction of a scalar to each element of a Signal
| val | The scalar |
| V | The Signal |
Definition at line 1952 of file Signal.hpp.
|
related |
Definition at line 1340 of file Polynomial.hpp.
|
related |
Definition at line 1350 of file Polynomial.hpp.
|
related |
Definition at line 1360 of file Polynomial.hpp.
|
inline |
substraction of a scalar to each element of a RegularVector2dField2d
| M1 | the RegularVector2dField2d |
| val | the scalar |
Definition at line 1964 of file RegularVector2dField2d.hpp.
|
inline |
substraction of a scalar to each element of a RegularVector2dField2d
| val | the scalar |
| M1 | the RegularVector2dField2d |
Definition at line 1974 of file RegularVector2dField2d.hpp.
|
inline |
pointwise substraction of two RegularVector2dField2d
| M1 | first RegularVector2dField2d |
| M2 | seconf RegularVector2dField2d |
Definition at line 2044 of file RegularVector2dField2d.hpp.
|
inline |
substraction of a Vector2d to each element of a RegularVector2dField2d
| M1 | the RegularVector2dField2d |
| val | the Vector2d |
Definition at line 2055 of file RegularVector2dField2d.hpp.
|
inline |
substraction of a Vector2d to each element of a RegularVector2dField2d
| val | the Vector2d |
| M1 | the RegularVector2dField2d |
Definition at line 2065 of file RegularVector2dField2d.hpp.
|
related |
Definition at line 1749 of file MultivariatePolynomial.hpp.
|
related |
Definition at line 1759 of file MultivariatePolynomial.hpp.
|
related |
Definition at line 1769 of file MultivariatePolynomial.hpp.
|
inline |
substraction of a scalar to each element of a RegularVector3dField3d
| M1 | the RegularVector3dField3d |
| val | the scalar |
Definition at line 2596 of file RegularVector3dField3d.hpp.
|
inline |
substraction of a scalar to each element of a RegularVector3dField3d
| val | the scalar |
| M1 | the RegularVector3dField3d |
Definition at line 2606 of file RegularVector3dField3d.hpp.
|
inline |
pointwise substraction of two RegularVector3dField3d
| M1 | first RegularVector3dField3d |
| M2 | seconf RegularVector3dField3d |
Definition at line 2676 of file RegularVector3dField3d.hpp.
|
inline |
substraction of a Vector3d to each element of a RegularVector3dField3d
| M1 | the RegularVector3dField3d |
| val | the Vector3d |
Definition at line 2688 of file RegularVector3dField3d.hpp.
|
inline |
substraction of a Vector3d to each element of a RegularVector3dField3d
| val | the Vector3d |
| M1 | the RegularVector3dField3d |
Definition at line 2698 of file RegularVector3dField3d.hpp.
|
inline |
pointwise substraction of two GrayscaleImage
| M1 | first GrayscaleImage |
| M2 | seconf GrayscaleImage |
Definition at line 3602 of file GrayscaleImage.hpp.
|
inline |
substraction of a scalar to each element of a GrayscaleImage
| M1 | the GrayscaleImage |
| val | the scalar |
Definition at line 3614 of file GrayscaleImage.hpp.
|
inline |
substraction of a scalar to each element of a GrayscaleImage
| val | the scalar |
| M1 | the GrayscaleImage |
Definition at line 3624 of file GrayscaleImage.hpp.
|
inline |
pointwise substraction of two Matrix
| M1 | first Matrix |
| M2 | seconf Matrix |
Definition at line 3785 of file Matrix.hpp.
|
inline |
substraction of a scalar to each element of a Matrix
| M1 | the Matrix |
| val | the scalar |
Definition at line 3797 of file Matrix.hpp.
|
inline |
substraction of a scalar to each element of a Matrix
| val | the scalar |
| M1 | the Matrix |
Definition at line 3807 of file Matrix.hpp.
|
inline |
pointwise substraction of two HyperVolume
| M1 | first HyperVolume |
| M2 | seconf HyperVolume |
Definition at line 4958 of file HyperVolume.hpp.
|
inline |
pointwise substraction of two Matrix4d
| M1 | first Matrix4d |
| M2 | seconf Matrix4d |
Definition at line 4966 of file Matrix4d.hpp.
|
inline |
substraction of a scalar to each element of a HyperVolume
| M1 | the HyperVolume |
| val | the scalar |
Definition at line 4973 of file HyperVolume.hpp.
|
inline |
substraction of a scalar to each element of a Matrix4d
| M1 | the Matrix4d |
| val | the scalar |
Definition at line 4981 of file Matrix4d.hpp.
|
inline |
substraction of a scalar to each element of a HyperVolume
| val | the scalar |
| M1 | the HyperVolume |
Definition at line 4983 of file HyperVolume.hpp.
|
inline |
substraction of a scalar to each element of a Matrix4d
| val | the scalar |
| M1 | the Matrix4d |
Definition at line 4991 of file Matrix4d.hpp.
|
inline |
pointwise substraction of two Matrix3d
| M1 | first Matrix3d |
| M2 | seconf Matrix3d |
Definition at line 5610 of file Matrix3d.hpp.
|
inline |
substraction of a scalar to each element of a Matrix3d
| M1 | the Matrix3d |
| val | the scalar |
Definition at line 5624 of file Matrix3d.hpp.
|
inline |
substraction of a scalar to each element of a Matrix3d
| val | the scalar |
| M1 | the Matrix3d |
Definition at line 5634 of file Matrix3d.hpp.
|
inline |
pointwise substraction of two Volume
| M1 | first Volume |
| M2 | seconf Volume |
Definition at line 5928 of file Volume.hpp.
|
inline |
substraction of a scalar to each element of a Volume
| M1 | the Volume |
| val | the scalar |
Definition at line 5942 of file Volume.hpp.
|
inline |
substraction of a scalar to each element of a Volume
| val | the scalar |
| M1 | the Volume |
Definition at line 5952 of file Volume.hpp.
|
inline |
pointwise division of two ColorHyperVolume
| M1 | first ColorHyperVolume |
| M2 | seconf ColorHyperVolume |
Definition at line 822 of file ColorHyperVolume.hpp.
|
inline |
division of a scalar to each element of a ColorHyperVolume
| M1 | the ColorHyperVolume |
| val | the scalar |
Definition at line 835 of file ColorHyperVolume.hpp.
|
inline |
division of each element of a ColorHyperVolume by a Color block
| M1 | the ColorHyperVolume |
| val | the Color block |
Definition at line 844 of file ColorHyperVolume.hpp.
|
inline |
pointwise division of two ColorImage
| M1 | first ColorImage |
| M2 | seconf ColorImage |
Definition at line 1039 of file ColorImage.hpp.
|
inline |
division of a scalar to each element of a ColorImage
| M1 | the ColorImage |
| val | the scalar |
Definition at line 1061 of file ColorImage.hpp.
|
inline |
division of a scalar to each element of a DenseVector3dField2d
| M1 | the DenseVector3dField2d |
| val | the scalar |
Definition at line 1114 of file DenseVector3dField2d.hpp.
|
inline |
Definition at line 665 of file Vector2d.hpp.
|
inline |
Definition at line 676 of file Vector2d.hpp.
|
inline |
|
inline |
|
inline |
Definition at line 721 of file Vector3d.hpp.
|
inline |
Definition at line 733 of file Vector3d.hpp.
|
inline |
Definition at line 754 of file Vector4d.hpp.
|
inline |
Definition at line 767 of file Vector4d.hpp.
|
inline |
pointwise division of two DenseVector3dField2d
| M1 | first DenseVector3dField2d |
| M2 | seconf DenseVector3dField2d |
Definition at line 1221 of file DenseVector3dField2d.hpp.
|
inline |
division of a Vector3d to each element of a DenseVector3dField2d
| M1 | the DenseVector3dField2d |
| val | the Vector3d |
Definition at line 1234 of file DenseVector3dField2d.hpp.
|
inline |
division of a scalar to each element of a DenseVector2dField2d
| M1 | the DenseVector2dField2d |
| val | the scalar |
Definition at line 1284 of file DenseVector2dField2d.hpp.
|
inline |
division of a scalar to each element of a DenseVector3dField3d
| M1 | the DenseVector3dField3d |
| val | the scalar |
Definition at line 1371 of file DenseVector3dField3d.hpp.
|
inline |
pointwise division of two DenseVector2dField2d
| M1 | first DenseVector2dField2d |
| M2 | seconf DenseVector2dField2d |
Definition at line 1391 of file DenseVector2dField2d.hpp.
|
inline |
division of a Vector2d to each element of a DenseVector2dField2d
| M1 | the DenseVector2dField2d |
| val | the Vector2d |
Definition at line 1404 of file DenseVector2dField2d.hpp.
|
inline |
pointwise division of two DenseVector3dField3d
| M1 | first DenseVector3dField3d |
| M2 | seconf DenseVector3dField3d |
Definition at line 1481 of file DenseVector3dField3d.hpp.
|
inline |
division of a Vector3d to each element of a DenseVector3dField3d
| M1 | the DenseVector3dField3d |
| val | the Vector3d |
Definition at line 1495 of file DenseVector3dField3d.hpp.
|
inline |
Definition at line 1051 of file ColorImage.hpp.
|
inline |
pointwise division of two kvector
| V1 | The first kvector |
| V2 | The second kvector |
Definition at line 1392 of file KVector.hpp.
|
inline |
division of a scalar to each element of a kvector
| V | The kvector |
| val | The scalar |
Definition at line 1402 of file KVector.hpp.
|
inline |
pointwise division of two Vector
| V1 | The first Vector |
| V2 | The second Vector |
Definition at line 1976 of file Vector.hpp.
|
inline |
division of a scalar to each element of a Vector
| V | The Vector |
| val | The scalar |
Definition at line 1987 of file Vector.hpp.
|
inline |
pointwise division of two Signal
| V1 | The first Signal |
| V2 | The second Signal |
Definition at line 1989 of file Signal.hpp.
|
inline |
division of a scalar to each element of a Signal
| V | The Signal |
| val | The scalar |
Definition at line 2000 of file Signal.hpp.
|
related |
Definition at line 1410 of file Polynomial.hpp.
|
inline |
division of a scalar to each element of a RegularVector2dField2d
| M1 | the RegularVector2dField2d |
| val | the scalar |
Definition at line 2002 of file RegularVector2dField2d.hpp.
|
inline |
pointwise division of two RegularVector2dField2d
| M1 | first RegularVector2dField2d |
| M2 | seconf RegularVector2dField2d |
Definition at line 2106 of file RegularVector2dField2d.hpp.
|
inline |
division of a Vector2d to each element of a RegularVector2dField2d
| M1 | the RegularVector2dField2d |
| val | the Vector2d |
Definition at line 2119 of file RegularVector2dField2d.hpp.
|
related |
Definition at line 1807 of file MultivariatePolynomial.hpp.
|
inline |
division of a scalar to each element of a RegularVector3dField3d
| M1 | the RegularVector3dField3d |
| val | the scalar |
Definition at line 2634 of file RegularVector3dField3d.hpp.
|
inline |
pointwise division of two RegularVector3dField3d
| M1 | first RegularVector3dField3d |
| M2 | seconf RegularVector3dField3d |
Definition at line 2738 of file RegularVector3dField3d.hpp.
|
inline |
division of a Vector3d to each element of a RegularVector3dField3d
| M1 | the RegularVector3dField3d |
| val | the Vector3d |
Definition at line 2750 of file RegularVector3dField3d.hpp.
|
inline |
pointwise division of two GrayscaleImage
| M1 | first GrayscaleImage |
| M2 | seconf GrayscaleImage |
Definition at line 3662 of file GrayscaleImage.hpp.
|
inline |
division of a scalar to each element of a GrayscaleImage
| M1 | the GrayscaleImage |
| val | the scalar |
Definition at line 3674 of file GrayscaleImage.hpp.
|
inline |
pointwise division of two Matrix
| M1 | first Matrix |
| M2 | seconf Matrix |
Definition at line 3846 of file Matrix.hpp.
|
inline |
division of a scalar to each element of a Matrix
| M1 | the Matrix |
| val | the scalar |
Definition at line 3858 of file Matrix.hpp.
|
inline |
pointwise division of two HyperVolume
| M1 | first HyperVolume |
| M2 | seconf HyperVolume |
Definition at line 5024 of file HyperVolume.hpp.
|
inline |
pointwise division of two Matrix4d
| M1 | first Matrix4d |
| M2 | seconf Matrix4d |
Definition at line 5032 of file Matrix4d.hpp.
|
inline |
division of a scalar to each element of a HyperVolume
| M1 | the HyperVolume |
| val | the scalar |
Definition at line 5039 of file HyperVolume.hpp.
|
inline |
division of a scalar to each element of a Matrix4d
| M1 | the Matrix4d |
| val | the scalar |
Definition at line 5047 of file Matrix4d.hpp.
|
inline |
pointwise division of two Matrix3d
| M1 | first Matrix3d |
| M2 | seconf Matrix3d |
Definition at line 5674 of file Matrix3d.hpp.
|
inline |
division of a scalar to each element of a Matrix3d
| M1 | the Matrix3d |
| val | the scalar |
Definition at line 5688 of file Matrix3d.hpp.
|
inline |
pointwise division of two Volume
| M1 | first Volume |
| M2 | seconf Volume |
Definition at line 5992 of file Volume.hpp.
|
inline |
division of a scalar to each element of a Volume
| M1 | the Volume |
| val | the scalar |
Definition at line 6006 of file Volume.hpp.
|
inline |
| x | first Vector3d to compare |
| y | second Vector3d to compare return true if ||x|| < ||y||, ||.|| is the Euclidean norm |
Definition at line 480 of file Vector3d.hpp.
|
inline |
| x | first Vector4d to compare |
| y | second Vector4d to compare return true if ||x|| < ||y||, ||.|| is the Euclidean norm |
Definition at line 499 of file Vector4d.hpp.
|
inline |
| x | first Vector2d to compare |
| y | second Vector2d to compare return true if ||x|| < ||y||, ||.|| is the Euclidean norm |
Definition at line 472 of file Vector2d.hpp.
|
inline |
Definition at line 512 of file Block4d.hpp.
|
inline |
Definition at line 503 of file Block3d.hpp.
|
inline |
|
inline |
|
inline |
| x | A kvector |
| y | A kvector of the same type of x |
Definition at line 1639 of file KVector.hpp.
|
inline |
| x | A Matrix3d |
| y | A Matrix3d of the same type of x |
Definition at line 5406 of file Matrix3d.hpp.
|
inline |
| x | A Monomial |
| y | A Monomial of the same type of x |
Definition at line 295 of file MultivariatePolynomial.hpp.
|
inline |
| x | A Vector |
| y | A Vector of the same type of x |
Definition at line 2208 of file Vector.hpp.
|
inline |
| x | A Polynomial |
| y | A Polynomial of the same type of x |
Definition at line 1440 of file Polynomial.hpp.
|
inline |
| x | A Signal |
| y | A Signal of the same type of x |
Definition at line 2221 of file Signal.hpp.
|
inline |
| x | A Array4d |
| y | A Array4d of the same type of x |
Definition at line 4778 of file Array4d.hpp.
|
inline |
| x | A HyperVolume |
| y | A HyperVolume of the same type of x |
Definition at line 4751 of file HyperVolume.hpp.
|
inline |
| x | A Volume |
| y | A Volume of the same type of x |
Definition at line 5725 of file Volume.hpp.
|
inline |
| x | A Array3d |
| y | A Array3d of the same type of x |
Definition at line 5284 of file Array3d.hpp.
|
inline |
| x | A Matrix4d |
| y | A Matrix4d of the same type of x |
Definition at line 4759 of file Matrix4d.hpp.
|
inline |
| x | A block2d |
| y | A block2d of the same type of x |
Definition at line 2396 of file Block2d.hpp.
|
inline |
| x | A Array2d |
| y | A Array2d of the same type of x |
Definition at line 3259 of file Array2d.hpp.
|
inline |
| x | A GrayscaleImage |
| y | A GrayscaleImage of the same type of x |
Definition at line 3733 of file GrayscaleImage.hpp.
|
inline |
| x | A Matrix |
| y | A Matrix of the same type of x |
Definition at line 4089 of file Matrix.hpp.
|
inline |
|
inline |
|
inline |
| out | output stream |
| p | DPoint to write to the output stream |
Definition at line 422 of file DPoint.hpp.
|
inline |
|
inline |
| std::ostream & slip::operator<< | ( | std::ostream & | out, |
| const block< T, N > & | b | ||
| ) |
|
inline |
| out | output stream |
| b | block4d to write to an output stream |
Definition at line 468 of file Block4d.hpp.
|
inline |
| out | output stream |
| b | block3d to write to an output stream |
Definition at line 459 of file Block3d.hpp.
|
inline |
| out | output std::ostream |
| a | Colormap to write to the output stream |
Definition at line 875 of file Colormap.hpp.
|
inline |
| std::ostream & slip::operator<< | ( | std::ostream & | out, |
| const slip::SoloffCamera< Type > & | c | ||
| ) |
| out | output stream |
| c | SoloffCamera to write to the output stream |
Definition at line 715 of file SoloffCamera.hpp.
| std::ostream & slip::operator<< | ( | std::ostream & | out, |
| const PinholeDLTCamera< Type > & | c | ||
| ) |
Definition at line 208 of file PinholeDLTCamera.hpp.
| std::ostream & slip::operator<< | ( | std::ostream & | out, |
| const PinholeFaugerasCamera< Type > & | c | ||
| ) |
Definition at line 211 of file PinholeFaugerasCamera.hpp.
| std::ostream & slip::operator<< | ( | std::ostream & | out, |
| const PinholeCamera< Type > & | c | ||
| ) |
| out | output stream. |
| c | PinholeCamera to write to the output stream |
Definition at line 544 of file PinholeCamera.hpp.
| std::ostream & slip::operator<< | ( | std::ostream & | out, |
| const kvector< T, N > & | b | ||
| ) |
| out | output std::ostream |
| b | kvector to write to an output stream |
Definition at line 1293 of file KVector.hpp.
|
inline |
| out | output std:ostream |
| v | Polynomial to write to the output stream |
Definition at line 956 of file Polynomial.hpp.
|
inline |
Definition at line 257 of file MultivariatePolynomial.hpp.
|
inline |
| out | output std:ostream |
| v | Vector to write to the output stream |
Definition at line 1673 of file Vector.hpp.
|
inline |
| out | output std::ostream |
| a | Matrix3d to write to the output stream |
Definition at line 5258 of file Matrix3d.hpp.
|
inline |
| out | output std:ostream |
| v | Signal to write to the output stream |
Definition at line 1687 of file Signal.hpp.
|
inline |
| out | output std::ostream |
| a | Array4d to write to the output stream |
Definition at line 4592 of file Array4d.hpp.
|
inline |
| out | output std::ostream |
| a | HyperVolume to write to the output stream |
Definition at line 4599 of file HyperVolume.hpp.
|
inline |
| out | output std::ostream |
| a | Array3d to write to the output stream |
Definition at line 5109 of file Array3d.hpp.
|
inline |
| out | output std::ostream |
| a | Volume to write to the output stream |
Definition at line 5342 of file Volume.hpp.
|
inline |
| out | output std::ostream |
| a | Matrix4d to write to the output stream |
Definition at line 4607 of file Matrix4d.hpp.
|
inline |
| out | output std::ostream |
| b | block2d to write to an output stream |
Definition at line 2356 of file Block2d.hpp.
|
inline |
| out | output stream |
| a | GenericMultiComponent3d to write to the output stream |
Definition at line 7552 of file GenericMultiComponent3d.hpp.
|
inline |
| out | output stream |
| a | GenericMultiComponent4d to write to the output stream |
Definition at line 7312 of file GenericMultiComponent4d.hpp.
|
inline |
| out | output stream |
| a | GenericMultiComponent2d to write to the output stream |
Definition at line 4760 of file GenericMultiComponent2d.hpp.
|
inline |
| out | output stream |
| a | RegularVector3dField3d to write to the output stream |
Definition at line 2478 of file RegularVector3dField3d.hpp.
|
inline |
| out | output stream |
| a | RegularVector2dField2d to write to the output stream |
Definition at line 1877 of file RegularVector2dField2d.hpp.
|
inline |
| out | output std::ostream |
| a | Array2d to write to the output stream |
Definition at line 3023 of file Array2d.hpp.
|
inline |
| out | output stream |
| a | GrayscaleImage to write to the output stream |
Definition at line 3205 of file GrayscaleImage.hpp.
|
inline |
| out | output std::ostream |
| a | Matrix to write to the output stream |
Definition at line 3409 of file Matrix.hpp.
| std::ostream & slip::operator<< | ( | std::ostream & | out, |
| const DistortionCamera< Type > & | c | ||
| ) |
| out | output stream. |
| c | PinholeCamera to write to the output stream. |
Definition at line 582 of file DistortionCamera.hpp.
|
inline |
| out | output std:ostream |
| v | MultivariatePolynomial to write to the output stream |
Definition at line 1063 of file MultivariatePolynomial.hpp.
|
inline |
| out | output std::ostream |
| a | Pyramid to write to the output stream |
Definition at line 868 of file Pyramid.hpp.
|
inline |
Definition at line 1099 of file MultivariatePolynomial.hpp.
|
inline |
Definition at line 1129 of file MultivariatePolynomial.hpp.
|
inline |
Definition at line 1158 of file MultivariatePolynomial.hpp.
|
inline |
| x | first Vector4d to compare |
| y | second Vector4d to compare return true if ||x|| <= ||y||, ||.|| is the Euclidean norm |
Definition at line 519 of file Vector4d.hpp.
|
inline |
| x | first Vector3d to compare |
| y | second Vector3d to compare return true if ||x|| <= ||y||, ||.|| is the Euclidean norm |
Definition at line 501 of file Vector3d.hpp.
|
inline |
| x | first Vector2d to compare |
| y | second Vector2d to compare return true if ||x|| <= ||y||, ||.|| is the Euclidean norm |
Definition at line 493 of file Vector2d.hpp.
|
inline |
Definition at line 540 of file Block4d.hpp.
|
inline |
Definition at line 531 of file Block3d.hpp.
|
inline |
|
inline |
|
inline |
| x | A kvector |
| y | A kvector of the same type of x |
Definition at line 1657 of file KVector.hpp.
|
inline |
| x | A Matrix3d |
| y | A Matrix3d of the same type of x |
Definition at line 5424 of file Matrix3d.hpp.
|
inline |
| x | A Polynomial |
| y | A Polynomial of the same type of x |
Definition at line 1456 of file Polynomial.hpp.
|
inline |
| x | A Vector |
| y | A Vector of the same type of x |
Definition at line 2224 of file Vector.hpp.
|
inline |
| x | A Signal |
| y | A Signal of the same type of x |
Definition at line 2237 of file Signal.hpp.
|
inline |
| x | A Array4d |
| y | A Array4d of the same type of x |
Definition at line 4796 of file Array4d.hpp.
|
inline |
| x | A HyperVolume |
| y | A HyperVolume of the same type of x |
Definition at line 4769 of file HyperVolume.hpp.
|
inline |
| x | A Volume |
| y | A Volume of the same type of x |
Definition at line 5743 of file Volume.hpp.
|
inline |
| x | A Array3d |
| y | A Array3d of the same type of x |
Definition at line 5302 of file Array3d.hpp.
|
inline |
| x | A Matrix4d |
| y | A Matrix4d of the same type of x |
Definition at line 4777 of file Matrix4d.hpp.
|
inline |
| x | A block2d |
| y | A block2d of the same type of x |
Definition at line 2413 of file Block2d.hpp.
|
inline |
| x | A Array2d |
| y | A Array2d of the same type of x |
Definition at line 3277 of file Array2d.hpp.
|
inline |
| x | A GrayscaleImage |
| y | A GrayscaleImage of the same type of x |
Definition at line 3752 of file GrayscaleImage.hpp.
|
inline |
| x | A Matrix |
| y | A Matrix of the same type of x |
Definition at line 4106 of file Matrix.hpp.
|
inline |
|
inline |
|
inline |
Definition at line 483 of file Block4d.hpp.
|
inline |
|
inline |
|
inline |
Definition at line 474 of file Block3d.hpp.
|
inline |
| x | A Colormap |
| y | A Colormap of the same type of x |
Definition at line 1007 of file Colormap.hpp.
|
inline |
| x | A kvector |
| y | A kvector of the same type of x |
Definition at line 1621 of file KVector.hpp.
|
inline |
| x | A Polynomial |
| y | A Polynomial of the same type of x |
Definition at line 1422 of file Polynomial.hpp.
|
inline |
| x | A Vector |
| y | A Vector of the same type of x |
Definition at line 2190 of file Vector.hpp.
|
inline |
| x | A Monomial |
| y | A Monomial of the same type of x |
Definition at line 275 of file MultivariatePolynomial.hpp.
|
inline |
| x | A Matrix3d |
| y | A Matrix3d of the same type of x |
Definition at line 5385 of file Matrix3d.hpp.
|
inline |
| x | A Signal |
| y | A Signal of the same type of x |
Definition at line 2203 of file Signal.hpp.
|
inline |
| x | A Array4d |
| y | A Array4d of the same type of x |
Definition at line 4759 of file Array4d.hpp.
|
inline |
| x | A HyperVolume |
| y | A HyperVolume of the same type of x |
Definition at line 4730 of file HyperVolume.hpp.
|
inline |
| x | A Volume |
| y | A Volume of the same type of x |
Definition at line 5704 of file Volume.hpp.
|
inline |
| x | A Array3d |
| y | A Array3d of the same type of x |
Definition at line 5265 of file Array3d.hpp.
|
inline |
| x | A Matrix4d |
| y | A Matrix4d of the same type of x |
Definition at line 4738 of file Matrix4d.hpp.
|
inline |
| x | A GenericMultiComponent3d |
| y | A GenericMultiComponent3d of the same type of x |
Definition at line 7688 of file GenericMultiComponent3d.hpp.
|
inline |
| x | A block2d |
| y | A block2d of the same type of x |
Definition at line 2375 of file Block2d.hpp.
|
inline |
| x | A GenericMultiComponent4d |
| y | A GenericMultiComponent4d of the same type of x |
Definition at line 7349 of file GenericMultiComponent4d.hpp.
|
inline |
| x | A GenericMultiComponent2d |
| y | A GenericMultiComponent2d of the same type of x |
Definition at line 4927 of file GenericMultiComponent2d.hpp.
|
inline |
| x | A Array2d |
| y | A Array2d of the same type of x |
Definition at line 3238 of file Array2d.hpp.
|
inline |
| x | A GrayscaleImage |
| y | A GrayscaleImage of the same type of x |
Definition at line 3713 of file GrayscaleImage.hpp.
|
inline |
| x | A Matrix |
| y | A Matrix of the same type of x |
Definition at line 4068 of file Matrix.hpp.
| bool slip::operator== | ( | const Pyramid< Container > & | x, |
| const Pyramid< Container > & | y | ||
| ) |
Definition at line 885 of file Pyramid.hpp.
|
inline |
| x | first Vector4d to compare |
| y | second Vector4d to compare return true if ||x|| > ||y||, ||.|| is the Euclidean norm |
Definition at line 511 of file Vector4d.hpp.
|
inline |
| x | first Vector3d to compare |
| y | second Vector3d to compare return true if ||x|| > ||y||, ||.|| is the Euclidean norm |
Definition at line 493 of file Vector3d.hpp.
|
inline |
| x | first Vector2d to compare |
| y | second Vector2d to compare return true if ||x|| > ||y||, ||.|| is the Euclidean norm |
Definition at line 485 of file Vector2d.hpp.
|
inline |
Definition at line 526 of file Block4d.hpp.
|
inline |
Definition at line 517 of file Block3d.hpp.
|
inline |
|
inline |
|
inline |
| x | A kvector |
| y | A kvector of the same type of x |
Definition at line 1648 of file KVector.hpp.
|
inline |
| x | A Polynomial |
| y | A Polynomial of the same type of x |
Definition at line 1448 of file Polynomial.hpp.
|
inline |
| x | A Vector |
| y | A Vector of the same type of x |
Definition at line 2216 of file Vector.hpp.
|
inline |
| x | A Monomial |
| y | A Monomial of the same type of x |
Definition at line 306 of file MultivariatePolynomial.hpp.
|
inline |
| x | A Matrix3d |
| y | A Matrix3d of the same type of x |
Definition at line 5416 of file Matrix3d.hpp.
|
inline |
| x | A Signal |
| y | A Signal of the same type of x |
Definition at line 2229 of file Signal.hpp.
|
inline |
| x | A Array4d |
| y | A Array4d of the same type of x |
Definition at line 4788 of file Array4d.hpp.
|
inline |
| x | A HyperVolume |
| y | A HyperVolume of the same type of x |
Definition at line 4761 of file HyperVolume.hpp.
|
inline |
| x | A Volume |
| y | A Volume of the same type of x |
Definition at line 5735 of file Volume.hpp.
|
inline |
| x | A Array3d |
| y | A Array3d of the same type of x |
Definition at line 5294 of file Array3d.hpp.
|
inline |
| x | A Matrix4d |
| y | A Matrix4d of the same type of x |
Definition at line 4769 of file Matrix4d.hpp.
|
inline |
| x | A block2d |
| y | A block2d of the same type of x |
Definition at line 2405 of file Block2d.hpp.
|
inline |
| x | A Array2d |
| y | A Array2d of the same type of x |
Definition at line 3269 of file Array2d.hpp.
|
inline |
| x | A GrayscaleImage |
| y | A GrayscaleImage of the same type of x |
Definition at line 3743 of file GrayscaleImage.hpp.
|
inline |
| x | A Matrix |
| y | A Matrix of the same type of x |
Definition at line 4098 of file Matrix.hpp.
|
inline |
Definition at line 509 of file Vector3d.hpp.
|
inline |
Definition at line 527 of file Vector4d.hpp.
|
inline |
Definition at line 501 of file Vector2d.hpp.
|
inline |
Definition at line 554 of file Block4d.hpp.
|
inline |
Definition at line 545 of file Block3d.hpp.
|
inline |
|
inline |
|
inline |
| x | A kvector |
| y | A kvector of the same type of x |
Definition at line 1666 of file KVector.hpp.
|
inline |
| x | A Matrix3d |
| y | A Matrix3d of the same type of x |
Definition at line 5432 of file Matrix3d.hpp.
|
inline |
| x | A Vector |
| y | A Vector of the same type of x |
Definition at line 2232 of file Vector.hpp.
|
inline |
| x | A Polynomial |
| y | A Polynomial of the same type of x |
Definition at line 1464 of file Polynomial.hpp.
|
inline |
| x | A Array4d |
| y | A Array4d of the same type of x |
Definition at line 4804 of file Array4d.hpp.
|
inline |
| x | A Signal |
| y | A Signal of the same type of x |
Definition at line 2245 of file Signal.hpp.
|
inline |
| x | A HyperVolume |
| y | A HyperVolume of the same type of x |
Definition at line 4777 of file HyperVolume.hpp.
|
inline |
| x | A Volume |
| y | A Volume of the same type of x |
Definition at line 5751 of file Volume.hpp.
|
inline |
| x | A Array3d |
| y | A Array3d of the same type of x |
Definition at line 5310 of file Array3d.hpp.
|
inline |
| x | A Matrix4d |
| y | A Matrix4d of the same type of x |
Definition at line 4785 of file Matrix4d.hpp.
|
inline |
| x | A block2d |
| y | A block2d of the same type of x |
Definition at line 2421 of file Block2d.hpp.
|
inline |
| x | A Array2d |
| y | A Array2d of the same type of x |
Definition at line 3285 of file Array2d.hpp.
|
inline |
| x | A GrayscaleImage |
| y | A GrayscaleImage of the same type of x |
Definition at line 3761 of file GrayscaleImage.hpp.
|
inline |
| x | A Matrix |
| y | A Matrix of the same type of x |
Definition at line 4114 of file Matrix.hpp.
|
inline |
Definition at line 1081 of file derivatives.hpp.
|
inline |
Definition at line 1068 of file derivatives.hpp.
|
inline |
Computes the hermitian outer product of the vector V and the transpose of the conjugate of the vector W:
![\[ R = V \times W^{H} \]](../../form_81.png)
.
| V_begin | iterator on the first element of V |
| V_end | iterator on the last element of V |
| W_begin | iterator on the first element of W |
| W_end | iterator on the last element of W |
| R_up | 2d iterator on the upper_left element of the result matrix |
| R_bot | 2d iterator on the bottom_right element of the result matrix |
Definition at line 2739 of file linear_algebra.hpp.
|
inline |
Returns the partial pivot of a 2d range.
| M_up | 2D iterator on the upper_left element of M container |
| M_bot | 2D iterator on the bottom_right element of M container |
Definition at line 4909 of file linear_algebra.hpp.
|
inline |
|
inline |
Get uniform metric for PCA computation.
| data | container of all datas |
| centerdata | container of all centered datas |
| normalize_data | Need to normalize data dividing by stddev or not ? |
|
inline |
Compute the PCA (data need to be centered)
| data | container of all datas (prefered centered data) |
| acp | ACP result matrix |
| metric | Metric used |
| eigenval | Vector of Eigen values of the variance covariance matrix |
|
inline |
Data reduction using ACP.
| data | container of all datas |
| metric | Metric used |
| result | result container |
| nbaxis | Number of axis needed |
| normalize_data | Normalize initial data dividing by stddev ? |
|
inline |
Data reduction using ACP.
| data | container of all datas |
| metric | Metric used |
| result | result container (size define the data reduction) |
| normalize_data | Normalize initial data dividing by stddev ? |
|
inline |
|
inline |
|
inline |
Pseudo inverse of a matrix.
| A | matrix to invert. |
| Ainv | inverted matrix. |
Definition at line 1274 of file linear_algebra_svd.hpp.
|
inline |
Returns the row position of the maximum partial pivot of a 2d range.
| M_up | 2D iterator on the upper_left element of M container |
| M_bot | 2D iterator on the bottom_right element of M container |
Definition at line 4877 of file linear_algebra.hpp.
| int slip::plt_get_file_type | ( | std::ifstream & | fp | ) |
Read a binary tecplot file, move the stream pointer and return header informations.
| fp | Input stream to the file path name. |
Definition at line 224 of file tecplot_binaries.hpp.
| int slip::plt_get_file_type | ( | const std::string & | file_path_name | ) |
Read a binary tecplot file, move the stream pointer and return header informations.
| fp | Input stream to the file path name. |
Definition at line 289 of file tecplot_binaries.hpp.
| int slip::plt_get_order | ( | std::ifstream & | fp | ) |
Read a binary tecplot file, move the stream pointer and return header informations.
| fp | Input stream to the file path name. |
Definition at line 145 of file tecplot_binaries.hpp.
| int slip::plt_get_order | ( | const std::string & | file_path_name | ) |
Read a binary tecplot file, move the stream pointer and return header informations.
| fp | Input stream to the file path name. |
Definition at line 188 of file tecplot_binaries.hpp.
| void slip::plt_read_header | ( | std::ifstream & | fp, |
| int & | NbVars, | ||
| int & | NbZones, | ||
| int & | K, | ||
| int & | I, | ||
| int & | J, | ||
| std::string & | title, | ||
| std::string & | zonename, | ||
| std::vector< std::string > & | varnames, | ||
| double & | SolTime, | ||
| int | NumZone = 1 |
||
| ) |
Read a binary tecplot file, move the stream pointer and return header informations.
| fp | Input stream to the file path name. |
| NbVars | Number of variables. |
| NbZones | Number of zones. |
| K | Number of slices. |
| I | Number of rows. |
| J | Number of cols. |
| title | String for the frame title. |
| title | String for the zone name. |
| varnames | Vector containing the variable names. |
| SolTime | Solution Time. |
Definition at line 330 of file tecplot_binaries.hpp.
| void slip::plt_read_header | ( | std::ifstream & | fp, |
| int & | NbVars, | ||
| int & | NbZones, | ||
| int & | K, | ||
| int & | I, | ||
| int & | J, | ||
| int | NumZone = 1 |
||
| ) |
Read a binary tecplot file and return header informations.
| fp | Input stream to the file. |
| NbVars | Number of variables. |
| NbZones | Number of zones. |
| K | Number of slices. |
| I | Number of rows. |
| J | Number of cols. |
| NumZone | Index of the zone for which the I, J and K are extracted. This parameter is optional and the first zone is extracted by default. |
Definition at line 672 of file tecplot_binaries.hpp.
| void slip::plt_read_header | ( | const std::string & | file_path_name, |
| int & | NbVars, | ||
| int & | NbZones, | ||
| int & | K, | ||
| int & | I, | ||
| int & | J, | ||
| int | NumZone = 1 |
||
| ) |
Read a binary tecplot file and return header informations.
| file_path_name | String of the file path name. |
| NbVars | Number of variables. |
| NbZones | Number of zones. |
| K | Number of slices. |
| I | Number of rows. |
| J | Number of cols. |
| NumZone | Index of the zone for which the I, J and K are extracted. This parameter is optional and the first zone is extracted by default. |
Definition at line 703 of file tecplot_binaries.hpp.
| void slip::plt_read_header | ( | const std::string & | file_path_name, |
| int & | NbVars, | ||
| int & | NbZones, | ||
| int & | K, | ||
| int & | I, | ||
| int & | J, | ||
| double & | SolTime, | ||
| int | NumZone = 1 |
||
| ) |
Read a binary tecplot file and return header informations.
| file_path_name | String of the file path name. |
| NbVars | Number of variables. |
| NbZones | Number of zones. |
| K | Number of slices. |
| I | Number of rows. |
| J | Number of cols. |
| SolTime | Solution time. |
| NumZone | Index of the zone for which the I, J and K are extracted. This parameter is optional and the first zone is extracted by default. |
Definition at line 738 of file tecplot_binaries.hpp.
| void slip::plt_read_header | ( | const std::string & | file_path_name, |
| int & | NbVars, | ||
| int & | NbZones, | ||
| int & | K, | ||
| int & | I, | ||
| int & | J, | ||
| std::string & | title, | ||
| std::string & | zonename, | ||
| std::vector< std::string > & | varnames, | ||
| double & | SolTime, | ||
| int | NumZone = 1 |
||
| ) |
Read a binary tecplot file and return header informations.
| file_path_name | String of the file path name. |
| NbVars | Number of variables. |
| NbZones | Number of zones. |
| K | Number of slices. |
| I | Number of rows. |
| J | Number of cols. |
| SolTime | Solution time. |
| NumZone | Index of the zone for which the I, J and K are extracted. This parameter is optional and the first zone is extracted by default. |
Definition at line 778 of file tecplot_binaries.hpp.
| void slip::plt_to_Array2d | ( | const std::string & | file_path_name, |
| Container2d & | reg, | ||
| const int | zone_loaded = 1 |
||
| ) |
Read a binary tecplot file and put the data in a 2d container.
| file_path_name | String of the file path name. |
| reg | Container2d for the read data. |
| zone_loaded | Zone index to read (1 by default). |
Definition at line 803 of file tecplot_binaries.hpp.
| void slip::plt_to_RegularVector2dField2d | ( | const std::string & | file_path_name, |
| RegularVector2dField2d & | reg, | ||
| std::string & | title, | ||
| std::string & | zonename, | ||
| std::vector< std::string > & | varnames, | ||
| const int | zone_loaded = 1 |
||
| ) |
Read a slip::RegularVector2dField2d from a binary tecplot file.
| file_path_name | String of the file path name. |
| reg | slip::RegularVector2dField2d container. |
| title | Title of the tecplot frame. |
| zone | Name of the tecplot zone. |
| varnames | Vector containing the variable names. |
| zone_loaded | Zone index to read (1 by default). |
Definition at line 2003 of file tecplot_binaries.hpp.
| void slip::plt_to_RegularVector2dField2d | ( | const std::string & | file_path_name, |
| RegularVector2dField2d & | reg, | ||
| const int | zone_loaded = 1 |
||
| ) |
Read a slip::RegularVector2dField2d from a binary tecplot file.
| file_path_name | String of the file path name. |
| reg | slip::RegularVector2dField2d container. |
| zone_loaded | Zone index to read (1 by default). |
Definition at line 2292 of file tecplot_binaries.hpp.
| void slip::plt_to_RegularVector3dField3d | ( | const std::string & | file_path_name, |
| RegularVector3dField3d & | reg, | ||
| std::string & | title, | ||
| std::string & | zonename, | ||
| std::vector< std::string > & | varnames, | ||
| const int | zone_loaded = 1 |
||
| ) |
Read a slip::RegularVector3dField3d from a binary tecplot file.
| file_path_name | String of the file path name. |
| reg | slip::RegularVector3dField3d container. |
| title | Title of the tecplot frame. |
| zonename | Name of the tecplot zone. |
| varnames | Name of all the variables. |
| zone_loaded | Zone index to read (1 by default). |
Definition at line 990 of file tecplot_binaries.hpp.
| void slip::plt_to_RegularVector3dField3d | ( | const std::string & | file_path_name, |
| RegularVector3dField3d & | reg, | ||
| const int | zone_loaded = 1 |
||
| ) |
Read a slip::RegularVector3dField3d from a binary tecplot file.
| file_path_name | String of the file path name. |
| reg | slip::RegularVector3dField3d container. |
| zone_loaded | Zone index to read (1 by default). |
Definition at line 1298 of file tecplot_binaries.hpp.
|
inline |
Computes the addition of two ranges.
| __first1 | An InputIterator. |
| __last1 | An InputIterator. |
| __first2 | An InputIterator. |
| __result | An OutputIterator. |
Definition at line 125 of file arithmetic_op.hpp.
|
inline |
Computes the addition of two ranges according to a Predicate.
| __first1 | An input iterator. |
| __last1 | An input iterator. |
| __first2 | An input iterator. |
| __result | An output iterator. |
| __pred | A predicate. |
Definition at line 267 of file arithmetic_op.hpp.
|
inline |
Computes the addition of two ranges according to a mask sequence.
| __first1 | An input iterator. |
| __last1 | An input iterator. |
| __mask_first | An input iterator. |
| __first2 | An input iterator. |
| __result | An output iterator. |
| value | true value of the mask range. Default is 1. |
Definition at line 202 of file arithmetic_op.hpp.
|
inline |
Adds a scalar to a range.
| __first1 | An InputIterator. |
| __last1 | An InputIterator. |
| scalar | A scalar value. |
| __result | An OutputIterator. |
Definition at line 1269 of file arithmetic_op.hpp.
|
inline |
Adds a scalar to a range according to a Predicate.
| __first1 | An input iterator. |
| __last1 | An input iterator. |
| scalar | A scalar value. |
| __result | An output iterator. |
| __pred | A predicate. |
Definition at line 1393 of file arithmetic_op.hpp.
|
inline |
Adds a scalar to a range according to a mask sequence.
| __first1 | An input iterator. |
| __last1 | An input iterator. |
| __mask_first | An input iterator. |
| scalar | A scalar value. |
| __result | An output iterator. |
| value | true value of the mask range. Default is 1. |
Definition at line 1335 of file arithmetic_op.hpp.
|
inline |
Computes the pseudo normalized crosscorrelation between two sequences: 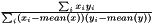 .
.
| first | An InputIterator. |
| last | An InputIterator. |
| first2 | An InputIterator. |
| mean1 | mean value of the first range [first,last). |
| mean2 | mean value of the second range [first2, first2 + (last-first)). |
Definition at line 1022 of file correlation.hpp.
|
inline |
Computes the standard pseudo normalized crosscorrelation between two sequences according to a Predicate. 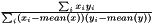 .
.
| first1 | An InputIterator. |
| last1 | An InputIterator. |
| first2 | An InputIterator. |
| pred | A predicate. |
| mean1 | mean value of the first range [first,last). |
| mean2 | mean value of the second range [first2, first2 + (last-first)). |
Definition at line 1120 of file correlation.hpp.
|
inline |
Computes the pseudo normalized crosscorrelation between two sequences according to a mask sequence : 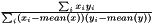 .
.
| first1 | An InputIterator. |
| last1 | An InputIterator. |
| mask_first | An InputIterator. |
| first2 | An InputIterator. |
| mean1 | mean value of the first range [first,last). |
| mean2 | mean value of the second range [first2, first2 + (last-first)). |
| value | true value of the mask range. Default is 1. |
Definition at line 1069 of file correlation.hpp.
|
inline |
function to compute.
| x | The element to power |
| N | The power. |
Definition at line 368 of file macros.hpp.
| void slip::print | ( | const Container & | C, |
| const std::string & | name = "" |
||
| ) |
Print the name of the container follow by the values of the container in a terminal.
| C | Container to print. |
| name | Name of the container to print |
Definition at line 246 of file io_tools.hpp.
|
inline |
Computes the pseudo normalized crosscorrelation between two sequences: 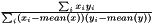 .
.
| first | An InputIterator. |
| last | An InputIterator. |
| first2 | An InputIterator. |
| mean1 | mean value of the first range [first,last). |
| mean2 | mean value of the second range [first2, first2 + (last-first)). |
Definition at line 828 of file correlation.hpp.
|
inline |
Computes the pseudo normalized crosscorrelation between two Images.
| in1_upper_left | : A 2d input iterator (image). |
| in1_bottom_right | : A 2d input iterator (image). |
| in2_upper_left | : A 2d input iterator (mask). |
| in2_bottom_right | : A 2d input iterator (mask). |
| out_upper_left | : A 2d output iterator (result). |
| out_bottom_right | : A 2d output iterator (result). |
Definition at line 2178 of file correlation.hpp.
|
inline |
Computes the standard pseudo normalized crosscorrelation between two sequences according to a Predicate. 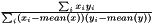 .
.
| first1 | An InputIterator. |
| last1 | An InputIterator. |
| first2 | An InputIterator. |
| pred | A predicate. |
| mean1 | mean value of the first range [first,last). |
| mean2 | mean value of the second range [first2, first2 + (last-first)). |
Definition at line 947 of file correlation.hpp.
|
inline |
Computes the pseudo normalized crosscorrelation between two sequences according to a mask sequence : 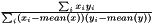 .
.
| first1 | An InputIterator. |
| last1 | An InputIterator. |
| mask_first | An InputIterator. |
| first2 | An InputIterator. |
| mean1 | mean value of the first range [first,last). |
| mean2 | mean value of the second range [first2, first2 + (last-first)). |
| value | true value of the mask range. Default is 1. |
Definition at line 883 of file correlation.hpp.
|
inline |
| first1 | An InputIterator. |
| last1 | An InputIterator. |
| first2 | An InputIterator. for the second datas |
Definition at line 2067 of file compare.hpp.
|
inline |
| first1 | An InputIterator. |
| last1 | An InputIterator. |
| first2 | An InputIterator. |
| pred | A predicate |
Definition at line 2163 of file compare.hpp.
|
inline |
| first1 | An InputIterator. |
| last1 | An InputIterator. |
| mask1 | An InputIterator. |
| first2 | An InputIterator. |
| value | An value corresponding to the mask |
Definition at line 2112 of file compare.hpp.
|
inline |
Computes 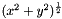 without destructive underflow or overflow.
without destructive underflow or overflow.
| x | first value |
| y | second value |
Definition at line 289 of file macros.hpp.
|
inline |
Computes the Cooley-Tukey (radix2) fft of a container.
| a | A BidirectionalIterator to iterate throw the input data |
| b | A BidirectionalIterator to iterate throw the output data |
| log2n | Corresponds to log2(size(a)). |
|
inline |
Computes the radix 2 fft2d of a container with 1d iterator (compatible with simple pointers).
| begin1 | The begin iterator of the first container |
| begin2 | The begin iterator of the second container |
| nb_lig | The number of rows |
| nb_col | The number of columns |
|
inline |
Computes the radix2 (Cooley-Tukey) fft2d of a container with 2d iterators.
| in_upper_left | |
| in_bottom_right | |
| out_upper_left |
|
inline |
Computes the radix2 fft2d of a container.
| datain | The input datas |
| dataout | The output datas |
|
inline |
Computes the inverse Cooley-Tukey (radix2) fft of a container.
| a | A BidirectionalIterator to iterate throw the input data |
| b | A BidirectionalIterator to iterate throw the output data |
| log2n | Corresponds to log2(size(a)). |
|
inline |
Computes the inverse radix 2 fft2d of a container with 1d iterators (compatible with simple pointers).
| begin1 | The begin iterator of the first container |
| begin2 | The begin iterator of the second container |
| nb_lig | The number of rows |
| nb_col | The number of columns |
|
inline |
Computes the radix2 ifft2d of a container with 2d iterators.
| in_upper_left | |
| in_bottom_right | |
| out_upper_left |
|
inline |
Computes the radix2 fft2d of a container.
| datain | The input datas |
| dataout | The output datas |
| void slip::rank1_tensorial_product | ( | RandomAccessIterator1 | base1_first, |
| RandomAccessIterator1 | base1_end, | ||
| RandomAccessIterator2 | base2_first, | ||
| RandomAccessIterator2 | base2_end, | ||
| RandomAccessIterator2d | matrix_upper_left, | ||
| RandomAccessIterator2d | matrix_bottom_right | ||
| ) |
Computes the tensorial product of two rank one tensors 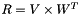 it provides a rank2 tensor (Container2d) of size (MxN) if M and N are respectivly the size of V and W.
it provides a rank2 tensor (Container2d) of size (MxN) if M and N are respectivly the size of V and W.
| base1_first | iterator on the first element of the first rank one tensor |
| base1_end | iterator on one-past-the-end element of the first rank one tensor |
| base2_first | iterator on the first element of the second rank one tensor |
| base2_end | iterator on one-past-the-end element of the second rank one tensor |
| matrix_upper_left | 2d iterator on the first element of the rank two tensor |
| matrix_bottom_right | 2d iterator on the one-past-the-end element of the rank two tensor |
Definition at line 2859 of file linear_algebra.hpp.
| void slip::rank1_tensorial_product | ( | RandomAccessIterator1 | base1_first, |
| RandomAccessIterator1 | base1_end, | ||
| RandomAccessIterator2 | base2_first, | ||
| RandomAccessIterator2 | base2_end, | ||
| RandomAccessIterator3 | base3_first, | ||
| RandomAccessIterator3 | base3_end, | ||
| RandomAccessIterator3d | base_front_upper_left, | ||
| RandomAccessIterator3d | base_back_bottom_right | ||
| ) |
Computes the tensorial product of three rank one tensors it provides a rank3 tensor (Container3d) of size (PxMxN) if P, M and N are respectivly the size of V, W and X.
| base1_first | iterator on the first element of the first rank one tensor |
| base1_end | iterator on one-past-the-end element of the first rank one tensor |
| base2_first | iterator on the first element of the second rank one tensor |
| base2_end | iterator on one-past-the-end element of the second rank one tensor |
| base3_first | iterator on the first element of the third rank one tensor |
| base3_end | iterator on one-past-the-end element of the third rank one tensor |
| base_front_upper_left | 3d iterator on the first element of the rank three tensor |
| base_back_bottom_right | 3d iterator on the one-past-the-end element of the rank three tensor |
Definition at line 3037 of file linear_algebra.hpp.
|
inline |
Computes
![\[ A = A + \alpha X Y^H\]](../../form_75.png)
.
| A_up | RandomAccessIterator2d to the upper_left matrix element. |
| A_bot | RandomAccessIterator2d to the bottom_right matrix element. |
| alpha | Scalar. |
| X_first | RandomAccessIterator to the first element of the vector X. |
| X_last | RandomAccessIterator to one-past-the-end element of the vector X. |
| Y_first | RandomAccessIterator to the first element of the vector Y. |
| Y_last | RandomAccessIterator to one-past-the-end element of the vector Y. |
Definition at line 2346 of file linear_algebra.hpp.
|
inline |
Computes
![\[ A = A + \alpha X Y^H\]](../../form_75.png)
.
| A | Matrix A. |
| alpha | Scalar. |
| X | The vector X. |
| Y | The vector Y. |
Definition at line 2421 of file linear_algebra.hpp.
|
inline |
Computes the rayleigh coefficient of a vector x:
![\[ r(x) = \frac{x^H A x}{x^Hx} \]](../../form_62.png)
.
| first1 | RandomAccessIterator to the first element of the vector x. |
| last1 | RandomAccessIterator to one-past-the-end element of the vector x. |
| A_upper_left | RandomAccessIterator2d to the upper_left matrix element. |
| A_bottom_right | RandomAccessIterator2d to the bottom_right matrix element. |
Definition at line 557 of file linear_algebra.hpp.
|
inline |
Computes the rayleigh coefficient o f a vector x:
![\[ r(x) = \frac{x^H A x}{x^Hx} \]](../../form_62.png)
.
| X | The vector x. |
| A | The matrix A. |
Definition at line 603 of file linear_algebra.hpp.
|
inline |
Read a Container1d from an ASCII file.
| file_path_name | String of the file path name |
| container | Container 1d. |
Definition at line 2518 of file io_tools.hpp.
|
inline |
Read a Container2d from an ASCII file.
| container | 2d container to read. |
| file_path_name | String of the file path name |
Definition at line 544 of file io_tools.hpp.
|
inline |
Create a DenseVector2dField2D from a gnuplot file.
| file_path_name | String of the file path name |
| field | DenseVector2dField2D. |
Definition at line 1521 of file io_tools.hpp.
|
inline |
Create a DenseVector2dField2D from a gnuplot file handle 2d real regular grid.
| file_path_name | String of the file path name |
| field | DenseVector2dField2D. |
| init_point | Point2d corresponding to the point having the smallest x and y coordinates. |
| step | Steps of the regular grid. |
Definition at line 1563 of file io_tools.hpp.
|
inline |
Create a XY DenseVector2dField2D from a gnuplot file.
| file_path_name | String of the file path name |
| XY | DenseVector2dField2D which store the XY locations. |
Definition at line 1604 of file io_tools.hpp.
|
inline |
Read X and Y column of a 2d gnuplot ASCII file.
| file_path_name | String of the file path name |
| X | Container 1d containing X part of tecplot file. |
| Y | Container 1d containing Y part of tecplot file. |
Definition at line 1642 of file io_tools.hpp.
|
inline |
Create a XYZ DenseVector3dField3D from a gnuplot file.
| file_path_name | String of the file path name. |
| XYZ | DenseVector3dField3D. |
Definition at line 2437 of file io_tools.hpp.
|
inline |
Write a Container to an raw file.
| file_path_name | String of the file path name |
| first | InputIterator. |
| last | InputIterator. |
Definition at line 345 of file io_tools.hpp.
|
inline |
Create a DenseVector2dField2D from a tecplot file.
| file_path_name | String of the file path name |
| field | DenseVector2dField2D. |
Definition at line 1080 of file io_tools.hpp.
|
inline |
Create a DenseVector2dField2D from a tecplot file handle 2d real regular grid.
| file_path_name | String of the file path name |
| field | DenseVector2dField2D. |
| init_point | Point2d corresponding to the point having the smallest x and y coordinates. |
| step | step between element of the grid. |
Definition at line 1192 of file io_tools.hpp.
|
inline |
Create a DenseVector3dField3D from a tecplot file.
| file_path_name | String of the file path name |
| field | DenseVector3dField3D. |
Definition at line 1860 of file io_tools.hpp.
|
inline |
Create a DenseVector3dField3D from a tecplot file handle 3d real regular grid.
| file_path_name | String of the file path name |
| field | DenseVector3dField3D. |
| init_point | Point3d corresponding to the point having the smallest x, y and z coordinates. |
| step | Point3d corresponding to the steps of the regular grid. TITLE= title
VARIABLES= X Y Z U V W
ZONE T= zone, I= rows(), J= cols(), K = slices()
x y z U(x,y,z) V(x,y,z) W(x,y,z)
|
Definition at line 2000 of file io_tools.hpp.
|
inline |
Create a XY DenseVector2dField2D from a tecplot file.
| file_path_name | String of the file path name |
| XY | DenseVector2dField2D which store the XY locations. |
Definition at line 1312 of file io_tools.hpp.
|
inline |
Reads X and Y column of an ASCII 2d tecplot file.
| file_path_name | String of the file path name |
| X | Container 1d containing X part of tecplot file. |
| Y | Container 1d containing Y part of tecplot file. |
Definition at line 1422 of file io_tools.hpp.
|
inline |
Create a XYZ DenseVector3dField3D from a tecplot file.
| file_path_name | String of the file path name |
| XYZ | DenseVector3dField3D. |
Definition at line 2153 of file io_tools.hpp.
|
inline |
Create a XYZ DenseVector3dField3D from a tecplot file.
| file_path_name | String of the file path name |
| X | Container1d containing the X locations. |
| Y | Container1d containing the Y locations. |
| Z | Container1d containing the Z locations. |
Definition at line 2295 of file io_tools.hpp.
|
inline |
Extract the real Matrix of a complex Matrix. 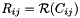 .
.
| C | Complex Matrix container |
| R | result of the real |
Definition at line 2643 of file linear_algebra.hpp.
|
inline |
Computes the real fft of a container.
| in_begin | A BidirectionalIterator to iterate throw the input data |
| in_end | A BidirectionalIterator at the end of the input data |
| out_begin | A BidirectionalIterator to iterate throw the output data |
|
inline |
Computes the real fft2d of a container with 2d iterators.
| in_upper_left | |
| in_bottom_right | |
| out_upper_left |
|
inline |
Computes the real fft2d of a container.
| datain | The input datas |
| dataout | The output datas |
|
inline |
Computes the real fft3d of a container with 3d iterators.
| in_front_upper_left | |
| in_back_bottom_right | |
| out_front_upper_left |
|
inline |
Computes the real fft3d of a container.
| datain | The input datas |
| dataout | The output datas |
|
inline |
Computes the real fft4d of a container with 4d iterators.
| in_first_front_upper_left | |
| in_last_back_bottom_right | |
| out_first_front_upper_left |
|
inline |
Computes the real fft4d of a container.
| datain | The input datas |
| dataout | The output datas |
|
inline |
Computes the real fftw of a container (from fftw3.h).
| in_begin | A BidirectionalIterator to iterate from the beginning of the input data |
| in_end | A BidirectionalIterator to iterate from the end of the input data |
| out_begin | A BidirectionalIterator to iterate from the beginning of the output data |
|
inline |
Computes the real fftw2d of a container with 2d iterators.
| in_upper_left | |
| in_bottom_right | |
| out_upper_left |
|
inline |
Computes the real fftw2d of a container.
| datain | The input datas |
| dataout | The output datas |
|
inline |
Computes the real fftw3d of a container with 3d iterators.
| in_front_upper_left | |
| in_back_bottom_right | |
| out_front_upper_left |
|
inline |
Computes the real fftw3d of a container 3d.
|
inline |
Computes the real fftw4d of a container with 4d iterators.
| in_first_front_upper_left | |
| in_last_back_bottom_right | |
| out_first_front_upper_left |
|
inline |
Computes the real fftw4d of a container 4d.
|
inline |
Complex histogram algorithm (variable step)
| first | begin iterator of the container to histogram |
| last | past-the-end iterator of the container to histogram |
| stepfirst | begin iterator of the container to steps |
| steplast | past-the-end iterator of the container to steps |
| result | begin iterator of the result container |
|
inline |
Computes the Cooley-Tukey (radix2) real_fft of a container.
| a | A BidirectionalIterator to iterate throw the input data |
| b | A BidirectionalIterator to iterate throw the output data |
| log2n | Corresponds to log2(size(a)). |
|
inline |
Computes the real split radix fft of a container (from FFTPACK.hpp).
| in_begin | A BidirectionalIterator to iterate from the beginning of the input data |
| in_end | A BidirectionalIterator to iterate from the end of the input data |
| out_begin | A BidirectionalIterator to iterate from the beginning of the output data |
|
inline |
Computes the real split-radix fft2d of a container with 2d iterators.
| in_upper_left | . |
| in_bottom_right | |
| out_upper_left |
|
inline |
Computes the real split-radix fft2d of a container.
| datain | The input datas |
| dataout | The output datas |
|
inline |
Computes the real split-radix fft3d of a container with 3d iterators.
| in_front_upper_left | |
| in_back_bottom_right | |
| out_front_upper_left |
|
inline |
Computes the real split-radix fft3d of a container 3d.
|
inline |
Computes the real split-radix fft4d of a container with 4d iterators.
| in_first_front_upper_left | input start iterator4d |
| in_last_back_bottom_right | input end interator4d |
| out_first_front_upper_left | output start iterator4d |
|
inline |
Computes the real split-radix fft4d of a container 4d.
|
inline |
Add u times the second sequence to the first one: seq1 = seq1 + u * seq2.
| seq1_beg | iterator to the beginning of the first sequence |
| seq1_end | iterator to the end of the first sequence |
| seq2_beg | iterator to the beginning of the second sequence |
| u | reduction constant |
Definition at line 2448 of file linear_algebra.hpp.
| void slip::RegularVector2dField2d_to_plt | ( | const std::string & | file_path_name, |
| RegularVector2dField2d & | reg, | ||
| std::string | title, | ||
| std::string | zone, | ||
| const double | SolTime, | ||
| std::vector< std::string > | varnames = std::vector<std::string>(), |
||
| const int | FileType = 0 |
||
| ) |
Write a slip::RegularVector2dField2d to a binary tecplot file.
| file_path_name | String of the file path name. |
| reg | slip::RegularVector2dField2d container. |
| title | Title of the tecplot frame ("Title" by default). |
| zone | Name of the tecplot zone ("Zone" by default). |
| varnames | Vector containing the variable names ("X", "Y", "U", "V" by default). |
Definition at line 2547 of file tecplot_binaries.hpp.
| void slip::RegularVector2dField2d_to_plt | ( | const std::string & | file_path_name, |
| RegularVector2dField2d & | reg, | ||
| const int | FileType = 0 |
||
| ) |
Write a slip::RegularVector2dField2d to a binary tecplot file.
| file_path_name | String of the file path name. |
| reg | slip::RegularVector2dField2d container. |
| FileType | Type of file : 0=FULL, 1=Grid only, 2=Solution only (0 by default). |
Definition at line 2804 of file tecplot_binaries.hpp.
| void slip::RegularVector2dField2d_to_plt | ( | const std::string & | file_path_name, |
| RegularVector2dField2d & | reg, | ||
| const double | SolTime, | ||
| const int | FileType = 0 |
||
| ) |
Write a slip::RegularVector2dField2d to a binary tecplot file.
| file_path_name | String of the file path name. |
| reg | slip::RegularVector2dField2d container. |
| SolTime | Solution Time. |
| FileType | Type of file : 0=FULL, 1=Grid only, 2=Solution only (0 by default). |
Definition at line 2831 of file tecplot_binaries.hpp.
| void slip::RegularVector2dField2d_to_plt | ( | const std::string & | file_path_name, |
| RegularVector2dField2d & | reg, | ||
| std::string | title, | ||
| std::string | zone, | ||
| const int | FileType = 0 |
||
| ) |
Write a slip::RegularVector2dField2d to a binary tecplot file.
| file_path_name | String of the file path name. |
| reg | slip::RegularVector2dField2d container. |
| title | Title of the tecplot frame ("Title" by default). |
| zone | Name of the tecplot zone ("Zone" by default). |
| FileType | Type of file : 0=FULL, 1=Grid only, 2=Solution only (0 by default). |
Definition at line 2859 of file tecplot_binaries.hpp.
| void slip::RegularVector2dField2d_to_plt | ( | const std::string & | file_path_name, |
| RegularVector2dField2d & | reg, | ||
| std::string | title, | ||
| std::string | zone, | ||
| std::vector< std::string > | varnames, | ||
| const int | FileType = 0 |
||
| ) |
Write a slip::RegularVector2dField2d to a binary tecplot file.
| file_path_name | String of the file path name. |
| reg | slip::RegularVector2dField2d container. |
| title | Title of the tecplot frame ("Title" by default). |
| zone | Name of the tecplot zone ("Zone" by default). |
| FileType | Type of file : 0=FULL, 1=Grid only, 2=Solution only (0 by default). |
Definition at line 2889 of file tecplot_binaries.hpp.
| void slip::RegularVector3dField3d_to_plt | ( | const std::string & | file_path_name, |
| RegularVector3dField3d & | reg, | ||
| std::string | title, | ||
| std::string | zone, | ||
| const double | SolTime, | ||
| std::vector< std::string > | varnames = std::vector<std::string>(), |
||
| const int | FileType = 0 |
||
| ) |
Write a slip::RegularVector3dField3d to a binary tecplot file.
| file_path_name | String of the file path name. |
| reg | slip::RegularVector3dField3d container. |
| title | Title of the tecplot frame ("Title" by default). |
| zone | Name of the tecplot zone ("Zone" by default). |
| SolTime | Solution Time (0 by default). |
| varnames | Vector containing the variable names ("X", "Y", "Z", "U", "V", "W" by default). |
| FileType | Type of file : 0=FULL, 1=Grid only, 2=Solution only (0 by default). |
Definition at line 1586 of file tecplot_binaries.hpp.
| void slip::RegularVector3dField3d_to_plt | ( | const std::string & | file_path_name, |
| RegularVector3dField3d & | reg, | ||
| const int | FileType = 0 |
||
| ) |
Write a slip::RegularVector3dField3d to a binary tecplot file.
| file_path_name | String of the file path name. |
| reg | slip::RegularVector3dField3d container. |
| FileType | Type of file : 0=FULL, 1=Grid only, 2=Solution only (0 by default). |
Definition at line 1879 of file tecplot_binaries.hpp.
| void slip::RegularVector3dField3d_to_plt | ( | const std::string & | file_path_name, |
| RegularVector3dField3d & | reg, | ||
| const double | SolTime, | ||
| const int | FileType = 0 |
||
| ) |
Write a slip::RegularVector3dField3d to a binary tecplot file.
| file_path_name | String of the file path name. |
| reg | slip::RegularVector3dField3d container. |
| SolTime | Solution Time. |
| FileType | Type of file : 0=FULL, 1=Grid only, 2=Solution only (0 by default). |
Definition at line 1906 of file tecplot_binaries.hpp.
| void slip::RegularVector3dField3d_to_plt | ( | const std::string & | file_path_name, |
| RegularVector3dField3d & | reg, | ||
| std::string | title, | ||
| std::string | zone, | ||
| const int | FileType = 0 |
||
| ) |
Write a slip::RegularVector3dField3d to a binary tecplot file.
| file_path_name | String of the file path name. |
| reg | slip::RegularVector3dField3d container. |
| title | Title of the tecplot frame ("Title" by default). |
| zone | Name of the tecplot zone ("Zone" by default). |
| FileType | Type of file : 0=FULL, 1=Grid only, 2=Solution only (0 by default). |
Definition at line 1934 of file tecplot_binaries.hpp.
| void slip::RegularVector3dField3d_to_plt | ( | const std::string & | file_path_name, |
| RegularVector3dField3d & | reg, | ||
| std::string | title, | ||
| std::string | zone, | ||
| std::vector< std::string > | varnames, | ||
| const int | FileType = 0 |
||
| ) |
Write a slip::RegularVector3dField3d to a binary tecplot file.
| file_path_name | String of the file path name. |
| reg | slip::RegularVector3dField3d container. |
| title | Title of the tecplot frame ("Title" by default). |
| zone | Name of the tecplot zone ("Zone" by default). |
| FileType | Type of file : 0=FULL, 1=Grid only, 2=Solution only (0 by default). |
Definition at line 1964 of file tecplot_binaries.hpp.
| void slip::reverse_container_cast | ( | Container & | cont, |
| _II & | first, | ||
| _II & | last | ||
| ) |
Get the reverse default iterators of a SLIP container.
| cont | Container. |
| first | reverse iterator to the first element of the container. |
| last | reverse iterator to one past-the-end element of the container. |
Definition at line 308 of file container_cast.hpp.
|
inline |
Apply right Givens rotation multiplication.
Perform a right multiplication of a matrix M with the Givens matrix on the col1 and col2 between the indices row1 and row2.
| M | The Container to multiply |
| col1 | The first column involved in the computation. |
| col2 | The second column involved in the computation. |
| sinus | Givens sinus. |
| cosinus | Givens cosinus. |
| row1 | the first row index. |
| row2 | the second row index. |
Definition at line 10841 of file linear_algebra.hpp.
|
inline |
right multiplies the matrix M with the Householder matrix P:
![\[ M = M(I - vv^H) \]](../../form_135.png)
| V_first | RandomAccessIterator to the beginning of the sequence (V) |
| V_last | RandomAccessIterator to one-past-the end of the sequence (V) |
| M_up | 2D iterator on the upper_left element of M. |
| M_bot | 2D iterator on the bottom_right_left element of M. |
Definition at line 11051 of file linear_algebra.hpp.
|
inline |
Computes the root mean square (rms) value of a range
![\[ \sqrt{\frac{1}{n}\sum_i x_i^2}\]](../../form_211.png)
.
| first | An InputIterator. |
| last | An InputIterator. |
Definition at line 866 of file statistics.hpp.
|
inline |
Computes the root mean square (rms) value of a range using a predicate
![\[ \sqrt{\frac{1}{n}\sum_i x_i^2}\]](../../form_211.png)
.
| first | An InputIterator. |
| last | An InputIterator. |
| pred | a predicate function |
Definition at line 3309 of file statistics.hpp.
|
inline |
Computes the root mean square (rms) value of a range over a mask
![\[ \sqrt{\frac{1}{n}\sum_i x_i^2}\]](../../form_211.png)
.
| first | An InputIterator. |
| last | An InputIterator. |
| mask_first | An InputIterator on the mask |
| value | Mask value. |
Definition at line 2185 of file statistics.hpp.
|
inline |
Computes the Givens sinus and cosinus.
| a | value |
| b | value |
| sin | Givens sinus |
| cos | Givens cosinus. |
Definition at line 10664 of file linear_algebra.hpp.
|
inline |
Computes the row norm ( 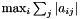 ) of a 2d range.
) of a 2d range.
| upper_left | RandomAccessIterator2d: first element of the 2d range. |
| bottom_right | RandomAccessIterator2d: one past-the-end of the 2d range. |
Definition at line 3141 of file linear_algebra.hpp.
|
inline |
Computes the row norm ( 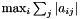 ) of a Container2d.
) of a Container2d.
| container | Container2d. |
Definition at line 3186 of file linear_algebra.hpp.
|
inline |
Computes the RQ decomposition of a matrix.
Compute the RQ decomposition of A. A = RQ where R is an upper triangular matrix and Q is an orthogonal matrix.
code is based on the QR decomposition qr_decomp
Definition at line 133 of file camera_algo.hpp.
|
inline |
Computes the same convolution of signal by a 1d-kernel.
| first | A RandomAccessIterator. |
| last | A RandomAccessIterator. |
| kernel_first | A RandomAccessIterator. |
| kernel_last | A RandomAccessIterator. |
| ksize_left | kernel size left to the "center" of the kernel |
| ksize_right | kernel size right to the "center" of the kernel |
| result | A RandomAccessIterator. slip::BORDER_TREATMENT_ZERO_PADDED by default. |
| bt | slip::BORDER_TREATMENT |
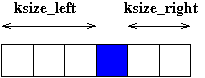
Definition at line 299 of file convolution.hpp.
|
inline |
Computes the same convolution of signal by a symmetric 1d-kernel support.
| first | A RandomAccessIterator. |
| last | A RandomAccessIterator. |
| kernel_first | A RandomAccessIterator. |
| kernel_last | A RandomAccessIterator. |
| result | A RandomAccessIterator. |
| bt | slip::BORDER_TREATMENT. slip::BORDER_TREATMENT_ZERO_PADDED by default. |
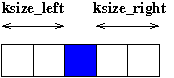
Definition at line 543 of file convolution.hpp.
|
inline |
Computes the same convolution of signal by a symmetric 1d-kernel.
| Signal | 1D Container of the input Signal. |
| Kernel | 1D Container of the kernel. |
| Result | 1D Container of the convolution result. |
| bt | slip::BORDER_TREATMENT |

Definition at line 602 of file convolution.hpp.
|
inline |
Computes the same convolution of 2d signal by a 2d-kernel.
| S_up | A RandomAccessIterator2d. |
| S_bot | A RandomAccessIterator2d. |
| kernel_up | A RandomAccessIterator2d. |
| kernel_bot | A RandomAccessIterator2d. |
| ksize_left | Number of elements left to the central point of the mask. |
| ksize_right | Number of elements right to the central point of the mask. |
| ksize_up | Number of elements up to the central point of the mask. |
| ksize_bot | Number of elements bottom to the central point of the mask |
| R_up | A RandomAccessIterator2d. |
| R_bot | A RandomAccessIterator2d. |
| bt | slip::BORDER_TREATMENT:
|
Definition at line 1372 of file convolution.hpp.
|
inline |
Computes the same convolution of 2d signal by a symmetric 2d-kernel support.
| S_up | A RandomAccessIterator2d. |
| S_bot | A RandomAccessIterator2d. |
| kernel_up | A RandomAccessIterator2d. |
| kernel_bot | A RandomAccessIterator2d. |
| R_up | A RandomAccessIterator2d. |
| R_bot | A RandomAccessIterator2d. |
| bt | slip::BORDER_TREATMENT:
|
Definition at line 2056 of file convolution.hpp.
|
inline |
Computes the same convolution of 2d signal by a symmetric 2d-kernel.
| Signal | 2D Container of the input Signal. |
| Kernel | 2D Container of the kernel. |
| Result | 2D Container of the convolution result. |
| bt | slip::BORDER_TREATMENT: |
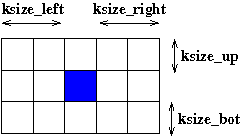
Definition at line 2120 of file convolution.hpp.
|
inline |
computes the shur decomposition of a square Matrix and copy the eigenvalues in the Eig vector:
![\[ M = Z \times H \times Z^{t}\]](../../form_158.png)
Algorithm 7.5-2 in "Matrix Computations", Golub and Van Loan.
| M | 2D container for the Input Matrix |
| H | 2D container for the H matrix |
| Z | 2D container for the Z matrix |
| Eig | container for eigenvalues |
| compute_Z | true if Z has to be computed |
| precision | defines the precision of the iterations |
Definition at line 1139 of file linear_algebra_qr.hpp.
| void slip::Schur_factorization_2by2 | ( | MatrixIterator1 | A_up, |
| MatrixIterator1 | A_bot, | ||
| MatrixIterator2 | Z_up, | ||
| MatrixIterator2 | Z_bot, | ||
| MatrixIterator3 | D_up, | ||
| MatrixIterator3 | D_bot | ||
| ) |
Computes the Schur factorization of a real 2-by-2 2d container : 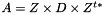
![\[ \left( \begin{array}{cc} a & b \\ c & d \end{array}\right) = \left( \begin{array}{cc} cs & -sn \\ sn & cs \end{array}\right) \times \left( \begin{array}{cc} D_{00} & D_{01} \\ D_{10} & D_{11} \end{array}\right) \times \left( \begin{array}{cc} cs & sn \\ -sn & cs \end{array}\right) \]](../../form_145.png)
where :
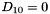 so that
so that 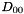 and
and 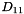 are real eigenvalues of A, or
are real eigenvalues of A, or 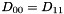 and
and 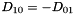 , so that
, so that 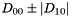 are complex conjugate eigenvalues
are complex conjugate eigenvalues | A_up | 2D iterator on the upper_left element of A container |
| A_bot | 2D iterator on the bottom_right element of A container |
| Z_up | 2D iterator on the upper_left element of Z container |
| Z_bot | 2D iterator on the bottom_right element of Z container |
| D_up | 2D iterator on the upper_left element of D container |
| D_bot | 2D iterator on the bottom_right element of D container |
Definition at line 497 of file linear_algebra_qr.hpp.
|
inline |
Computes the separable convolution of a 2d signal by two asymmetric 1d-kernels support.
| I_up | RandomAccessIterator2d on the upper_left element of the 2d signal range. |
| I_bot | RandomAccessIterator2d. on one past-the-end element of the 2d signal range. |
| k1_first | A RandomAccessIterator on the first element of the horizontal kernel. |
| k1_last | A RandomAccessIterator on one past-the-end element of the horizontal kernel. |
| ksize_left1 | kernel size left to the "center" of the horizontal kernel |
| ksize_right1 | kernel size right to the "center" of the horizontal kernel |
| bt1 | slip::BORDER_TREATMENT associated with the horizontal kernel:
|
| k2_first | A RandomAccessIterator on the first element of the vertical kernel. |
| k2_last | A RandomAccessIterator on one past-the-end element of the vertical kernel. |
| ksize_left2 | kernel size left to the "center" of the vertical kernel |
| ksize_right2 | kernel size right to the "center" of the vertical kernel |
| bt2 | slip::BORDER_TREATMENT associated with the vertical kernel:
|
| R_up | RandomAccessIterator2d on the upper_left element of the 2d convolved signal range. |
Definition at line 842 of file convolution.hpp.
|
inline |
Computes the separable convolution of a 2d signal by two symmetric 1d-kernels support.
| I_up | RandomAccessIterator2d on the upper_left element of the 2d signal range. |
| I_bot | RandomAccessIterator2d. on one past-the-end element of the 2d signal range. |
| k1_first | A RandomAccessIterator on the first element of the horizontal kernel. |
| k1_last | A RandomAccessIterator on one past-the-end element of the horizontal kernel. |
| k2_first | A RandomAccessIterator on the first element of the vertical kernel. |
| k2_last | A RandomAccessIterator on one past-the-end element of the vertical kernel. |
| R_up | RandomAccessIterator2d on the upper_left element of the 2d convolved signal range. |
| bt | slip::BORDER_TREATMENT associated with the two kernels:
|
Definition at line 931 of file convolution.hpp.
|
inline |
Computes the separable convolution of 2d signal by 2 symmetric 1d-kernel support.
| Signal | 2D Container of the input Signal |
| kernel1 | 1D Container of the horizontal kernel |
| kernel2 | 1D Container of the vertical kernel |
| Result | 2D Container of the convolution result |
| bt | slip::BORDER_TREATMENT associated with the two kernels:
|
Definition at line 995 of file convolution.hpp.
|
inline |
Computes the in-place separable convolution of a 2d signal by two asymmetric 1d-kernels support.
| I_up | RandomAccessIterator2d on the upper_left element of the 2d signal range. |
| I_bot | RandomAccessIterator2d. on one past-the-end element of the 2d signal range. |
| k1_first | A RandomAccessIterator on the first element of the horizontal kernel. |
| k1_last | A RandomAccessIterator on one past-the-end element of the horizontal kernel. |
| ksize_left1 | kernel size left to the "center" of the horizontal kernel |
| ksize_right1 | kernel size right to the "center" of the horizontal kernel |
| bt1 | slip::BORDER_TREATMENT associated with the horizontal kernel:
|
| k2_first | A RandomAccessIterator on the first element of the vertical kernel. |
| k2_last | A RandomAccessIterator on one past-the-end element of the vertical kernel. |
| ksize_left2 | kernel size left to the "center" of the vertical kernel |
| ksize_right2 | kernel size right to the "center" of the vertical kernel |
| bt2 | slip::BORDER_TREATMENT associated with the vertical kernel:
|
Definition at line 1059 of file convolution.hpp.
|
inline |
Computes the separable convolution of a 3d signal by 3 asymmetric 1d-kernels.
| I_up | RandomAccessIterator3d on the upper_left element of the 3d signal range. |
| I_bot | RandomAccessIterator3d. on one past-the-end element of the 3d signal range. |
| k1_first | A RandomAccessIterator on the first element of the horizontal kernel. |
| k1_last | A RandomAccessIterator on one past-the-end element of the horizontal kernel. |
| ksize_left1 | kernel size left to the "center" of the horizontal kernel |
| ksize_right1 | kernel size right to the "center" of the horizontal kernel |
| bt1 | slip::BORDER_TREATMENT associated with the horizontal kernel:
|
| k2_first | A RandomAccessIterator on the first element of the vertical kernel. |
| k2_last | A RandomAccessIterator on one past-the-end element of the vertical kernel. |
| ksize_left2 | kernel size left to the "center" of the vertical kernel |
| ksize_right2 | kernel size right to the "center" of the vertical kernel |
| bt2 | slip::BORDER_TREATMENT associated with the vertical kernel:
|
| k3_first | A RandomAccessIterator on the first element of the depth kernel. |
| k3_last | A RandomAccessIterator on one past-the-end element of the depth kernel. |
| ksize_left3 | kernel size left to the "center" of the depth kernel |
| ksize_right3 | kernel size right to the "center" of the depth kernel |
| bt3 | slip::BORDER_TREATMENT associated with the depth kernel:
|
| R_up | RandomAccessIterator3d on the upper_left element of the 3d convolved signal range. |
Definition at line 2596 of file convolution.hpp.
|
inline |
Computes the separable convolution of a 3d signal by 3 symmetric 1d-kernels.
| I_up | RandomAccessIterator3d on the upper_left element of the 3d signal range. |
| I_bot | RandomAccessIterator3d. on one past-the-end element of the 3d signal range. |
| k1_first | A RandomAccessIterator on the first element of the horizontal kernel. |
| k1_last | A RandomAccessIterator on one past-the-end element of the horizontal kernel. |
| k2_first | A RandomAccessIterator on the first element of the vertical kernel. |
| k2_last | A RandomAccessIterator on one past-the-end element of the vertical kernel. |
| k3_first | A RandomAccessIterator on the first element of the depth kernel. |
| k3_last | A RandomAccessIterator on one past-the-end element of the depth kernel. |
| R_up | RandomAccessIterator3d on the upper_left element of the 3d convolved signal range. |
| bt | slip::BORDER_TREATMENT associated with the kernels:
|
Definition at line 2728 of file convolution.hpp.
|
inline |
Computes the separable convolution of 3d signal by a 3 1d-kernel.
| Signal | 3D Container of the input Signal. |
| kernel1 | 1D Container of the horizontal kernel. |
| kernel2 | 1D Container of the vertical kernel. |
| kernel3 | 1D Container of the depth kernel. |
| Result | 3D Container of the convolution result. |
| bt | slip::BORDER_TREATMENT associated with the kernels:
|
Definition at line 2808 of file convolution.hpp.
|
inline |
Computes the in-place separable convolution of a 3d signal by 3 asymmetric 1d-kernels.
| I_up | RandomAccessIterator3d on the upper_left element of the 3d signal range. |
| I_bot | RandomAccessIterator3d. on one past-the-end element of the 3d signal range. |
| k1_first | A RandomAccessIterator on the first element of the horizontal kernel. |
| k1_last | A RandomAccessIterator on one past-the-end element of the horizontal kernel. |
| ksize_left1 | kernel size left to the "center" of the horizontal kernel |
| ksize_right1 | kernel size right to the "center" of the horizontal kernel |
| bt1 | slip::BORDER_TREATMENT associated with the horizontal kernel:
|
| k2_first | A RandomAccessIterator on the first element of the vertical kernel. |
| k2_last | A RandomAccessIterator on one past-the-end element of the vertical kernel. |
| ksize_left2 | kernel size left to the "center" of the vertical kernel |
| ksize_right2 | kernel size right to the "center" of the vertical kernel |
| bt2 | slip::BORDER_TREATMENT associated with the vertical kernel:
|
| k3_first | A RandomAccessIterator on the first element of the depth kernel. |
| k3_last | A RandomAccessIterator on one past-the-end element of the depth kernel. |
| ksize_left3 | kernel size left to the "center" of the depth kernel |
| ksize_right3 | kernel size right to the "center" of the depth kernel |
| bt3 | slip::BORDER_TREATMENT associated with the depth kernel:
|
Definition at line 2887 of file convolution.hpp.
|
inline |
Computes the separable 2d convolution of signal using the fft algorithm.
| I_up | RandomAccessIterator2d on the upper_left element of the 2d signal range. |
| I_bot | RandomAccessIterator2d. on one past-the-end element of the 2d signal range. |
| k1_first | A RandomAccessIterator on the first element of the horizontal kernel. |
| k1_last | A RandomAccessIterator on one past-the-end element of the horizontal kernel. |
| k2_first | A RandomAccessIterator on the first element of the vertical kernel. |
| k2_last | A RandomAccessIterator on one past-the-end element of the vertical kernel. |
| R_up | RandomAccessIterator2d on the upper_left element of the 2d convolved signal range. |
Definition at line 1142 of file convolution.hpp.
|
inline |
Computes the fft convolution of a 2d signal.
| Signal | 2D Container of the input Signal |
| kernel1 | 1D Container of the horizontal kernel |
| kernel2 | 1D Container of the vertical kernel |
| Result | 2D Container of the convolution result |
Definition at line 1206 of file convolution.hpp.
|
inline |
Computes the separable 3d convolution of signal using the fft algorithm.
| I_up | RandomAccessIterator3d on the upper_left element of the 3d signal range. |
| I_bot | RandomAccessIterator3d. on one past-the-end element of the 3d signal range. |
| k1_first | A RandomAccessIterator on the first element of the horizontal kernel. |
| k1_last | A RandomAccessIterator on one past-the-end element of the horizontal kernel. |
| k2_first | A RandomAccessIterator on the first element of the vertical kernel. |
| k2_last | A RandomAccessIterator on one past-the-end element of the vertical kernel. |
| k3_first | A RandomAccessIterator on the first element of the depth kernel. |
| k3_last | A RandomAccessIterator on one past-the-end element of the depth kernel. |
| R_up | RandomAccessIterator3d on the upper_left element of the 3d convolved signal range. |
Definition at line 3013 of file convolution.hpp.
|
inline |
Computes the separable fft convolution of 3d signal by 3 1d-kernel.
| Signal | 3D Container of the input Signal. |
| kernel1 | 1D Container of the horizontal kernel. |
| kernel2 | 1D Container of the vertical kernel. |
| kernel3 | 1D Container of the depth kernel. |
| Result | 3D Container of the convolution result. |
Definition at line 3120 of file convolution.hpp.
| void slip::set_diagonal | ( | RandomAccessIterator1 | diag_first, |
| RandomAccessIterator1 | diag_last, | ||
| Container2d & | container, | ||
| const int | diag_number = 0 |
||
| ) |
Set the diagonal [diag_first,diag_last) in the diagonal diag_number of a 2d container.
| diag_first | RandomAccessIterator to the first element of the diagonal. |
| diag_last | RandomAccessIterator to one past-the-end element of the diagonal. |
| container | A 2d container |
| diag_number | number of the diagonal:
|
Definition at line 3442 of file linear_algebra.hpp.
| void slip::shift | ( | Real & | p, |
| Real & | r, | ||
| Real & | q, | ||
| Real & | sigma | ||
| ) |
Given a matrix
![\[ M = \left( \begin{array}{cc} p&r\\ 0&q\\ \end{array} \right) \]](../../form_160.png)
compute the smallest singular value of this matrix.
| p | element of the matrix M |
| r | element of the matrix M. |
| q | element of the matrix M. |
| sigma | smallest singular value of this matrix. |
Definition at line 418 of file linear_algebra_svd.hpp.
|
inline |
Computes the sign of a.
| a | of generic type T |
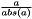 if a != 0; T(1) if a == 0.
if a != 0; T(1) if a == 0. Definition at line 233 of file macros.hpp.
|
related |
Definition at line 1491 of file KVector.hpp.
|
related |
Definition at line 2066 of file Vector.hpp.
|
related |
Definition at line 2079 of file Signal.hpp.
|
related |
Definition at line 3945 of file Matrix.hpp.
|
related |
Definition at line 5101 of file HyperVolume.hpp.
|
related |
Definition at line 5110 of file Matrix4d.hpp.
|
related |
Definition at line 5751 of file Matrix3d.hpp.
|
related |
Definition at line 6068 of file Volume.hpp.
|
related |
Definition at line 1593 of file KVector.hpp.
|
related |
Definition at line 2161 of file Vector.hpp.
|
related |
Definition at line 2174 of file Signal.hpp.
|
related |
Definition at line 4040 of file Matrix.hpp.
|
related |
Definition at line 5164 of file HyperVolume.hpp.
|
related |
Definition at line 5173 of file Matrix4d.hpp.
|
related |
Definition at line 5814 of file Matrix3d.hpp.
|
related |
Definition at line 6131 of file Volume.hpp.
|
inline |
Computes the skewness of a range
![\[\frac{\frac{1}{n}\sum_i (x_i-\overline{x})^3}{\left(\sqrt{\frac{1}{n}\sum_i (x_i-\overline{x})^2}\right)^3}\]](../../form_209.png)
skewness is a measure of the asymmetry of the probability distribution of a real-valued random variable.
| first | An InputIterator. |
| last | An InputIterator. |
| std_dev | The standard deviation of the container itself. |
Definition at line 770 of file statistics.hpp.
|
inline |
Computes the skewness of a range using a predicate
![\[\frac{\frac{1}{n}\sum_i (x_i-\overline{x})^3}{\left(\sqrt{\frac{1}{n}\sum_i (x_i-\overline{x})^2}\right)^3}\]](../../form_209.png)
skewness is a measure of the asymmetry of the probability distribution of a real-valued random variable.
| first | An InputIterator. |
| last | An InputIterator. |
| mean | The mean of the range itself using the predicate. |
| pred | a predicate function |
Definition at line 3188 of file statistics.hpp.
|
inline |
Computes the skewness of a range over a mask
![\[\frac{\frac{1}{n}\sum_i (x_i-\overline{x})^3}{\left(\sqrt{\frac{1}{n}\sum_i (x_i-\overline{x})^2}\right)^3}\]](../../form_209.png)
skewness is a measure of the asymmetry of the probability distribution of a real-valued random variable.
| first | An InputIterator. |
| last | An InputIterator. |
| mask_first | An InputIterator on the mask |
| mean | The mean of the range itself over the mask. |
| value | Mask value. |
Definition at line 2047 of file statistics.hpp.
|
inline |
Computes the signal to noise ration (snr) of two ranges : 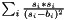 .
.
| first1 | An InputIterator to the first element of the signal. |
| last1 | An InputIterator to the one past-the-end element of the signal. |
| first2 | An InputIterator to the "noise" range. |
Definition at line 799 of file compare.hpp.
|
inline |
Computes the decibel signal to noise ration (snr) of two ranges : 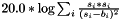 .
.
| first1 | An InputIterator to the first element of the signal. |
| last1 | An InputIterator to the one past-the-end element of the signal. |
| first2 | An InputIterator to the "noise" range. |
Definition at line 948 of file compare.hpp.
| Real slip::snr_dB_if | ( | InputIterator1 | first1, |
| InputIterator1 | last1, | ||
| InputIterator2 | first2, | ||
| Predicate | pred | ||
| ) |
Computes the decibel signal to noise ration (snr) of two ranges according to a predicate: 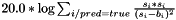 .
.
| first1 | An InputIterator. |
| last1 | An InputIterator. |
| first2 | An InputIterator. |
| pred | A predicate. |
Definition at line 1027 of file compare.hpp.
|
inline |
Computes the decibel signal to noise ration (snr) of two ranges according to a mask sequence : 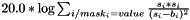 .
.
| first1 | An InputIterator. |
| last1 | An InputIterator. |
| mask_first | An input iterator. |
| first2 | An InputIterator. |
| value | true value of the mask range. Default is 1. |
Definition at line 984 of file compare.hpp.
| Real slip::snr_if | ( | InputIterator1 | first1, |
| InputIterator1 | last1, | ||
| InputIterator2 | first2, | ||
| Predicate | pred | ||
| ) |
Computes the signal to noise ration (snr) of two ranges according to a Predicate.
| first1 | An input iterator. |
| last1 | An input iterator. |
| first2 | An input iterator. |
| pred | A predicate. |
Definition at line 903 of file compare.hpp.
|
inline |
Computes the signal to noise ration (snr) of two ranges according to a mask sequence : 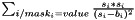 .
.
| first1 | An InputIterator. |
| last1 | An InputIterator. |
| mask_first | An input iterator. |
| first2 | An InputIterator. |
| value | true value of the mask range. Default is 1. |
Definition at line 845 of file compare.hpp.
|
inline |
Spectral radius of a matrix 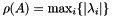 .
.
| A | Matrix container |
Definition at line 268 of file linear_algebra_eigen.hpp.
|
inline |
Split a file_name in two substrings: the file_path_name string without the extension and the extension string.
| file_path_name | String of the file path name |
| file_path_name_cut | String of the file path name cut |
| ext | extension string. |
Definition at line 159 of file io_tools.hpp.
|
inline |
Computes the split radix Discrete Cosinus Transform II of a container (from FFTPACK.hpp).
| in_begin | A BidirectionalIterator to iterate from the beginning of the input data |
| in_end | A BidirectionalIterator to iterate from the end of the input data |
| out_begin | A BidirectionalIterator to iterate from the beginning of the output data) |
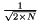
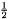 was done in order to obtain the same results than the fftw_dct function
was done in order to obtain the same results than the fftw_dct function
|
inline |
Computes the split radix Discrete Cosinus Transform III (i.e. idct) of a container (from FFTPACK.hpp).
| in_begin | A BidirectionalIterator to iterate from the beginning of the input data |
| in_end | A BidirectionalIterator to iterate from the end of the input data |
| out_begin | A BidirectionalIterator to iterate from the beginning of the output data |
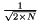
|
inline |
Computes the split radix fft backward of a container (from FFTPACK.hpp).
| in_begin | A BidirectionalIterator to iterate from the beginning of the input data |
| in_end | A BidirectionalIterator to iterate from the end of the input data |
| out_begin | A BidirectionalIterator to iterate from the beginning of the output data |
|
inline |
Computes the split-radix ifft2d of a container with 2d iterators.
| in_upper_left | |
| in_bottom_right | |
| out_upper_left |
|
inline |
Computes the split-radix ifft2d of a container.
| datain | The input datas |
| dataout | The output datas |
|
inline |
Computes the split-radix ifft3d of a container with 3d iterators.
| in_front_upper_left | |
| in_back_bottom_right | |
| out_front_upper_left |
|
inline |
Computes the split-radix ifft3d of a container 3d.
| datain | The input datas |
| dataout | The output datas |
|
inline |
Computes the split-radix ifft4d of a container with 4d iterators.
| in_first_front_upper_left | |
| in_last_back_bottom_right | |
| out_first_front_upper_left |
|
inline |
Computes the split-radix ifft4d of a container 4d.
| datain | The input datas |
| dataout | The output datas |
|
related |
Definition at line 1445 of file KVector.hpp.
|
related |
Definition at line 2023 of file Vector.hpp.
|
related |
Definition at line 2036 of file Signal.hpp.
|
related |
Definition at line 3902 of file Matrix.hpp.
|
related |
Definition at line 5074 of file HyperVolume.hpp.
|
related |
Definition at line 5083 of file Matrix4d.hpp.
|
related |
Definition at line 5724 of file Matrix3d.hpp.
|
related |
Definition at line 6041 of file Volume.hpp.
|
inline |
Computes the Structural SIMilarity (SSIM) beetween two data ranges
![\[ SSIM(x,y) = \frac{(2\mu_x\mu_y + c_1)(2cov_{xy}+c_2)}{(\mu_x^2+\mu_y^2+c_1)(\sigma_x^2+\sigma_y^2+c_2)} \]](../../form_29.png)
where.
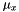 is the mean of x
is the mean of x 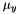 is the mean of y
is the mean of y 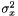 is the variance of x
is the variance of x 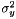 is the variance of y
is the variance of y 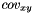 is the covariance of x and y
is the covariance of x and y 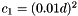 ,
, 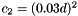 two variable to avoid division by 0
two variable to avoid division by 0 | first1 | An InputIterator. |
| last1 | An InputIterator. |
| first2 | An InputIterator. |
| d | pixel dynamic (255 by default). |
Definition at line 2222 of file compare.hpp.
|
inline |
Computes the Sructural SIMilarity (SSIM) beetween two data ranges according to a predicate
![\[ SSIM(x,y) = \frac{(2\mu_x\mu_y + c_1)(2cov_{xy}+c_2)}{(\mu_x^2+\mu_y^2+c_1)(\sigma_x^2+\sigma_y^2+c_2)} \]](../../form_29.png)
where.
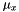 is the mean of x
is the mean of x 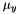 is the mean of y
is the mean of y 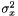 is the variance of x
is the variance of x 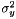 is the variance of y
is the variance of y 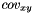 is the covariance of x and y
is the covariance of x and y 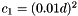 ,
, 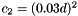 two variable to avoid division by 0
two variable to avoid division by 0 | first1 | An InputIterator. |
| last1 | An InputIterator. |
| first2 | An InputIterator. |
| pred | A predicate. |
| d | pixel dynamic (255 by default) |
Definition at line 2367 of file compare.hpp.
|
inline |
Computes the structural similarity beetween two data ranges according to a mask range
![\[ SSIM(x,y) = \frac{(2\mu_x\mu_y + c_1)(2cov_{xy}+c_2)}{(\mu_x^2+\mu_y^2+c_1)(\sigma_x^2+\sigma_y^2+c_2)} \]](../../form_29.png)
where.
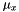 is the mean of x
is the mean of x 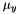 is the mean of y
is the mean of y 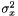 is the variance of x
is the variance of x 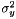 is the variance of y
is the variance of y 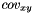 is the covariance of x and y
is the covariance of x and y 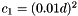 ,
, 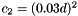 two variable to avoid division by 0
two variable to avoid division by 0 | first1 | An InputIterator. |
| last1 | An InputIterator. |
| maskFirst | A MaskIterator |
| first2 | An InputIterator. |
| value | A value corresponding to the mask |
| d | pixel dynamic (255 by default) |
Definition at line 2288 of file compare.hpp.
| void slip::statistics | ( | InputIterator | first, |
| InputIterator | last, | ||
| slip::Statistics< T > & | statistic | ||
| ) |
compute all statistics of a range
| first | An InputIterator. |
| last | An InputIterator. |
| statistic | slip::statistics |
Definition at line 3665 of file statistics.hpp.
| void slip::statistics_if | ( | InputIterator | first, |
| InputIterator | last, | ||
| slip::Statistics< T > & | statistic, | ||
| Predicate | pred | ||
| ) |
compute all statistics of a range according to a preidcate.
| first | An InputIterator. |
| last | An InputIterator. |
| statistic | slip::statistics |
| pred | a predicate function. |
Definition at line 3954 of file statistics.hpp.
| void slip::statistics_mask | ( | InputIterator | first, |
| InputIterator | last, | ||
| MaskIterator | mask_first, | ||
| slip::Statistics< T > & | statistic, | ||
| typename std::iterator_traits< MaskIterator >::value_type | value = typename std::iterator_traits<MaskIterator>::value_type(1) |
||
| ) |
compute all statistics of a range according to a mask range.
| first | An InputIterator. |
| last | An InputIterator. |
| mask_first | An InputIterator of the mask |
| statistic | slip::Statistics which contains all the statistics of the range. |
| value | Mask value. |
Definition at line 3791 of file statistics.hpp.
|
inline |
Computes the standard crosscorrelation between two sequences: 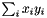 . Multiplies successive elements from the two ranges and adds each product into the accumulated value using operator+(). The values in the ranges are processed in order.
. Multiplies successive elements from the two ranges and adds each product into the accumulated value using operator+(). The values in the ranges are processed in order.
| first | An InputIterator. |
| last | An InputIterator. |
| first2 | An InputIterator. |
Definition at line 180 of file correlation.hpp.
|
inline |
Computes the standard crosscorrelation between two Images.
| in1_upper_left | : A 2d input iterator (image). |
| in1_bottom_right | : A 2d input iterator (image). |
| in2_upper_left | : A 2d input iterator (mask). |
| in2_bottom_right | : A 2d input iterator (mask). |
| out_upper_left | : A 2d output iterator (result). |
| out_bottom_right | : A 2d output iterator (result). |
Definition at line 2117 of file correlation.hpp.
| T slip::std_crosscorrelation_if | ( | InputIterator1 | first1, |
| InputIterator1 | last1, | ||
| InputIterator2 | first2, | ||
| Predicate | pred | ||
| ) |
Computes the standard crosscorrelation between two sequences according to a Predicate. 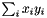 .
.
| first1 | An InputIterator. |
| last1 | An InputIterator. |
| first2 | An InputIterator. |
| pred | A predicate. |
Definition at line 278 of file correlation.hpp.
|
inline |
Computes the standard crosscorrelation between two sequences according to a mask sequence 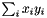 . Multiplies successive elements accordind to a mask sequence from the two ranges and adds each product into the accumulated value using operator+(). The values in the ranges are processed in order.
. Multiplies successive elements accordind to a mask sequence from the two ranges and adds each product into the accumulated value using operator+(). The values in the ranges are processed in order.
| first1 | An InputIterator. |
| last1 | An InputIterator. |
| mask_first | An input iterator. |
| first2 | An InputIterator. |
| value | true value of the mask range. Default is 1. |
Definition at line 223 of file correlation.hpp.
|
inline |
Computes the standard deviation of a range
![\[\sqrt{\frac{1}{n}\sum_i (x_i-\overline{x})^2}\]](../../form_205.png)
.
| first | An InputIterator. |
| last | An InputIterator. |
| mean | The mean of the container itself. |
Definition at line 596 of file statistics.hpp.
|
inline |
Computes the standard deviation of a range using a predicate
![\[\sqrt{\frac{1}{n}\sum_i (x_i-\overline{x})^2}\]](../../form_205.png)
.
| first | An InputIterator. |
| last | An InputIterator. |
| mean | The mean of the range itself using the predicate. |
| pred | a predicate function |
Definition at line 2969 of file statistics.hpp.
|
inline |
Computes the standard deviation of a range over a mask
![\[\sqrt{\frac{1}{n}\sum_i (x_i-\overline{x})^2}\]](../../form_205.png)
.
| first | An InputIterator. |
| last | An InputIterator. |
| mask_first | An InputIterator on the mask |
| mean | The mean of the range itself over the mask. |
| value | Mask value. |
Definition at line 1812 of file statistics.hpp.
| void slip::studentize | ( | RandomAccessIterator | first, |
| RandomAccessIterator | last, | ||
| RandomAccessIterator2 | out_first | ||
| ) |
Substracts its mean to a range and divide it by its standard deviation.
| first | RandomAccessIterator to the first element of the range. |
| last | RandomAccessIterator to one past-the-end element of the range. |
| out_first | RandomAccessIterator to the first element of the range. |
Definition at line 1418 of file statistics.hpp.
|
inline |
Substracts its mean to a range and divide it by its standard deviation using a predicate.
| first | An InputIterator. |
| last | An InputIterator |
| pred | a predicate function |
| out_first | An OutputIterator |
Definition at line 3600 of file statistics.hpp.
|
inline |
Substracts its mean to a range and divide it by its standard deviation according a mask.
| first | An InputIterator. |
| last | An InputIterator |
| mask_first | An InputIterator on the mask |
| out_first | An OuputIterator. |
| value | Mask value. |
Definition at line 2540 of file statistics.hpp.
|
inline |
find the smaller non null (according to the precision) subdiagonal element of a matrix
| A_up | 2D iterator on the upper_left element of A container |
| A_bot | 2D iterator on the bottom_right element of A container |
| precision | of the zero |
Definition at line 419 of file linear_algebra_qr.hpp.
| void slip::svd | ( | const Matrix1 & | M, |
| Matrix2 & | U, | ||
| RandomAccessIterator | S_first, | ||
| RandomAccessIterator | S_last, | ||
| Matrix3 & | V, | ||
| const int | max_it = 75 |
||
| ) |
(thin) Singular Value Decomposition Given a matrix M, this function computes its singular value decomposition, Any n*p matrix M whose number of rows n is greater than or equal to its number of columns p, can be written as the product of an n*p column-orthogonal matrix Up, an p*p diagonal matrix S with positive or zero elements (the singular values), and the hermitian transpose of an p*p orthogonal matrix V
![\[ M = \left( \begin{array}{ccc} u_{1,1}&\cdots&u_{1,p}\\ \vdots&&\vdots\\ u_{n,1}&\cdots&u_{n,p}\\ \end{array} \right) \left( \begin{array}{cccc} s_{1,1}&0&\cdots&0\\ 0&\ddots&\ddots&\vdots\\ \vdots&\ddots&\ddots&0\\ 0&\cdots&0&s_{p,p}\\ \end{array} \right) \left( \begin{array}{ccc} v_{1,1}&\cdots&v_{1,p}\\ \vdots&&\vdots\\ v_{p,1}&\cdots&v_{p,p}\\ \end{array} \right)^H \]](../../form_161.png)
| M | n*p matrix |
| U | n*p orthogonal matrix |
| S_first | diagonal of the Singular matrix with positive or zero elements |
| S_last | diagonal of the Singular matrix with positive or zero elements |
| V | p*p orthogonal matrix (not its transpose) |
| max_it | maximum number of iterations. |
Definition at line 591 of file linear_algebra_svd.hpp.
| void slip::svd | ( | const Matrix & | X, |
| Matrix & | U, | ||
| Matrix2 & | S, | ||
| Matrix & | V, | ||
| const int | max_it = 75 |
||
| ) |
(thin) Singular Value Decomposition Given a matrix M, this function computes its singular value decomposition, Any n*p matrix M whose number of rows n is greater than or equal to its number of columns p, can be written as the product of an n*p column-orthogonal matrix Up, an p*p diagonal matrix S with positive or zero elements (the singular values), and the transpose of an p*p orthogonal matrix V
![\[ M = \left( \begin{array}{ccc} u_{1,1}&\cdots&u_{1,p}\\ \vdots&&\vdots\\ u_{n,1}&\cdots&u_{n,p}\\ \end{array} \right) \left( \begin{array}{cccc} s_{1,1}&0&\cdots&0\\ 0&\ddots&\ddots&\vdots\\ \vdots&\ddots&\ddots&0\\ 0&\cdots&0&s_{p,p}\\ \end{array} \right) \left( \begin{array}{ccc} v_{1,1}&\cdots&v_{1,p}\\ \vdots&&\vdots\\ v_{p,1}&\cdots&v_{p,p}\\ \end{array} \right)^H \]](../../form_161.png)
| X | n*p matrix |
| U | n*p orthogonal matrix |
| S | p*p diagonal matrix with positive or zero elements |
| V | p*p orthogonal matrix (not its transpose) |
| max_it | maximum number of iterations. |
Definition at line 774 of file linear_algebra_svd.hpp.
|
inline |
Singular Value Approximation of a matrix from its Singular Value Decomposition given by U, W and V: 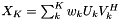 .
.
| U | matrix container |
| S_first | RandomAccessIterator to the first element of the singular values vector |
| S_last | RandomAccessIterator to one-past-the-end element of the singular values vector |
| V | matrix container |
| K | length of the approximation |
| X | matrix container |
Definition at line 836 of file linear_algebra_svd.hpp.
|
inline |
Singular Value Approximation of a matrix from its Singular Value Decomposition given by U, W and V: 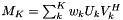 .
.
| U | matrix container |
| W | Matrix container |
| V | matrix container |
| K | length of the approximation |
| M | matrix container |
Definition at line 904 of file linear_algebra_svd.hpp.
|
inline |
Singular Value inverse of a matrix from its Singular Value Decomposition given by U, W and V.
| U | matrix container |
| W_first | RandomAccessIterator to the first element of the singular values vector |
| W_last | RandomAccessIterator to one-past-the-end element of the singular values vector |
| V | matrix |
| Ainv | Invert matrix. |
Definition at line 1148 of file linear_algebra_svd.hpp.
|
inline |
Singular Value inverse of a matrix.
| A | matrix to invert. |
| Ainv | inverted matrix. |
Definition at line 1221 of file linear_algebra_svd.hpp.
|
inline |
Linear Least Square fitting using SVD.
Given a set of data points x =(x1,...,xN), y = (y1,..yN) with individual standard deviations s = (s1,..sN) use chi2 minimization to determine the coefficients p = (p1,...,pM) of the fitting function y = sum_j pj Fj(x). Here we solve the fitting equations using singular value decomposition (SVD) of the NxM matrix A such that aij = Fj(xi)/si. The program returns values for the fit parameters [p_first,p_last) and chi2. The user supplies a functor EvalBasis that return a basis function evaluated at x (Fj(xi)).
| x_first | RandomAccessIterator to the x datas |
| x_last | RandomAccessIterator to the x datas |
| y_first | RandomAccessIterator to the y datas |
| s_first | RandomAccessIterator to the sigma datas |
| p_first | RandomAccessIterator to the estimated parameters |
| p_last | RandomAccessIterator to the estimated parameters |
| basis_fun | functor to the function which gives the values obtained by the basis functions Fj. For example, slip::EvalPowerBasis gives (1,x,x^2,...,x^M) and is adapted to a polynomial fitting |
Definition at line 155 of file linear_least_squares.hpp.
|
inline |
Linear Least Square fitting using SVD.
Given a set of data points x =(x1,...,xN), y = (y1,..yN) with individual standard deviations s = (s1,..sN) use chi2 minimization to determine the coefficients p = (p1,...,pM) of the fitting function y = sum_j pj Fj(x). Here we solve the fitting equations using singular value decomposition (SVD) of the NxM matrix A such that aij = Fj(xi)/si. The program returns values for the fit parameters [p_first,p_last) and chi2. The user supplies a functor EvalBasis that return a basis function evaluated at x (Fj(xi)).
| X | Vector which contains the x datas. |
| Y | Vector which contains the y datas. |
| S | Vector which contains the standard deviation of the datas. |
| P | Vector which contains the parameters datas. |
| basis_fun | functor to the function which gives the values obtained by the basis functions Fj. For example, slip::EvalPowerBasis gives (1,x,x^2,...,x^M) and is adapted to a polynomial fitting |
Definition at line 269 of file linear_least_squares.hpp.
|
inline |
Linear Least Square fitting using SVD.
Given a set of data points x =(x1,...,xN), y = (y1,..yN) use chi2 minimization to determine the coefficients p = (p1,...,pM) of the fitting function y = sum_j pj Fj(x). Here we solve the fitting equations using singular value decomposition (SVD) of the NxM matrix A such that aij = Fj(xi)/si. The program returns values for the fit parameters [p_first,p_last) and chi2. The user supplies a functor EvalBasis that return a basis function evaluated at x (Fj(xi)).
| x_first | RandomAccessIterator to the x datas |
| x_last | RandomAccessIterator to the x datas |
| y_first | RandomAccessIterator to the y datas |
| p_first | RandomAccessIterator to the estimated parameters |
| p_last | RandomAccessIterator to the estimated parameters |
| basis_fun | functor to the function which gives the values obtained by the basis functions Fj. For example, slip::EvalPowerBasis gives (1,x,x^2,...,x^M) and is adapted to a polynomial fitting |
Definition at line 343 of file linear_least_squares.hpp.
|
inline |
Linear Least Square fitting using SVD.
Given a set of data points x =(x1,...,xN), y = (y1,..yN) use chi2 minimization to determine the coefficients p = (p1,...,pM) of the fitting function y = sum_j pj Fj(x). Here we solve the fitting equations using singular value decomposition (SVD) of the NxM matrix A such that aij = Fj(xi)/si. The program returns values for the fit parameters [p_first,p_last) and chi2. The user supplies a functor EvalBasis that return a basis function evaluated at x (Fj(xi)).
| X | Vector which contains the x datas. |
| Y | Vector which contains the y datas. |
| P | Vector which contains the parameters datas. |
| basis_fun | functor to the function which gives the values obtained by the basis functions Fj. For example, slip::EvalPowerBasis gives (1,x,x^2,...,x^M) and is adapted to a polynomial fitting |
Definition at line 443 of file linear_least_squares.hpp.
|
inline |
nd Linear Least Square fitting using SVD.
Given a set of data points X =(X1,...,XN) of dimension N, y = (y1,..yN) with individual standard deviations s = (s1,..sN) use chi2 minimization to determine the coefficients p = (p1,...,pM) of the fitting function y = sum_j pj Fj(X). Here we solve the fitting equations using singular value decomposition (SVD) of the NxM matrix A such that aij = Fj(Xi)/si. The program returns values for the fit parameters [p_first,p_last) and chi2. The user supplies a functor EvalBasis that return a basis function evaluated at x (Fj(Xi)).
| x_first | RandomAccessIterator to the x datas |
| x_last | RandomAccessIterator to the x datas |
| y_first | RandomAccessIterator to the y datas |
| s_first | RandomAccessIterator to the sigma datas |
| p_first | RandomAccessIterator to the estimated parameters |
| p_last | RandomAccessIterator to the estimated parameters |
| order | Order of the process. |
| basis_fun | functor to the function which gives the values obtained by the basis functions Fj. For example, slip::EvalPower2dBasis gives (1,x1,x1^2,x2,x1x2,x2^2...) and is adapted to a 2d-polynomial fitting |
Definition at line 549 of file linear_least_squares.hpp.
|
inline |
nd Linear Least Square fitting using SVD.
Given a set of N points of dimension dim X =(X1,...,XN), y = (y1,..yN) use chi2 minimization to determine the coefficients p = (p1,...,pM) of the fitting function y = sum_j pj Fj(X). Here we solve the fitting equations using singular value decomposition (SVD) of the NxM matrix A such that aij = Fj(Xi). The program returns values for the fit parameters [p_first,p_last) and chi2. The user supplies a functor EvalBasis that return a basis function evaluated at X (Fj(Xi)).
| x_first | RandomAccessIterator to the x datas |
| x_last | RandomAccessIterator to the x datas |
| y_first | RandomAccessIterator to the y datas |
| p_first | RandomAccessIterator to the estimated parameters |
| p_last | RandomAccessIterator to the estimated parameters |
| order | Order of the process. |
| basis_fun | functor to the function which gives the values obtained by the basis functions Fj. For example, slip::EvalPower2dBasis gives (1,x1,x1^2,x2,x1x2,x2^2...) and is adapted to a 2d-polynomial fitting |
Definition at line 697 of file linear_least_squares.hpp.
|
inline |
nd Linear Least Square fitting using SVD.
Given a set of data points of N dimension X =(X1,...,XN), y = (y1,..yN) use chi2 minimization to determine the coefficients p = (p1,...,pM) of the fitting function y = sum_j pj Fj(X). Here we solve the fitting equations using singular value decomposition (SVD) of the NxM matrix A such that aij = Fj(Xi). The program returns values for the fit parameters [p_first,p_last) and chi2. The user supplies a functor EvalBasis that return a basis function evaluated at X (Fj(Xi)).
| X | Vector which contains the x datas. |
| Y | Vector which contains the y datas. |
| P | Vector which contains the parameters datas. |
| order | Order of the approximation. |
| basis_fun | functor to the function which gives the values obtained by the basis functions Fj. For example, slip::EvalPower2dBasis gives (1,x1,x1^2,x2,x1x2,x2^2...) and is adapted to a 2d polynomial fitting |
Definition at line 826 of file linear_least_squares.hpp.
|
inline |
Solve Linear (USV^H).X = B where U, S and V are provided by a svd decomposition.
| U | matrix U. |
| W_first | RandomAccesIterator to the first element of the singular values vector |
| W_last | RandomAccesIterator to one-past-the-end element of singular values vector |
| V | matrix V. |
| B_first | RandomAccesIterator to the first element of the vector to match |
| B_last | RandomAccesIterator to one-past-the-end element of the vector to match |
| X_first | RandomAccesIterator to the first element of the Result vector |
| X_last | RandomAccesIterator to one-past-the-end element of the Result vector |
Definition at line 950 of file linear_algebra_svd.hpp.
|
inline |
Solve Linear Equation A.X = B using SVD decomposition.
| A | matrix A. |
| X_first | RandomAccesIterator to the first element of the Result vector |
| X_last | RandomAccesIterator to one-past-the-end element of the Result vector |
| B_first | RandomAccesIterator to the first element of the vector to match |
| B_last | RandomAccesIterator to one-past-the-end element of the vector to match |
Definition at line 1035 of file linear_algebra_svd.hpp.
|
inline |
Solve Linear Equation A.X = B using SVD decomposition.
| A | matrix A. |
| X | Result vector |
| B | vector to match |
Definition at line 1114 of file linear_algebra_svd.hpp.
|
inline |
Solve the sylvester equation (from Z.Bai and J.W. Demmel article : -On Swapping Diagonal Blocks in Real Schur Form- In Linear Algebra and its Applications 186:73-95(1993)) : 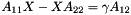 .
.
| S | the Schur matrix |
| b11 | the A11 box2d |
| b22 | the A22 box2d |
| g | gamma factor |
| X | the resulting matrix |
Definition at line 1169 of file linear_algebra_qr.hpp.
|
related |
Definition at line 1528 of file KVector.hpp.
|
related |
Definition at line 2101 of file Vector.hpp.
|
related |
Definition at line 2114 of file Signal.hpp.
|
related |
Definition at line 3979 of file Matrix.hpp.
|
related |
Definition at line 5119 of file HyperVolume.hpp.
|
related |
Definition at line 5128 of file Matrix4d.hpp.
|
related |
Definition at line 5769 of file Matrix3d.hpp.
|
related |
Definition at line 6086 of file Volume.hpp.
|
related |
Definition at line 1602 of file KVector.hpp.
|
related |
Definition at line 2170 of file Vector.hpp.
|
related |
Definition at line 2183 of file Signal.hpp.
|
related |
Definition at line 4049 of file Matrix.hpp.
|
related |
Definition at line 5173 of file HyperVolume.hpp.
|
related |
Definition at line 5182 of file Matrix4d.hpp.
|
related |
Definition at line 5823 of file Matrix3d.hpp.
|
related |
Definition at line 6140 of file Volume.hpp.
|
inline |
Computes the third quartile value from a non sorted range.
| first | A RandomAccessIterator. |
| last | A RandomAccessIterator. |
Definition at line 1230 of file statistics.hpp.
|
inline |
Computes the third quartile value from a non sorted range using a predicate.
| first | A RandomAccessIterator. |
| last | A RandomAccessIterator. |
| pred | a predicate function |
Definition at line 3494 of file statistics.hpp.
|
inline |
Computes the third quartile value from a non sorted range over a mask.
| first | A RandomAccessIterator. |
| last | A RandomAccessIterator. |
| mask_first | An InputIterator of the mask |
| value | Mask value. |
Definition at line 2438 of file statistics.hpp.
| void slip::thomas_inv | ( | RandomAccessIterator1 | diag_first, |
| RandomAccessIterator1 | diag_last, | ||
| RandomAccessIterator1 | up_diag_first, | ||
| RandomAccessIterator1 | up_diag_last, | ||
| RandomAccessIterator1 | low_diag_first, | ||
| RandomAccessIterator1 | low_diag_last, | ||
| RandomAccessIterator2d | Ainv_up, | ||
| RandomAccessIterator2d | Ainv_bot, | ||
| typename slip::lin_alg_traits< typename std::iterator_traits< RandomAccessIterator1 >::value_type >::value_type | precision = typename slip::lin_alg_traits<typename std::iterator_traits<RandomAccessIterator1>::value_type>::value_type(1.0E-6) |
||
| ) |
Invert a tridiagonal squared matrix A with the Thomas method
![\[ \left( \begin{array}{ccccc} d_{1} & u_{1}&0&\cdots&0\\ l_{1} & d_{2} & u_{2}&\ddots&\vdots\\ 0&l_{2}&\ddots&\ddots&0\\ \vdots&\ddots&\ddots&\ddots&u_{n-1}\\ 0&\cdots&0&l_{n-1}&d_{n}\\ \end{array}\right)^{-1} \]](../../form_112.png)
.
| diag_first | RandomAccessIterator to the beginning of the main diagonal. |
| diag_last | RandomAccessIterator to one-past-the-end of the main diagonal. |
| up_diag_first | RandomAccessIterator to the beginning of the first upper diagonal. |
| up_diag_last | RandomAccessIterator to one-past-the-end of the first upper diagonal. |
| low_diag_first | RandomAccessIterator to the beginning of the first lower diagonal. |
| low_diag_last | RandomAccessIterator to one-past-the-end of the first lower diagonal. |
| Ainv_up | RandomAccessIterator2d to the upper_left element of the 2d range of the inverse matrix. |
| Ainv_bot | RandomAccessIterator2d to the one past the bottom_right element of the 2d range of the inverse matrix. |
| precision | 1.0E-6 by default. |
Definition at line 9000 of file linear_algebra.hpp.
| void slip::thomas_inv | ( | const Container2d1 & | A, |
| Container2d2 & | Ainv, | ||
| typename slip::lin_alg_traits< typename Container2d1::value_type >::value_type | precision = typename slip::lin_alg_traits<typename Container2d1::value_type>::value_type(1.0E-6) |
||
| ) |
Invert a tridiagonal squared matrix A with the Thomas method
![\[ \left( \begin{array}{ccccc} d_{1} & u_{1}&0&\cdots&0\\ l_{1} & d_{2} & u_{2}&\ddots&\vdots\\ 0&l_{2}&\ddots&\ddots&0\\ \vdots&\ddots&\ddots&\ddots&u_{n-1}\\ 0&\cdots&0&l_{n-1}&d_{n}\\ \end{array}\right)^{-1} \]](../../form_112.png)
.
| A | 2d container of the matrix to invert. |
| Ainv | 2d container of the matrix the inverse matrix. |
| precision | 1.0E-6 by default. |
Definition at line 9078 of file linear_algebra.hpp.
| void slip::thomas_solve | ( | RandomAccessIterator1 | diag_first, |
| RandomAccessIterator1 | diag_last, | ||
| RandomAccessIterator1 | up_diag_first, | ||
| RandomAccessIterator1 | up_diag_last, | ||
| RandomAccessIterator1 | low_diag_first, | ||
| RandomAccessIterator1 | low_diag_last, | ||
| RandomAccessIterator2 | X_first, | ||
| RandomAccessIterator2 | X_last, | ||
| RandomAccessIterator3 | B_first, | ||
| RandomAccessIterator3 | B_last, | ||
| typename slip::lin_alg_traits< typename std::iterator_traits< RandomAccessIterator1 >::value_type >::value_type | precision = typename slip::lin_alg_traits<typename std::iterator_traits<RandomAccessIterator1>::value_type>::value_type(1.0E-6) |
||
| ) |
Solve the tridiagonal system A*X=B with the Thomas method
![\[ \left( \begin{array}{ccccc} d_{1} & u_{1}&0&\cdots&0\\ l_{1} & d_{2} & u_{2}&\ddots&\vdots\\ 0&l_{2}&\ddots&\ddots&0\\ \vdots&\ddots&\ddots&\ddots&u_{n-1}\\ 0&\cdots&0&l_{n-1}&d_{n}\\ \end{array}\right) \left( \begin{array}{c} x_{1}\\ \vdots\\ \vdots\\ \vdots\\ x_{n}\\ \end{array}\right) = \left( \begin{array}{c} b_{1}\\ \vdots\\ \vdots\\ \vdots\\ b_{n}\\ \end{array}\right) \]](../../form_111.png)
.
| diag_first | RandomAccessIterator to the beginning of the main diagonal. |
| diag_last | RandomAccessIterator to one-past-the-end of the main diagonal. |
| up_diag_first | RandomAccessIterator to the beginning of the first upper diagonal. |
| up_diag_last | RandomAccessIterator to one-past-the-end of the first upper diagonal. |
| low_diag_first | RandomAccessIterator to the beginning of the first lower diagonal. |
| low_diag_last | RandomAccessIterator to one-past-the-end of the first lower diagonal. |
| X_first | RandomAccessIterator to the begenning of the result range. |
| X_last | RandomAccessIterator to one-past-the-end of the result range. |
| B_first | RandomAccessIterator to the begenning of the B range. |
| B_last | RandomAccessIterator to one-past-the-end of the B range. |
| precision | 1.0E-6 by default. |
Definition at line 8795 of file linear_algebra.hpp.
| void slip::thomas_solve | ( | const Container2d & | A, |
| Vector1 & | X, | ||
| const Vector2 & | B, | ||
| typename slip::lin_alg_traits< typename Container2d::value_type >::value_type | precision = typename slip::lin_alg_traits<typename Container2d::value_type>::value_type(1.0E-6) |
||
| ) |
Solve the tridiagonal system Tx=B
![\[ \left( \begin{array}{ccccc} d_{1} & u_{1}&0&\cdots&0\\ l_{1} & d_{2} & u_{2}&\ddots&\vdots\\ 0&l_{2}&\ddots&\ddots&0\\ \vdots&\ddots&\ddots&\ddots&u_{n-1}\\ 0&\cdots&0&l_{n-1}&d_{n}\\ \end{array}\right) \left( \begin{array}{c} x_{1}\\ \vdots\\ \vdots\\ \vdots\\ x_{n}\\ \end{array}\right) = \left( \begin{array}{c} b_{1}\\ \vdots\\ \vdots\\ \vdots\\ b_{n}\\ \end{array}\right) \]](../../form_111.png)
.
Definition at line 8911 of file linear_algebra.hpp.
|
inline |
threshold algorithm
| first | begin InputIterator of the range to threshold |
| last | past-the-end InputIterator of the range to threshold |
| result | begin OutputIterator of the resulting range |
| t_value | threshold value |
| false_value | result value when *first <= t_value |
Definition at line 235 of file threshold.hpp.
|
inline |
Constructs the Toeplitz matrix from given a range.
| first | RandomAccessIterator to the first element of the Toeplitz vector |
| last | RandomAccessIterator to one past-the-end element of the Toeplitz vector |
| A | Toplitz matrix. |
Definition at line 3758 of file linear_algebra.hpp.
| _OutputIterator slip::transform_if | ( | _InputIterator | first, |
| _InputIterator | last, | ||
| _OutputIterator | result, | ||
| _UnaryOperation | unary_op, | ||
| _Predicate | pred | ||
| ) |
Perform an operation on a sequence according to a Predicate.
| first | An input iterator. |
| last | An input iterator. |
| result | An output iterator. |
| unary_op | A unary operator. |
| pred | A predicate. |
Definition at line 308 of file stl_algo_ext.hpp.
| _OutputIterator slip::transform_if | ( | _InputIterator1 | first1, |
| _InputIterator1 | last1, | ||
| _InputIterator2 | first2, | ||
| _OutputIterator | result, | ||
| _BinaryOperation | binary_op, | ||
| _Predicate | pred | ||
| ) |
Perform an operation on corresponding elements of two sequences according to a Predicate.
| first1 | An input iterator. |
| last1 | An input iterator. |
| first2 | An input iterator. |
| result | An output iterator. |
| binary_op | A binary operator. |
| pred | A predicate. |
Definition at line 378 of file stl_algo_ext.hpp.
| _OutputIterator slip::transform_mask_bin | ( | _InputIterator1 | first1, |
| _InputIterator1 | last1, | ||
| _MaskIterator | mask_first, | ||
| _InputIterator2 | first2, | ||
| _OutputIterator | result, | ||
| _BinaryOperation | binary_op, | ||
| typename std::iterator_traits< _MaskIterator >::value_type | value = typename std::iterator_traits<_MaskIterator>::value_type(1) |
||
| ) |
Perform an operation on corresponding elements of two sequences according to a mask sequence.
| first1 | An input iterator. |
| last1 | An input iterator. |
| mask_first | An input iterator. |
| first2 | An input iterator. |
| result | An output iterator. |
| binary_op | A binary operator. |
| value | true value of the mask range. Default is 1. |
Definition at line 240 of file stl_algo_ext.hpp.
| _OutputIterator slip::transform_mask_un | ( | _InputIterator | first, |
| _InputIterator | last, | ||
| _MaskIterator | mask_first, | ||
| _OutputIterator | result, | ||
| _UnaryOperation | unary_op, | ||
| typename std::iterator_traits< _MaskIterator >::value_type | value = typename std::iterator_traits<_MaskIterator>::value_type(1) |
||
| ) |
Perform an operation on a sequence according to a mask sequence.
| first | An input iterator. |
| last | An input iterator. |
| mask_first | An input iterator. |
| result | An output iterator. |
| unary_op | A unary operator. |
| value | true value of the mask range. Default is 1. |
Definition at line 152 of file stl_algo_ext.hpp.
|
inline |
Computes the transpose of a matrix 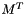 .
.
| M | Matrix container |
| nr1 | The number of rows of M |
| nc1 | The number of columns of M |
| TM | result of the transposition |
| nr2 | The number of rows of TM |
| nc2 | The number of columns of TM |
Definition at line 2516 of file linear_algebra.hpp.
|
inline |
Computes the transpose of a matrix 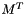 .
.
| M | Matrix container |
| TM | result of the transposition |
Definition at line 2562 of file linear_algebra.hpp.
| void slip::tridiagonal_cholesky | ( | RandomAccessIterator1 | diag_first, |
| RandomAccessIterator1 | diag_last, | ||
| RandomAccessIterator1 | up_diag_first, | ||
| RandomAccessIterator1 | up_diag_last, | ||
| RandomAccessIterator2 | R_diag_first, | ||
| RandomAccessIterator2 | R_diag_last, | ||
| RandomAccessIterator3 | R_low_first, | ||
| RandomAccessIterator3 | R_low_last | ||
| ) |
Tridiagonal symmetric positive decomposition
![\[ \left( \begin{array}{ccccc} d_{1} & u_{1}&0&\cdots&0\\ \bar{u}_{1} & d_{2} & u_{2}&\ddots&\vdots\\ 0&\bar{u}_{2}&\ddots&\ddots&0\\ \vdots&\ddots&\ddots&\ddots&u_{n-1}\\ 0&\cdots&0&\bar{u}_{n-1}&d_{n}\\ \end{array}\right) = \left( \begin{array}{ccccc} d_{1} & 0&\cdots&\cdots&0\\ r_1 & d_{2} & \ddots&&\vdots\\ 0&r_2&\ddots&\ddots&\vdots\\ \vdots&\ddots&\ddots&\ddots&0\\ 0&\cdots&0&r_{n-1}&d_{n}\\ \end{array}\right) \left( \begin{array}{ccccc} d_{1} & \bar{r}_{1}&0&\cdots&0\\ 0 & d_{2} & \bar{r}_{2}&\ddots&\vdots\\ \vdots&\ddots&\ddots&\ddots&0\\ \vdots&&\ddots&\ddots&\bar{r}_{n-1}\\ 0&\cdots&\cdots&0&d_{n}\\ \end{array}\right) \]](../../form_113.png)
where: 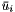 is the conjugate of
is the conjugate of 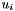 and
and 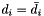 .
.
| diag_first | RandomAccessIterator to the beginning of the main diagonal. |
| diag_last | RandomAccessIterator to one-past-the-end of the main diagonal. |
| up_diag_first | RandomAccessIterator to the beginning of the first upper diagonal. |
| up_diag_last | RandomAccessIterator to one-past-the-end of the first upper diagonal. |
| R_diag_first | RandomAccessIterator to the beginning of the first diagonal of R. |
| R_diag_last | RandomAccessIterator to one-past-the-end of the first diagonal of R. |
| R_low_first | RandomAccessIterator to the beginning of the first lower diagonal. |
| R_low_last | RandomAccessIterator to one-past-the-end of the first lower diagonal. |
Definition at line 9203 of file linear_algebra.hpp.
| void slip::tridiagonal_cholesky_inv | ( | RandomAccessIterator1 | diag_first, |
| RandomAccessIterator1 | diag_last, | ||
| RandomAccessIterator1 | up_diag_first, | ||
| RandomAccessIterator1 | up_diag_last, | ||
| RandomAccessIterator2d | Ainv_up, | ||
| RandomAccessIterator2d | Ainv_bot | ||
| ) |
Invert the tridiagonal symmetric positive definite system T:
![\[ \left( \begin{array}{ccccc} d_{1} & u_{1}&0&\cdots&0\\ \bar{u}_{1} & d_{2} & u_{2}&\ddots&\vdots\\ 0&\bar{u}_{2}&\ddots&\ddots&0\\ \vdots&\ddots&\ddots&\ddots&u_{n-1}\\ 0&\cdots&0&\bar{u}_{n-1}&d_{n}\\ \end{array}\right)^{-1} \]](../../form_118.png)
where: 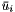 is the conjugate of
is the conjugate of 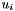 and
and 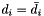 .
.
| diag_first | RandomAccessIterator to the beginning of the main diagonal. |
| diag_last | RandomAccessIterator to one-past-the-end of the main diagonal. |
| up_diag_first | RandomAccessIterator to the beginning of the first upper diagonal. |
| up_diag_last | RandomAccessIterator to one-past-the-end of the first upper diagonal. |
| Ainv_up | RandomAccessIterator2d to the upper_left element of the 2d range of the inverse matrix. |
| Ainv_bot | RandomAccessIterator2d to the one past the bottom_right element of the 2d range of the inverse matrix. |
Definition at line 9516 of file linear_algebra.hpp.
| void slip::tridiagonal_cholesky_inv | ( | const Container2d1 & | A, |
| Container2d2 & | Ainv | ||
| ) |
Invert the tridiagonal symmetric positive definite system T:
![\[ \left( \begin{array}{ccccc} d_{1} & u_{1}&0&\cdots&0\\ \bar{u}_{1} & d_{2} & u_{2}&\ddots&\vdots\\ 0&\bar{u}_{2}&\ddots&\ddots&0\\ \vdots&\ddots&\ddots&\ddots&u_{n-1}\\ 0&\cdots&0&\bar{u}_{n-1}&d_{n}\\ \end{array}\right)^{-1} \]](../../form_118.png)
where: 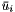 is the conjugate of
is the conjugate of 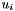 and
and 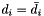 .
.
| A | 2d container of the matrix to invert. |
| Ainv | 2d container of the matrix the inverse matrix. |
Definition at line 9589 of file linear_algebra.hpp.
| void slip::tridiagonal_cholesky_solve | ( | RandomAccessIterator1 | diag_first, |
| RandomAccessIterator1 | diag_last, | ||
| RandomAccessIterator1 | up_diag_first, | ||
| RandomAccessIterator1 | up_diag_last, | ||
| RandomAccessIterator2 | X_first, | ||
| RandomAccessIterator2 | X_last, | ||
| RandomAccessIterator3 | B_first, | ||
| RandomAccessIterator3 | B_last | ||
| ) |
Solve the tridiagonal symmetric positive definite system T*X=B with the Cholesky method
![\[ \left( \begin{array}{ccccc} d_{1} & u_{1}&0&\cdots&0\\ \bar{u}_{1} & d_{2} & u_{2}&\ddots&\vdots\\ 0&\bar{u}_{2}&\ddots&\ddots&0\\ \vdots&\ddots&\ddots&\ddots&u_{n-1}\\ 0&\cdots&0&\bar{u}_{n-1}&d_{n}\\ \end{array}\right) \left( \begin{array}{c} x_{1}\\ \vdots\\ \vdots\\ \vdots\\ x_{n}\\ \end{array}\right) = \left( \begin{array}{c} b_{1}\\ \vdots\\ \vdots\\ \vdots\\ b_{n}\\ \end{array}\right) \]](../../form_117.png)
where: 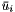 is the conjugate of
is the conjugate of  and
and 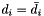 .
.
| diag_first | RandomAccessIterator to the beginning of the main diagonal. |
| diag_last | RandomAccessIterator to one-past-the-end of the main diagonal. |
| up_diag_first | RandomAccessIterator to the beginning of the first upper diagonal. |
| up_diag_last | RandomAccessIterator to one-past-the-end of the first upper diagonal. |
| X_first | RandomAccessIterator to the begenning of the result range. |
| X_last | RandomAccessIterator to one-past-the-end of the result range. |
| B_first | RandomAccessIterator to the begenning of the B range. |
| B_last | RandomAccessIterator to one-past-the-end of the B range. |
Definition at line 9321 of file linear_algebra.hpp.
| void slip::tridiagonal_cholesky_solve | ( | const Container2d & | A, |
| Vector1 & | X, | ||
| const Vector2 & | B | ||
| ) |
Solve the tridiagonal symmetric positive definite system T*X=B with the Cholesky method
![\[ \left( \begin{array}{ccccc} d_{1} & u_{1}&0&\cdots&0\\ \bar{u}_{1} & d_{2} & u_{2}&\ddots&\vdots\\ 0&\bar{u}_{2}&\ddots&\ddots&0\\ \vdots&\ddots&\ddots&\ddots&u_{n-1}\\ 0&\cdots&0&\bar{u}_{n-1}&d_{n}\\ \end{array}\right) \left( \begin{array}{c} x_{1}\\ \vdots\\ \vdots\\ \vdots\\ x_{n}\\ \end{array}\right) = \left( \begin{array}{c} b_{1}\\ \vdots\\ \vdots\\ \vdots\\ b_{n}\\ \end{array}\right) \]](../../form_117.png)
where: 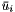 is the conjugate of
is the conjugate of 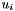 and
and 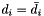 .
.
| A | The matrix A. |
| X | The vector X. |
| B | The vector to match B. |
Definition at line 9437 of file linear_algebra.hpp.
| void slip::tridiagonal_lu | ( | RandomAccessIterator1 | diag_first, |
| RandomAccessIterator1 | diag_last, | ||
| RandomAccessIterator1 | up_diag_first, | ||
| RandomAccessIterator1 | up_diag_last, | ||
| RandomAccessIterator1 | low_diag_first, | ||
| RandomAccessIterator1 | low_diag_last, | ||
| RandomAccessIterator2 | L_low_first, | ||
| RandomAccessIterator2 | L_low_last, | ||
| RandomAccessIterator3 | U_up_first, | ||
| RandomAccessIterator3 | U_up_last, | ||
| typename slip::lin_alg_traits< typename std::iterator_traits< RandomAccessIterator1 >::value_type >::value_type | precision = typename slip::lin_alg_traits<typename std::iterator_traits<RandomAccessIterator1>::value_type>::value_type(1.0E-6) |
||
| ) |
Computes the LU decomposition for a tridiagonal matrix
![\[ \left( \begin{array}{ccccc} d_{1} & u_{1}&0&\cdots&0\\ l_{1} & d_{2} & u_{2}&\ddots&\vdots\\ 0&l_{2}&\ddots&\ddots&0\\ \vdots&\ddots&\ddots&\ddots&u_{n-1}\\ 0&\cdots&0&l_{n-1}&d_{n}\\ \end{array}\right) = \left( \begin{array}{ccccc} 1 & 0&\cdots&\cdots&0\\ ll_1 & 1 & \ddots&&\vdots\\ 0&ll_2&\ddots&\ddots&\vdots\\ \vdots&\ddots&\ddots&\ddots&0\\ 0&\cdots&0&ll_{n-1}&1\\ \end{array}\right) \left( \begin{array}{ccccc} du_{1} & uu_{1}&0&\cdots&0\\ 0 & du_{2} & uu_{2}&\ddots&\vdots\\ \vdots&\ddots&\ddots&\ddots&0\\ \vdots&&\ddots&\ddots&uu_{n-1}\\ 0&\cdots&\cdots&0&du_{n}\\ \end{array}\right) \]](../../form_102.png)
.
| diag_first | RandomAccessIterator to the beginning of the main diagonal. |
| diag_last | RandomAccessIterator to one-past-the-end of the main diagonal. |
| up_diag_first | RandomAccessIterator to the beginning of the first upper diagonal. |
| up_diag_last | RandomAccessIterator to one-past-the-end of the first upper diagonal. |
| low_diag_first | RandomAccessIterator to the beginning of the first lower diagonal. |
| low_diag_last | RandomAccessIterator to one-past-the-end of the first lower diagonal. |
| L_low_first | RandomAccessIterator to the beginning of the first element of the lower diagonal of L. |
| L_low_last | RandomAccessIterator to one-past-the-end element of the lower diagonal of L. |
| U_up_first | RandomAccessIterator to the beginning of the first element of the upper diagonal of U. |
| U_up_last | RandomAccessIterator to one-past-the-end of the first element of the upper diagonal of U. |
| precision | 1.0E-6 by default. |
Definition at line 7846 of file linear_algebra.hpp.
|
inline |
Computes the transpose left multiplication:
![\[R = V^T M\]](../../form_65.png)
.
| V_first | RandomAccessIterator to the first element of the Vector. |
| V_last | RandomAccessIterator to one-past-the-end element of the vector. |
| M_up | RandomAccessIterator2d to the upper_left matrix element. |
| M_bot | RandomAccessIterator2d to the bottom_right matrix element. |
| result_first | RandomAccessIterator to the first element of the Vector R. |
| result_last | RandomAccessIterator to one-past-the-end element of the vector R. |
Definition at line 1189 of file linear_algebra.hpp.
|
inline |
Computes the transpose left multiplication:
![\[R = V^T M\]](../../form_65.png)
.
Definition at line 1237 of file linear_algebra.hpp.
|
inline |
Computes the unbiased autocorrelations from lag -(last-first) to (last-first) of a range [first,last).
| first | A RandomAccessIterator to the data. |
| last | A RandomAccessIterator to the data. |
| auto_first | A RandomAccessIterator to the autocorrelations range. |
| auto_last | A RandomAccessIterator to the autocorrelations range. |
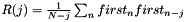
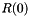 corresponds the energy of the data
corresponds the energy of the dataDefinition at line 1689 of file correlation.hpp.
|
inline |
Computes the unbiased autocovariance from lag -(last-first) to 0 of a range [first,last).
| first | A RandomAccessIterator to the data. |
| last | A RandomAccessIterator to the data. |
| auto_first | A RandomAccessIterator to the autocorrelations range. |
| auto_last | A RandomAccessIterator to the autocorrelations range. |
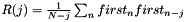
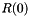 corresponds the energy of the data
corresponds the energy of the dataDefinition at line 1860 of file correlation.hpp.
|
inline |
Computes the unbiased covariance of a two sequences
![\[\frac{1}{n-1}\sum_i (x_i-\overline{x})(y_i-\overline{y})\]](../../form_202.png)
.
| first | An InputIterator. |
| last | An InputIterator. |
| first2 | An InputIterator. |
| mean1 | The mean of the first container. |
| mean2 | The mean of the second container. |
Definition at line 488 of file statistics.hpp.
|
inline |
Computes the unbiased covariance of a two sequences using a predicate on the first one
![\[\frac{1}{n-1}\sum_i (x_i-\overline{x})(y_i-\overline{y})\]](../../form_202.png)
.
| first | An InputIterator. |
| last | An InputIterator. |
| first2 | An InputIterator. |
| mean1 | The mean of the first range using the predicate. |
| mean2 | The mean of the second range using the predicate. |
| pred | a predicate function |
Definition at line 2827 of file statistics.hpp.
|
inline |
Computes the unbiased covariance of a two sequences over a mask
![\[\frac{1}{n-1}\sum_i (x_i-\overline{x})(y_i-\overline{y})\]](../../form_202.png)
.
| first | An InputIterator. |
| last | An InputIterator. |
| first2 | An InputIterator. |
| mask_first | An InputIterator on the mask |
| mean1 | The mean of the first range over the mask. |
| mean2 | The mean of the second range over the mask. |
| value | Mask value. |
Definition at line 1664 of file statistics.hpp.
|
inline |
Computes the unbiased kurtosis of a range
![\[\frac{(n+1)n(n-1)}{(n-2)(n-3)}\frac{\sum_i (x_i-\overline{x})^4}{\left[\sum_i (x_i-\overline{x})^2\right]^2}- \frac{3(n-1)^2}{(n-2)(n-3)} + 3\]](../../form_208.png)
A high kurtosis distribution has a sharper peak and longer, fatter tails, while a low kurtosis distribution has a more rounded peak and shorter thinner tails.
| first | An InputIterator. |
| last | An InputIterator. |
| mean | The mean of the container itself. |
Definition at line 715 of file statistics.hpp.
|
inline |
Computes the unbiased kurtosis of a range using a predicate
![\[\frac{(n+1)n(n-1)}{(n-2)(n-3)}\frac{\sum_i (x_i-\overline{x})^4}{\left[\sum_i (x_i-\overline{x})^2\right]^2}- \frac{3(n-1)^2}{(n-2)(n-3)} + 3\]](../../form_208.png)
A high kurtosis distribution has a sharper peak and longer, fatter tails, while a low kurtosis distribution has a more rounded peak and shorter thinner tails.
| first | An InputIterator. |
| last | An InputIterator. |
| mean | The mean of the range itself using the predicate. |
| pred | a predicate function |
Definition at line 3121 of file statistics.hpp.
|
inline |
Computes the unbiased kurtosis of a range over a mask
![\[\frac{(n+1)n(n-1)}{(n-2)(n-3)}\frac{\sum_i (x_i-\overline{x})^4}{\left[\sum_i (x_i-\overline{x})^2\right]^2}- \frac{3(n-1)^2}{(n-2)(n-3)} + 3\]](../../form_208.png)
A high kurtosis distribution has a sharper peak and longer, fatter tails, while a low kurtosis distribution has a more rounded peak and shorter thinner tails.
| first | An InputIterator. |
| last | An InputIterator. |
| mask_first | An InputIterator on the mask |
| mean | The mean of the range itself over the mask. |
| value | Mask value. |
Definition at line 1971 of file statistics.hpp.
|
inline |
Computes the unbiased skewness of a range
![\[\frac{n}{(n-1)(n-2)}\frac{\sum_i (x_i-\overline{x})^3}{\left(\sqrt{\frac{1}{n-1}\sum_i (x_i-\overline{x})^2}\right)^3}\]](../../form_210.png)
skewness is a measure of the asymmetry of the probability distribution of a real-valued random variable.
| first | An InputIterator. |
| last | An InputIterator. |
| std_dev | The standard deviation of the container itself. |
Definition at line 820 of file statistics.hpp.
|
inline |
Computes the unbiased skewness of a range using a predicate
![\[\frac{n}{(n-1)(n-2)}\frac{\sum_i (x_i-\overline{x})^3}{\left(\sqrt{\frac{1}{n-1}\sum_i (x_i-\overline{x})^2}\right)^3}\]](../../form_210.png)
skewness is a measure of the asymmetry of the probability distribution of a real-valued random variable.
| first | An InputIterator. |
| last | An InputIterator. |
| mean | The mean of the range itself using the predicate. |
| pred | a predicate function |
Definition at line 3250 of file statistics.hpp.
|
inline |
Computes the unbiased skewness of a range over a mask
![\[\frac{n}{(n-1)(n-2)}\frac{\sum_i (x_i-\overline{x})^3}{\left(\sqrt{\frac{1}{n-1}\sum_i (x_i-\overline{x})^2}\right)^3}\]](../../form_210.png)
skewness is a measure of the asymmetry of the probability distribution of a real-valued random variable.
| first | An InputIterator. |
| last | An InputIterator. |
| mask_first | An InputIterator on the mask |
| mean | The mean of the range itself over the mask. |
| value | Mask value. |
Definition at line 2118 of file statistics.hpp.
| void slip::unbiased_statistics | ( | InputIterator | first, |
| InputIterator | last, | ||
| slip::Statistics< T > & | statistic | ||
| ) |
compute all unbiased statistics of a range
| first | An InputIterator. |
| last | An InputIterator. |
| statistic | slip::statistics |
Definition at line 3714 of file statistics.hpp.
| void slip::unbiased_statistics_if | ( | InputIterator | first, |
| InputIterator | last, | ||
| slip::Statistics< T > & | statistic, | ||
| Predicate | pred | ||
| ) |
compute all unbiased statistics of a range according to a preidcate.
| first | An InputIterator. |
| last | An InputIterator. |
| statistic | slip::statistics |
| pred | a predicate function. |
Definition at line 4022 of file statistics.hpp.
| void slip::unbiased_statistics_mask | ( | InputIterator | first, |
| InputIterator | last, | ||
| MaskIterator | mask_first, | ||
| slip::Statistics< T > & | statistic, | ||
| typename std::iterator_traits< MaskIterator >::value_type | value = typename std::iterator_traits<MaskIterator>::value_type(1) |
||
| ) |
compute all unbiased statistics of a range according to a mask range.
| first | An InputIterator. |
| last | An InputIterator. |
| mask_first | An InputIterator of the mask |
| statistic | slip::Statistics which contains all the unbiased statistics of the range. |
| value | Mask value. |
Definition at line 3884 of file statistics.hpp.
|
inline |
Computes the unbiased standard deviation of a range
![\[\sqrt{\frac{1}{n-1}\sum_i (x_i-\overline{x})^2}\]](../../form_206.png)
.
| first | An InputIterator. |
| last | An InputIterator. |
| mean | The mean of the container itself. |
Definition at line 626 of file statistics.hpp.
|
inline |
Computes the unbiased standard deviation of a range using a predicate
![\[\sqrt{\frac{1}{n-1}\sum_i (x_i-\overline{x})^2}\]](../../form_206.png)
.
| first | An InputIterator. |
| last | An InputIterator. |
| mean | The mean of the range itself using the predicate. |
| pred | a predicate function |
Definition at line 3011 of file statistics.hpp.
|
inline |
Computes the unbiased standard deviation of a range over a mask
![\[\sqrt{\frac{1}{n-1}\sum_i (x_i-\overline{x})^2}\]](../../form_206.png)
.
| first | An InputIterator. |
| last | An InputIterator. |
| mask_first | An InputIterator on the mask |
| mean | The mean of the range itself over the mask. |
| value | Mask value. |
Definition at line 1855 of file statistics.hpp.
|
inline |
Computes the unbiased variance of a range
![\[\frac{1}{n-1}\sum_i (x_i-\overline{x})^2\]](../../form_204.png)
.
| first | An InputIterator. |
| last | An InputIterator. |
| mean | The mean of the container itself. |
Definition at line 566 of file statistics.hpp.
|
inline |
Computes the unbiased variance of a range using a predicate
![\[\frac{1}{n-1}\sum_i (x_i-\overline{x})^2\]](../../form_204.png)
.
| first | An InputIterator. |
| last | An InputIterator. |
| mean | The mean of the range itself using the predicate. |
| pred | a predicate function |
Definition at line 2928 of file statistics.hpp.
|
inline |
Computes the unbiased variance of a range over a mask
![\[\frac{1}{n-1}\sum_i (x_i-\overline{x})^2\]](../../form_204.png)
.
| first | An InputIterator. |
| last | An InputIterator. |
| mask_first | An InputIterator on the mask |
| mean | The mean of the range itself over the mask. |
| value | Mask value. |
Definition at line 1770 of file statistics.hpp.
|
inline |
Solve the linear system L*X=B when L is unit p lower banded
![\[ \left( \begin{array}{ccccccc} 1 & 0&\cdots&\cdots&\cdots&\cdots&0\\ l_{2,1} & 1 & \ddots&&&&\vdots\\ \vdots&\ddots&\ddots&\ddots&&&\vdots\\ l_{p+1,1}&&\ddots&\ddots&\ddots&&\vdots\\ 0&\ddots&&\ddots&\ddots&\ddots&\vdots\\ \vdots&\ddots&\ddots&&\ddots&1&0\\ 0&\cdots&0&l_{n,n-q}&\cdots&l_{n,n-1}&1\\ \end{array}\right) \left( \begin{array}{c} x_{1}\\ x_{2}\\ \vdots\\ x_{n}\\ \end{array}\right) = \left( \begin{array}{c} b_{1}\\ b_{2}\\ \vdots\\ b_{n}\\ \end{array}\right) \]](../../form_101.png)
.
| L_up | 2D iterator corresponding to the upper_left element of the matrix L |
| L_bot | 2D iterator corresponding to one past-the-end bottom_right of the matrix L |
| p | Width of the lower band. |
| X_first | RandomAccessIterator point to the first element of X. |
| X_last | RandomAccessIterator point one-past-the-end element of X. |
| B_first | RandomAccessIterator point to the first element of B. |
| B_last | RandomAccessIterator to one-past-the-end element of B. |
Definition at line 7400 of file linear_algebra.hpp.
| void slip::unit_lower_bidiagonal_inv | ( | RandomAccessIterator1 | low_diag_first, |
| RandomAccessIterator1 | low_diag_last, | ||
| RandomAccessIterator2d | Ainv_up, | ||
| RandomAccessIterator2d | Ainv_bot | ||
| ) |
Invert a lower unit bidiagonal matrix:
![\[ \left( \begin{array}{ccccc} 1 & 0&\cdots&\cdots&0\\ l_{1} & 1 & \ddots&&\vdots\\ 0&l_{2}&\ddots&\ddots&\vdots\\ \vdots&\ddots&\ddots&\ddots&0\\ 0&\cdots&0&l_{n-1}&1\\ \end{array}\right)^{-1} \]](../../form_104.png)
.
| low_diag_first | RandomAccessIterator to the beginning of the first lower diagonal. |
| low_diag_last | RandomAccessIterator to one-past-the-end of the first lower diagonal. |
| Ainv_up | RandomAccessIterator2d to the upper_left element of the 2d range of the inverse matrix. |
| Ainv_bot | RandomAccessIterator2d to the one past the bottom_right element of the 2d range of the inverse matrix. |
Definition at line 8007 of file linear_algebra.hpp.
| void slip::unit_lower_bidiagonal_solve | ( | RandomAccessIterator1 | low_diag_first, |
| RandomAccessIterator1 | low_diag_last, | ||
| RandomAccessIterator2 | X_first, | ||
| RandomAccessIterator2 | X_last, | ||
| RandomAccessIterator3 | B_first, | ||
| RandomAccessIterator3 | B_last | ||
| ) |
solve Ax = B with A unit lower bidiagonal
![\[ \left( \begin{array}{ccccc} 1 & 0&\cdots&\cdots&0\\ ll_1 & 1 & \ddots&&\vdots\\ 0&ll_2&\ddots&\ddots&\vdots\\ \vdots&\ddots&\ddots&\ddots&0\\ 0&\cdots&0&ll_{n-1}&1\\ \end{array}\right) \left( \begin{array}{c} x_{1}\\ x_{2}\\ \vdots\\ x_n\\ \end{array}\right) = \left( \begin{array}{c} b_{1}\\ b_{2}\\ \vdots\\ b_n\\ \end{array}\right) \]](../../form_103.png)
| low_diag_first | RandomAccessIterator to the first element of the lower diagonal. |
| low_diag_last | RandomAccessIterator to one-past-the-end element of the lower diagonal. |
| X_first | RandomAccessIterator to the begenning of the result range. |
| X_last | RandomAccessIterator to one-past-the-end of the result range. |
| B_first | RandomAccessIterator to the begenning of the B range. |
| B_last | RandomAccessIterator to one-past-the-end of the B range. |
Definition at line 7946 of file linear_algebra.hpp.
|
inline |
Solve the linear system L*X=B when L is unit lower triangular
![\[ \left( \begin{array}{cccc} 1 & 0&\cdots&0\\ l_{2,1} & 1 & \ddots&\vdots\\ \vdots&\ddots&\ddots&0\\ l_{n,1}&\cdots&l_{n,n-1}&1\\ \end{array}\right) \left( \begin{array}{c} x_{1}\\ x_{2}\\ \vdots\\ x_{n}\\ \end{array}\right) = \left( \begin{array}{c} b_{1}\\ b_{2}\\ \vdots\\ b_{n}\\ \end{array}\right) \]](../../form_94.png)
.
| L_up | 2D iterator corresponding to the upper_left element of the matrix L |
| L_bot | 2D iterator corresponding to one past-the-end bottom_right of the matrix L |
| X_first | RandomAccessIterator point to the first element of X. |
| X_last | RandomAccessIterator point one-past-the-end element of X. |
| B_first | RandomAccessIterator point to the first element of B. |
| B_last | RandomAccessIterator to one-past-the-end element of B. |
Definition at line 6539 of file linear_algebra.hpp.
|
inline |
Solve the linear system L*X=B when L is unit lower triangular
![\[ \left( \begin{array}{cccc} 1 & 0&\cdots&0\\ l_{2,1} & 1 & \ddots&\vdots\\ \vdots&\ddots&\ddots&0\\ l_{n,1}&\cdots&l_{n,n-1}&1\\ \end{array}\right) \left( \begin{array}{c} x_{1}\\ x_{2}\\ \vdots\\ x_{n}\\ \end{array}\right) = \left( \begin{array}{c} b_{1}\\ b_{2}\\ \vdots\\ b_{n}\\ \end{array}\right) \]](../../form_94.png)
.
| L | 2D container |
| X | 1D container |
| B | 1D container |
Definition at line 6631 of file linear_algebra.hpp.
|
inline |
Solve the linear system U*X=B when U is unit q width upper banded
![\[ \left( \begin{array}{cccccc} 1 & \cdots&u_{1,q+1}&0&\cdots&0\\ 0 & 1 &\ddots&\ddots&\ddots&\vdots\\ \vdots&\ddots&\ddots&\ddots&\ddots&0\\ \vdots&&\ddots&\ddots&\ddots&u_{n-q,n}\\ \vdots&&&\ddots&\ddots&\vdots\\ 0&\cdots&\cdots&\cdots&0&1\\ \end{array}\right) \left( \begin{array}{c} x_{1}\\ x_{2}\\ \vdots\\ x_{n}\\ \end{array}\right) = \left( \begin{array}{c} b_{1}\\ b_{2}\\ \vdots\\ b_{n}\\ \end{array}\right) \]](../../form_99.png)
.
| U_up | 2D iterator corresponding to the upper_left element of the matrix U |
| U_bot | 2D iterator corresponding to one past-the-end bottom_right of the matrix U |
| q | Size of the upper band. |
| X_first | RandomAccessIterator point to the first element of X. |
| X_last | RandomAccessIterator point one-past-the-end element of X. |
| B_first | RandomAccessIterator point to the first element of B. |
| B_last | RandomAccessIterator to one-past-the-end element of B. |
| precision |
Definition at line 7154 of file linear_algebra.hpp.
| void slip::unit_upper_bidiagonal_inv | ( | RandomAccessIterator1 | up_diag_first, |
| RandomAccessIterator1 | up_diag_last, | ||
| RandomAccessIterator2d | Ainv_up, | ||
| RandomAccessIterator2d | Ainv_bot | ||
| ) |
Invert an unit upper bidiagonal matrix:
![\[ \left( \begin{array}{ccccc} 1 & u_{1}&0&\cdots&0\\ 0 & 1 & u_{2}&\ddots&\vdots\\ \vdots&\ddots&\ddots&\ddots&0\\ \vdots&&\ddots&\ddots&u_{n-1}\\ 0&\cdots&\cdots&0&1\\ \end{array}\right)^{-1} \]](../../form_110.png)
.
| up_diag_first | RandomAccessIterator to the beginning of the first upper diagonal. |
| up_diag_last | RandomAccessIterator to one-past-the-end of the first upper diagonal. |
| Ainv_up | RandomAccessIterator2d to the upper_left element of the 2d range of the inverse matrix. |
| Ainv_bot | RandomAccessIterator2d to the one past the bottom_right element of the 2d range of the inverse matrix. |
Definition at line 8690 of file linear_algebra.hpp.
| void slip::unit_upper_bidiagonal_solve | ( | RandomAccessIterator1 | up_diag_first, |
| RandomAccessIterator1 | up_diag_last, | ||
| RandomAccessIterator2 | X_first, | ||
| RandomAccessIterator2 | X_last, | ||
| RandomAccessIterator3 | B_first, | ||
| RandomAccessIterator3 | B_last | ||
| ) |
solve Ax = B with A unit upper bidiagonal
![\[ \left( \begin{array}{ccccc} 1 & uu_1&0&\cdots&0\\ 0 & \ddots & \ddots&\ddots&\vdots\\ \vdots&\ddots&\ddots&\ddots&0\\ \vdots&&\ddots&\ddots&uu_{n-1}\\ 0&\cdots&\cdots&0&1\\ \end{array}\right) \left( \begin{array}{c} x_{1}\\ x_{2}\\ \vdots\\ x_n\\ \end{array}\right) = \left( \begin{array}{c} b_{1}\\ b_{2}\\ \vdots\\ b_n\\ \end{array}\right) \]](../../form_109.png)
| up_diag_first | RandomAccessIterator to the first element of the upper diagonal. |
| up_diag_last | RandomAccessIterator to one-past-the-end element of the upper diagonal. |
| X_first | RandomAccessIterator to the begenning of the result range. |
| X_last | RandomAccessIterator to one-past-the-end of the result range. |
| B_first | RandomAccessIterator to the begenning of the B range. |
| B_last | RandomAccessIterator to one-past-the-end of the B range. |
Definition at line 8620 of file linear_algebra.hpp.
|
inline |
Solve the linear system U*X=B when U is unit upper triangular
![\[ \left( \begin{array}{cccc} 1 & u_{1,2}&\cdots&u_{1,n}\\ 0 & 1 & \ddots&\vdots\\ \vdots&\ddots&\ddots&u_{n-1,n}\\ 0&\cdots&0&1\\ \end{array}\right) \left( \begin{array}{c} x_{1}\\ x_{2}\\ \vdots\\ x_{n}\\ \end{array}\right) = \left( \begin{array}{c} b_{1}\\ b_{2}\\ \vdots\\ b_{n}\\ \end{array}\right) \]](../../form_93.png)
.
| U_up | 2D iterator corresponding to the upper_left element of the matrix U |
| U_bot | 2D iterator corresponding to one past-the-end bottom_right of the matrix U |
| X_first | RandomAccessIterator point to the first element of X. |
| X_last | RandomAccessIterator point one-past-the-end element of X. |
| B_first | RandomAccessIterator point to the first element of B. |
| B_last | RandomAccessIterator to one-past-the-end element of B. |
Definition at line 6363 of file linear_algebra.hpp.
|
inline |
Solve the linear system U*X=B when U is unit upper triangular
![\[ \left( \begin{array}{cccc} 1 & u_{1,2}&\cdots&u_{1,n}\\ 0 & 1 & \ddots&\vdots\\ \vdots&\ddots&\ddots&u_{n-1,n}\\ 0&\cdots&0&1\\ \end{array}\right) \left( \begin{array}{c} x_{1}\\ x_{2}\\ \vdots\\ x_{n}\\ \end{array}\right) = \left( \begin{array}{c} b_{1}\\ b_{2}\\ \vdots\\ b_{n}\\ \end{array}\right) \]](../../form_93.png)
.
| U | 2D container |
| X | 1D container |
| B | 1D container |
Definition at line 6461 of file linear_algebra.hpp.
| void slip::update_border | ( | _II | first, |
| _II | last, | ||
| const slip::BORDER_TREATMENT | border, | ||
| const std::size_t | b_size = 1 |
||
| ) |
Updates the border of the range [first,last) according to b_size and border condition: border.
| first | RandomAccessIterator or RandomAccessIterator2d or RandomAccessIterator3d. |
| last | RandomAccessIterator or RandomAccessIterator2d or RandomAccessIterator3d. |
| border | slip::BORDER_TREATMENT border condition. |
| b_size | Size of the border (1 by default). |
Definition at line 802 of file border_treatment.hpp.
|
inline |
Solve the linear system U*X=B when U is q width upper banded
![\[ \left( \begin{array}{cccccc} u_{1,1} & \cdots&u_{1,q+1}&0&\cdots&0\\ 0 & u_{2,2} &\ddots&\ddots&\ddots&\vdots\\ \vdots&\ddots&\ddots&\ddots&\ddots&0\\ \vdots&&\ddots&\ddots&\ddots&u_{n-q,n}\\ \vdots&&&\ddots&\ddots&\vdots\\ 0&\cdots&\cdots&\cdots&0&u_{n,n}\\ \end{array}\right) \left( \begin{array}{c} x_{1}\\ x_{2}\\ \vdots\\ x_{n}\\ \end{array}\right) = \left( \begin{array}{c} b_{1}\\ b_{2}\\ \vdots\\ b_{n}\\ \end{array}\right) \]](../../form_98.png)
.
| U_up | 2D iterator corresponding to the upper_left element of the matrix U |
| U_bot | 2D iterator corresponding to one past-the-end bottom_right of the matrix U |
| q | Size of the upper band. |
| X_first | RandomAccessIterator point to the first element of X. |
| X_last | RandomAccessIterator point one-past-the-end element of X. |
| B_first | RandomAccessIterator point to the first element of B. |
| B_last | RandomAccessIterator to one-past-the-end element of B. |
| precision |
Definition at line 7025 of file linear_algebra.hpp.
| void slip::upper_bidiagonal_inv | ( | RandomAccessIterator1 | diag_first, |
| RandomAccessIterator1 | diag_last, | ||
| RandomAccessIterator1 | up_diag_first, | ||
| RandomAccessIterator1 | up_diag_last, | ||
| RandomAccessIterator2d | Ainv_up, | ||
| RandomAccessIterator2d | Ainv_bot, | ||
| typename slip::lin_alg_traits< typename std::iterator_traits< RandomAccessIterator1 >::value_type >::value_type | precision = typename slip::lin_alg_traits<typename std::iterator_traits<RandomAccessIterator1>::value_type>::value_type(1.0E-6) |
||
| ) |
Invert an upper bidiagonal squared matrix
![\[ \left( \begin{array}{ccccc} d_{1} & u_{1}&0&\cdots&0\\ 0 & d_{2} & u_{2}&\ddots&\vdots\\ \vdots&\ddots&\ddots&\ddots&0\\ \vdots&\ddots&\ddots&\ddots&u_{n-1}\\ 0&\cdots&\cdots&0&d_{n}\\ \end{array}\right)^{-1} \]](../../form_108.png)
.
| diag_first | RandomAccessIterator to the beginning of the main diagonal. |
| diag_last | RandomAccessIterator to one-past-the-end of the main diagonal. |
| up_diag_first | RandomAccessIterator to the beginning of the first upper diagonal. |
| up_diag_last | RandomAccessIterator to one-past-the-end of the first upper diagonal. |
| Ainv_up | RandomAccessIterator2d to the upper_left element of the 2d range of the inverse matrix. |
| Ainv_bot | RandomAccessIterator2d to the one past the bottom_right element of the 2d range of the inverse matrix. |
| precision | 1.0E-6 by default. |
Definition at line 8451 of file linear_algebra.hpp.
| void slip::upper_bidiagonal_inv | ( | const Container2d1 & | A, |
| Container2d2 & | Ainv, | ||
| typename slip::lin_alg_traits< typename Container2d1::value_type >::value_type | precision = typename slip::lin_alg_traits<typename Container2d1::value_type>::value_type(1.0E-6) |
||
| ) |
Invert an upper bidiagonal squared matrix
![\[ \left( \begin{array}{ccccc} d_{1} & u_{1}&0&\cdots&0\\ 0 & d_{2} & u_{2}&\ddots&\vdots\\ \vdots&\ddots&\ddots&\ddots&0\\ \vdots&\ddots&\ddots&\ddots&u_{n-1}\\ 0&\cdots&\cdots&0&d_{n}\\ \end{array}\right)^{-1} \]](../../form_108.png)
.
| A | 2d container of the matrix to invert. |
| Ainv | 2d container of the matrix the inverse matrix. |
| precision | 1.0E-6 by default. |
Definition at line 8526 of file linear_algebra.hpp.
| void slip::upper_bidiagonal_solve | ( | RandomAccessIterator1 | diag_first, |
| RandomAccessIterator1 | diag_last, | ||
| RandomAccessIterator1 | up_diag_first, | ||
| RandomAccessIterator1 | up_diag_last, | ||
| RandomAccessIterator2 | X_first, | ||
| RandomAccessIterator2 | X_last, | ||
| RandomAccessIterator3 | B_first, | ||
| RandomAccessIterator3 | B_last, | ||
| typename slip::lin_alg_traits< typename std::iterator_traits< RandomAccessIterator1 >::value_type >::value_type | precision = typename slip::lin_alg_traits<typename std::iterator_traits<RandomAccessIterator1>::value_type>::value_type(1.0E-6) |
||
| ) |
solve Ax = B with A upper bidiagonal
![\[ \left( \begin{array}{ccccc} du_1 & uu_1&0&\cdots&0\\ 0 & \ddots & \ddots&\ddots&\vdots\\ \vdots&\ddots&\ddots&\ddots&0\\ \vdots&&\ddots&\ddots&uu_{n-1}\\ 0&\cdots&\cdots&0&du_{n}\\ \end{array}\right) \left( \begin{array}{c} x_{1}\\ x_{2}\\ \vdots\\ x_n\\ \end{array}\right) = \left( \begin{array}{c} b_{1}\\ b_{2}\\ \vdots\\ b_n\\ \end{array}\right) \]](../../form_107.png)
| diag_first | RandomAccessIterator to the first element of thediagonal. |
| diag_last | RandomAccessIterator to one-past-the-end element of the diagonal. |
| up_diag_first | RandomAccessIterator to the first element of the upper diagonal. |
| up_diag_last | RandomAccessIterator to one-past-the-end element of the upper diagonal. |
| X_first | RandomAccessIterator to the begenning of the result range. |
| X_last | RandomAccessIterator to one-past-the-end of the result range. |
| B_first | RandomAccessIterator to the begenning of the B range. |
| B_last | RandomAccessIterator to one-past-the-end of the B range. |
| precision | 1.0E-6 by default. |
Definition at line 8360 of file linear_algebra.hpp.
|
inline |
Invert an upper triangular Matrix
![\[ \left( \begin{array}{cccc} u_{1,1} & u_{1,2}&\cdots&u_{1,n}\\ 0 & u_{2,2} & \ddots&\vdots\\ \vdots&\ddots&\ddots&u_{n-1,n}\\ 0&\cdots&0&u_{n,n}\\ \end{array}\right)^{-1} \]](../../form_90.png)
.
| A_up | 2D iterator corresponding to the upper_left element of the matrix A |
| A_bot | 2D iterator corresponding to one past-the-end bottom_right of the matrix A |
| Ainv_up | 2D iterator corresponding to the upper_left element of the inverse matrix. |
| Ainv_bot | 2D iterator corresponding to one past-the-end bottom_right of the inverse matrix. |
| precision | 1.0E-6 by default. |
Definition at line 5895 of file linear_algebra.hpp.
|
inline |
Invert an upper triangular Matrix
![\[ \left( \begin{array}{cccc} u_{1,1} & u_{1,2}&\cdots&u_{1,n}\\ 0 & u_{2,2} & \ddots&\vdots\\ \vdots&\ddots&\ddots&u_{n-1,n}\\ 0&\cdots&0&u_{n,n}\\ \end{array}\right)^{-1} \]](../../form_90.png)
.
| A | The matrix to invert. |
| Ainv | The inverted matrix. |
| precision | 1.0E-6 by default. |
Definition at line 5970 of file linear_algebra.hpp.
|
inline |
Solve the linear system U*X=B when U is upper triangular
![\[ \left( \begin{array}{cccc} u_{1,1} & u_{1,2}&\cdots&u_{1,n}\\ 0 & u_{2,2} & \ddots&\vdots\\ \vdots&\ddots&\ddots&u_{n-1,n}\\ 0&\cdots&0&u_{n,n}\\ \end{array}\right) \left( \begin{array}{c} x_{1}\\ x_{2}\\ \vdots\\ x_{n}\\ \end{array}\right) = \left( \begin{array}{c} b_{1}\\ b_{2}\\ \vdots\\ b_{n}\\ \end{array}\right) \]](../../form_89.png)
.
| U_up | 2D iterator corresponding to the upper_left element of the matrix U |
| U_bot | 2D iterator corresponding to one past-the-end bottom_right of the matrix U |
| X_first | RandomAccessIterator point to the first element of X. |
| X_last | RandomAccessIterator point one-past-the-end element of X. |
| B_first | RandomAccessIterator point to the first element of B. |
| B_last | RandomAccessIterator to one-past-the-end element of B. |
| precision |
Definition at line 5722 of file linear_algebra.hpp.
|
inline |
Solve the linear system U*X=B when U is upper triangular
![\[ \left( \begin{array}{cccc} u_{1,1} & u_{1,2}&\cdots&u_{1,n}\\ 0 & u_{2,2} & \ddots&\vdots\\ \vdots&\ddots&\ddots&u_{n-1,n}\\ 0&\cdots&0&u_{n,n}\\ \end{array}\right) \left( \begin{array}{c} x_{1}\\ x_{2}\\ \vdots\\ x_{n}\\ \end{array}\right) = \left( \begin{array}{c} b_{1}\\ b_{2}\\ \vdots\\ b_{n}\\ \end{array}\right) \]](../../form_89.png)
.
| U | 2D container |
| X | 1D container |
| B | 1D container |
| precision |
Definition at line 5836 of file linear_algebra.hpp.
|
inline |
Computes the valid convolution of signal by a 1d-kernel.
| first | A RandomAccessIterator. |
| last | A RandomAccessIterator. |
| kernel_first | A RandomAccessIterator. |
| kernel_last | A RandomAccessIterator. |
| ksize_left | kernel size left to the "center" of the kernel. |
| ksize_right | kernel size right to the "center" of the kernel. |
| result | A RandomAccessIterator. |

Definition at line 134 of file convolution.hpp.
|
inline |
Computes the valid convolution of 2d signal by a 2d-kernel.
| S_up | A RandomAccessIterator2d. |
| S_bot | A RandomAccessIterator2d. |
| kernel_up | A RandomAccessIterator2d. |
| kernel_bot | A RandomAccessIterator2d. |
| ksize_left | Number of elements left to the central point of the mask. |
| ksize_right | Number of elements right to the central point of the mask. |
| ksize_up | Number of elements up to the central point of the mask. |
| ksize_bot | Number of elements bottom to the central point of the mask |
| R_up | A RandomAccessIterator2d. |
| R_bot | A RandomAccessIterator2d. |
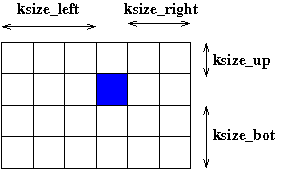
Definition at line 1273 of file convolution.hpp.
|
inline |
Computes the valid convolution of 3d signal by a 3d-kernel.
| S_up | A RandomAccessIterator3d. |
| S_bot | A RandomAccessIterator3d. |
| ksize_front | Number of elements front to the central point of the mask. |
| ksize_back | Number of elements back to the central point of the mask |
| kernel_up | A RandomAccessIterator3d. |
| kernel_bot | A RandomAccessIterator3d. |
| ksize_left | Number of elements left to the central point of the mask. |
| ksize_right | Number of elements right to the central point of the mask. |
| ksize_up | Number of elements up to the central point of the mask. |
| ksize_bot | Number of elements bottom to the central point of the mask. |
| R_up | A RandomAccessIterator3d. |
| R_bot | A RandomAccessIterator3d. |
Definition at line 3434 of file convolution.hpp.
| void slip::var_next | ( | const int | n, |
| const VarT & | prev_mean, | ||
| const VarT & | prev_var, | ||
| const DataT & | xnp1, | ||
| VarT & | next_mean, | ||
| VarT & | next_var | ||
| ) |
Recursive variance algorithm.
| n | Current element index. |
| prev_mean | Previous mean value. |
| xnp1 | Next value of the serie. |
Definition at line 4127 of file statistics.hpp.
|
inline |
Computes the variance of a range
![\[\frac{1}{n}\sum_i (x_i-\overline{x})^2\]](../../form_203.png)
.
| first | An InputIterator. |
| last | An InputIterator. |
| mean | The mean of the container itself. |
Definition at line 535 of file statistics.hpp.
|
inline |
Computes the variance of a range using a predicate
![\[\frac{1}{n}\sum_i (x_i-\overline{x})^2\]](../../form_203.png)
.
| first | An InputIterator. |
| last | An InputIterator. |
| mean | The mean of the range itself using the predicate. |
| pred | a predicate function |
Definition at line 2886 of file statistics.hpp.
|
inline |
Computes the variance of a range over a mask
![\[\frac{1}{n}\sum_i (x_i-\overline{x})^2\]](../../form_203.png)
.
| first | An InputIterator. |
| last | An InputIterator. |
| mask_first | An InputIterator on the mask |
| mean | The mean of the range itself over the mask. |
| value | Mask value. |
Definition at line 1726 of file statistics.hpp.
|
inline |
Computes the multiplication of a vector V by a scalar scal.
| V_first | RandomAccessIterator to the first element of the Vector. |
| V_last | RandomAccessIterator to one-past-the-end element of the vector. |
| scal | A scalar value. |
| result_first | RandomAccessIterator to the first element of the result vector. |
Definition at line 688 of file linear_algebra.hpp.
|
inline |
Computes the multiplication of a vector V by a scalar scal.
| V | The Vector. |
| scal | A scalar value. |
| Result | The result of the scalar multplication. |
Definition at line 733 of file linear_algebra.hpp.
|
inline |
Computes a Householder vector V from a matrix M :
![\[ V = M_{.0} - \alpha \times e_0 \]](../../form_154.png)
with 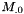 represents the first column of M and
represents the first column of M and
![\[ \alpha = - \frac{ M_{00}}{abs( M_{00})} \times \|M_{.0}\| \]](../../form_156.png)
.
| V | a 1d container for the householder vector |
| M_up | 2D iterator on the upper_left element of M container |
| M_bot | 2D iterator on the bottom_right element of M container |
Definition at line 716 of file linear_algebra_qr.hpp.
|
inline |
Computes the weighted mean value of a range:
![\[\frac{\sum_i w_ix_i}{\sum_i w_i}\]](../../form_199.png)
.
| first | An InputIterator. |
| last | An InputIterator. |
| w_first | An InputIterator to the weight container. |
| w_last | An InputIterator to the weight container. |
Definition at line 352 of file statistics.hpp.
|
inline |
Write a Container1d to an ASCII file.
| first | InputIterator to the first element of the range. |
| last | InputIterator to one past-the-end element of the range. |
| file_path_name | String of the file path name |
Definition at line 2475 of file io_tools.hpp.
|
inline |
Write a Container2d to an ASCII file.
| upper_left | RandomAccessIterator2d. |
| bottom_right | RandomAccessIterator2d. |
| file_path_name | String of the file path name. |
Definition at line 408 of file io_tools.hpp.
|
inline |
Write a Container2d to an ASCII file.
| cont | 2d container to write. |
| file_path_name | String of the file path name. |
Definition at line 475 of file io_tools.hpp.
|
inline |
Write a DenseVector2dField2D to a gnuplot file.
| field | DenseVector2dField2D. |
| file_path_name | String of the file path name |
| precision | Print precision of float values (6 by default). The data format is the following : x y Vx(x,y) Vy(x,y)
x vary first then y. y is written according to the increase order
|
Definition at line 777 of file io_tools.hpp.
|
inline |
Write a DenseVector2dField2D to a gnuplot file handle real regular grid 2d.
| field | DenseVector2dField2D. |
| init_point | Point2d corresponding to the point having the smallest x and y coordinates. |
| step | Point2d corresponding to the steps of the regular grid. |
| file_path_name | String of the file path name |
| precision | Print precision of float values (6 by default). The data format is the following : x y Vx(x,y) Vy(x,y)
x vary first then y. y is written according to the increase order
|
Definition at line 844 of file io_tools.hpp.
|
inline |
Write a Container to an raw file.
| first | InputIterator. |
| last | InputIterator. |
| file_path_name | String of the file path name |
Definition at line 290 of file io_tools.hpp.
|
inline |
Write a Container2d to an ASCII file.
| upper_left | RandomAccessIterator2d. |
| bottom_right | RandomAccessIterator2d. |
| file_path_name | String of the file path name. |
| title | tecplot title string. |
| zone | tecplot zone string. |
| precision | Print precision of float values (6 by default). |
Definition at line 702 of file io_tools.hpp.
|
inline |
Write a DenseVector2dField2D to a tecplot file.
| field | DenseVector2dField2D. |
| file_path_name | String of the file path name |
| title | Title of the data. |
| zone | Name of the zone. |
| precision | Print precision of float values (6 by default). The data format is the following : TITLE= title
VARIABLES= X Y U V
ZONE T= zone, I= rows(), J= cols()
x y U(x,y) V(x,y)
x vary first then y. y is written according to the increase order
|
Definition at line 914 of file io_tools.hpp.
|
inline |
Write a DenseVector2dField2D to a tecplot file handle real regular grid 2d.
| field | DenseVector2dField2D. |
| init_point | Point2d corresponding to the point having the smallest x and y coordinates. |
| step | Point2d corresponding to the steps of the regular grid. |
| file_path_name | String of the file path name |
| title | Title of the data. |
| zone | Name of the zone. The data format is the following : TITLE= title
VARIABLES= X Y U V
ZONE T= zone, I= rows(), J= cols()
x y U(x,y) V(x,y)
x vary first then y. y is written according to the increase order
|
Definition at line 991 of file io_tools.hpp.
|
inline |
Write a DenseVector3dField3D to a tecplot file.
| field | DenseVector3dField3D. |
| file_path_name | String of the file path name |
| title | |
| zone | |
| precision | Print precision of float values (6 by default). The data format is the following : TITLE= title
VARIABLES= X Y Z U V W
ZONE T= zone, I= rows(), J= cols(), K = slices()
x y z U(x,y,z) V(x,y,z) W(x,y,z)
|
Definition at line 1685 of file io_tools.hpp.
|
inline |
Write a DenseVector3dField3D to a tecplot file handle 3d real regular grid.
| field | DenseVector3dField3D. |
| init_point | Point3d corresponding to the point having the smallest x, y and z coordinates. |
| step | Point3d corresponding to the steps of the regular grid. |
| file_path_name | String of the file path name |
| title | |
| zone | |
| precision | Print precision of float values (6 by default). The data format is the following : TITLE= title
VARIABLES= X Y Z U V W
ZONE T= zone, I= rows(), J= cols(), K = slices()
x y z U(x,y,z) V(x,y,z) W(x,y,z)
|
Definition at line 1769 of file io_tools.hpp.
|
inline |
Write a Container3D to a tecplot file.
| container | Container3d. |
| file_path_name | String of the file path name |
| title | The data format is the following : TITLE= title VARIABLES= X Y Z I ZONE T= data, I= rows() J= cols() K= slices() F=POINT x y z I(x,y,z) |
Definition at line 3531 of file io_tools.hpp.
| void slip::write_to_images_tecplot | ( | Container3d & | container, |
| const std::string & | file_path_name, | ||
| const std::string & | title, | ||
| const std::size_t | from, | ||
| const std::size_t | to | ||
| ) |
Write slices of a Container3D to a tecplot file.
| container | Container3d. |
| file_path_name | String of the file path name |
| title | Title of the file. |
| from | Index of the first slice. |
| to | Index of the last slice. |
Definition at line 3597 of file io_tools.hpp.
| const std::string slip::BAD_DIMENSION = "Bad dimension parameter." |
| const std::string slip::CROSSCORRELATION_BAD_ALGO = "Bad crosscorrelation algorithm selection: standard algorithm by default" |
| const std::string slip::FILE_OPEN_ERROR = "Fail to open file: " |
| const std::string slip::FILE_READ_ERROR = "Unable to read the file " |
| const std::string slip::FILE_WRITE_ERROR = "Unable to write into the file " |
| const std::string slip::GRID_INIT_POINT_ERROR = "The init points of the grid are different" |
| const std::string slip::GRID_STEP_ERROR = "The grid steps of the grid are different" |
| const std::string slip::POSITIVE_DEFINITE_MATRIX_ERROR = "This matrix is not positive definite" |
 1.8.6
1.8.6