SLIP  1.4
 All Classes Namespaces Files Functions Variables Typedefs Enumerations Enumerator Friends Macros Groups Pages
Public Types | Public Member Functions | Friends | Related Functions | List of all members
slip::Polynomial< T > Class Template Reference
Group of Containers | 1d Containers | Mathematical containers

Numerical Polynomial class. This container statisfies the RandomAccessContainer concepts of the STL The coefficients of the polynomial 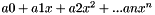$a0 + a1x + a2x^2 +... anx^n $ are ordered as follows : (a0,a1,...,an) More...

#include <Polynomial.hpp>

Public Types

typedef T value_type
 
typedef Polynomial< T > self
 
typedef const Polynomial< T > const_self
 
typedef value_type * pointer
 
typedef const value_type * const_pointer
 
typedef value_type & reference
 
typedef const value_type & const_reference
 
typedef ptrdiff_t difference_type
 
typedef std::size_t size_type
 
typedef pointer iterator
 
typedef const_pointer const_iterator
 
typedef std::reverse_iterator
< iterator > 		reverse_iterator
 
typedef std::reverse_iterator
< const_iterator > 		const_reverse_iterator
 
typedef
std::random_access_iterator_tag 		iterator_category
 

Public Member Functions

std::string name () const
 Returns the name of the class. More...
 
size_type size () const
 Returns the number of elements in the Polynomial. More...
 
size_type degree () const
 Returns the degree of the Polynomial. More...
 
size_type order () const
 Returns the order of the Polynomial. More...
 
size_type max_size () const
 Returns the maximal size (number of elements) in the Polynomial. More...
 
bool empty () const
 Returns true if the Polynomial is empty. (Thus size() == 0) More...
 
void swap (self &M)
 Swaps data with another Polynomial. More...
 
template<typename T>
 Polynomial (const typename Polynomial< T >::size_type n)
 
template<typename T>
 Polynomial (const typename Polynomial< T >::size_type n, const T &val)
 
template<typename T>
 Polynomial (const typename Polynomial< T >::size_type n, const T *val)
 
Constructors & Destructors
 Polynomial ()
 Constructs a Polynomial. More...
 
 Polynomial (const size_type n)
 Constructs a Polynomial. More...
 
 Polynomial (const size_type n, const T &val)
 Constructs a Polynomial initialized by the scalar value val. More...
 
 Polynomial (const size_type n, const T *val)
 Constructs a Polynomial initialized by an array val. More...
 
template<typename InputIterator >
 Polynomial (InputIterator first, InputIterator last)
 Contructs a Polynomial from a range. More...
 
 Polynomial (const self &rhs)
 Constructs a copy of the Polynomial rhs. More...
 
 ~Polynomial ()
 Destructor of the Polynomial. More...
 
iterators
iterator begin ()
 Returns a read/write iterator that points to the first element in the Polynomial. Iteration is done in ordinary element order. More...
 
const_iterator begin () const
 Returns a read-only (constant) iterator that points to the first element in the Polynomial. Iteration is done in ordinary element order. More...
 
iterator end ()
 Returns a read/write iterator that points one past the last element in the Polynomial. Iteration is done in ordinary element order. More...
 
const_iterator end () const
 Returns a read-only (constant) iterator that points one past the last element in the Polynomial. Iteration is done in ordinary element order. More...
 
reverse_iterator rbegin ()
 Returns a read/write reverse iterator that points to the last element in the Polynomial. Iteration is done in reverse element order. More...
 
const_reverse_iterator rbegin () const
 Returns a read-only (constant) reverse iterator that points to the last element in the Polynomial. Iteration is done in reverse element order. More...
 
reverse_iterator rend ()
 Returns a read/write reverse iterator that points to one before the first element in the Polynomial. Iteration is done in reverse element order. More...
 
const_reverse_iterator rend () const
 Returns a read-only (constant) reverse iterator that points to one before the first element in the Polynomial. Iteration is done in reverse element order. More...
 
Assignment operators and methods
self & operator= (const self &rhs)
 Assign a Polynomial. More...
 
self & operator= (const T &val)
 Assigns all the element of the Polynomial by val. More...
 
void fill (const T &value)
 Fills the container range [begin(),begin()+size()) with copies of value. More...
 
void fill (const T *value)
 Fills the container range [begin(),begin()+size()) with a copy of the value array. More...
 
template<typename InputIterator >
void fill (InputIterator first, InputIterator last)
 Fills the container range [begin(),begin()+size()) with a copy of the range [first,last) More...
 
Element access operators
reference operator[] (const size_type i)
 Subscript access to the data contained in the Polynomial. More...
 
const_reference operator[] (const size_type i) const
 Subscript access to the data contained in the Polynomial. More...
 
reference operator() (const size_type i)
 Subscript access to the data contained in the Polynomial. More...
 
const_reference operator() (const size_type i) const
 Subscript access to the data contained in the Polynomial. More...
 
Arithmetic operators
self & operator+= (const T &val)
 Add val to each element of the Polynomial. More...
 
self & operator-= (const T &val)
 
self & operator*= (const T &val)
 
self & operator/= (const T &val)
 
self operator- () const
 
self & operator+= (const self &rhs)
 
self & operator-= (const self &rhs)
 
self & operator*= (const self &rhs)
 
Mathematic operators
self & derivative ()
 Returns the derivative the polynomial. More...
 
self & integral ()
 Returns the integral of the polynomial. The constant of integrationis set to zero. More...
 
double fit (iterator xi_first, iterator xi_last, iterator yi_first, const std::size_t order)
 Return a polynomial P(X) of degree order that minimizes sum_i (P(x(i)) - y(i))^2 to best fit the data in the least squares sense. More...
 
slip::Matrix< T > companion () const
 Computes the companion matrix corresponding to polynomial coefficients. More...
 
slip::Vector< std::complex< T > > roots () const
 Computes the roots of the polynomial. More...
 
T evaluate (const T &x) const
 Returns the evaluation of the polynomial at x. More...
 
template<typename InputIterator , typename OutputIterator >
void multi_evaluate (InputIterator first, InputIterator last, OutputIterator result) const
 Returns the evaluation of the polynomial at each element of the range [first,last). More...
 

Friends

class boost::serialization::access
 
i/o operators
std::ostream & operator<< (std::ostream &out, const self &v)
 Write the Polynomial to the ouput stream. More...
 
Comparison operators
bool operator== (const Polynomial< T > &x, const Polynomial< T > &y)
 Polynomial equality comparison. More...
 
bool operator!= (const Polynomial< T > &x, const Polynomial< T > &y)
 Polynomial inequality comparison. More...
 
bool operator< (const Polynomial< T > &x, const Polynomial< T > &y)
 Less than comparison operator (Polynomial ordering relation) More...
 
bool operator> (const Polynomial< T > &x, const Polynomial< T > &y)
 More than comparison operator. More...
 
bool operator<= (const Polynomial< T > &x, const Polynomial< T > &y)
 Less than equal comparison operator. More...
 
bool operator>= (const Polynomial< T > &x, const Polynomial< T > &y)
 More than equal comparison operator. More...
 

Related Functions

(Note that these are not member functions.)

template<typename T >
Polynomial< T > operator+ (const Polynomial< T > &V1, const Polynomial< T > &V2)
 pointwise addition of two Polynomial More...
 
template<typename T >
Polynomial< T > operator+ (const Polynomial< T > &V, const T &val)
 addition of a scalar to each element of a Polynomial More...
 
template<typename T >
Polynomial< T > operator+ (const T &val, const Polynomial< T > &V)
 addition of a scalar to each element of a Polynomial More...
 
template<typename T >
Polynomial< T > operator- (const Polynomial< T > &V1, const Polynomial< T > &V2)
 pointwise substraction of two Polynomial More...
 
template<typename T >
Polynomial< T > operator- (const Polynomial< T > &V, const T &val)
 substraction of a scalar to each element of a Polynomial More...
 
template<typename T >
Polynomial< T > operator- (const T &val, const Polynomial< T > &V)
 substraction of a scalar to each element of a Polynomial More...
 
template<typename T >
Polynomial< T > operator* (const Polynomial< T > &V1, const Polynomial< T > &V2)
 pointwise multiplication of two Polynomial More...
 
template<typename T >
Polynomial< T > operator* (const Polynomial< T > &V, const T &val)
 multiplication of a scalar to each element of a Polynomial More...
 
template<typename T >
Polynomial< T > operator* (const T &val, const Polynomial< T > &V)
 multiplication of a scalar to each element of a Polynomial More...
 
template<typename T >
Polynomial< T > operator/ (const Polynomial< T > &V, const T &val)
 division of a scalar to each element of a Polynomial More...
 

Detailed Description

template<typename T>
class slip::Polynomial< T >

Numerical Polynomial class. This container statisfies the RandomAccessContainer concepts of the STL The coefficients of the polynomial 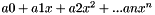$a0 + a1x + a2x^2 +... anx^n $ are ordered as follows : (a0,a1,...,an)

Author
Benoit Tremblais <tremblais_AT_sic.univ-poitiers.fr>
Version
0.0.1
Date
2013/11/15
Since
1.0.0
Parameters
TType of object in the Polynomial
Examples:
example_polynomial.cpp.

Definition at line 104 of file Polynomial.hpp.

Member Typedef Documentation

template<typename T>
typedef const_pointer slip::Polynomial< T >::const_iterator

Definition at line 166 of file Polynomial.hpp.

template<typename T>
typedef const value_type* slip::Polynomial< T >::const_pointer

Definition at line 158 of file Polynomial.hpp.

template<typename T>
typedef const value_type& slip::Polynomial< T >::const_reference

Definition at line 160 of file Polynomial.hpp.

template<typename T>
typedef std::reverse_iterator<const_iterator> slip::Polynomial< T >::const_reverse_iterator

Definition at line 169 of file Polynomial.hpp.

template<typename T>
typedef const Polynomial<T> slip::Polynomial< T >::const_self

Definition at line 155 of file Polynomial.hpp.

template<typename T>
typedef ptrdiff_t slip::Polynomial< T >::difference_type

Definition at line 162 of file Polynomial.hpp.

template<typename T>
typedef pointer slip::Polynomial< T >::iterator

Definition at line 165 of file Polynomial.hpp.

template<typename T>
typedef std::random_access_iterator_tag slip::Polynomial< T >::iterator_category

Definition at line 173 of file Polynomial.hpp.

template<typename T>
typedef value_type* slip::Polynomial< T >::pointer

Definition at line 157 of file Polynomial.hpp.

template<typename T>
typedef value_type& slip::Polynomial< T >::reference

Definition at line 159 of file Polynomial.hpp.

template<typename T>
typedef std::reverse_iterator<iterator> slip::Polynomial< T >::reverse_iterator

Definition at line 168 of file Polynomial.hpp.

template<typename T>
typedef Polynomial<T> slip::Polynomial< T >::self

Definition at line 154 of file Polynomial.hpp.

template<typename T>
typedef std::size_t slip::Polynomial< T >::size_type

Definition at line 163 of file Polynomial.hpp.

template<typename T>
typedef T slip::Polynomial< T >::value_type

Definition at line 153 of file Polynomial.hpp.

Constructor & Destructor Documentation

template<typename T >
slip::Polynomial< T >::Polynomial ( )
inline

Constructs a Polynomial.

Definition at line 836 of file Polynomial.hpp.

template<typename T>
slip::Polynomial< T >::Polynomial ( const size_type  n)

Constructs a Polynomial.

Parameters
nnumber of element in the Polynomial
template<typename T>
slip::Polynomial< T >::Polynomial ( const size_type  n,
const T &  val 
)

Constructs a Polynomial initialized by the scalar value val.

Parameters
nnumber of element in the Polynomial
valinitialization value of the elements
template<typename T>
slip::Polynomial< T >::Polynomial ( const size_type  n,
const T *  val 
)

Constructs a Polynomial initialized by an array val.

Parameters
nnumber of element in the Polynomial
valinitialization array value of the elements
template<typename T>
template<typename InputIterator >
slip::Polynomial< T >::Polynomial ( InputIterator  first,
InputIterator  last 
)
inline

Contructs a Polynomial from a range.

Parameters
firstAn input iterator.
lastAn input iterator.
Precondition
last > first Create a Polynomial consisting of copies of the elements from [first,last).

Definition at line 217 of file Polynomial.hpp.

template<typename T>
slip::Polynomial< T >::Polynomial ( const self &  rhs)
inline

Constructs a copy of the Polynomial rhs.

Definition at line 864 of file Polynomial.hpp.

template<typename T >
slip::Polynomial< T >::~Polynomial ( )
inline

Destructor of the Polynomial.

Definition at line 882 of file Polynomial.hpp.

template<typename T>
template<typename T>
slip::Polynomial< T >::Polynomial ( const typename Polynomial< T >::size_type  n)
inline

Definition at line 842 of file Polynomial.hpp.

template<typename T>
template<typename T>
slip::Polynomial< T >::Polynomial ( const typename Polynomial< T >::size_type  n,
const T &  val 
)
inline

Definition at line 848 of file Polynomial.hpp.

template<typename T>
template<typename T>
slip::Polynomial< T >::Polynomial ( const typename Polynomial< T >::size_type  n,
const T *  val 
)
inline

Definition at line 855 of file Polynomial.hpp.

Member Function Documentation

template<typename T >
Polynomial< T >::iterator slip::Polynomial< T >::begin ( )
inline

Returns a read/write iterator that points to the first element in the Polynomial. Iteration is done in ordinary element order.

Returns
begin iterator value

Definition at line 898 of file Polynomial.hpp.

template<typename T >
Polynomial< T >::const_iterator slip::Polynomial< T >::begin ( ) const
inline

Returns a read-only (constant) iterator that points to the first element in the Polynomial. Iteration is done in ordinary element order.

Returns
const begin iterator value

Definition at line 912 of file Polynomial.hpp.

template<typename T >
slip::Matrix< T > slip::Polynomial< T >::companion ( ) const
inline

Computes the companion matrix corresponding to polynomial coefficients.

Returns
The companion Matrix.
Remarks
The eigen values of the companion matrix are the roots of the polynomial.

Definition at line 1065 of file Polynomial.hpp.

template<typename T >
Polynomial< T >::size_type slip::Polynomial< T >::degree ( ) const
inline

Returns the degree of the Polynomial.

Definition at line 1122 of file Polynomial.hpp.

template<typename T >
Polynomial< T > & slip::Polynomial< T >::derivative ( )
inline

Returns the derivative the polynomial.

Definition at line 1005 of file Polynomial.hpp.

template<typename T >
bool slip::Polynomial< T >::empty ( ) const
inline

Returns true if the Polynomial is empty. (Thus size() == 0)

Definition at line 1145 of file Polynomial.hpp.

template<typename T >
Polynomial< T >::iterator slip::Polynomial< T >::end ( )
inline

Returns a read/write iterator that points one past the last element in the Polynomial. Iteration is done in ordinary element order.

Returns
end iterator value

Definition at line 905 of file Polynomial.hpp.

template<typename T >
Polynomial< T >::const_iterator slip::Polynomial< T >::end ( ) const
inline

Returns a read-only (constant) iterator that points one past the last element in the Polynomial. Iteration is done in ordinary element order.

Returns
const end iterator value

Definition at line 919 of file Polynomial.hpp.

template<typename T>
T slip::Polynomial< T >::evaluate ( const T &  x) const
inline

Returns the evaluation of the polynomial at x.

Parameters
xLocation to be evaluated.

Definition at line 1104 of file Polynomial.hpp.

template<typename T>
void slip::Polynomial< T >::fill ( const T &  value)
inline

Fills the container range [begin(),begin()+size()) with copies of value.

Parameters
valueA reference-to-const of arbitrary type.

Definition at line 349 of file Polynomial.hpp.

template<typename T>
void slip::Polynomial< T >::fill ( const T *  value)
inline

Fills the container range [begin(),begin()+size()) with a copy of the value array.

Parameters
valueA pointer of arbitrary type.

Definition at line 368 of file Polynomial.hpp.

template<typename T>
template<typename InputIterator >
void slip::Polynomial< T >::fill ( InputIterator  first,
InputIterator  last 
)
inline

Fills the container range [begin(),begin()+size()) with a copy of the range [first,last)

Parameters
firstAn input iterator.
lastAn input iterator.

Definition at line 383 of file Polynomial.hpp.

template<typename T>
double slip::Polynomial< T >::fit ( iterator  xi_first,
iterator  xi_last,
iterator  yi_first,
const std::size_t  order 
)
inline

Return a polynomial P(X) of degree order that minimizes sum_i (P(x(i)) - y(i))^2 to best fit the data in the least squares sense.

Parameters
xi_firstconst_iterator on the xi first value
xi_lastconst_iterator on the xi past-the-end value
yi_firstconst_iterator on the yi first value
orderOrder or degree of the polynomial that fit the data.
Returns
chi_square value
Example:
slip::Polynomial<double> P6;
slip::Vector<double> xi(4);
xi[0] = 0.0;
xi[1] = 1.0;
xi[2] = 4.0;
xi[3] = 5.0;
slip::Vector<double> yi(4);
yi[0] = 2.0;
yi[1] = 7.0;
yi[2] = 22.0;
yi[3] = 27.0;
double err_P6 = P6.fit(xi.begin(),xi.end(),yi.begin(),2);
std::cout<<P6<<std::endl;
std::cout<<"error = "<<err_P6<<std::endl;

Definition at line 1044 of file Polynomial.hpp.

template<typename T >
Polynomial< T > & slip::Polynomial< T >::integral ( )
inline

Returns the integral of the polynomial. The constant of integrationis set to zero.

Definition at line 1029 of file Polynomial.hpp.

template<typename T >
Polynomial< T >::size_type slip::Polynomial< T >::max_size ( ) const
inline

Returns the maximal size (number of elements) in the Polynomial.

Definition at line 1138 of file Polynomial.hpp.

template<typename T>
template<typename InputIterator , typename OutputIterator >
void slip::Polynomial< T >::multi_evaluate ( InputIterator  first,
InputIterator  last,
OutputIterator  result 
) const
inline

Returns the evaluation of the polynomial at each element of the range [first,last).

Parameters
firstInputIterator.
lastInputIterator.
resultOutputIterator.
Precondition
The two ranges must have the same size.

Definition at line 621 of file Polynomial.hpp.

template<typename T >
std::string slip::Polynomial< T >::name ( ) const
inline

Returns the name of the class.

Definition at line 1113 of file Polynomial.hpp.

template<typename T>
reference slip::Polynomial< T >::operator() ( const size_type  i)

Subscript access to the data contained in the Polynomial.

Parameters
iThe index of the row for which the data should be accessed.
Returns
Read/write reference to data.
Precondition
i < size()

This operator allows for easy, array-style, data access. Note that data access with this operator is unchecked and out_of_range lookups are not defined.

template<typename T>
const_reference slip::Polynomial< T >::operator() ( const size_type  i) const

Subscript access to the data contained in the Polynomial.

Parameters
iThe index of the row for which the data should be accessed.
Returns
Read_only (constant) reference to data.
Precondition
i < size()

This operator allows for easy, array-style, data access. Note that data access with this operator is unchecked and out_of_range lookups are not defined.

template<typename T>
Polynomial< T > & slip::Polynomial< T >::operator*= ( const T &  val)
inline

Definition at line 1177 of file Polynomial.hpp.

template<typename T>
Polynomial< T > & slip::Polynomial< T >::operator*= ( const self &  rhs)
inline

Definition at line 1252 of file Polynomial.hpp.

template<typename T>
Polynomial< T > & slip::Polynomial< T >::operator+= ( const T &  val)
inline

Add val to each element of the Polynomial.

Parameters
valvalue
Returns
reference to the resulting Polynomial

Definition at line 1157 of file Polynomial.hpp.

template<typename T>
Polynomial< T > & slip::Polynomial< T >::operator+= ( const self &  rhs)
inline

Definition at line 1205 of file Polynomial.hpp.

template<typename T >
Polynomial< T > slip::Polynomial< T >::operator- ( ) const
inline

Definition at line 1196 of file Polynomial.hpp.

template<typename T>
Polynomial< T > & slip::Polynomial< T >::operator-= ( const T &  val)
inline

Definition at line 1167 of file Polynomial.hpp.

template<typename T>
Polynomial< T > & slip::Polynomial< T >::operator-= ( const self &  rhs)
inline

Definition at line 1228 of file Polynomial.hpp.

template<typename T>
Polynomial< T > & slip::Polynomial< T >::operator/= ( const T &  val)
inline

Definition at line 1186 of file Polynomial.hpp.

template<typename T >
Polynomial< T > & slip::Polynomial< T >::operator= ( const self &  rhs)
inline

Assign a Polynomial.

Assign elements of Polynomial in rhs

Parameters
rhsPolynomial to get the values from.
Returns

Definition at line 870 of file Polynomial.hpp.

template<typename T>
Polynomial< T > & slip::Polynomial< T >::operator= ( const T &  val)
inline

Assigns all the element of the Polynomial by val.

Parameters
valaffectation value
Returns
reference to corresponding Polynomial

Definition at line 889 of file Polynomial.hpp.

template<typename T>
reference slip::Polynomial< T >::operator[] ( const size_type  i)

Subscript access to the data contained in the Polynomial.

Parameters
iThe index of the row for which the data should be accessed.
Returns
Read/write reference to data.
Precondition
i < size()

This operator allows for easy, array-style, data access. Note that data access with this operator is unchecked and out_of_range lookups are not defined.

template<typename T>
const_reference slip::Polynomial< T >::operator[] ( const size_type  i) const

Subscript access to the data contained in the Polynomial.

Parameters
iThe index of the row for which the data should be accessed.
Returns
Read_only (constant) reference to data.
Precondition
i < size()

This operator allows for easy, array-style, data access. Note that data access with this operator is unchecked and out_of_range lookups are not defined.

template<typename T >
Polynomial< T >::size_type slip::Polynomial< T >::order ( ) const
inline

Returns the order of the Polynomial.

Remarks
Same value as degree

Definition at line 1131 of file Polynomial.hpp.

template<typename T >
Polynomial< T >::reverse_iterator slip::Polynomial< T >::rbegin ( )
inline

Returns a read/write reverse iterator that points to the last element in the Polynomial. Iteration is done in reverse element order.

Returns
reverse begin iterator value

Definition at line 927 of file Polynomial.hpp.

template<typename T >
Polynomial< T >::const_reverse_iterator slip::Polynomial< T >::rbegin ( ) const
inline

Returns a read-only (constant) reverse iterator that points to the last element in the Polynomial. Iteration is done in reverse element order.

Returns
const reverse begin iterator value

Definition at line 941 of file Polynomial.hpp.

template<typename T >
Polynomial< T >::reverse_iterator slip::Polynomial< T >::rend ( )
inline

Returns a read/write reverse iterator that points to one before the first element in the Polynomial. Iteration is done in reverse element order.

Returns
reverse end iterator value

Definition at line 934 of file Polynomial.hpp.

template<typename T >
Polynomial< T >::const_reverse_iterator slip::Polynomial< T >::rend ( ) const
inline

Returns a read-only (constant) reverse iterator that points to one before the first element in the Polynomial. Iteration is done in reverse element order.

Returns
const reverse end iterator value

Definition at line 948 of file Polynomial.hpp.

template<typename T >
slip::Vector< std::complex< T > > slip::Polynomial< T >::roots ( ) const
inline

Computes the roots of the polynomial.

Returns
The roots.
Remarks
The eigen values of the companion matrix are the roots of the polynomial.

Definition at line 1093 of file Polynomial.hpp.

template<typename T >
Polynomial< T >::size_type slip::Polynomial< T >::size ( ) const
inline

Returns the number of elements in the Polynomial.

Definition at line 1117 of file Polynomial.hpp.

template<typename T >
void slip::Polynomial< T >::swap ( self &  M)
inline

Swaps data with another Polynomial.

Parameters
MA Polynomial of the same element type

Definition at line 1149 of file Polynomial.hpp.

Friends And Related Function Documentation

template<typename T>
friend class boost::serialization::access
friend

Definition at line 698 of file Polynomial.hpp.

template<typename T>
bool operator!= ( const Polynomial< T > &  x,
const Polynomial< T > &  y 
)
friend

Polynomial inequality comparison.

Parameters
xA Polynomial
yA Polynomial of the same type of x
Returns
true if !(x == y)

Definition at line 1430 of file Polynomial.hpp.

template<typename T >
Polynomial< T > operator* ( const Polynomial< T > &  V1,
const Polynomial< T > &  V2 
)
related

pointwise multiplication of two Polynomial

Parameters
V1The first Polynomial
V2The second Polynomial
Precondition
V1.size() == V2.size()
Returns
resulting Polynomial

Definition at line 1368 of file Polynomial.hpp.

template<typename T >
Polynomial< T > operator* ( const Polynomial< T > &  V,
const T &  val 
)
related

multiplication of a scalar to each element of a Polynomial

Parameters
VThe Polynomial
valThe scalar
Returns
resulting Polynomial

Definition at line 1390 of file Polynomial.hpp.

template<typename T >
Polynomial< T > operator* ( const T &  val,
const Polynomial< T > &  V 
)
related

multiplication of a scalar to each element of a Polynomial

Parameters
valThe scalar
VThe Polynomial
Returns
resulting Polynomial

Definition at line 1400 of file Polynomial.hpp.

template<typename T >
Polynomial< T > operator+ ( const Polynomial< T > &  V1,
const Polynomial< T > &  V2 
)
related

pointwise addition of two Polynomial

Parameters
V1The first Polynomial
V2The second Polynomial
Precondition
V1.size() == V2.size()
Returns
resulting Polynomial

Definition at line 1312 of file Polynomial.hpp.

template<typename T >
Polynomial< T > operator+ ( const Polynomial< T > &  V,
const T &  val 
)
related

addition of a scalar to each element of a Polynomial

Parameters
VThe Polynomial
valThe scalar
Returns
resulting Polynomial

Definition at line 1322 of file Polynomial.hpp.

template<typename T >
Polynomial< T > operator+ ( const T &  val,
const Polynomial< T > &  V 
)
related

addition of a scalar to each element of a Polynomial

Parameters
valThe scalar
VThe Polynomial
Returns
resulting Polynomial

Definition at line 1332 of file Polynomial.hpp.

template<typename T >
Polynomial< T > operator- ( const Polynomial< T > &  V1,
const Polynomial< T > &  V2 
)
related

pointwise substraction of two Polynomial

Parameters
V1The first Polynomial
V2The second Polynomial
Precondition
V1.size() == V2.size()
Returns
resulting Polynomial

Definition at line 1340 of file Polynomial.hpp.

template<typename T >
Polynomial< T > operator- ( const Polynomial< T > &  V,
const T &  val 
)
related

substraction of a scalar to each element of a Polynomial

Parameters
VThe Polynomial
valThe scalar
Returns
resulting Polynomial

Definition at line 1350 of file Polynomial.hpp.

template<typename T >
Polynomial< T > operator- ( const T &  val,
const Polynomial< T > &  V 
)
related

substraction of a scalar to each element of a Polynomial

Parameters
valThe scalar
VThe Polynomial
Returns
resulting Polynomial

Definition at line 1360 of file Polynomial.hpp.

template<typename T >
Polynomial< T > operator/ ( const Polynomial< T > &  V,
const T &  val 
)
related

division of a scalar to each element of a Polynomial

Parameters
VThe Polynomial
valThe scalar
Returns
resulting Polynomial

Definition at line 1410 of file Polynomial.hpp.

template<typename T>
bool operator< ( const Polynomial< T > &  x,
const Polynomial< T > &  y 
)
friend

Less than comparison operator (Polynomial ordering relation)

Parameters
xA Polynomial
yA Polynomial of the same type of x
Returns
true iff x is lexicographically less than y

Definition at line 1440 of file Polynomial.hpp.

template<typename T>
std::ostream& operator<< ( std::ostream &  out,
const self &  v 
)
friend

Write the Polynomial to the ouput stream.

Parameters
outoutput std:ostream
vPolynomial to write to the output stream

Definition at line 956 of file Polynomial.hpp.

template<typename T>
bool operator<= ( const Polynomial< T > &  x,
const Polynomial< T > &  y 
)
friend

Less than equal comparison operator.

Parameters
xA Polynomial
yA Polynomial of the same type of x
Returns
true iff !(y > x)

Definition at line 1456 of file Polynomial.hpp.

template<typename T>
bool operator== ( const Polynomial< T > &  x,
const Polynomial< T > &  y 
)
friend

Polynomial equality comparison.

Parameters
xA Polynomial
yA Polynomial of the same type of x
Returns
true iff the size and the elements of the Arrays are equal

Definition at line 1422 of file Polynomial.hpp.

template<typename T>
bool operator> ( const Polynomial< T > &  x,
const Polynomial< T > &  y 
)
friend

More than comparison operator.

Parameters
xA Polynomial
yA Polynomial of the same type of x
Returns
true iff y > x

Definition at line 1448 of file Polynomial.hpp.

template<typename T>
bool operator>= ( const Polynomial< T > &  x,
const Polynomial< T > &  y 
)
friend

More than equal comparison operator.

Parameters
xA Polynomial
yA Polynomial of the same type of x
Returns
true iff !(x < y)

Definition at line 1464 of file Polynomial.hpp.

The documentation for this class was generated from the following file:
Generated on Tue Sep 30 2014 10:06:37 for SLIP by   doxygen 1.8.6