|
SLIP
1.4
|
|
SLIP
1.4
|
Provides common linear algebra algorithms. More...
#include <iterator>#include <algorithm>#include <numeric>#include <cassert>#include <cmath>#include <limits>#include <iostream>#include <complex>#include <stdexcept>#include "complex_cast.hpp"#include "Array2d.hpp"#include "Array.hpp"#include "macros.hpp"#include "arithmetic_op.hpp"#include "linear_algebra_traits.hpp"#include "error.hpp"#include "apply.hpp"#include "norms.hpp"
Go to the source code of this file.
Classes | |
| struct | slip::saxpy< _F, _S, _RT, _AT > |
Computes the saxpy ("scalar a x plus b") operation: ( 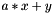 ) between two values. More... ) between two values. More... | |
| struct | slip::z1conjz2< _Tp > |
Computes the complex operation: ( 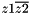 ) between two complex values z1 and z2. More... ) between two complex values z1 and z2. More... | |
| struct | slip::conjz1z2< _Tp > |
Computes the complex operation: ( 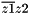 ) between two complex values z1 and z2. More... ) between two complex values z1 and z2. More... | |
Namespaces | |
| slip | |
| This namespace corresponds to the kernel of the Simple Library on Image Processing (SLIP). That is to say that it contains the data structures and the algorithms needed by these data strucutres. | |
Functions | |
Matrix vector algorithms | |
| template<class RandomAccessIterator2d , class RandomAccessIterator1 , class RandomAccessIterator2 > | |
| void | slip::matrix_vector_multiplies (RandomAccessIterator2d M_upper_left, RandomAccessIterator2d M_bottom_right, RandomAccessIterator1 first1, RandomAccessIterator1 last1, RandomAccessIterator2 result_first, RandomAccessIterator2 result_last) |
| Computes the multiplication of a Matrix and a Vector: Result=MV. More... | |
| template<typename AT , typename RandomAccessIterator1 , typename RandomAccessIterator2 > | |
| void | slip::aXpY (const AT &a, RandomAccessIterator1 first1, RandomAccessIterator1 last1, RandomAccessIterator2 first2) |
| Computes the saxpy ("scalar a x plus b") for each element of two ranges x and y. More... | |
| template<typename RandomAccessIterator1 , typename T , typename RandomAccessIterator2 > | |
| void | slip::vector_scalar_multiplies (RandomAccessIterator1 V_first, RandomAccessIterator1 V_last, const T &scal, RandomAccessIterator2 result_first) |
| Computes the multiplication of a vector V by a scalar scal. More... | |
| template<typename Vector1 , typename T , typename Vector2 > | |
| void | slip::vector_scalar_multiplies (const Vector1 &V, const T &scal, Vector2 &Result) |
| Computes the multiplication of a vector V by a scalar scal. More... | |
| template<typename RandomAccessIterator1 , typename T , typename RandomAccessIterator2 > | |
| void | slip::conj_vector_scalar_multiplies (RandomAccessIterator1 V_first, RandomAccessIterator1 V_last, const T &scal, RandomAccessIterator2 result_first) |
Computes the multiplication of a vector 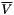 by a scalar scal. More... by a scalar scal. More... | |
| template<typename Vector1 , typename T , typename Vector2 > | |
| void | slip::conj_vector_scalar_multiplies (const Vector1 &V, const T &scal, Vector2 &Result) |
Computes the multiplication of a vector 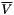 by a scalar scal. More... by a scalar scal. More... | |
| template<class RandomAccessIterator2d1 , class T , class RandomAccessIterator2d2 > | |
| void | slip::matrix_scalar_multiplies (RandomAccessIterator2d1 M_upper_left, RandomAccessIterator2d1 M_bottom_right, const T &scal, RandomAccessIterator2d2 R_upper_left, RandomAccessIterator2d2 R_bottom_right) |
| Computes the multiplication of a Matrix by a scalar R = M*scal. More... | |
| template<class Matrix1 , class T , class Matrix2 > | |
| void | slip::matrix_scalar_multiplies (const Matrix1 &M, const T &scal, Matrix2 &R) |
| Computes the multiplication of a Matrix by a scalar R = M*scal. More... | |
| template<class Matrix , class Vector1 , class Vector2 > | |
| void | slip::matrix_vector_multiplies (const Matrix &M, const Vector1 &V, Vector2 &Result) |
| Computes the multiplication of a Matrix and a Vector: Result=MV. More... | |
| template<class RandomAccessIterator2d , class RandomAccessIterator1 , class RandomAccessIterator2 > | |
| void | slip::hvector_matrix_multiplies (RandomAccessIterator1 V_first, RandomAccessIterator1 V_last, RandomAccessIterator2d M_up, RandomAccessIterator2d M_bot, RandomAccessIterator2 result_first, RandomAccessIterator2 result_last) |
| Computes the hermitian left multiplication:
. More... | |
| template<class Vector1 , class Matrix , class Vector2 > | |
| void | slip::hvector_matrix_multiplies (const Vector1 &V, const Matrix &M, Vector2 &R) |
| Computes the hermitian left multiplication:
. More... | |
| template<class RandomAccessIterator2d , class RandomAccessIterator1 , class RandomAccessIterator2 > | |
| void | slip::tvector_matrix_multiplies (RandomAccessIterator1 V_first, RandomAccessIterator1 V_last, RandomAccessIterator2d M_up, RandomAccessIterator2d M_bot, RandomAccessIterator2 result_first, RandomAccessIterator2 result_last) |
| Computes the transpose left multiplication:
. More... | |
| template<class Vector1 , class Matrix , class Vector2 > | |
| void | slip::tvector_matrix_multiplies (const Vector1 &V, const Matrix &M, Vector2 &R) |
| Computes the transpose left multiplication:
. More... | |
| template<class RandomAccessIterator2d1 , class RandomAccessIterator2d2 , class RandomAccessIterator2d3 > | |
| void | slip::hmatrix_matrix_multiplies (RandomAccessIterator2d1 M1_up, RandomAccessIterator2d1 M1_bot, RandomAccessIterator2d2 M2_up, RandomAccessIterator2d2 M2_bot, RandomAccessIterator2d3 result_up, RandomAccessIterator2d3 result_bot) |
| Computes the hermitian left multiplication of a matrix:
. More... | |
| template<class Matrix1 , class Matrix2 , class Matrix3 > | |
| void | slip::hmatrix_matrix_multiplies (const Matrix1 &M1, const Matrix2 &M2, Matrix3 &Result) |
| Computes the hermitian left multiplication of a matrix:
. More... | |
| template<class RandomAccessIterator2d , class RandomAccessIterator1 , class RandomAccessIterator2 > | |
| void | slip::hmatrix_vector_multiplies (RandomAccessIterator2d M_up, RandomAccessIterator2d M_bot, RandomAccessIterator1 V_first, RandomAccessIterator1 V_last, RandomAccessIterator2 R_first, RandomAccessIterator2 R_last) |
| Computes the hermitian matrix left multiplication of a vector:
. More... | |
| template<class Matrix , class Vector1 , class Vector2 > | |
| void | slip::hmatrix_vector_multiplies (const Matrix &M, const Vector1 &V, Vector2 &R) |
| Computes the hermitian matrix left multiplication of a vector:
. More... | |
| template<typename RandomAccessIterator2d , typename RandomAccessIterator1 , typename RandomAccessIterator2 > | |
| void | slip::gen_matrix_vector_multiplies (RandomAccessIterator2d M_up, RandomAccessIterator2d M_bot, RandomAccessIterator1 V_first, RandomAccessIterator1 V_last, RandomAccessIterator2 Y_first, RandomAccessIterator2 Y_last) |
| Computes the generalised multiplication of a Matrix and a Vector: computes the update
. More... | |
| template<class Matrix , class Vector1 , class Vector2 > | |
| void | slip::gen_matrix_vector_multiplies (const Matrix &M, const Vector1 &V, Vector2 &Y) |
| Computes the generalised multiplication of a Matrix and a Vector: computes the update
. More... | |
| template<typename MatrixIterator1 , typename MatrixIterator2 , typename MatrixIterator3 > | |
| void | slip::matrix_matrix_multiplies (MatrixIterator1 M1_up, MatrixIterator1 M1_bot, MatrixIterator2 M2_up, MatrixIterator2 M2_bot, MatrixIterator3 R_up, MatrixIterator3 R_bot) |
| Computes the matrix matrix multiplication of 2 2d ranges. More... | |
| template<class Matrix1 , class Matrix2 , class Matrix3 > | |
| void | slip::matrix_matrix_multiplies (const Matrix1 &M1, const Matrix2 &M2, Matrix3 &Result) |
| Computes the multiplication of a two Matrix. More... | |
| template<typename RandomAccessIterator2d1 , typename RandomAccessIterator2d2 , typename RandomAccessIterator2d3 > | |
| void | slip::gen_matrix_matrix_multiplies (RandomAccessIterator2d1 A_up, RandomAccessIterator2d1 A_bot, RandomAccessIterator2d2 B_up, RandomAccessIterator2d2 B_bot, RandomAccessIterator2d3 C_up, RandomAccessIterator2d3 C_bot) |
| Computes the generalized multiplication of a two Matrix:
. More... | |
| template<class Matrix1 , class Matrix2 , class Matrix3 > | |
| void | slip::gen_matrix_matrix_multiplies (const Matrix1 &A, const Matrix2 &B, Matrix3 &C) |
| Computes the generalized multiplication of a two Matrix:
. More... | |
| template<class Matrix1 , class Matrix2 , class Matrix3 > | |
| void | slip::multiplies (const Matrix1 &M1, const std::size_t nr1, const std::size_t nc1, const Matrix2 &M2, const std::size_t nr2, const std::size_t nc2, Matrix3 &Result, const std::size_t nr3, const std::size_t nc3) |
| Computes the multiplication of two Matrix. More... | |
| template<class Matrix1 , class Matrix2 , class Matrix3 > | |
| void | slip::multiplies (const Matrix1 &M, const std::size_t nrm, const std::size_t ncm, const Matrix2 &V, const std::size_t nrv, Matrix3 &Result, const std::size_t nrr) |
| Computes the multiplication of a Matrix with a Vector. More... | |
| template<class Matrix1 , class Matrix2 , class Matrix3 > | |
| void | slip::multiplies (const Matrix1 &M1, const Matrix2 &M2, Matrix3 &Result) |
| Computes the multiplication of two Matrix. More... | |
| template<typename MatrixIterator1 , typename MatrixIterator2 , typename MatrixIterator3 > | |
| void | slip::multiplies (MatrixIterator1 A1_up, MatrixIterator1 A1_bot, MatrixIterator2 A2_up, MatrixIterator2 A2_bot, MatrixIterator3 Res_up, MatrixIterator3 Res_bot) |
Computes the multiplication of two matrices 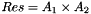 . More... . More... | |
| template<class RandomAccessIterator2d1 , class RandomAccessIterator2d2 > | |
| void | slip::matrix_matrixt_multiplies (RandomAccessIterator2d1 M1_up, RandomAccessIterator2d1 M1_bot, RandomAccessIterator2d2 Res_up, RandomAccessIterator2d2 Res_bot) |
Computes the multiplication of a matrix with its transposate A^T 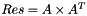 . More... . More... | |
| template<class Matrix1 , class Matrix2 > | |
| void | slip::matrix_matrixt_multiplies (const Matrix1 &M1, Matrix2 &result) |
Computes the multiplication of A and its transposate AT 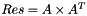 . More... . More... | |
| template<class RandomAccessIterator2d1 , class T , class RandomAccessIterator2d2 > | |
| void | slip::matrix_shift (RandomAccessIterator2d1 M_upper_left, RandomAccessIterator2d1 M_bottom_right, const T &lambda, RandomAccessIterator2d2 R_upper_left, RandomAccessIterator2d2 R_bottom_right) |
| Computes
with In the identity matrix. More... | |
| template<class RandomAccessIterator2d1 , class T > | |
| void | slip::matrix_shift (RandomAccessIterator2d1 M_upper_left, RandomAccessIterator2d1 M_bottom_right, const T &lambda) |
| Computes
with In the identity matrix. More... | |
| template<class Matrix1 , class T , class Matrix2 > | |
| void | slip::matrix_shift (const Matrix1 &A, const T &lambda, Matrix2 &R) |
| Computes
with In the identity matrix. More... | |
| template<class Matrix , class T > | |
| void | slip::matrix_shift (Matrix &A, const T &lambda) |
| Computes
with In the identity matrix. More... | |
| template<typename RandomAccessIterator2d1 , typename T , typename RandomAccessIterator1 , typename RandomAccessIterator2 > | |
| void | slip::rank1_update (RandomAccessIterator2d1 A_up, RandomAccessIterator2d1 A_bot, const T &alpha, RandomAccessIterator1 X_first, RandomAccessIterator1 X_last, RandomAccessIterator2 Y_first, RandomAccessIterator2 Y_last) |
| Computes
. More... | |
| template<typename Matrix , typename T , typename Vector1 , typename Vector2 > | |
| void | slip::rank1_update (Matrix &A, const T &alpha, const Vector1 &X, const Vector2 &Y) |
| Computes
. More... | |
| template<typename Iterator1 , typename Iterator2 , typename U > | |
| void | slip::reduction (Iterator1 seq1_beg, Iterator1 seq1_end, Iterator2 seq2_beg, U u) |
| Add u times the second sequence to the first one: seq1 = seq1 + u * seq2. More... | |
| template<class Matrix1 , class Matrix2 > | |
| void | slip::hermitian_transpose (const Matrix1 &M, Matrix2 &TM) |
Computes the hermitian transpose of a matrix 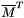 which is the transpose of the conjugate. More... which is the transpose of the conjugate. More... | |
| template<class Matrix1 , class Matrix2 > | |
| void | slip::transpose (const Matrix1 &M, const std::size_t nr1, const std::size_t nc1, Matrix2 &TM, const std::size_t nr2, const std::size_t nc2) |
Computes the transpose of a matrix 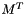 . More... . More... | |
| template<class Matrix1 , class Matrix2 > | |
| void | slip::transpose (const Matrix1 &M, Matrix2 &TM) |
Computes the transpose of a matrix 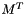 . More... . More... | |
| template<class Matrix1 , class Matrix2 > | |
| void | slip::conj (const Matrix1 &M, Matrix2 &CM) |
Computes the conjugate of a matrix 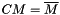 . More... . More... | |
| template<class Matrix1 , class Matrix2 > | |
| void | slip::real (const Matrix1 &C, Matrix2 &R) |
Extract the real Matrix of a complex Matrix. 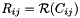 . More... . More... | |
| template<class Matrix1 , class Matrix2 > | |
| void | slip::imag (const Matrix1 &C, Matrix2 &I) |
Extract the imaginary Matrix of a complex Matrix. 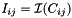 . More... . More... | |
| template<typename VectorIterator1 , typename VectorIterator2 , typename MatrixIterator > | |
| void | slip::outer_product (VectorIterator1 V_begin, VectorIterator1 V_end, VectorIterator2 W_begin, VectorIterator2 W_end, MatrixIterator R_up, MatrixIterator R_bot) |
| Computes the hermitian outer product of the vector V and the transpose of the conjugate of the vector W:
. More... | |
| template<class RandomAccessIterator1 , class RandomAccessIterator2 , class RandomAccessIterator2d > | |
| void | slip::rank1_tensorial_product (RandomAccessIterator1 base1_first, RandomAccessIterator1 base1_end, RandomAccessIterator2 base2_first, RandomAccessIterator2 base2_end, RandomAccessIterator2d matrix_upper_left, RandomAccessIterator2d matrix_bottom_right) |
Computes the tensorial product of two rank one tensors 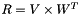 it provides a rank2 tensor (Container2d) of size (MxN) if M and N are respectivly the size of V and W. More... it provides a rank2 tensor (Container2d) of size (MxN) if M and N are respectivly the size of V and W. More... | |
| template<class RandomAccessIterator1 , class RandomAccessIterator2 , class RandomAccessIterator3 , class RandomAccessIterator3d > | |
| void | slip::rank1_tensorial_product (RandomAccessIterator1 base1_first, RandomAccessIterator1 base1_end, RandomAccessIterator2 base2_first, RandomAccessIterator2 base2_end, RandomAccessIterator3 base3_first, RandomAccessIterator3 base3_end, RandomAccessIterator3d base_front_upper_left, RandomAccessIterator3d base_back_bottom_right) |
| Computes the tensorial product of three rank one tensors it provides a rank3 tensor (Container3d) of size (PxMxN) if P, M and N are respectivly the size of V, W and X. More... | |
Inner-poduct algorithms | |
| template<typename RandomAccessIterator1 , typename RandomAccessIterator2 > | |
| std::iterator_traits < RandomAccessIterator1 > ::value_type | slip::hermitian_inner_product (RandomAccessIterator1 first1, RandomAccessIterator1 last1, RandomAccessIterator2 first2, typename std::iterator_traits< RandomAccessIterator1 >::value_type init) |
| Computes the hermitian inner-product of two ranges X and Y:
. More... | |
| template<typename RandomAccessIterator1 , typename RandomAccessIterator2 > | |
| std::iterator_traits < RandomAccessIterator1 > ::value_type | slip::inner_product (RandomAccessIterator1 first1, RandomAccessIterator1 last1, RandomAccessIterator2 first2, typename std::iterator_traits< RandomAccessIterator1 >::value_type init=typename std::iterator_traits< RandomAccessIterator1 >::value_type()) |
| Computes the inner_product of two ranges X and Y:
. More... | |
| template<typename Vector1 , typename Vector2 > | |
| Vector1::value_type | slip::inner_product (const Vector1 &V1, const Vector2 &V2) |
| Computes the inner_product of two ranges X and Y:
. More... | |
| template<typename RandomAccessIterator1 , typename RandomAccessIterator2d , typename RandomAccessIterator2 > | |
| std::iterator_traits < RandomAccessIterator2 > ::value_type | slip::gen_inner_product (RandomAccessIterator1 first1, RandomAccessIterator1 last1, RandomAccessIterator2d A_upper_left, RandomAccessIterator2d A_bottom_right, RandomAccessIterator2 first2, RandomAccessIterator2 last2, typename std::iterator_traits< RandomAccessIterator2 >::value_type init=typename std::iterator_traits< RandomAccessIterator2 >::value_type()) |
| Computes the generalized inner_product of two ranges:
. More... | |
| template<typename Vector1 , typename Matrix , typename Vector2 > | |
| Vector2::value_type | slip::gen_inner_product (const Vector1 &X, const Matrix &M, const Vector2 &Y) |
| Computes the generalized inner_product of two ranges:
. More... | |
| template<typename RandomAccessIterator1 , typename RandomAccessIterator2d > | |
| std::iterator_traits < RandomAccessIterator1 > ::value_type | slip::rayleigh (RandomAccessIterator1 first1, RandomAccessIterator1 last1, RandomAccessIterator2d A_upper_left, RandomAccessIterator2d A_bottom_right) |
| Computes the rayleigh coefficient of a vector x:
. More... | |
| template<typename Vector , typename Matrix > | |
| Vector::value_type | slip::rayleigh (const Vector &X, const Matrix &A) |
| Computes the rayleigh coefficient o f a vector x:
. More... | |
Marix norms | |
| template<typename InputIterator > | |
| slip::lin_alg_traits< typename std::iterator_traits < InputIterator >::value_type > ::value_type | slip::L22_norm_cplx (InputIterator first, InputIterator last) |
Computes the L22 norm 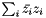 of a complex container. More... of a complex container. More... | |
| template<typename RandomAccessIterator2d > | |
| slip::lin_alg_traits< typename std::iterator_traits < RandomAccessIterator2d > ::value_type >::value_type | slip::row_norm (RandomAccessIterator2d upper_left, RandomAccessIterator2d bottom_right) |
Computes the row norm ( 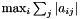 ) of a 2d range. More... ) of a 2d range. More... | |
| template<typename Container2d > | |
| slip::lin_alg_traits< typename Container2d::value_type > ::value_type | slip::row_norm (const Container2d &container) |
Computes the row norm ( 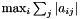 ) of a Container2d. More... ) of a Container2d. More... | |
| template<typename RandomAccessIterator2d > | |
| slip::lin_alg_traits< typename std::iterator_traits < RandomAccessIterator2d > ::value_type >::value_type | slip::col_norm (RandomAccessIterator2d upper_left, RandomAccessIterator2d bottom_right) |
Computes the column norm ( 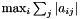 ) of a 2d range. More... ) of a 2d range. More... | |
| template<typename Container2d > | |
| slip::lin_alg_traits< typename Container2d::value_type > ::value_type | slip::col_norm (const Container2d &container) |
Computes the column norm ( 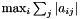 ) of a Container2d. More... ) of a Container2d. More... | |
| template<typename RandomAccessIterator2d > | |
| slip::lin_alg_traits< typename std::iterator_traits < RandomAccessIterator2d > ::value_type >::value_type | slip::frobenius_norm (RandomAccessIterator2d upper_left, RandomAccessIterator2d bottom_right) |
Computes the Frobenius norm ( 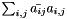 ) of a 2d range. More... ) of a 2d range. More... | |
| template<typename Container2d > | |
| slip::lin_alg_traits< typename Container2d::value_type > ::value_type | slip::frobenius_norm (const Container2d &container) |
Computes the Frobenius norm ( 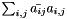 ) of a Container2d. More... ) of a Container2d. More... | |
Diagonal algorithms | |
| template<typename Container2d , typename RandomAccessIterator1 > | |
| void | slip::get_diagonal (const Container2d &container, RandomAccessIterator1 diag_first, RandomAccessIterator1 diag_last, const int diag_number=0) |
| Get the diagonal diag_number of a 2d container. More... | |
| template<typename Container2d , typename RandomAccessIterator1 > | |
| void | slip::set_diagonal (RandomAccessIterator1 diag_first, RandomAccessIterator1 diag_last, Container2d &container, const int diag_number=0) |
| Set the diagonal [diag_first,diag_last) in the diagonal diag_number of a 2d container. More... | |
| template<typename Container2d > | |
| void | slip::fill_diagonal (Container2d &container, const typename Container2d::value_type &val, const int diag_number=0) |
| Fill the diagonal diag_number of a 2d container with the value val. More... | |
| template<typename MatrixIterator > | |
| void | slip::fill_diagonal (MatrixIterator M_up, MatrixIterator M_bot, const typename MatrixIterator::value_type &val, const int diag_number=0) |
| Fill the diagonal diag_number of a 2d range with the value val. More... | |
Matrix generators | |
| template<typename Matrix > | |
| Matrix | slip::identity (const std::size_t nr, const std::size_t nc) |
| Returns an identity matrix which dimensions are nr*nc. More... | |
| template<typename MatrixIterator > | |
| void | slip::identity (MatrixIterator A_up, MatrixIterator A_bot) |
| Set a 2d range to the identity matrix. More... | |
| template<typename Matrix > | |
| void | slip::identity (Matrix &A) |
| Replaces A with the identity matrix. More... | |
| template<typename Matrix > | |
| void | slip::hilbert (Matrix &A) |
| Replaces A with the Hilbert matrix:
. More... | |
| template<typename RandomAccessIterator , typename Matrix > | |
| void | slip::toeplitz (RandomAccessIterator first, RandomAccessIterator last, Matrix &A) |
| Constructs the Toeplitz matrix from given a range. More... | |
Matrix tests | |
| template<typename Matrix > | |
| bool | slip::is_squared (const Matrix &A) |
| Test if a matrix is squared. More... | |
| template<typename MatrixIterator1 > | |
| bool | slip::is_squared (MatrixIterator1 A_up, MatrixIterator1 A_bot) |
| Test if a matrix is squared. More... | |
| template<typename Matrix > | |
| bool | slip::is_identity (const Matrix &A, const typename slip::lin_alg_traits< typename Matrix::value_type >::value_type tol=slip::epsilon< typename Matrix::value_type >()) |
| Test if a matrix is identity. More... | |
| template<typename MatrixIterator1 > | |
| bool | slip::is_diagonal (MatrixIterator1 A_up, MatrixIterator1 A_bot, const typename slip::lin_alg_traits< typename std::iterator_traits< MatrixIterator1 >::value_type >::value_type tol=slip::epsilon< typename std::iterator_traits< MatrixIterator1 >::value_type >()) |
| Test if a matrix is diagonal. More... | |
| template<typename Matrix > | |
| bool | slip::is_diagonal (const Matrix &A, const typename slip::lin_alg_traits< typename Matrix::value_type >::value_type tol=slip::epsilon< typename Matrix::value_type >()) |
| Test if a matrix is diagonal. More... | |
| template<typename MatrixIterator1 > | |
| bool | slip::is_hermitian (MatrixIterator1 A_up, MatrixIterator1 A_bot, const typename slip::lin_alg_traits< typename std::iterator_traits< MatrixIterator1 >::value_type >::value_type tol=slip::epsilon< typename std::iterator_traits< MatrixIterator1 >::value_type >()) |
| Test if a matrix is hermitian. More... | |
| template<typename Matrix > | |
| bool | slip::is_hermitian (const Matrix &A, const typename slip::lin_alg_traits< typename Matrix::value_type >::value_type tol=slip::epsilon< typename Matrix::value_type >()) |
| Test if a matrix is hermitian. More... | |
| template<typename MatrixIterator1 > | |
| bool | slip::is_skew_hermitian (MatrixIterator1 A_up, MatrixIterator1 A_bot, const typename slip::lin_alg_traits< typename std::iterator_traits< MatrixIterator1 >::value_type >::value_type tol=slip::epsilon< typename std::iterator_traits< MatrixIterator1 >::value_type >()) |
| Test if a matrix is skew hermitian. More... | |
| template<typename Matrix > | |
| bool | slip::is_skew_hermitian (const Matrix &A, const typename slip::lin_alg_traits< typename Matrix::value_type >::value_type tol=slip::epsilon< typename Matrix::value_type >()) |
| Test if a matrix is skew hermitian. More... | |
| template<typename MatrixIterator1 > | |
| bool | slip::is_symmetric (MatrixIterator1 A_up, MatrixIterator1 A_bot, const typename slip::lin_alg_traits< typename std::iterator_traits< MatrixIterator1 >::value_type >::value_type tol=slip::epsilon< typename std::iterator_traits< MatrixIterator1 >::value_type >()) |
| Test if a matrix is symmetric. More... | |
| template<typename Matrix > | |
| bool | slip::is_symmetric (const Matrix &A, const typename slip::lin_alg_traits< typename Matrix::value_type >::value_type tol=slip::epsilon< typename Matrix::value_type >()) |
| Test if a matrix is symmetric. More... | |
| template<typename MatrixIterator1 > | |
| bool | slip::is_band_matrix (MatrixIterator1 A_up, MatrixIterator1 A_bot, const typename MatrixIterator1::size_type lower_band_width, const typename MatrixIterator1::size_type upper_band_width, const typename slip::lin_alg_traits< typename std::iterator_traits< MatrixIterator1 >::value_type >::value_type tol=slip::epsilon< typename std::iterator_traits< MatrixIterator1 >::value_type >()) |
| Test if a matrix is a band matrix. More... | |
| template<typename Matrix > | |
| bool | slip::is_band_matrix (const Matrix &A, const typename Matrix::size_type lower_band_width, const typename Matrix::size_type upper_band_width, const typename slip::lin_alg_traits< typename Matrix::value_type >::value_type tol=slip::epsilon< typename Matrix::value_type >()) |
| Test if a matrix is symmetric. More... | |
| template<typename MatrixIterator1 > | |
| bool | slip::is_tridiagonal (MatrixIterator1 A_up, MatrixIterator1 A_bot, const typename slip::lin_alg_traits< typename std::iterator_traits< MatrixIterator1 >::value_type >::value_type tol=slip::epsilon< typename std::iterator_traits< MatrixIterator1 >::value_type >()) |
| Test if a matrix is tridiagonal. More... | |
| template<typename Matrix > | |
| bool | slip::is_tridiagonal (const Matrix &A, const typename slip::lin_alg_traits< typename Matrix::value_type >::value_type tol=slip::epsilon< typename Matrix::value_type >()) |
| Test if a matrix is tridiagonal. More... | |
| template<typename MatrixIterator1 > | |
| bool | slip::is_upper_bidiagonal (MatrixIterator1 A_up, MatrixIterator1 A_bot, const typename slip::lin_alg_traits< typename std::iterator_traits< MatrixIterator1 >::value_type >::value_type tol=slip::epsilon< typename std::iterator_traits< MatrixIterator1 >::value_type >()) |
| Test if a matrix is upper_bidiagonal. More... | |
| template<typename Matrix > | |
| bool | slip::is_upper_bidiagonal (const Matrix &A, const typename slip::lin_alg_traits< typename Matrix::value_type >::value_type tol=slip::epsilon< typename Matrix::value_type >()) |
| Test if a matrix is upper bidiagonal. More... | |
| template<typename MatrixIterator1 > | |
| bool | slip::is_lower_bidiagonal (MatrixIterator1 A_up, MatrixIterator1 A_bot, const typename slip::lin_alg_traits< typename std::iterator_traits< MatrixIterator1 >::value_type >::value_type tol=slip::epsilon< typename std::iterator_traits< MatrixIterator1 >::value_type >()) |
| Test if a matrix is lower_bidiagonal. More... | |
| template<typename Matrix > | |
| bool | slip::is_lower_bidiagonal (const Matrix &A, const typename slip::lin_alg_traits< typename Matrix::value_type >::value_type tol=slip::epsilon< typename Matrix::value_type >()) |
| Test if a matrix is lower bidiagonal. More... | |
| template<typename MatrixIterator1 > | |
| bool | slip::is_upper_hessenberg (MatrixIterator1 A_up, MatrixIterator1 A_bot, const typename slip::lin_alg_traits< typename std::iterator_traits< MatrixIterator1 >::value_type >::value_type tol=slip::epsilon< typename std::iterator_traits< MatrixIterator1 >::value_type >()) |
| Test if a matrix is upper_hessenberg. More... | |
| template<typename Matrix > | |
| bool | slip::is_upper_hessenberg (const Matrix &A, const typename slip::lin_alg_traits< typename Matrix::value_type >::value_type tol=slip::epsilon< typename Matrix::value_type >()) |
| Test if a matrix is upper hessenber. More... | |
| template<typename MatrixIterator1 > | |
| bool | slip::is_lower_hessenberg (MatrixIterator1 A_up, MatrixIterator1 A_bot, const typename slip::lin_alg_traits< typename std::iterator_traits< MatrixIterator1 >::value_type >::value_type tol=slip::epsilon< typename std::iterator_traits< MatrixIterator1 >::value_type >()) |
| Test if a matrix is lower_hessenberg. More... | |
| template<typename Matrix > | |
| bool | slip::is_lower_hessenberg (const Matrix &A, const typename slip::lin_alg_traits< typename Matrix::value_type >::value_type tol=slip::epsilon< typename Matrix::value_type >()) |
| Test if a matrix is lower hessenber. More... | |
| template<typename MatrixIterator1 > | |
| bool | slip::is_upper_triangular (MatrixIterator1 A_up, MatrixIterator1 A_bot, const typename slip::lin_alg_traits< typename std::iterator_traits< MatrixIterator1 >::value_type >::value_type tol=slip::epsilon< typename std::iterator_traits< MatrixIterator1 >::value_type >()) |
| Test if a matrix is upper_triangular. More... | |
| template<typename Matrix > | |
| bool | slip::is_upper_triangular (const Matrix &A, const typename slip::lin_alg_traits< typename Matrix::value_type >::value_type tol=slip::epsilon< typename Matrix::value_type >()) |
| Test if a matrix is upper triangular. More... | |
| template<typename MatrixIterator1 > | |
| bool | slip::is_lower_triangular (MatrixIterator1 A_up, MatrixIterator1 A_bot, const typename slip::lin_alg_traits< typename std::iterator_traits< MatrixIterator1 >::value_type >::value_type tol=slip::epsilon< typename std::iterator_traits< MatrixIterator1 >::value_type >()) |
| Test if a matrix is lower_triangular. More... | |
| template<typename Matrix > | |
| bool | slip::is_lower_triangular (const Matrix &A, const typename slip::lin_alg_traits< typename Matrix::value_type >::value_type tol=slip::epsilon< typename Matrix::value_type >()) |
| Test if a matrix is lower triangular. More... | |
| template<typename MatrixIterator1 > | |
| bool | slip::is_null_diagonal (MatrixIterator1 A_up, MatrixIterator1 A_bot, int diag_number, const typename slip::lin_alg_traits< typename std::iterator_traits< MatrixIterator1 >::value_type >::value_type tol=slip::epsilon< typename std::iterator_traits< MatrixIterator1 >::value_type >()) |
| Test if a matrix has a nul diagonal. More... | |
| template<typename MatrixIterator1 > | |
| slip::DENSE_MATRIX_TYPE | slip::analyse_matrix (MatrixIterator1 A_up, MatrixIterator1 A_bot, const typename slip::lin_alg_traits< typename std::iterator_traits< MatrixIterator1 >::value_type >::value_type tol=slip::epsilon< typename std::iterator_traits< MatrixIterator1 >::value_type >()) |
| Analyse the type of a matrix. More... | |
Pivot algorithms | |
| template<typename MatrixIterator > | |
| int | slip::pivot_max (MatrixIterator M_up, MatrixIterator M_bot) |
| Returns the row position of the maximum partial pivot of a 2d range. More... | |
| template<typename MatrixIterator > | |
| int | slip::partial_pivot (MatrixIterator M_up, MatrixIterator M_bot) |
| Returns the partial pivot of a 2d range. More... | |
General inverse algorithm | |
| template<class Matrix1 , class Matrix2 > | |
| void | slip::inverse (const Matrix1 &M, const std::size_t nr1, const std::size_t nc1, Matrix2 &IM, const std::size_t nr2, const std::size_t nc2) |
| Computes the inverse of a matrix using gaussian elimination. More... | |
| template<class Matrix1 , class Matrix2 > | |
| void | slip::inverse (const Matrix1 &M, Matrix2 &IM) |
| Computes the inverse of a matrix using gaussian elimination. More... | |
LU algorithms | |
| template<class Matrix1 , class Matrix2 , class Vector > | |
| int | slip::lu (const Matrix1 &M, Matrix2 &LU, Vector &Indx) |
| Computes the LU decomposition according to rows permutations of a matrix using Crout method
LU is composed of L and U as following:
Indx is a vector that records the row permutations effected by the partial pivoting. More... | |
| template<class Matrix1 , class Matrix2 > | |
| int | slip::lu (const Matrix1 &M, Matrix2 &L, Matrix2 &U, Matrix2 &P) |
| template<class Matrix , class Vector1 , class Vector2 , class Vector3 > | |
| void | slip::lu_solve (const Matrix LU, const std::size_t nr, const std::size_t nc, const Vector1 &Indx, const std::size_t nv1, const Vector2 &B, const std::size_t nv2, Vector3 &X, const std::size_t nv3) |
| Solve Linear Equation using LU decomposition. More... | |
| template<class Matrix , class Vector1 , class Vector2 > | |
| void | slip::lu_solve (const Matrix &A, Vector1 &X, const Vector2 &B) |
| Solve Linear Equation AX = B using LU decomposition. More... | |
| template<class Matrix1 , class Matrix2 > | |
| void | slip::lu_inv (const Matrix1 &M, Matrix2 &IM) |
| Computes the inverse of a matrix using LU decomposition. More... | |
| template<class Matrix1 > | |
| Matrix1::value_type | slip::lu_det (const Matrix1 &M) |
| Computes the determinant of a matrix using LU decomposition. More... | |
Triangular matrix algorithms | |
| template<typename MatrixIterator , typename RandomAccessIterator1 , typename RandomAccessIterator2 > | |
| void | slip::upper_triangular_solve (MatrixIterator U_up, MatrixIterator U_bot, RandomAccessIterator1 X_first, RandomAccessIterator1 X_last, RandomAccessIterator2 B_first, RandomAccessIterator2 B_last, typename slip::lin_alg_traits< typename MatrixIterator::value_type >::value_type precision) |
| Solve the linear system U*X=B when U is upper triangular
. More... | |
| template<class Matrix , class Vector1 , class Vector2 > | |
| void | slip::upper_triangular_solve (const Matrix &U, Vector1 &X, const Vector2 &B, typename slip::lin_alg_traits< typename Matrix::value_type >::value_type precision) |
| Solve the linear system U*X=B when U is upper triangular
. More... | |
| template<typename MatrixIterator1 , typename MatrixIterator2 > | |
| void | slip::upper_triangular_inv (MatrixIterator1 A_up, MatrixIterator1 A_bot, MatrixIterator2 Ainv_up, MatrixIterator2 Ainv_bot, typename slip::lin_alg_traits< typename MatrixIterator1::value_type >::value_type precision=typename slip::lin_alg_traits< typename MatrixIterator1::value_type >::value_type(1.0E-6)) |
| Invert an upper triangular Matrix
. More... | |
| template<typename Matrix1 , typename Matrix2 > | |
| void | slip::upper_triangular_inv (Matrix1 A, Matrix2 Ainv, typename slip::lin_alg_traits< typename Matrix1::value_type >::value_type precision=typename slip::lin_alg_traits< typename Matrix1::value_type >::value_type(1.0E-6)) |
| Invert an upper triangular Matrix
. More... | |
| template<typename MatrixIterator , typename RandomAccessIterator1 , typename RandomAccessIterator2 > | |
| void | slip::lower_triangular_solve (MatrixIterator L_up, MatrixIterator L_bot, RandomAccessIterator1 X_first, RandomAccessIterator1 X_last, RandomAccessIterator2 B_first, RandomAccessIterator2 B_last, typename slip::lin_alg_traits< typename MatrixIterator::value_type >::value_type precision) |
| Solve the linear system L*X=B when L is lower triangular
. More... | |
| template<class Matrix , class Vector1 , class Vector2 > | |
| void | slip::lower_triangular_solve (const Matrix &L, Vector1 &X, const Vector2 &B, typename slip::lin_alg_traits< typename Matrix::value_type >::value_type precision) |
| Solve the linear system L*X=B when L is lower triangular
. More... | |
| template<typename MatrixIterator1 , typename MatrixIterator2 > | |
| void | slip::lower_triangular_inv (MatrixIterator1 A_up, MatrixIterator1 A_bot, MatrixIterator2 Ainv_up, MatrixIterator2 Ainv_bot, typename slip::lin_alg_traits< typename MatrixIterator1::value_type >::value_type precision=typename slip::lin_alg_traits< typename MatrixIterator1::value_type >::value_type(1.0E-6)) |
| Invert a lower triangular Matrix
. More... | |
| template<typename Matrix1 , typename Matrix2 > | |
| void | slip::lower_triangular_inv (const Matrix1 &A, Matrix2 &Ainv, typename slip::lin_alg_traits< typename Matrix1::value_type >::value_type precision=typename slip::lin_alg_traits< typename Matrix1::value_type >::value_type(1.0E-6)) |
| Invert a lower triangular Matrix
. More... | |
| template<typename MatrixIterator , typename RandomAccessIterator1 , typename RandomAccessIterator2 > | |
| void | slip::unit_upper_triangular_solve (MatrixIterator U_up, MatrixIterator U_bot, RandomAccessIterator1 X_first, RandomAccessIterator1 X_last, RandomAccessIterator2 B_first, RandomAccessIterator2 B_last) |
| Solve the linear system U*X=B when U is unit upper triangular
. More... | |
| template<class Matrix , class Vector1 , class Vector2 > | |
| void | slip::unit_upper_triangular_solve (const Matrix &U, Vector1 &X, const Vector2 &B) |
| Solve the linear system U*X=B when U is unit upper triangular
. More... | |
| template<typename MatrixIterator , typename RandomAccessIterator1 , typename RandomAccessIterator2 > | |
| void | slip::unit_lower_triangular_solve (MatrixIterator L_up, MatrixIterator L_bot, RandomAccessIterator1 X_first, RandomAccessIterator1 X_last, RandomAccessIterator2 B_first, RandomAccessIterator2 B_last) |
| Solve the linear system L*X=B when L is unit lower triangular
. More... | |
| template<class Matrix , class Vector1 , class Vector2 > | |
| void | slip::unit_lower_triangular_solve (const Matrix &L, Vector1 &X, const Vector2 &B) |
| Solve the linear system L*X=B when L is unit lower triangular
. More... | |
Diagonal matrix algorithms | |
| template<typename RandomAccessIterator1 , typename RandomAccessIterator2 , typename RandomAccessIterator3 > | |
| void | slip::diagonal_solve (RandomAccessIterator1 first, RandomAccessIterator1 last, RandomAccessIterator2 X_first, RandomAccessIterator2 X_last, RandomAccessIterator3 B_first, RandomAccessIterator3 B_last, typename slip::lin_alg_traits< typename std::iterator_traits< RandomAccessIterator1 >::value_type >::value_type precision) |
| Solve the linear system D*X=B when D a diagonal matrix
. More... | |
Band matrix algorithms | |
| template<typename MatrixIterator1 , typename RandomAccessIterator > | |
| int | slip::band_lu (MatrixIterator1 A_up, MatrixIterator1 A_bot, const int p, const int q, RandomAccessIterator Ind_first, RandomAccessIterator Ind_last, typename slip::lin_alg_traits< typename MatrixIterator1::value_type >::value_type precision) |
in place Band LU decomposition a square band Matrix A 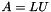 with L a p lower band matrix and U a q upper band matrix More... with L a p lower band matrix and U a q upper band matrix More... | |
| template<class Matrix1 , class Matrix2 , class Matrix3 , class Matrix4 > | |
| int | slip::band_lu (const Matrix1 &M, const int p, const int q, Matrix2 &L, Matrix3 &U, Matrix4 &P, typename slip::lin_alg_traits< typename Matrix1::value_type >::value_type precision) |
in place Band LU decomposition a square band Matrix A 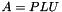 with L a p lower band matrix and U a q upper band matrix and P the permutation matrix. More... with L a p lower band matrix and U a q upper band matrix and P the permutation matrix. More... | |
| template<typename MatrixIterator , typename RandomAccessIterator1 , typename RandomAccessIterator2 > | |
| void | slip::upper_band_solve (MatrixIterator U_up, MatrixIterator U_bot, int q, RandomAccessIterator1 X_first, RandomAccessIterator1 X_last, RandomAccessIterator2 B_first, RandomAccessIterator2 B_last, typename slip::lin_alg_traits< typename MatrixIterator::value_type >::value_type precision) |
| Solve the linear system U*X=B when U is q width upper banded
. More... | |
| template<typename MatrixIterator , typename RandomAccessIterator1 , typename RandomAccessIterator2 > | |
| void | slip::unit_upper_band_solve (MatrixIterator U_up, MatrixIterator U_bot, int q, RandomAccessIterator1 X_first, RandomAccessIterator1 X_last, RandomAccessIterator2 B_first, RandomAccessIterator2 B_last, typename slip::lin_alg_traits< typename MatrixIterator::value_type >::value_type precision) |
| Solve the linear system U*X=B when U is unit q width upper banded
. More... | |
| template<typename MatrixIterator , typename RandomAccessIterator1 , typename RandomAccessIterator2 > | |
| void | slip::lower_band_solve (MatrixIterator L_up, MatrixIterator L_bot, int p, RandomAccessIterator1 X_first, RandomAccessIterator1 X_last, RandomAccessIterator2 B_first, RandomAccessIterator2 B_last, typename slip::lin_alg_traits< typename MatrixIterator::value_type >::value_type precision) |
| Solve the linear system L*X=B when L is p lower banded
. More... | |
| template<typename MatrixIterator , typename RandomAccessIterator1 , typename RandomAccessIterator2 > | |
| void | slip::unit_lower_band_solve (MatrixIterator L_up, MatrixIterator L_bot, int p, RandomAccessIterator1 X_first, RandomAccessIterator1 X_last, RandomAccessIterator2 B_first, RandomAccessIterator2 B_last) |
| Solve the linear system L*X=B when L is unit p lower banded
. More... | |
Gauss system solve algorithms | |
| template<class Matrix , class Vector1 , class Vector2 > | |
| bool | slip::gauss_solve (const Matrix &M, Vector1 &X, const Vector2 &B, typename slip::lin_alg_traits< typename Matrix::value_type >::value_type precision) |
| Solve the linear system M*X=B using the Gauss elemination partial pivoting. More... | |
| template<class Matrix , class Vector1 , class Vector2 > | |
| bool | slip::gauss_solve_with_filling (const Matrix &M, Vector1 &X, const Vector2 &B, typename slip::lin_alg_traits< typename Matrix::value_type >::value_type precision) |
| Solve the linear system M*X=B with the Gauss pivot method, the null pivot are replaced by precision. More... | |
Tridiagonal matrix algorithms | |
| template<typename RandomAccessIterator1 , typename RandomAccessIterator2 , typename RandomAccessIterator3 > | |
| void | slip::tridiagonal_lu (RandomAccessIterator1 diag_first, RandomAccessIterator1 diag_last, RandomAccessIterator1 up_diag_first, RandomAccessIterator1 up_diag_last, RandomAccessIterator1 low_diag_first, RandomAccessIterator1 low_diag_last, RandomAccessIterator2 L_low_first, RandomAccessIterator2 L_low_last, RandomAccessIterator3 U_up_first, RandomAccessIterator3 U_up_last, typename slip::lin_alg_traits< typename std::iterator_traits< RandomAccessIterator1 >::value_type >::value_type precision=typename slip::lin_alg_traits< typename std::iterator_traits< RandomAccessIterator1 >::value_type >::value_type(1.0E-6)) |
| Computes the LU decomposition for a tridiagonal matrix
. More... | |
Bidiagonal matrix algorithms | |
| template<typename RandomAccessIterator1 , typename RandomAccessIterator2 , typename RandomAccessIterator3 > | |
| void | slip::unit_lower_bidiagonal_solve (RandomAccessIterator1 low_diag_first, RandomAccessIterator1 low_diag_last, RandomAccessIterator2 X_first, RandomAccessIterator2 X_last, RandomAccessIterator3 B_first, RandomAccessIterator3 B_last) |
| solve Ax = B with A unit lower bidiagonal
| |
| template<typename RandomAccessIterator1 , typename RandomAccessIterator2d > | |
| void | slip::unit_lower_bidiagonal_inv (RandomAccessIterator1 low_diag_first, RandomAccessIterator1 low_diag_last, RandomAccessIterator2d Ainv_up, RandomAccessIterator2d Ainv_bot) |
| Invert a lower unit bidiagonal matrix:
. More... | |
| template<typename RandomAccessIterator1 , typename RandomAccessIterator2 , typename RandomAccessIterator3 > | |
| void | slip::lower_bidiagonal_solve (RandomAccessIterator1 diag_first, RandomAccessIterator1 diag_last, RandomAccessIterator1 low_diag_first, RandomAccessIterator1 low_diag_last, RandomAccessIterator2 X_first, RandomAccessIterator2 X_last, RandomAccessIterator3 B_first, RandomAccessIterator3 B_last, typename slip::lin_alg_traits< typename std::iterator_traits< RandomAccessIterator1 >::value_type >::value_type precision=typename slip::lin_alg_traits< typename std::iterator_traits< RandomAccessIterator1 >::value_type >::value_type(1.0E-6)) |
| solve Ax = B with A lower bidiagonal
| |
| template<typename RandomAccessIterator1 , typename RandomAccessIterator2d > | |
| void | slip::lower_bidiagonal_inv (RandomAccessIterator1 diag_first, RandomAccessIterator1 diag_last, RandomAccessIterator1 low_diag_first, RandomAccessIterator1 low_diag_last, RandomAccessIterator2d Ainv_up, RandomAccessIterator2d Ainv_bot, typename slip::lin_alg_traits< typename std::iterator_traits< RandomAccessIterator1 >::value_type >::value_type precision=typename slip::lin_alg_traits< typename std::iterator_traits< RandomAccessIterator1 >::value_type >::value_type(1.0E-6)) |
| Invert a lower bidiagonal matrix:
. More... | |
| template<typename Container2d1 , typename Container2d2 > | |
| void | slip::lower_bidiagonal_inv (const Container2d1 &A, Container2d2 &Ainv, typename slip::lin_alg_traits< typename Container2d1::value_type >::value_type precision=typename slip::lin_alg_traits< typename Container2d1::value_type >::value_type(1.0E-6)) |
| Invert a lower bidiagonal matrix:
. More... | |
| template<typename RandomAccessIterator1 , typename RandomAccessIterator2 , typename RandomAccessIterator3 > | |
| void | slip::upper_bidiagonal_solve (RandomAccessIterator1 diag_first, RandomAccessIterator1 diag_last, RandomAccessIterator1 up_diag_first, RandomAccessIterator1 up_diag_last, RandomAccessIterator2 X_first, RandomAccessIterator2 X_last, RandomAccessIterator3 B_first, RandomAccessIterator3 B_last, typename slip::lin_alg_traits< typename std::iterator_traits< RandomAccessIterator1 >::value_type >::value_type precision=typename slip::lin_alg_traits< typename std::iterator_traits< RandomAccessIterator1 >::value_type >::value_type(1.0E-6)) |
| solve Ax = B with A upper bidiagonal
| |
| template<typename RandomAccessIterator1 , typename RandomAccessIterator2d > | |
| void | slip::upper_bidiagonal_inv (RandomAccessIterator1 diag_first, RandomAccessIterator1 diag_last, RandomAccessIterator1 up_diag_first, RandomAccessIterator1 up_diag_last, RandomAccessIterator2d Ainv_up, RandomAccessIterator2d Ainv_bot, typename slip::lin_alg_traits< typename std::iterator_traits< RandomAccessIterator1 >::value_type >::value_type precision=typename slip::lin_alg_traits< typename std::iterator_traits< RandomAccessIterator1 >::value_type >::value_type(1.0E-6)) |
| Invert an upper bidiagonal squared matrix
. More... | |
| template<typename Container2d1 , typename Container2d2 > | |
| void | slip::upper_bidiagonal_inv (const Container2d1 &A, Container2d2 &Ainv, typename slip::lin_alg_traits< typename Container2d1::value_type >::value_type precision=typename slip::lin_alg_traits< typename Container2d1::value_type >::value_type(1.0E-6)) |
| Invert an upper bidiagonal squared matrix
. More... | |
| template<typename RandomAccessIterator1 , typename RandomAccessIterator2 , typename RandomAccessIterator3 > | |
| void | slip::unit_upper_bidiagonal_solve (RandomAccessIterator1 up_diag_first, RandomAccessIterator1 up_diag_last, RandomAccessIterator2 X_first, RandomAccessIterator2 X_last, RandomAccessIterator3 B_first, RandomAccessIterator3 B_last) |
| solve Ax = B with A unit upper bidiagonal
| |
| template<typename RandomAccessIterator1 , typename RandomAccessIterator2d > | |
| void | slip::unit_upper_bidiagonal_inv (RandomAccessIterator1 up_diag_first, RandomAccessIterator1 up_diag_last, RandomAccessIterator2d Ainv_up, RandomAccessIterator2d Ainv_bot) |
| Invert an unit upper bidiagonal matrix:
. More... | |
Tridiagonal system solve algorithms | |
| template<typename RandomAccessIterator1 , typename RandomAccessIterator2 , typename RandomAccessIterator3 > | |
| void | slip::thomas_solve (RandomAccessIterator1 diag_first, RandomAccessIterator1 diag_last, RandomAccessIterator1 up_diag_first, RandomAccessIterator1 up_diag_last, RandomAccessIterator1 low_diag_first, RandomAccessIterator1 low_diag_last, RandomAccessIterator2 X_first, RandomAccessIterator2 X_last, RandomAccessIterator3 B_first, RandomAccessIterator3 B_last, typename slip::lin_alg_traits< typename std::iterator_traits< RandomAccessIterator1 >::value_type >::value_type precision=typename slip::lin_alg_traits< typename std::iterator_traits< RandomAccessIterator1 >::value_type >::value_type(1.0E-6)) |
| Solve the tridiagonal system A*X=B with the Thomas method
. More... | |
| template<typename Container2d , typename Vector1 , typename Vector2 > | |
| void | slip::thomas_solve (const Container2d &A, Vector1 &X, const Vector2 &B, typename slip::lin_alg_traits< typename Container2d::value_type >::value_type precision=typename slip::lin_alg_traits< typename Container2d::value_type >::value_type(1.0E-6)) |
| Solve the tridiagonal system Tx=B
. More... | |
| template<typename RandomAccessIterator1 , typename RandomAccessIterator2d > | |
| void | slip::thomas_inv (RandomAccessIterator1 diag_first, RandomAccessIterator1 diag_last, RandomAccessIterator1 up_diag_first, RandomAccessIterator1 up_diag_last, RandomAccessIterator1 low_diag_first, RandomAccessIterator1 low_diag_last, RandomAccessIterator2d Ainv_up, RandomAccessIterator2d Ainv_bot, typename slip::lin_alg_traits< typename std::iterator_traits< RandomAccessIterator1 >::value_type >::value_type precision=typename slip::lin_alg_traits< typename std::iterator_traits< RandomAccessIterator1 >::value_type >::value_type(1.0E-6)) |
| Invert a tridiagonal squared matrix A with the Thomas method
. More... | |
| template<typename Container2d1 , typename Container2d2 > | |
| void | slip::thomas_inv (const Container2d1 &A, Container2d2 &Ainv, typename slip::lin_alg_traits< typename Container2d1::value_type >::value_type precision=typename slip::lin_alg_traits< typename Container2d1::value_type >::value_type(1.0E-6)) |
| Invert a tridiagonal squared matrix A with the Thomas method
. More... | |
Tridiagonal symmetric positive matrix algorithms | |
| template<typename RandomAccessIterator1 , typename RandomAccessIterator2 , typename RandomAccessIterator3 > | |
| void | slip::tridiagonal_cholesky (RandomAccessIterator1 diag_first, RandomAccessIterator1 diag_last, RandomAccessIterator1 up_diag_first, RandomAccessIterator1 up_diag_last, RandomAccessIterator2 R_diag_first, RandomAccessIterator2 R_diag_last, RandomAccessIterator3 R_low_first, RandomAccessIterator3 R_low_last) |
| Tridiagonal symmetric positive decomposition
where: | |
| template<typename RandomAccessIterator1 , typename RandomAccessIterator2 , typename RandomAccessIterator3 > | |
| void | slip::tridiagonal_cholesky_solve (RandomAccessIterator1 diag_first, RandomAccessIterator1 diag_last, RandomAccessIterator1 up_diag_first, RandomAccessIterator1 up_diag_last, RandomAccessIterator2 X_first, RandomAccessIterator2 X_last, RandomAccessIterator3 B_first, RandomAccessIterator3 B_last) |
| Solve the tridiagonal symmetric positive definite system T*X=B with the Cholesky method
where: | |
| template<typename Container2d , typename Vector1 , typename Vector2 > | |
| void | slip::tridiagonal_cholesky_solve (const Container2d &A, Vector1 &X, const Vector2 &B) |
| Solve the tridiagonal symmetric positive definite system T*X=B with the Cholesky method
where: | |
| template<typename RandomAccessIterator1 , typename RandomAccessIterator2d > | |
| void | slip::tridiagonal_cholesky_inv (RandomAccessIterator1 diag_first, RandomAccessIterator1 diag_last, RandomAccessIterator1 up_diag_first, RandomAccessIterator1 up_diag_last, RandomAccessIterator2d Ainv_up, RandomAccessIterator2d Ainv_bot) |
| Invert the tridiagonal symmetric positive definite system T:
where: | |
| template<typename Container2d1 , typename Container2d2 > | |
| void | slip::tridiagonal_cholesky_inv (const Container2d1 &A, Container2d2 &Ainv) |
| Invert the tridiagonal symmetric positive definite system T:
where: | |
LDLT algorithms | |
| template<typename Container2d > | |
| void | slip::LDLT_decomposition (Container2d &A) |
| in place LU decomposition for symmetric matrix
| |
| template<typename Matrix1 , typename Matrix2 , typename Vector1 , typename Matrix3 > | |
| void | slip::LDLT_decomposition (const Matrix1 &A, Matrix2 &L, Vector1 &D, Matrix3 <) |
| in place LU decomposition for symmetric matrix
| |
| template<typename Matrix1 , typename Vector1 , typename Vector2 > | |
| void | slip::LDLT_solve (const Matrix1 &A, Vector1 &X, const Vector2 &B) |
LDLT solve of system AX = B with A a square symmetric Matrix. 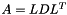 with L a lower triangular matrix. More... with L a lower triangular matrix. More... | |
Square hermitian or symmetric matrix algorithms | |
| template<typename MatrixIterator1 , typename MatrixIterator2 , typename MatrixIterator3 > | |
| void | slip::cholesky_cplx (MatrixIterator1 A_up, MatrixIterator1 A_bot, MatrixIterator2 L_up, MatrixIterator2 L_bot, MatrixIterator3 LH_up, MatrixIterator3 LH_bot) |
cholesky decomposition of a square hermitian positive definite Matrix. 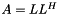 with L a lower triangular matrix More... with L a lower triangular matrix More... | |
| template<typename MatrixIterator1 > | |
| void | slip::cholesky_cplx (MatrixIterator1 A_up, MatrixIterator1 A_bot) |
cholesky decomposition of a square hermitian positive definite Matrix. 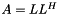 with L a lower triangular matrix. L is stored in the lower triangular part of A, with L a lower triangular matrix. L is stored in the lower triangular part of A, 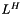 is stored in the upper triangular part of A. More... is stored in the upper triangular part of A. More... | |
| template<typename MatrixIterator1 , typename MatrixIterator2 , typename MatrixIterator3 > | |
| void | slip::cholesky_real (MatrixIterator1 A_up, MatrixIterator1 A_bot, MatrixIterator2 L_up, MatrixIterator2 L_bot, MatrixIterator3 LH_up, MatrixIterator3 LH_bot) |
cholesky decomposition of a square real symmetric and positive definite Matrix. 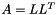 with L a lower triangular matrix. More... with L a lower triangular matrix. More... | |
| template<typename MatrixIterator1 > | |
| void | slip::cholesky_real (MatrixIterator1 A_up, MatrixIterator1 A_bot) |
cholesky decomposition of a square real symmetric and positive definite Matrix. 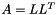 with L a lower triangular matrix. L is stored in the lower triangular part of A, with L a lower triangular matrix. L is stored in the lower triangular part of A, 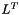 is stored in the upper triangular part of A. More... is stored in the upper triangular part of A. More... | |
| template<class Matrix1 , class Matrix2 , class Matrix3 > | |
| void | slip::cholesky_real (const Matrix1 &A, Matrix2 &L, Matrix3 <) |
cholesky decomposition of a square real symmetric positive definite Matrix. 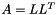 with L a lower triangular matrix More... with L a lower triangular matrix More... | |
| template<class Matrix1 , class Matrix2 , class Matrix3 > | |
| void | slip::cholesky_cplx (const Matrix1 &A, Matrix2 &L, Matrix3 <) |
cholesky decomposition of a square hermitian positive definite Matrix. 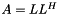 with L a lower triangular matrix More... with L a lower triangular matrix More... | |
| template<class Matrix1 , class Matrix2 , class Matrix3 > | |
| void | slip::cholesky (const Matrix1 &A, Matrix2 &L, Matrix3 <) |
cholesky decomposition of a square hermitian positive definite Matrix. 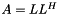 with L a lower triangular matrix More... with L a lower triangular matrix More... | |
| template<class Matrix1 > | |
| void | slip::cholesky (Matrix1 &A) |
cholesky decomposition of a square hermitian positive definite Matrix. 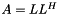 with L a lower triangular matrix. L is stored in the lower triangular part of A, with L a lower triangular matrix. L is stored in the lower triangular part of A, 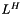 is stored in the upper triangular part of A. More... is stored in the upper triangular part of A. More... | |
| template<typename MatrixIterator , typename RandomAccessIterator1 , typename RandomAccessIterator2 > | |
| void | slip::cholesky_solve (MatrixIterator A_up, MatrixIterator A_bot, RandomAccessIterator1 X_first, RandomAccessIterator1 X_last, RandomAccessIterator2 B_first, RandomAccessIterator2 B_last, typename slip::lin_alg_traits< typename MatrixIterator::value_type >::value_type precision=typename slip::lin_alg_traits< typename MatrixIterator::value_type >::value_type(1.0E-6)) |
| cholesky solve of system AX = B with A a square hermitian positive definite Matrix. More... | |
| template<class Matrix1 , class Vector1 , class Vector2 > | |
| void | slip::cholesky_solve (const Matrix1 &A, Vector1 &X, const Vector2 &B, typename slip::lin_alg_traits< typename Matrix1::value_type >::value_type precision=typename slip::lin_alg_traits< typename Matrix1::value_type >::value_type(1.0E-6)) |
| cholesky solve of system AX = B with A a square hermitian positive definite Matrix. More... | |
| template<typename MatrixIterator1 , typename MatrixIterator2 > | |
| void | slip::cholesky_inv (MatrixIterator1 A_up, MatrixIterator1 A_bot, MatrixIterator2 Ainv_up, MatrixIterator2 Ainv_bot, typename slip::lin_alg_traits< typename MatrixIterator1::value_type >::value_type precision=typename slip::lin_alg_traits< typename MatrixIterator1::value_type >::value_type(1.0E-6)) |
| cholesky inverse of a square hermitian positive definite Matrix A. More... | |
| template<typename Matrix1 , typename Matrix2 > | |
| void | slip::cholesky_inv (Matrix1 A, Matrix2 Ainv, typename slip::lin_alg_traits< typename Matrix1::value_type >::value_type precision=typename slip::lin_alg_traits< typename Matrix1::value_type >::value_type(1.0E-6)) |
| cholesky inverse of a square hermitian positive definite Matrix A. More... | |
Givens rotations algorithms | |
| template<typename Real > | |
| void | slip::rotgen (Real &a, Real &b, Real &cos, Real &sin) |
| Computes the Givens sinus and cosinus. More... | |
| template<typename Real > | |
| void | slip::givens_sin_cos (const Real &xi, const Real &xk, Real &sin, Real &cos) |
| Computes the Givens sinus and cosinus.
. More... | |
| template<typename Complex > | |
| void | slip::complex_givens_sin_cos (const Complex &xi, const Complex &xk, Complex &sin, typename Complex::value_type &cos) |
| Computes the complex Givens sinus and cosinus.
with
. More... | |
| template<typename Matrix , typename SizeType , typename Real > | |
| void | slip::left_givens (Matrix &M, const SizeType &row1, const SizeType &row2, const Real &sinus, const Real &cosinus, const SizeType &col1, const SizeType &col2) |
| Apply left Givens rotation multiplication. More... | |
| template<typename Matrix , typename SizeType , typename Real > | |
| void | slip::right_givens (Matrix &M, const SizeType &col1, const SizeType &col2, const Real &sinus, const Real &cosinus, const SizeType &row1, const SizeType &row2) |
| Apply right Givens rotation multiplication. More... | |
| template<typename Matrix , typename SizeType , typename Complex > | |
| void | slip::complex_left_givens (Matrix &M, const SizeType &row1, const SizeType &row2, const Complex &sinus, const typename Complex::value_type &cosinus, const SizeType &col1, const SizeType &col2) |
| Apply complex left Givens rotation multiplication. More... | |
| template<typename Matrix , typename SizeType , typename Complex > | |
| void | slip::complex_right_givens (Matrix &M, const SizeType &col1, const SizeType &col2, const Complex &sinus, const typename Complex::value_type &cosinus, const SizeType &row1, const SizeType &row2) |
| Apply complex right Givens rotation multiplication. More... | |
Householder algorithms | |
| template<typename VectorIterator1 , typename VectorIterator2 > | |
| void | slip::housegen (VectorIterator1 a_begin, VectorIterator1 a_end, VectorIterator2 u_begin, VectorIterator2 u_end, typename std::iterator_traits< VectorIterator1 >::value_type &nu) |
| Compute the Householder vector u of a vector a. More... | |
| template<typename RandomAccessIterator , typename MatrixIterator1 > | |
| void | slip::right_householder_update (RandomAccessIterator V_first, RandomAccessIterator V_last, MatrixIterator1 M_up, MatrixIterator1 M_bot) |
| right multiplies the matrix M with the Householder matrix P:
| |
| template<typename RandomAccessIterator , typename MatrixIterator1 > | |
| void | slip::left_householder_update (RandomAccessIterator V_first, RandomAccessIterator V_last, MatrixIterator1 M_up, MatrixIterator1 M_bot) |
| Left multiplies the Householder matrix P with the matrix M:
. More... | |
| template<typename Matrix1 , typename Vector1 , typename Matrix2 > | |
| void | slip::left_householder_accumulate (const Matrix1 &M, const Vector1 &V0, Matrix2 &Q) |
| Computes Q = Q1Q2...Qn from the inplace Householder QR decomposition. More... | |
Hessenberg reduction | |
| template<typename Matrix1 > | |
| void | slip::householder_hessenberg (Matrix1 &M) |
Householder Hessenberg reduction of the square matrix M. The result is overwritten in M. The Hessenberg decomposition is 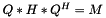 . More... . More... | |
| template<typename Matrix1 , typename Matrix2 > | |
| void | slip::householder_hessenberg (const Matrix1 &M, Matrix2 &H) |
Householder Hessenberg reduction of the square matrix M. The Hessenberg decomposition is 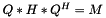 . More... . More... | |
| template<typename Matrix1 , typename Matrix2 , typename Matrix3 > | |
| void | slip::householder_hessenberg (const Matrix1 &M, Matrix2 &H, Matrix3 &Q) |
Householder Hessenberg reduction of the square matrix M. The Hessenberg decomposition is 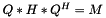 . More... . More... | |
 1.8.6
1.8.6