Provides some Singular Value Decomposition (SVD) algorithms. More...

#include <cmath>
#include <algorithm>
#include <limits>
#include "Vector.hpp"
#include "Array2d.hpp"
#include "linear_algebra.hpp"
#include "macros.hpp"
#include "norms.hpp"
#include "linear_algebra_traits.hpp"
#include "complex_cast.hpp"

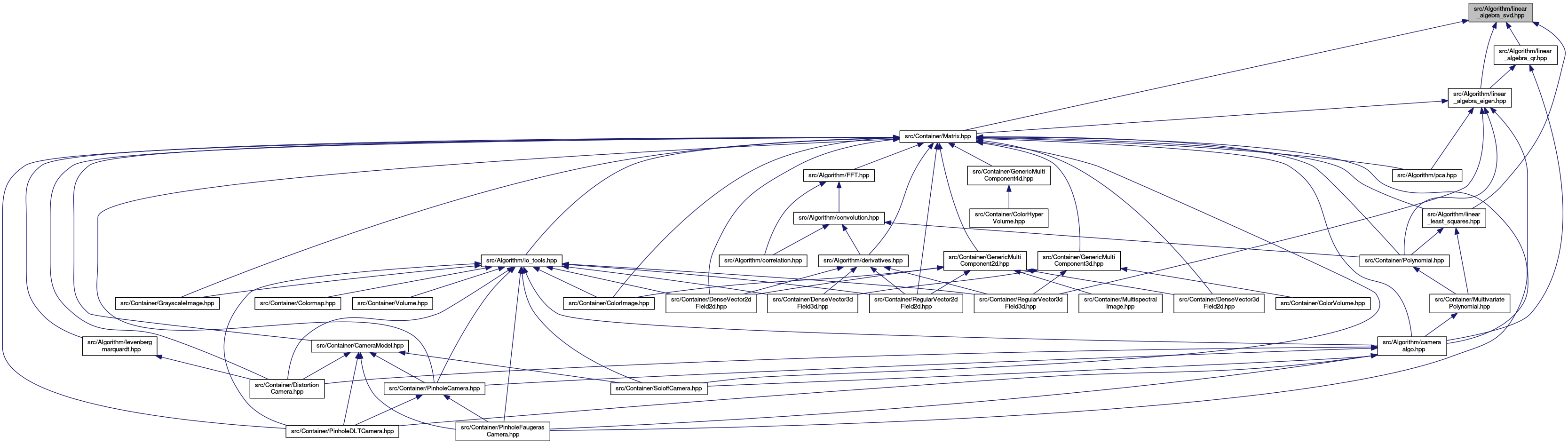
Include dependency graph for linear_algebra_svd.hpp:

This graph shows which files directly or indirectly include this file:

Go to the source code of this file.

Namespaces
	slip
	This namespace corresponds to the kernel of the Simple Library on Image Processing (SLIP). That is to say that it contains the data structures and the algorithms needed by these data strucutres.

Functions
SVD internal algorithms
template<typename Matrix1 , typename Vector , typename Matrix2 , typename Matrix3 >
void	slip::BiReduce (Matrix1 &X, Vector &d, Vector &e, Matrix2 &U, Matrix3 &V)
	BiReduce. Given an np matrix X with n>=p Bireduce reduce X to an upper bidiagola form The tranformations from the left are accumulmated in the np matrix U and the transformations from the right in the matrix V. on return X contains the genrators of the householder transformation used in the reduction X=U[d,e]V. More...

template<typename Matrix , typename Vector >
void	slip::Bi_complex_to_real (Vector &d, Vector &e, Matrix &U, Matrix &V)
	BiQR Given an upper bidiagonal matrix B, Bi_complex_to_real transforms the complex bidiagonal form into a real form. The tranformations from the left are accumulmated in the matrix U and the transformations from the right in the matrix V. More...

template<typename Matrix , typename Vector , typename Real , typename SizeType >
void	slip::BiQR (Vector &d, Vector &e, Real &sigma, const SizeType &row1, const SizeType &row2, Matrix &U, Matrix &V)
	BiQR Given an upper bidiagonal matrix B and a shift sigma, BiQR performs a QR step between rows row1 ans row2. The tranformations from the left are accumulmated in the matrix U and the transformations from the right in the matrix V. More...

template<typename Real >
void	slip::shift (Real &p, Real &r, Real &q, Real &sigma)
	Given a matrix $M = \left( \begin{array}{cc} p&r\\ 0&q\\ \end{array} \right)$ compute the smallest singular value of this matrix. More...

template<typename Vector , typename SizeType >
void	slip::BdBacksearch (Vector &d, Vector &e, const typename slip::lin_alg_traits< typename Vector::value_type >::value_type tol, SizeType &l, SizeType &i1, SizeType &i2)
	Back searching a bidiagonal Matrix this algorithm takes a bidiagobal matrix B, a tolerance tol and an index l(0<=l<=p-1) and determines indices i1,i2<=l such one of the following condictions holds 1) 0<=i1<i2<=l, in which case the matrix deflates as rows i1 and i2. 2) 0=i1=i2, in which case all the superdiagonal elements of B in rows 0 through l-1 are zero. More...

SVD Decomposition algorithms
template<typename Matrix1 , typename Matrix2 , typename RandomAccessIterator , typename Matrix3 >
void	slip::svd (const Matrix1 &M, Matrix2 &U, RandomAccessIterator S_first, RandomAccessIterator S_last, Matrix3 &V, const int max_it=75)
	(thin) Singular Value Decomposition Given a matrix M, this function computes its singular value decomposition, Any np matrix M whose number of rows n is greater than or equal to its number of columns p, can be written as the product of an np column-orthogonal matrix Up, an pp diagonal matrix S with positive or zero elements (the singular values), and the hermitian transpose of an pp orthogonal matrix V $M = \left( \begin{array}{ccc} u_{1,1}&\cdots&u_{1,p}\\ \vdots&&\vdots\\ u_{n,1}&\cdots&u_{n,p}\\ \end{array} \right) \left( \begin{array}{cccc} s_{1,1}&0&\cdots&0\\ 0&\ddots&\ddots&\vdots\\ \vdots&\ddots&\ddots&0\\ 0&\cdots&0&s_{p,p}\\ \end{array} \right) \left( \begin{array}{ccc} v_{1,1}&\cdots&v_{1,p}\\ \vdots&&\vdots\\ v_{p,1}&\cdots&v_{p,p}\\ \end{array} \right)^H$ More...

template<typename Matrix , typename Matrix2 >
void	slip::svd (const Matrix &X, Matrix &U, Matrix2 &S, Matrix &V, const int max_it=75)
	(thin) Singular Value Decomposition Given a matrix M, this function computes its singular value decomposition, Any np matrix M whose number of rows n is greater than or equal to its number of columns p, can be written as the product of an np column-orthogonal matrix Up, an pp diagonal matrix S with positive or zero elements (the singular values), and the transpose of an pp orthogonal matrix V $M = \left( \begin{array}{ccc} u_{1,1}&\cdots&u_{1,p}\\ \vdots&&\vdots\\ u_{n,1}&\cdots&u_{n,p}\\ \end{array} \right) \left( \begin{array}{cccc} s_{1,1}&0&\cdots&0\\ 0&\ddots&\ddots&\vdots\\ \vdots&\ddots&\ddots&0\\ 0&\cdots&0&s_{p,p}\\ \end{array} \right) \left( \begin{array}{ccc} v_{1,1}&\cdots&v_{1,p}\\ \vdots&&\vdots\\ v_{p,1}&\cdots&v_{p,p}\\ \end{array} \right)^H$ More...

SVD approximation algorithms
template<typename Matrix1 , typename RandomAccessIterator , typename Matrix2 , typename Matrix3 >
void	slip::svd_approx (const Matrix1 &U, RandomAccessIterator S_first, RandomAccessIterator S_last, const Matrix2 &V, const std::size_t K, Matrix3 &X)
	Singular Value Approximation of a matrix from its Singular Value Decomposition given by U, W and V: 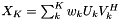$X_K = \sum_k^K w_k U_kV_k^H$ . More...

template<class Matrix1 , class Matrix2 , class Matrix3 , class Matrix4 >
void	slip::svd_approx (const Matrix1 &U, const Matrix2 &W, const Matrix3 &V, const std::size_t K, Matrix4 &M)
	Singular Value Approximation of a matrix from its Singular Value Decomposition given by U, W and V: 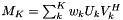$M_K = \sum_k^K w_k U_kV_k^H$ . More...

SVD system solve algorithms
template<class Matrix1 , typename RandomAccessIterator1 , class Matrix2 , typename RandomAccessIterator2 , typename RandomAccessIterator3 >
void	slip::svd_solve (const Matrix1 &U, RandomAccessIterator1 W_first, RandomAccessIterator1 W_last, const Matrix2 &V, RandomAccessIterator2 B_first, RandomAccessIterator2 B_last, RandomAccessIterator3 X_first, RandomAccessIterator3 X_last)
	Solve Linear (USV^H).X = B where U, S and V are provided by a svd decomposition. More...

template<class Matrix1 , typename RandomAccessIterator1 , typename RandomAccessIterator2 >
void	slip::svd_solve (const Matrix1 &A, RandomAccessIterator1 X_first, RandomAccessIterator1 X_last, RandomAccessIterator2 B_first, RandomAccessIterator2 B_last)
	Solve Linear Equation A.X = B using SVD decomposition. More...

template<class Matrix1 , class Vector1 , class Vector2 >
void	slip::svd_solve (const Matrix1 &A, Vector1 &X, const Vector2 &B)
	Solve Linear Equation A.X = B using SVD decomposition. More...

SVD inverse algorithms
template<class Matrix1 , typename RandomAccessIterator1 , class Matrix2 , class Matrix3 >
void	slip::svd_inv (const Matrix1 &U, RandomAccessIterator1 W_first, RandomAccessIterator1 W_last, const Matrix2 &V, Matrix3 &Ainv)
	Singular Value inverse of a matrix from its Singular Value Decomposition given by U, W and V. More...

template<class Matrix1 , class Matrix2 >
void	slip::svd_inv (const Matrix1 &A, Matrix2 &Ainv)
	Singular Value inverse of a matrix. More...

template<class Matrix1 , class Matrix2 >
void	slip::pinv (const Matrix1 &A, Matrix2 &Ainv)
	Pseudo inverse of a matrix. More...

Detailed Description

Provides some Singular Value Decomposition (SVD) algorithms.

Definition in file linear_algebra_svd.hpp.

Namespaces

Functions

Detailed Description