Provides some QR decomposition algorithms. More...

#include "linear_algebra.hpp"
#include "linear_algebra_traits.hpp"
#include "linear_algebra_svd.hpp"
#include "macros.hpp"
#include "gram_schmidt.hpp"
#include "compare.hpp"
#include <limits>
#include <vector>

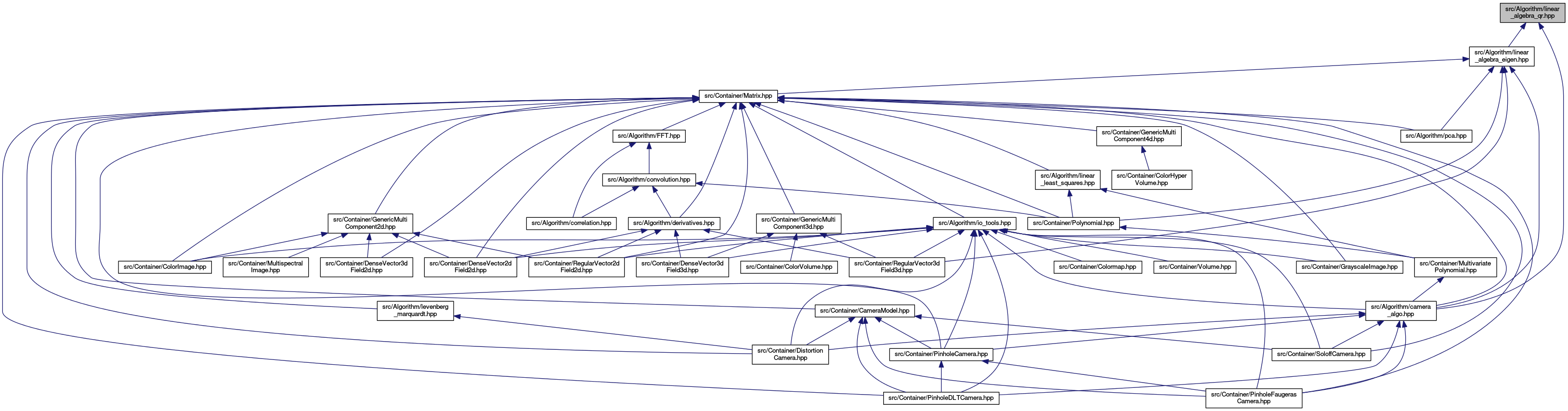
Include dependency graph for linear_algebra_qr.hpp:

This graph shows which files directly or indirectly include this file:

Go to the source code of this file.

Namespaces
	slip
	This namespace corresponds to the kernel of the Simple Library on Image Processing (SLIP). That is to say that it contains the data structures and the algorithms needed by these data strucutres.

Functions
template<class Matrix1 , class Matrix2 >
void	slip::balance (Matrix1 &A, Matrix2 &D)
	applies a diagonal similarity transform to the square matrix A to make the rows and columns as close in norm as possible. Balancing may reduce the 1-norm of the matrix, and improves the accuracy of the computed eigenvalues and/or eigenvectors. To avoid round-off errors, balance scales A with powers of 2. A is replaced by the balanced matrix which has the same eigenvalues and singular values : 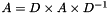$A = D \times A \times D^{-1}$ More...

template<typename MatrixIterator1 , typename MatrixIterator2 , typename MatrixIterator3 >
void	slip::gram_schmidt_qr (MatrixIterator1 A_up, MatrixIterator1 A_bot, MatrixIterator2 Q_up, MatrixIterator2 Q_bot, MatrixIterator3 R_up, MatrixIterator3 R_bot, const typename slip::lin_alg_traits< typename MatrixIterator1::value_type >::value_type tol)
	(modified) Gram-Schmidt qr decomposition. More...

template<typename Matrix1 , typename Matrix2 , typename Matrix3 >
void	slip::gram_schmidt_qr (const Matrix1 &A, Matrix2 &Q, Matrix3 &R, const typename slip::lin_alg_traits< typename Matrix1::value_type >::value_type tol)
	(modified) Gram-Schmidt qr decomposition. More...

template<typename Matrix1 , typename Vector >
void	slip::householder_qr (Matrix1 &M, Vector &V0)
	in place Householder QR decomposition M = QR $M = Q \times R$ $Q \times Q^{t} = I$ Q is a rotation matrix and R is an upper triangular matrix More...

template<typename Matrix1 , typename Matrix2 , typename Matrix3 >
void	slip::householder_qr (const Matrix1 &M, Matrix2 &Q, Matrix3 &R)
	Computes the QR decomposition of a matrix M : $M = Q \times R$ $Q \times Q^{t} = I$ Q is a rotation matrix and R is an upper triangular matrix. More...

template<typename MatrixIterator >
std::size_t	slip::subdiag_smaller_elem (MatrixIterator A_up, MatrixIterator A_bot, typename slip::lin_alg_traits< typename std::iterator_traits< MatrixIterator >::value_type >::value_type precision)
	find the smaller non null (according to the precision) subdiagonal element of a matrix More...

template<typename MatrixIterator1 , typename MatrixIterator2 , typename MatrixIterator3 >
void	slip::Schur_factorization_2by2 (MatrixIterator1 A_up, MatrixIterator1 A_bot, MatrixIterator2 Z_up, MatrixIterator2 Z_bot, MatrixIterator3 D_up, MatrixIterator3 D_bot)
	Computes the Schur factorization of a real 2-by-2 2d container : 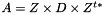$A = Z \times D \times Z^{t*}$ $\left( \begin{array}{cc} a & b \\ c & d \end{array}\right) = \left( \begin{array}{cc} cs & -sn \\ sn & cs \end{array}\right) \times \left( \begin{array}{cc} D_{00} & D_{01} \\ D_{10} & D_{11} \end{array}\right) \times \left( \begin{array}{cc} cs & sn \\ -sn & cs \end{array}\right)$ where : More...

template<class Matrix , typename VectorIterator >
void	slip::MatrixHouseholder (Matrix &H, VectorIterator V_begin, VectorIterator V_end)
	Computes the Householder matrix of a vector V : $H = I - \frac{2 \times V \times V^{t}}{V^{t} \times V}$ If V is an householder vector of a matrix M then $H \times M$ is a matrix with zeros on the first column (except the first element). More...

template<class Vector , typename MatrixIterator >
void	slip::VectorHouseholder (Vector &V, MatrixIterator M_up, MatrixIterator M_bot)
	Computes a Householder vector V from a matrix M : $V = M_{.0} - \alpha \times e_0$ with $M_{.0}$ represents the first column of M and $\alpha = - \frac{ M_{00}}{abs( M_{00})} \times \\|M_{.0}\\|$ . More...

template<typename HessenbergMatrix , typename Matrix >
bool	slip::Francis_QR_Step (HessenbergMatrix &H, Matrix &Z, slip::Box2d< int > box, bool compute_z)
	Computes the Francis QR Step used in the Schur decomposition $H = Z \times H \times Z^{t}$ Algorithm 7.5-1 in "Matrix Computations", Golub and Van Loan. More...

template<class HessenbergMatrix , class Vector , class Matrix >
void	slip::Francis_Schur_standardize (HessenbergMatrix &H, Vector &Eig, Matrix &Z, slip::Box2d< int > b22, bool compute_z)
	Converts a 2-by-2 diagonal block of H in the Schur form, normalizes H and extract the associated eigenvalues. $H = Z \times H \times Z^{t}$ Algorithm 7.5-1 in "Matrix Computations", Golub and Van Loan. More...

template<class HessenbergMatrix , class Vector , class Matrix >
bool	slip::Francis_Schur_decomp (HessenbergMatrix &H, Vector &Eig, Matrix &Z, slip::Box2d< int > &box, typename slip::lin_alg_traits< typename HessenbergMatrix::value_type >::value_type precision, bool compute_Z)
	computes the Schur decomposition of a square Hessenberg Matrix and copy the eigenvalues in the Eig vector : $H = Z \times H \times Z^{t}$ Algorithm 7.5-2 in "Matrix Computations", Golub and Van Loan. More...

template<class Matrix1 , class Matrix2 , class Vector , class Matrix3 >
bool	slip::schur (const Matrix1 &M, Matrix2 &H, Matrix3 &Z, Vector &Eig, bool compute_Z, typename slip::lin_alg_traits< typename Matrix1::value_type >::value_type precision=typename slip::lin_alg_traits< typename Matrix1::value_type >::value_type(1.0E-12))
	computes the shur decomposition of a square Matrix and copy the eigenvalues in the Eig vector: $M = Z \times H \times Z^{t}$ Algorithm 7.5-2 in "Matrix Computations", Golub and Van Loan. More...

template<class Matrix1 , class Matrix2 >
bool	slip::Sylvester_solve (const Matrix1 &S, slip::Box2d< int > &b11, slip::Box2d< int > &b22, double &g, Matrix2 &X)
	Solve the sylvester equation (from Z.Bai and J.W. Demmel article : -On Swapping Diagonal Blocks in Real Schur Form- In Linear Algebra and its Applications 186:73-95(1993)) : 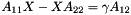$A_{11}X - XA_{22} = \gamma A_{12}$ . More...

Detailed Description

Provides some QR decomposition algorithms.

Definition in file linear_algebra_qr.hpp.

Namespaces

Functions

Detailed Description