Neighbors

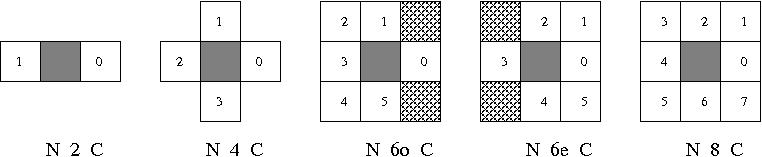
Some predefined neighborhood configurations

Some classical displacements around a current iterator are stored in static arrays. They are defined in the file neighbors.hpp . By the way, classical image processing neighborhood functors have been defined to get either a std::vector of the iterators (1d, 2d, 3d or 4d) of the neighbors of the current iterator (1d, 2d, 3d or 4d) either a std::vector of the values of the neighbors of the current iterator (1d, 2d, 3d or 4d). For each neighborhood configuration, a safe and an unsafe functor version are given. The safe version returns only existing neighbors. It permits to avoid the boring problem of image borders treatment. The unsafe version always returns the same number of neighbors. Consequently, it should be used with care. Nevertheless as no tests are done to verify that the neighbors are in the image are, computations should be faster than with safe functors. The main advantage of using functors is that you can write a same generic algorithm for various dimension and neighborhood configurations. You can even imagine to use the algorithm on a graph modeling your image on the condition to have defined a functor providing the neighbors of you current element on the graph. For that you have to follow the skeleton of the functors defined in neighborhood.hpp In the following, we give a description of these neighborhood configurations:

1d and 2d neighborhoods

Here are some functor to get the neighbors's iterators or values of a current iterator (1d or 2d).

• Safe 2-connexity neighbors functor
• Unsafe 2-connexity neighbors functor
• Safe 4-connexity neighbors functor
• Unsafe 4-connexity neighbors functor
• Safe 8-connexity neighbors functor
• Unsafe 8-connexity neighbors functor
• Safe pseudo-hexagonal neighbors functor
• Unsafe pseudo-hexagonal neighbors functor

3d neighborhood

Here are some functor to get the neighbors 3d iterators or values of a current 3d iterator:

6-connexity neighbors (slip::n_6c)

• Safe 6-connexity neighbors functor
• Unsafe 6-connexity neighbors functor

18-connexity neighbors (slip::n_18c)

• Safe 18-connexity neighbors functor
• Unsafe 18-connexity neighbors functor

26-connexity neighbors (slip::n_26c)

• Safe 26-connexity neighbors functor
• Unsafe 26-connexity neighbors functor

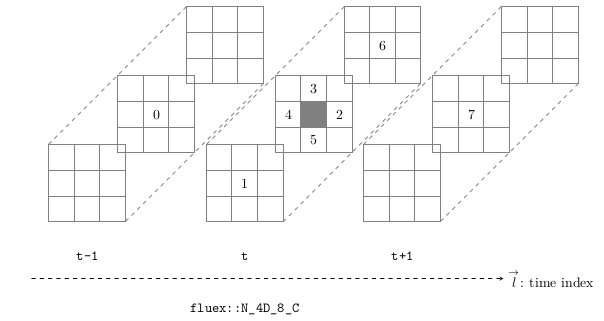
4d neighborhood

Here are some functor to get the neighbors 4d iterators or values of a current 4d iterator:

• Safe 4D 8-connexity neighbors functor
• Unsafe 4D 8-connexity neighbors functor

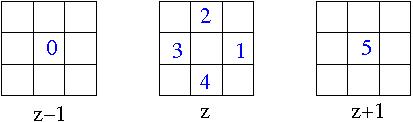
Some predefined successor and predecessor configuration

2d previous and next neighbors

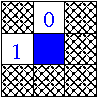
Previous 4-connexity

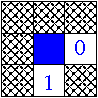
Next 4-connexity

• Safe 4-connexity previous neighbors
• Unsafe 4-connexity previous neighbors
• Safe 4-connexity next neighbors
• Unsafe 4-connexity next neighbors

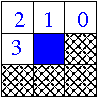
Previous 8-connexity

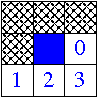
Next 8-connexity

• Safe 8-connexity previous neighbors
• Unsafe 8-connexity previous neighbors
• Safe 8-connexity next neighbors
• Unsafe 8-connexity next neighbors

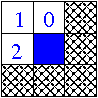
Previous odd pseudohexgonal

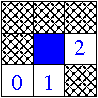
Next odd pseudohexgonal

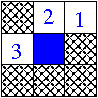
Previous even pseudohexgonal

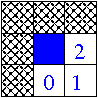
Next even pseudohexgonal

• Safe pseudohexagonal previous neighbors
• Unsafe pseudohexagonal previous neighbors
• Safe pseudohexagonal next neighbors
• Unsafe pseudohexagonal next neighbors

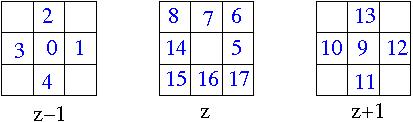
3d previous and next neighbors

• Safe 6-connexity previous neighbors
• Unsafe 6-connexity previous neighbors
• Safe 6-connexity next neighbors

• Unsafe 6-connexity next neighbors

• Safe 18-connexity previous neighbors
• Unsafe 18-connexity previous neighbors
• Safe 18-connexity next neighbors

• Unsafe 18-connexity next neighbors

• Safe 26-connexity previous neighbors
• Unsafe 26-connexity previous neighbors
• Safe 26-connexity next neighbors

• Unsafe 26-connexity next neighbors

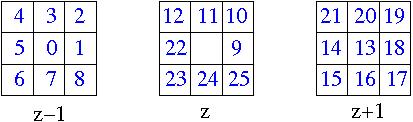
4d previous and next neighbors

• Safe 4D 8-connexity previous neighbors
• Unsafe 4D 8-connexity previous neighbors
• Safe 4D 8-connexity next neighbors
• Unsafe 4D 8-connexity next neighbors

Various ways to get neighbors

3x3 Median filtering using double loop and box

3x3 Median filtering unsing iterators and neighborhood functors

//median_filter function
template<typename Iterator1,
              typename Iterator2,
              typename NeighborFunc>
void median_filter_direct(Iterator1 in_first, Iterator1 in_last, 
                                    Iterator2 out_first, Iterator2 out_last,
                                    NeighborFunc N)
{
  typedef typename std::iterator_traits<Iterator1>::value_type value_type;
  //neighbors values vectors
  std::vector<value_type> neighbors(26);
 //iterate throw all elements
  for(; in_first != in_last; ++in_first, ++out_first)
   {
             //get neighborhoods of the current pixel: in_first
             N(in_first,neighbors);
     //add the current pixel
             neighbors.push_back(*in_first);
             //computes the median 
             *out_first = *slip::median(neighbors.begin(),neighbors.end());
    }
}

typedef double T;
   //---------------------------
   // Read the input image
   //---------------------------
   slip::GrayscaleImage<T> I;
   I.read(args[2]);
   const std::size_t rows = I.rows();
   const std::size_t cols = I.cols();
   //define the safe 8-connexity neighborhood functor
   //associated with I
   slip::SafeN8C<slip::GrayscaleImage<T> > Neigh(I);
   //----------------------------
   // Computes the median filter
   //----------------------------
   slip::GrayscaleImage<T> Median(rows,cols,0.0);
   median_filter_direct(I.upper_left(),I.bottom_right(),
                                                  Median.upper_left(),Median.bottom_right(),
                                                  Neigh);
    //---------------------------
   // Write the input image
   //---------------------------                                                  
   Median.write(args[4]);

typedef double T;
//---------------------------
// Read the input image
//---------------------------
slip::GrayscaleImage<T> I;
I.read(args[2]);
const std::size_t rows = I.rows();
const std::size_t cols = I.cols();
//------------------------------
// Enlarge input image
//------------------------------
slip::GrayscaleImage<T> Iborder;
const int bsize = 1;
slip::add_border2d(I,slip::BORDER_TREATMENT_COPY,Iborder,bsize);
Iborder.write("Iborder.png");
//define the unsafe 8-connexity neighborhood functor
slip::N8C Neigh;
//define the valid area of the enlarged image
    
slip::Box2d<int> box(bsize,bsize,(Iborder.rows()-1)-bsize,(Iborder.cols()-1)-bsize);
//----------------------------
// Computes the median filter
//----------------------------
slip::GrayscaleImage<T> Median(rows,cols,0.0);
median_filter_direct(Iborder.upper_left(box),Iborder.bottom_right(box),
                   Median.upper_left(),Median.bottom_right(),
                Neigh);

Median.write(args[4]);

Remarks

The same algorithm can obviously also been used on 1d, 3d or 4d containers

3x3 Median filtering unsing indirect iterators and neighborhood functors

template<typename Iterator1,
                typename Iterator2,
                typename NeighborFunc>
void median_filter_indirect(Iterator1 in_first, Iterator1 in_last, 
                                      Iterator2 out_first, Iterator2 out_last,
                                      NeighborFunc N)
{
  typedef typename std::iterator_traits<Iterator1>::value_type value_type;

  std::vector<Iterator1> neighbors(26);
  for(; in_first != in_last; ++in_first, ++out_first)
    {
             //get neighborhoods of the current pixel: in_first
             N(in_first,neighbors);
             //add current pixel
             neighbors.push_back(in_first);
             //definition of indirect_iterator to the neighbors
             boost::indirect_iterator<typename std::vector<Iterator1>::iterator,
                                      typename std::vector<value_type>::value_type>
               indirect_first(neighbors.begin()), 
               indirect_last(neighbors.end());
               assert(indirect_first != indirect_last);

               //get the median 
               *out_first = slip::median(indirect_first,indirect_last);
    }
}

typedef double T;
   //---------------------------
   // Read the input image
   //---------------------------
   slip::GrayscaleImage<T> I;
   I.read(args[2]);
   
   const std::size_t rows = I.rows();
   const std::size_t cols = I.cols();
   //define the safe 8-connexity neighborhood functor
   //associated with I
   slip::SafeN8C<slip::GrayscaleImage<T> > Neigh(I);

   //----------------------------
   // Computes the median filter
   //----------------------------
   slip::GrayscaleImage<T> Median(rows,cols,0.0);
   median_filter_indirect(I.upper_left(),I.bottom_right(),
                                                  Median.upper_left(),Median.bottom_right(),
                                                  Neigh);
   Median.write(args[4]);

3x3 Median filtering unsing iterators, neighborhood functors and a local median process functor

The local median process functor

struct median_func
{
 template <typename RandomAccessIterator>
 typename std::iterator_traits<RandomAccessIterator>::value_type 
operator()(RandomAccessIterator first, RandomAccessIterator last) const
{
  return slip::median(first,last);
}
};

The median algorithm

template<typename Iterator1,
              typename Iterator2,
              typename NeighborFunc,
              typename NeighborProcess>
void median_filter_direct(Iterator1 in_first, Iterator1 in_last, 
                                    Iterator2 out_first, Iterator2 out_last,
                                    NeighborFunc N,
                                    NeighborProcess NP)
{
  typedef typename std::iterator_traits<Iterator1>::value_type value_type;

  std::vector<value_type> neighbors(26);
  for(; in_first != in_last; ++in_first, ++out_first)
    {
             //get neighborhoods of the current pixel: in_first
             N(in_first,neighbors);
             neighbors.push_back(*in_first);
             //get the median 
             *out_first = NP(neighbors.begin(),neighbors.end());
    }
}

Call of the median algorithm

typedef double T;
    //---------------------------
    // Read the input image
    //---------------------------
    slip::GrayscaleImage<T> I;
    I.read(args[2]);
    
    const std::size_t rows = I.rows();
    const std::size_t cols = I.cols();
    //define the safe 8-connexity neighborhood functor
    //associated with I
    slip::SafeN8C<slip::GrayscaleImage<T> > Neigh(I);

    //----------------------------
    // Computes the median filter
    //----------------------------
    slip::GrayscaleImage<T> Median(rows,cols,0.0);
    //median_func LocalProcess;
    //min_func LocalProcess;
    max_func LocalProcess;
    //mean_func LocalProcess;
    median_filter_direct(I.upper_left(),I.bottom_right(),
                                                   Median.upper_left(),Median.bottom_right(),
                                                   Neigh,
                                   LocalProcess);
    Median.write(args[4]);