|
SLIP
1.4
|
All Classes Namespaces Files Functions Variables Typedefs Enumerations Enumerator Friends Macros Groups Pages
|
SLIP
1.4
|
Provides some polynomial algorithms. More...
#include "statistics.hpp"#include "Array2d.hpp"#include "arithmetic_op.hpp"#include <iterator>#include <iostream>#include <algorithm>#include <numeric>#include <cmath>
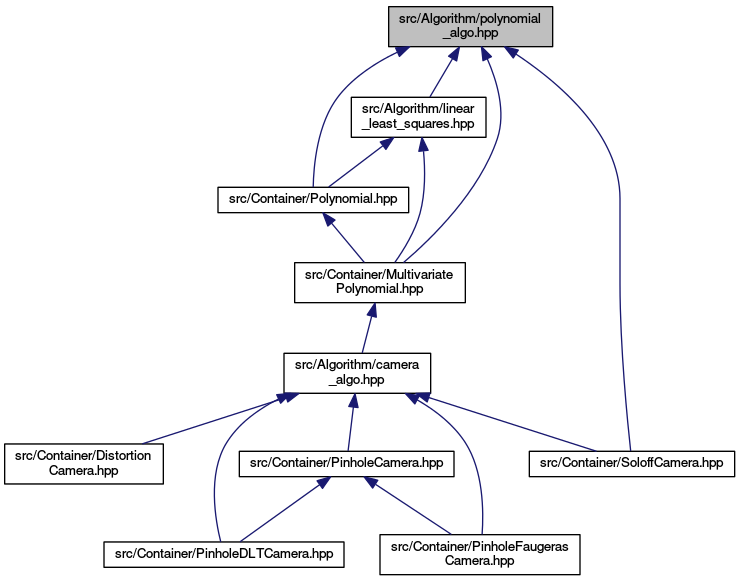
Go to the source code of this file.
Namespaces | |
| slip | |
| This namespace corresponds to the kernel of the Simple Library on Image Processing (SLIP). That is to say that it contains the data structures and the algorithms needed by these data strucutres. | |
Functions | |
Legendre polynomial algorithms | |
| template<typename Poly , typename Poly1 , typename Poly2 , typename Poly3 > | |
| Poly | slip::legendre_nd_next (std::size_t k, Poly1 x, Poly2 Pk, Poly3 Pkm1) |
| Implements the three term recurrence relation for the Legendre multivariate polynomials, this function can be used to create a sequence of orthogonal polynomial, and for rising k. This recurrence relation holds for Legendre Polynomials of both the first and second kinds:
. More... | |
| template<typename Poly , typename Poly1 , typename Poly2 , typename Poly3 > | |
| Poly | slip::legendre_next (std::size_t k, Poly1 x, Poly2 Pk, Poly3 Pkm1) |
| Implements the three term recurrence relation for the Legendre polynomials, this function can be used to create a sequence of orthogonal polynomial, and for rising k. This recurrence relation holds for Legendre Polynomials of both the first and second kinds:
. More... | |
Chebyshev polynomial algorithms | |
| template<typename Poly , typename Poly1 , typename Poly2 , typename Poly3 > | |
| Poly | slip::chebyshev_next (std::size_t k, Poly1 x, Poly2 Pk, Poly3 Pkm1) |
| Implements the three term recurrence relation for the Chebyshev polynomials, this function can be used to create a sequence of orthogonal polynomial, and for rising k. This recurrence relation holds for Chebyshev Polynomials of both the first and second kinds:
. More... | |
| template<typename Poly , typename Poly1 , typename Poly2 , typename Poly3 > | |
| Poly | slip::chebyshev_nd_next (std::size_t k, Poly1 x, Poly2 Pk, Poly3 Pkm1) |
| Implements the three term recurrence relation for the Chebyshev multivariate polynomials, this function can be used to create a sequence of orthogonal polynomial, and for rising k. This recurrence relation holds for Chebychev Polynomials of both the first and second kinds:
. More... | |
| template<typename T , typename RandomAccessIterator > | |
| void | slip::eval_chebyshevII_basis (const T &x, const std::size_t n, RandomAccessIterator first, RandomAccessIterator last) |
| Returns the evaluations of x until order n to the range [first,last) using the ChebyshevII scheme. The order of the resulting values is the following (1,2x,4x^2-1,8x^3-4x,...). More... | |
| template<typename T , typename RandomAccessIterator > | |
| void | slip::eval_discrete_chebyshev_basis (const T &x, const std::size_t n, RandomAccessIterator first, RandomAccessIterator last) |
| Returns the evaluations of x until order n to the range [first,last) using the Discrete Chebyshev scheme. The order of the resulting values is the following (1,2x-N+1,...). More... | |
Hermite polynomial algorithms | |
| template<typename Poly , typename Poly1 , typename Poly2 , typename Poly3 > | |
| Poly | slip::hermite_next (std::size_t k, Poly1 x, Poly2 Pk, Poly3 Pkm1) |
| Implements the three term recurrence relation for the Hermite polynomials, this function can be used to create a sequence of orthogonal polynomial, and for rising k. This recurrence relation holds for Hermite Polynomials:
. More... | |
| template<typename Poly , typename Poly1 , typename Poly2 , typename Poly3 > | |
| Poly | slip::hermite_nd_next (std::size_t k, Poly1 x, Poly2 Pk, Poly3 Pkm1) |
| Implements the three term recurrence relation for the Hermite multivariate polynomials, this function can be used to create a sequence of orthogonal polynomial, and for rising k. This recurrence relation holds for Hermite Polynomials:
. More... | |
| template<typename T , typename RandomAccessIterator > | |
| void | slip::eval_hermite_basis (const T &x, const std::size_t n, RandomAccessIterator first, RandomAccessIterator last) |
| Returns the evaluations of x until order n to the range [first,last) using the Hermite scheme. The order of the resulting values is the following (1,2x,4x^2-2,8x^3-12x,...). More... | |
Laguerre polynomial algorithms | |
| template<typename Poly , typename Poly1 , typename Poly2 , typename Poly3 > | |
| Poly | slip::laguerre_next (std::size_t k, Poly1 x, Poly2 Pk, Poly3 Pkm1) |
| Implements the three term recurrence relation for the Laguerre polynomials, this function can be used to create a sequence of orthogonal polynomial, and for rising k. This recurrence relation holds for Laguerre Polynomials:
. More... | |
| template<typename Poly , typename Poly1 , typename Poly2 , typename Poly3 > | |
| Poly | slip::laguerre_nd_next (std::size_t k, Poly1 x, Poly2 Pk, Poly3 Pkm1) |
| Implements the three term recurrence relation for the Laguerre multivariate polynomials, this function can be used to create a sequence of orthogonal polynomial, and for rising k. This recurrence relation holds for Laguere Polynomials:
. More... | |
| template<typename T , typename RandomAccessIterator > | |
| void | slip::eval_laguerre_basis (const T &x, const std::size_t n, RandomAccessIterator first, RandomAccessIterator last) |
| Returns the evaluations of x until order n to the range [first,last) using the Laguerre scheme. The order of the resulting values is the following (1,-x+1,0.5x^2-2x+1,-(1/6)x^3-(3/2)x^2-3x+1,...). More... | |
Polynome evaluation algorithms | |
| template<typename T , typename RandomAccessIterator > | |
| T | slip::eval_horner (RandomAccessIterator first, RandomAccessIterator last, const T &x) |
| Returns the evaluation of the polynomial given throw the range [first,last) at x using the horner scheme. The coefficients of the polynomial a0 + a1x + a2x^2 +... anx^n are supposed ordered as follows : (a0,a1,...,an). More... | |
| template<typename T , typename RandomAccessIterator > | |
| void | slip::eval_power_basis (const T &x, const std::size_t n, RandomAccessIterator first, RandomAccessIterator last) |
| Returns the evaluation of the power of x until order n to the range [first,last) using the horner scheme. More... | |
| template<typename T , typename RandomAccessIterator > | |
| void | slip::eval_legendre_basis (const T &x, const std::size_t n, RandomAccessIterator first, RandomAccessIterator last) |
| Returns the evaluations of x until order n to the range [first,last) using the legendre scheme. More... | |
| template<typename T , typename RandomAccessIterator > | |
| void | slip::eval_chebyshev_basis (const T &x, const std::size_t n, RandomAccessIterator first, RandomAccessIterator last) |
| Returns the evaluations of x until order n to the range [first,last) using the Chebyshev scheme. More... | |
| template<class Vector , typename RandomAccessIterator > | |
| void | slip::eval_power_2d_basis (const Vector &x, const std::size_t n, RandomAccessIterator first, RandomAccessIterator last) |
Returns the evaluation of the powers of X = (x1,x2) such that 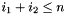 with with  and and  the power of x1 and x2. the range [first,last) using the horner scheme. More... the power of x1 and x2. the range [first,last) using the horner scheme. More... | |
| template<class Vector , typename RandomAccessIterator > | |
| void | slip::eval_power_nd_basis (const Vector &x, const std::size_t order, RandomAccessIterator first, RandomAccessIterator last) |
Returns the evaluation of the powers of 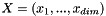 such that such that 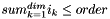 with with 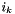 the power of the xk to the range [first,last) using the horner scheme. More... the power of the xk to the range [first,last) using the horner scheme. More... | |
| template<typename MultivariatePolynomial , typename RandomAccessIterator > | |
| void | slip::eval_multi_poly_power_basis (const MultivariatePolynomial &x, const std::size_t n, RandomAccessIterator first, RandomAccessIterator last) |
| Returns the evaluation of the power of a slip::MultivariatePolynomial<T,DIM> P until order n to the range [first,last) using the horner scheme. More... | |
| template<class Vector , typename RandomAccessIterator > | |
| void | slip::eval_multi_poly_power_nd_basis (const Vector &x, const std::size_t order, RandomAccessIterator first, RandomAccessIterator last) |
Returns the evaluation of the powers of slip::MultivariatePolynomial<T,DIM> 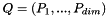 such that such that 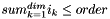 with with 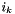 the power of the qk to the range [first,last) using the horner scheme. More... the power of the qk to the range [first,last) using the horner scheme. More... | |
Provides some polynomial algorithms.
Definition in file polynomial_algo.hpp.
 1.8.6
1.8.6